SYCL plugin¶
The SYCL plugin allows building interfaces that implement algorithms in SYCL.
Build¶
During the CMake configuration the flag ACTS_BUILD_PLUGIN_SYCL=on needs to be set. CMake will check whether our compiler is SYCL compatible and will look for available SYCL target architectures.
By default, SPIR 64-bits targets are looked for, but this can be configured with the SYCL_POSSIBLE_TARGETS variable.
For example, to target CUDA backends, we should set this variable to nvptx64-nvidia-cuda-sycldevice.
Also, by setting the variable SYCL_SEARCH_SUPPORT_LIBRARIES it is possible to specify support libraries or object files that are needed for execution on a specific target. Missing object files cause a runtime error.
Device selection¶
Firstly, we can list available platforms and devices with clinfo:
[bash][atspot01]:build > clinfo
Number of platforms 3
Platform Name Intel(R) OpenCL
Platform Vendor Intel(R) Corporation
Platform Version OpenCL 2.1 LINUX
...
CMake should recognize these platforms during configuration (if not told otherwise).
There are more options we can choose from to configure device selection (meaning constructing a cl::sycl::device_selector object).
We can alter the behavior of the SYCL default_selector by setting the environment variable SYCL_BE (BE stands for backend).
For example by setting it to PI_CUDA it forces the usage of the CUDA backend (if available).
Similarly PI_OPENCL forces the usage of the OpenCL backend. For more information see this Getting Started guide.:
SYCL_BE=PI_CUDA <binary> <arguments>
We can also use a custom device selector. As an example, see Acts::Sycl::DeviceSelector, which selects a non-OpenCL CUDA backend.
This is the device selector used by the Acts::Sycl::QueueWrapper object that manages the construction, ownership and destruction of a cl::sycl::queue object.
This solution allows us to construct a queue object in translation units that are not linked against SYCL.
SYCL Seeding¶
Usage¶
To create a Seedfinder object that implements the seeding algorithm in SYCL, we need to instantiate an object from Acts::Sycl::Seedfinder.
Similarly to Acts::Seedfinder, we need to provide a configuration object of Acts::SeedfinderConfig and an object that implements experiment specific cuts.
As these cuts are performed in SYCL kernels (on the device side), instead of a IExperimentCuts instance, we need to construct a DeviceExperimentCuts one.
Seedfinder(
Acts::SeedfinderConfig<external_spacepoint_t> config,
const Acts::Sycl::DeviceExperimentCuts& cuts,
Acts::Sycl::QueueWrapper wrappedQueue = Acts::Sycl::QueueWrapper());
In the current implementation, the member functions DeviceExperimentCuts::seedWeight() and DeviceExperimentCuts::singleSeedCut() in the header file DeviceExperimentCuts.hpp need to be rewritten to have our custom experiment cuts.
float seedWeight(const detail::DeviceSpacePoint& bottom,
const detail::DeviceSpacePoint& middle,
const detail::DeviceSpacePoint& top) const {...}
/*...*/
bool singleSeedCut(float weight, const detail::DeviceSpacePoint& bottom,
const detail::DeviceSpacePoint& middle,
const detail::DeviceSpacePoint& top) const {...}
Optionally we can also give a Acts::Sycl::QueueWrapper object to the constructor of Acts::Sycl::Seedfinder, which is a wrapper object around a cl::sycl::queue type.
This allows us to construct our own queue instance and to reuse it.
Implementation details¶
The following section describes memory management, kernel scheduling and array indexing for the SYCL seed finding algorithm.
We start out with the duplet search that looks for compatible bottom-middle and middle-top space point pairs.
In case we have 5 middle SP and 4 bottom SP, our temporary array of the compatible bottom duplet indices would look like this:
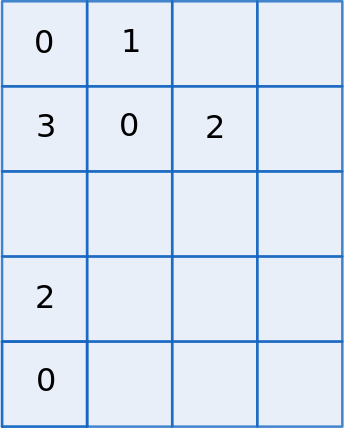
Fig. 6 Rows correspond to middle space points, numbers are bottom space point indices. Threads are executed concurrently, so the order of bottom SP indices is random.¶
We will flatten this matrix out, and store the indices the following way:

Fig. 7 Storing bottom SP indices for all middle SPs.¶
To be able to get the indices of middle SPs in constant time inside kernels, we will also prepare arrays that store the indices of the middleSPs of the edges.
(For the same purpose, we could also do a binary search on the array on Fig. 8, and we will do exactly that later, in the triplet search kernel.)
To find out where the indices of bottom SPs start for a particular middle SP, we use prefix sum arrays. We know how many duplets were found for each middle SP:
We will make a prefix sum array of these counts, with a leading zero:

Fig. 8 Prefix sum array of the counted values of compatible bottom SPs per middle SP.¶
If we have the middle SP with index 1, then we know that the indices of the compatible bottom SPs are in the range (left closed, right open) [2,5) of the previously flattened array in Fig. 7. In this case, these indices are 3 and 2, so we’d use these to index deviceBottomSPs to gather data about the bottom SP.
In this example, will execute the coordinate transformation on 7 threads.
The size of the array storing our transformed coordinates is also 7, the sum of bottom duplets we found so far.
The process for middle-top space points is the same.
For the triplet search, we calculate the upper limit of constructible triplets.
For this, we multiply the number of compatible bottom and compatible top SPs for each middle SP, and add these together. This is \(nb_0*nt_0 + nb_1*nt_1 + ...\) where \(nb_k\) is the number of compatible bottom SPs for the \(k\) is for tops.
We construct a prefix sum array (of length \(M+1\)) of the calculated combinations. (Where \(M\) is the number of middle space points.)
middle SPs |
\(middleSP_0\) |
\(middleSP_1\) |
… |
\(middleSP_M\) |
|---|---|---|---|---|
number of combinations |
\(nb_0*nt_0\) |
\(nb_0*nt_0 + nb_1*nt_1\) |
… |
\(\sum_{i=0}^{M}nb_i*nt_i\) |
We will start kernels and reserve memory for these combinations but only so much we can fit into memory at once.
For later, let \(MAM\) be the maximum allocatable memory for triplet search.
We start by adding up summing the combinations, until we arrive at a \(k\) which for:
(or \(k = M\)).
So we know, that we need to start our first kernel for the first \(k\) middle SPs.
Inside the triplet search kernel we start with a binary search, to find out which middle SP the thread corresponds to. Note, that the array in table-1 is a monotone increasing series of values which allows us to do a binary search on it.
Inside the triplet search kernel we count the triplets for fixed bottom and middle SP.
The triplet filter kernel is calculated on threads equal to all possible bottom-middle combinations for the first \(k\) middle SPs, which are the sum of bottom-middle duplets.
If the triplet search and triplet filter kernel finished, we continue summing up possible triplet combinations from the \((k+1)\) th middle SP.
Inside the kernels we need to use an offset, to be able to map threads to space point indices.
Performance¶
It depends on our architecture, the size of the event we are reconstructing, and the effectiveness of our experiment specific cuts how well the algorithm performs, and whether we can benefit at all from using the SYCL plugin. It is advised to compare performance and precision first with the CPU version of the chosen algorithm. This should be possible with the tests provided.
Resources¶
For more information about SYCL see the specification (date: 2020. September 7.). There is a documentation for Intel implementation and DPC++ extensions (see examples).

