Magnetic field¶
Attention
This section is largely outdated and will be replaced in the future.
This module collects information about classes and typedefs useful for
describing different magnetic field configurations. Acts is independent of the
magnetic field implementation used. Algorithms which need magnetic field
information (e.g. Acts::AtlasStepper,
Acts::EigenStepper) are templated on the magnetic field. The
requirements for the magnetic field implementation are shown in the example FieldProvider given below:
struct FieldProvider {
struct Cache {
// implementation specific
};
// get field for a given position, no cache
Vector3 getField(const Vector3& pos) const;
// get field and the gradient, no cache
Vector3 getFieldGradient(const Vector3& pos, ActsMatrix<3,3>& deriv) const;
// get the field for a given position, and provide the cache object
Vector3 getField(const Vector3& position, Cache& cache) const;
// get the field and gradient for a given position, provide cache
Vector3 getFieldGradient(const Vector3& pos,
ActsMatrix<3,3>& deriv, // mutable reference
Cache& cache) const;
};
// client code
FieldProvider p;
FieldProvider::Cache cache;
auto field = p.getField({1, 2, 3}, cache); // retrieve field
Each magnetic field implementation expects to be passed a reference to an
implementation specific cache object. The cache type is provided as a nested
struct of the field provider. It can usually be extracted using typename BField::Cache cache, where BField is a template parameter. Acts comes
with the following implementations of this (implicit) interface:
Constant magnetic field¶
The simplest implementation is a constant field, which returns the same field values at every queried location. It is implemented in the Acts::ConstantBField class.
-
class ConstantBField : public Acts::MagneticFieldProvider
This class implements a simple constant magnetic field.
The magnetic field value has to be set at creation time, but can be updated later on.
Public Functions
-
inline explicit ConstantBField(Vector3 B)
Construct constant magnetic field from field vector.
- Parameters
B – [in] magnetic field vector in global coordinate system
-
inline explicit ConstantBField(Vector3 B)
As seen above, the class is constructed from a three-dimensional field vector, which is returned unmodified to every call to Acts::ConstantBField::getField().
Interpolated magnetic field¶
For more complex magnetic field implementations the
Acts::InterpolatedBFieldMap can be used. The idea here is to calculate
an interpolated value of the magnetic field from a grid of known field values.
In 3D, this means the interpolation is done from the 8 cornerpoints of a field
cell. The field cell can be retrieved for any given position. Since during
typical access patterns, e.g. the propagation, subsequent steps are relatively
likely to not cross the field cell boundary, the field cell can be cached.
Fig. 1 Illustration of the field cell concept. Subsequent steps are clustered in the same field cell. The field cell only needs to be refetched when the propagation crosses into the next grid region.¶
The class constructor
-
inline Acts::InterpolatedBFieldMap::InterpolatedBFieldMap(Config cfg)¶
accepts a single object of type Acts::InterpolatedBFieldMap::Config:
-
struct Config
Public Members
-
double scale = 1.
-
double scale = 1.
The config object contains an instance of a mapper type, as well as a global scale to be applied to any field values.
One implementation Acts::InterpolatedBFieldMapper is provided, but
since the mapper type is a template parameter, this implementation can also be
switched out. The default implementation uses Acts::detail::Grid as
the underlying data storage. It is generic over the number of dimensions.
Most notably it exposes a type
Acts::InterpolatedBFieldMapper::FieldCell that corresponds to the
concept of a field cell discussed above. It also exposes a function
that allows the retrieval of such a field cell at a given position. This function
is used by Acts::InterpolatedBFieldMap to lookup and use field cells.
Acts::InterpolatedBFieldMap stores the most recent field cell in
the Cache object provided by the client, and only talk to
Acts::InterpolatedBFieldMapper when the position leaves the current
field cell. Access to the magnetic field is done using the common interface methods
-
template<typename grid_t>
class InterpolatedBFieldMap : public Acts::InterpolatedMagneticField
where the Cache type hides the concrete mapper used.
Helpers to construct mappers from text and root file inputs are provided:
Acts::fieldMapperRZ()Acts::fieldMapperXYZ()
Analytical solenoid magnetic field¶
Acts also provides a field provider that calculates the field vectors analytically for a solenoid field.
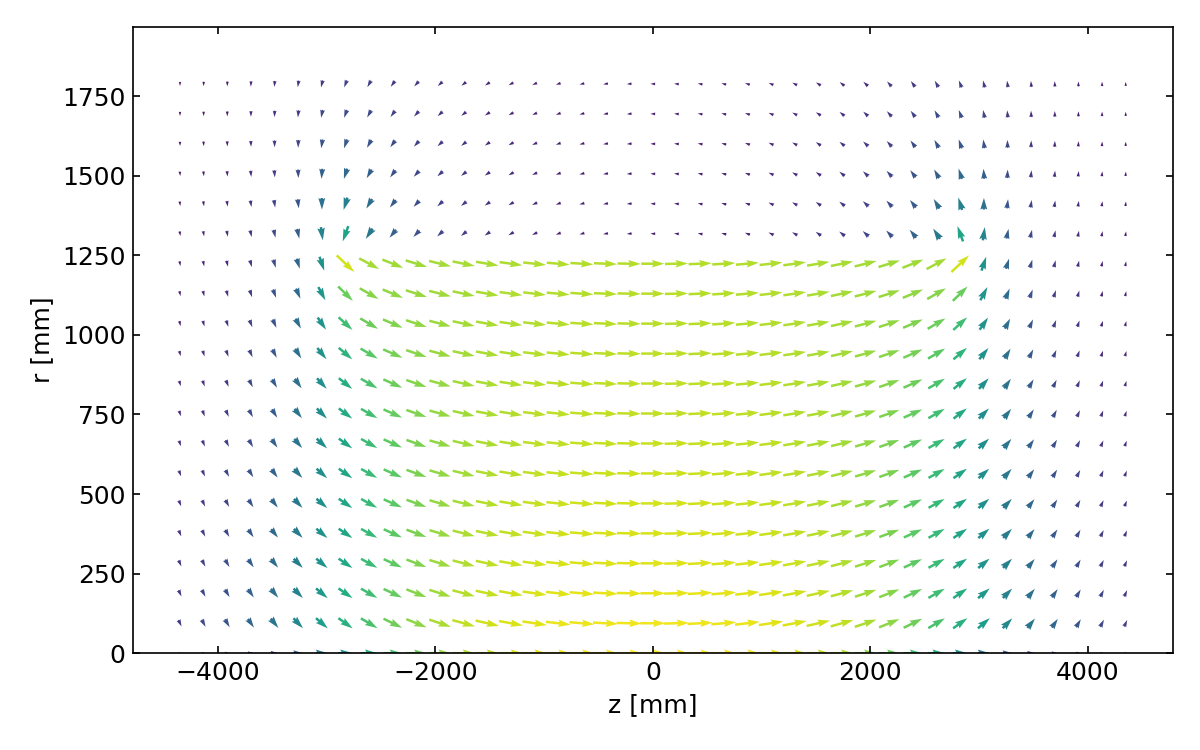
The implementation has configurable solenoid parameters:
-
struct Config
Config struct for the SolenoidBfield.
Public Members
-
double bMagCenter
The target magnetic field strength at the center.
This will be used to scale coefficients
-
double length
Extent of the solenoid in z.
It goes from -length/2 to +length/2 by convention
-
size_t nCoils
The number of coils that make up the solenoid.
-
double radius
Radius at which the coils are located.
-
double bMagCenter
Note
A configuration of
SolenoidBField::Config cfg;
cfg.length = 5.8_m;
cfg.radius = (2.56 + 2.46) * 0.5 * 0.5_m;
cfg.nCoils = 1154;
cfg.bMagCenter = 2_T;
SolenoidBField bField(cfg);
roughly corresponds to the solenoid wrapping the Inner Detector in ATLAS.
Implementation¶
The calculation uses two special functions:
\(E_1(k^2)\) is the complete elliptic integral of the 1st kind
\(E_2(k^2)\) is the complete elliptic integral of the 2nd kind
\(E_1(k^2)\) and \(E_2(k^2)\) are usually indicated as \(K(k^2)\) and \(E(k^2)\) in literature, respectively:
\(k^2\) is a function of the point \((r, z)\) and of the radius of the coil \(R\)
Using these, you can evaluate the two components \(B_r\) and \(B_z\) of the magnetic field:
In the implementation the factor of \((\mu_0\cdot I)\) is defined to be a scaling factor. It is evaluated and defined as the magnetic field in the center of the coil, i.e. the scale set in Acts::SolenoidBField::Config::bMagCenter.
Warning
Evaluation of \(E_1(k^2)\) and \(E_2(k^2)\) is slow. The
Acts::InterpolatedBFieldMap easily outperforms
Acts::SolenoidBField. A helper Acts::solenoidFieldMapper()
is provided that builds a map from the analytical implementation and is
much faster to lookup.