Geometry module¶

The ACTS geometry model is strongly based on the ATLAS Tracking geometry. Its core is built on a surface-based description that make up all geometry objects of higher complexity. This design has been chosen as the surface objects can be used together with the track propagation module and thus all geometry objects become natively integrated into the tracking software.

Note

There is an ongoing rewrite of the geometry and navigation modules where logical layers will be modelled as volumes, see Experimental Geometry module.

GeometryObject base class¶

All geometry objects in Acts inherit from a virtual Acts::GeometryObject base class.

class GeometryObject

Base class to provide GeometryIdentifier interface:

simple set and get

It also provides the binningPosition method for Geometry geometrical object to be binned in BinnedArrays

Subclassed by Acts::Layer, Acts::Surface, Acts::Volume

Public Functions

GeometryObject() = default: Defaulted constructor.

GeometryObject(const GeometryObject&) = default: Defaulted copy constructor.

inline GeometryObject(const GeometryIdentifier &geometryId)

Constructor from a value.

Parameters: geometryId – the geometry identifier of the object

inline void assignGeometryId(const GeometryIdentifier &geometryId)

Set the value.

Parameters: geometryId – the geometry identifier to be assigned

virtual Vector3 binningPosition(const GeometryContext &gctx, BinningValue bValue) const = 0

Force a binning position method.

Parameters

gctx – The current geometry context object, e.g. alignment
bValue – is the value in which you want to bin

Returns

vector 3D used for the binning schema

inline virtual double binningPositionValue(const GeometryContext &gctx, BinningValue bValue) const

Implement the binningValue.

Parameters

gctx – The current geometry context object, e.g. alignment
bValue – is the dobule in which you want to bin

Returns

float to be used for the binning schema

inline const GeometryIdentifier &geometryId() const

Returns: the geometry id by reference

inline GeometryObject &operator=(const GeometryObject &geometryId)

Assignment operator.

Parameters: geometryId – the source geometryId

Note

The binningPosition(const GeometryContext& gctx, BinningValue& bVal) method allows to define a customized position of this object when being subject to ordering in some specific binnings, e.g. in a BinnedArray or a SurfaceArray.

This class ensures that a unique Acts::GeometryIdentifier is assigned to every geometry object.

Geometry identifier¶

The Acts::GeometryIdentifier is mainly used for fast identification of the type of the geometry object (as most of them are either extensions or containers of the Acts::Surface objects) and for the identification of the geometry surfaces after building, e.g. for the uploading/assigning of material to the surface after creation. The Acts::GeometryIdentifier uses a simple masking procedure for applying an identification schema.

While it is used in Acts-internal applications such as material mapping, it is not employed for EventData and Geometry identification in an experiment setup. Instead, one should define and use the Identifier class in the latter case.

class GeometryIdentifier

Identifier for geometry nodes within the geometry hierarchy.

An identifier can be split into the following components. They define a hierarchy of objects starting from the high-level volumes:

Volume
Boundary surfaces (for a volume)
Layers (confined within a volume)
Approach surfaces (for a layer)
Sensitive surfaces (confined to a layer, also called modules)

Private Static Attributes

static constexpr Value kApproachMask = 0x0000000ff0000000: (2^8)-1 = 255 approach surfaces

static constexpr Value kBoundaryMask = 0x00ff000000000000: (2^8)-1 = 255 boundaries

static constexpr Value kExtraMask = 0x00000000000000ff: (2^8)-1 = 255 extra values

static constexpr Value kLayerMask = 0x0000fff000000000: (2^12)-1 = 4095 layers

static constexpr Value kSensitiveMask = 0x000000000fffff00: (2^20)-1 = 1048575 sensitive surfaces

static constexpr Value kVolumeMask = 0xff00000000000000: (2^8)-1 = 255 volumes

Surface classes¶

All classes which represent a thin surface in ACTS inherit from the common virtual base class Acts::Surface, which defines the public interface of all surfaces. While the different concrete surface classes are defined by their respective native local coordinate system, the shapes on these surfaces are defined by classes that inherit from Acts::SurfaceBounds, which every surface must provide. In case of boundless surfaces, a special Acts::InfiniteBounds class is available.

Each Acts::Surface instance reports its type from Acts::Surface::type():

enum Acts::Surface::SurfaceType

This enumerator simplifies the persistency & calculations, by saving a dynamic_cast, e.g.

for persistency

Values:

enumerator Cone

enumerator Cylinder

enumerator Disc

enumerator Perigee

enumerator Plane

enumerator Straw

enumerator Curvilinear

enumerator Other

Surface Type	Local Coordinates	Bound Types available
`Acts::ConeSurface`	\([r\phi, z]\)	`Acts::ConeBounds`
`Acts::CylinderSurface`	\([r, \phi]\)	`Acts::CylinderBounds`
`Acts::DiscSurface`	\([r, \phi]\)	`Acts::RadialBounds`, `Acts::DiscTrapezoidalBounds`
`Acts::PlaneSurface`	\([x, y]\)	`Acts::RectangleBounds`, `Acts::TrapezoidalBounds`, `Acts::TriangleBounds`,`Acts::InfiniteBounds`, `Acts::EllipseBounds`
`Acts::PerigeeSurface`, `Acts::StrawSurface`	\([d, z]\)	`Acts::CylinderBounds`
`Acts::LineSurface`	\([d_0, z_0]\)	`Acts::LineBounds`

Tip

In an ideal setup, the coordinate systems also define the readout measurement directions. In such a case, a track prediction from the propagation will already be in the correct frame of the measurement and residual or compatibility checks will not need additional coordinate transformations.

Plane surface¶

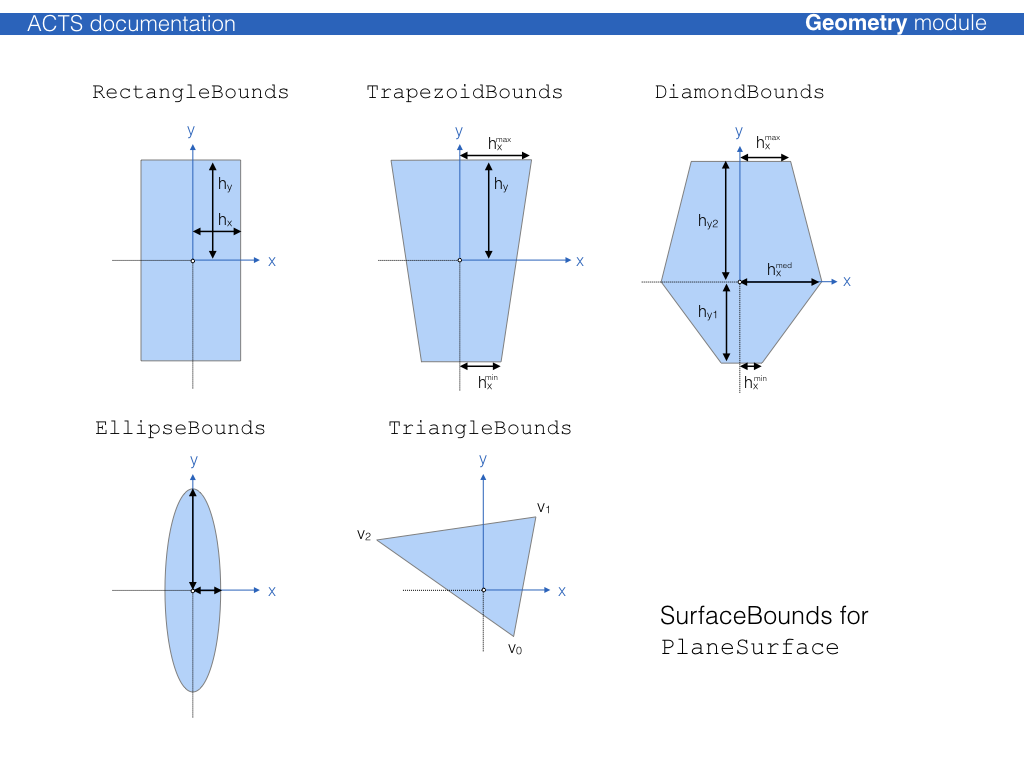
PlaneBounds

class PlaneSurface : public Acts::Surface

Class for a planaer in the TrackingGeometry.

The PlaneSurface extends the Surface class with the possibility to convert local to global positions (vice versa).

_build/doxygen-xml/PlaneSurface.png

Subclassed by Acts::PlaneLayer

Public Functions

virtual Result<Vector2> globalToLocal(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, double tolerance = s_onSurfaceTolerance) const override

Global to local transformation.

Note

For planar surfaces the momentum direction is ignored in the global to local transformation

Parameters

gctx – The current geometry context object, e.g. alignment
position – global 3D position - considered to be on surface but not inside bounds (check is done)
direction – global 3D momentum direction (optionally ignored) method symmetry)
tolerance – optional tolerance within which a point is considered valid on surface

Returns

a Result<Vector2> which can be !ok() if the operation fails

virtual SurfaceIntersection intersect(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck = false, ActsScalar tolerance = s_onSurfaceTolerance) const final

Straight line intersection.

mathematical motivation:

the equation of the plane is given by: \( \vec n \cdot \vec x = \vec n \cdot \vec p,\) where \( \vec n = (n_{x}, n_{y}, n_{z})\) denotes the normal vector of the plane, \( \vec p = (p_{x}, p_{y}, p_{z})\) one specific point on the plane and \( \vec x = (x,y,z) \) all possible points on the plane.

Given a line with:\( \vec l(u) = \vec l_{1} + u \cdot \vec v \)

,

the solution for

\( u \) can be written: \( u = \frac{\vec n (\vec p - \vec l_{1})}{\vec n \vec v}\) If the denominator is 0 then the line lies:

either in the plane
perpendicular to the normal of the plane

Note

expected to be normalized)

Parameters

gctx – The current geometry context object, e.g. alignment
position – The start position of the intersection attempt
direction – The direction of the intersection attempt, (
bcheck – The boundary check directive
tolerance – the tolerance used for the intersection

Returns

the SurfaceIntersection object

virtual Vector3 localToGlobal(const GeometryContext &gctx, const Vector2 &lposition, const Vector3 &direction) const override

Local to global transformation.

Note

For planar surfaces the momentum direction is ignored in the local to global transformation

Parameters

gctx – The current geometry context object, e.g. alignment
lposition – local 2D position in specialized surface frame
direction – global 3D momentum direction (optionally ignored)

Returns

the global position by value

virtual Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const final

Normal vector return.

return a Vector3 by value

Parameters

gctx – The current geometry context object, e.g. alignment
lposition – is the local position is ignored

Disc surface¶

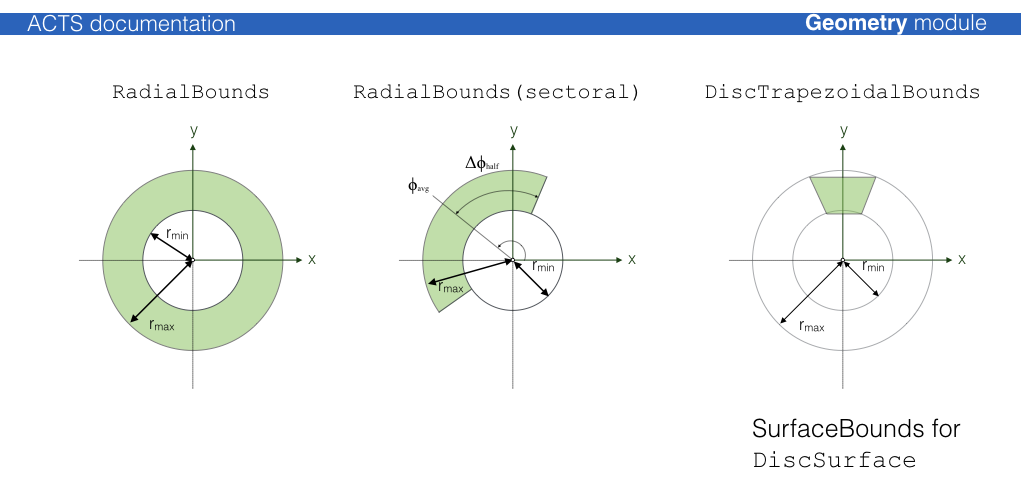
DiscBounds

class DiscSurface : public Acts::Surface

Class for a disc surface (or a segment thereof)

The DiscSurface is defined by the local polar coordinates \( (r,phi) \).

The surface transform positions the disc such that the origin is at \( r=0 \), independent of the provided DiscBounds. The normal vector of the disc (i.e., the local \(z\)-axis) is given by \( \vec e_{z} = \vec e_{r} \times\vec e_{phi} \).

The disc surface The only surface type for which the covariance matrix is NOT given in the reference frame. A conversion from polar to cartesian coordinates needs to happen to transfer the local coordinates onto the cartesian reference frame coordinates.

_build/doxygen-xml/DiscSurface.png

Subclassed by Acts::DiscLayer

Public Functions

virtual Result<Vector2> globalToLocal(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, double tolerance = s_onSurfaceTolerance) const final

Global to local transformation.

Note

the direction is ignored for Disc surfaces in this calculateion

Parameters

gctx – The current geometry context object, e.g. alignment
position – global 3D position - considered to be on surface but not inside bounds (check is done)
direction – global 3D momentum direction (optionally ignored)
tolerance – optional tolerance within which a point is considered valid on surface

Returns

a Result<Vector2> which can be !ok() if the operation fails

virtual SurfaceIntersection intersect(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck = false, ActsScalar tolerance = s_onSurfaceTolerance) const final

Straight line intersection schema.

Mathematical motivation:

the equation of the plane is given by: \( \vec n \cdot \vec x = \vec n \cdot \vec p,\) where \( \vec n = (n_{x}, n_{y}, n_{z})\) denotes the normal vector of the plane, \( \vec p = (p_{x}, p_{y}, p_{z})\) one specific point on the plane and \( \vec x = (x,y,z) \)

all possible points on the plane.

Given a line with:

\( \vec l(u) = \vec l_{1} + u \cdot \vec v \)

,

the solution for

\( u \) can be written: \( u = \frac{\vec n (\vec p - \vec l_{1})}{\vec n \vec v}\) If the denominator is 0 then the line lies:

either in the plane
perpendicular to the normal of the plane

Note

expected to be normalized (no checking)

Parameters

gctx – The current geometry context object, e.g. alignment
position – The global position as a starting point
direction – The global direction at the starting point
bcheck – The boundary check prescription
tolerance – the tolerance used for the intersection

Returns

The SurfaceIntersection object

virtual Vector3 localToGlobal(const GeometryContext &gctx, const Vector2 &lposition, const Vector3 &direction) const final

Local to global transformation For planar surfaces the momentum direction is ignored in the local to global transformation.

Parameters

gctx – The current geometry context object, e.g. alignment
lposition – local 2D position in specialized surface frame
direction – global 3D momentum direction (optionally ignored)

Returns

global position by value

virtual Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const final

Normal vector return.

Parameters

gctx – The current geometry context object, e.g. alignment
lposition – The local position is ignored

Returns

a Vector3 by value

Cylinder surface¶

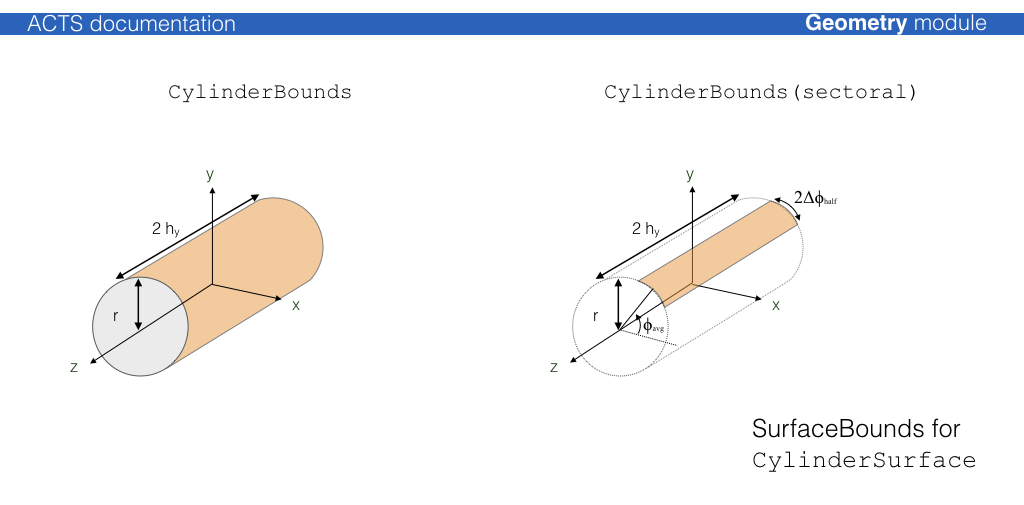
CylinderBounds

class CylinderSurface : public Acts::Surface

Class for a CylinderSurface in the TrackingGeometry.

It inherits from Surface.

The cylinder surface has a special role in the TrackingGeometry, since it builds the surfaces of all TrackingVolumes at container level for a cylindrical tracking geometry.

_build/doxygen-xml/CylinderSurface.png

Subclassed by Acts::CylinderLayer

Public Functions

virtual Result<Vector2> globalToLocal(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, double tolerance = s_onSurfaceTolerance) const final

Global to local transformation.

Parameters

gctx – The current geometry context object, e.g. alignment
position – is the global position to be transformed
direction – is the global momentum direction (ignored in this operation)
tolerance – optional tolerance within which a point is considered valid on surface

Returns

a Result<Vector2> which can be !ok() if the operation fails

virtual SurfaceIntersection intersect(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck = false, ActsScalar tolerance = s_onSurfaceTolerance) const final

Straight line intersection schema from position/direction.

If possible returns both solutions for the cylinder

Parameters

gctx – The current geometry context object, e.g. alignment
position – The position to start from
direction – The direction at start
bcheck – the Boundary Check
tolerance – the tolerance used for the intersection

Returns

SurfaceIntersection object (contains intersection & surface)

virtual Vector3 localToGlobal(const GeometryContext &gctx, const Vector2 &lposition, const Vector3 &direction) const final

Local to global transformation.

Parameters

gctx – The current geometry context object, e.g. alignment
lposition – is the local position to be transformed
direction – is the global momentum direction (ignored in this operation)

Returns

The global position by value

virtual Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const final

Return method for surface normal information.

Note

for a Cylinder a local position is always required for the normal vector

Parameters

gctx – The current geometry context object, e.g. alignment
lposition – is the local position for which the normal vector is requested

Returns

normal vector at the local position by value

virtual Vector3 normal(const GeometryContext &gctx, const Vector3 &position) const final

Return method for surface normal information.

Note

for a Cylinder a local position is always required for the normal vector

Parameters

gctx – The current geometry context object, e.g. alignment
position – is the global position for which the normal vector is requested

Returns

normal vector at the global position by value

Cone surface¶

class ConeSurface : public Acts::Surface

Class for a conical surface in the Tracking geometry.

It inherits from Surface.

The ConeSurface is special since no corresponding Track parameters exist since they’re numerical instable at the tip of the cone. Propagations to a cone surface will be returned in curvilinear coordinates.

Subclassed by Acts::ConeLayer

Public Functions

virtual Result<Vector2> globalToLocal(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, double tolerance = s_onSurfaceTolerance) const final

Global to local transformation.

Parameters

gctx – The current geometry context object, e.g. alignment
position – is the global position to be transformed
direction – is the global momentum direction (ignored in this operation)
tolerance – optional tolerance within which a point is considered valid on surface

Returns

a Result<Vector2> which can be !ok() if the operation fails

virtual SurfaceIntersection intersect(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck = false, double tolerance = s_onSurfaceTolerance) const final

Straight line intersection schema from position/direction.

If possible returns both solutions for the cylinder

Parameters

gctx – The current geometry context object, e.g. alignment
position – The position to start from
direction – The direction at start
bcheck – the Boundary Check
tolerance – the tolerance used for the intersection

Returns

SurfaceIntersection object (contains intersection & surface)

virtual Vector3 localToGlobal(const GeometryContext &gctx, const Vector2 &lposition, const Vector3 &direction) const final

Local to global transformation.

Parameters

gctx – The current geometry context object, e.g. alignment
lposition – is the local position to be transformed
direction – is the global momentum direction (ignored in this operation)

Returns

The global position by value

virtual Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const final

Return method for surface normal information.

Parameters

gctx – The current geometry context object, e.g. alignment
lposition – is the local position at normal vector request

Returns

Vector3 normal vector in global frame

virtual Vector3 normal(const GeometryContext &gctx, const Vector3 &position) const final

Return method for surface normal information.

Parameters

gctx – The current geometry context object, e.g. alignment
position – is the global position as normal vector base

Returns

Vector3 normal vector in global frame

Line surface¶

Acts::LineSurface is a special kind of surface that depends on a reference direction, typically the unit momentum direction \(\vec d\) of a particle. A point in space is considered on surface if and only if it coincides with the point of closest approach between the direction vector \(\vec d\) and the line direction vector \(\vec z\). As such, the function Acts::LineSurface::globalToLocal() can fail, if the argument position and direction do not fulfill this criterion. It is pure-virtual, meaning that it can not be instantiated on its own.

class LineSurface : public Acts::Surface

Base class for a linear surfaces in the TrackingGeometry to describe dirft tube, straw like detectors or the Perigee It inherits from Surface.

_build/doxygen-xml/LineSurface.png

Note

It leaves the type() method virtual, so it can not be instantiated

Subclassed by Acts::PerigeeSurface, Acts::StrawSurface

Public Functions

virtual Result<Vector2> globalToLocal(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, double tolerance = s_onSurfaceTolerance) const final

Specified for LineSurface: global to local method without dynamic memory allocation.

This method is the true global -> local transformation. It makes use of globalToLocal and indicates the sign of the Acts::eBoundLoc0 by the given momentum direction.

The calculation of the sign of the radius (or \( d_0 \)) can be done as follows: May \( \vec d = \vec m - \vec c \) denote the difference between the center of the line and the global position of the measurement/predicted state. Then, \( \vec d \) lies in the so-called measurement plane. The latter is determined by the two orthogonal vectors \( \vec{\texttt{measY}} = \vec{e}_z \) and \( \vec{\texttt{measX}} = \vec{\texttt{measY}} \times \frac{\vec{p}}{|\vec{p}|} \).

The sign of the radius (or \( d_{0} \) ) is then defined by the projection of \( \vec{d} \) on \( \vec{measX} \):\( sign = -sign(\vec{d} \cdot \vec{measX}) \)

_build/doxygen-xml/SignOfDriftCircleD0.gif

Parameters

gctx – The current geometry context object, e.g. alignment
position – global 3D position - considered to be on surface but not inside bounds (check is done)
direction – global 3D momentum direction (optionally ignored)
tolerance – (unused)

Returns

A Result<Vector2>, which is set to !ok() if the position is not the point of closest approach to the line surface.

virtual SurfaceIntersection intersect(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck = false, ActsScalar tolerance = s_onSurfaceTolerance) const final

Calculate the straight-line intersection with the line surface.

Mathematical motivation:

Given two lines in parameteric form:

\( \vec l_{a}(u) = \vec m_a + u \cdot \vec e_{a} \)

\( \vec l_{b}(\mu) = \vec m_b + \mu \cdot \vec e_{b} \)

The vector between any two points on the two lines is given by:

\( \vec s(u, \mu) = \vec l_{b} - l_{a} = \vec m_{ab} + \mu \cdot \vec e_{b} - u \cdot \vec e_{a} \),

where \( \vec m_{ab} = \vec m_{b} - \vec m_{a} \).

\( \vec s(u_0, \mu_0) \) denotes the vector between the two closest points

\( \vec l_{a,0} = l_{a}(u_0) \) and \( \vec l_{b,0} = l_{b}(\mu_0) \)

and is perpendicular to both, \( \vec e_{a} \) and \( \vec e_{b} \).

This results in a system of two linear equations:

(i) \( 0 = \vec s(u_0, \mu_0) \cdot \vec e_a = \vec m_{ab} \cdot \vec e_a + \mu_0 \vec e_a \cdot \vec e_b - u_0 \)
(ii) \( 0 = \vec s(u_0, \mu_0) \cdot \vec e_b = \vec m_{ab} \cdot \vec e_b + \mu_0 - u_0 \vec e_b \cdot \vec e_a \)

Solving (i) and (ii) for \( u \) and \( \mu_0 \) yields:

\( u_0 = \frac{(\vec m_{ab} \cdot \vec e_a)-(\vec m_{ab} \cdot \vec e_b)(\vec e_a \cdot \vec e_b)}{1-(\vec e_a \cdot \vec e_b)^2} \)
\( \mu_0 = - \frac{(\vec m_{ab} \cdot \vec e_b)-(\vec m_{ab} \cdot \vec e_a)(\vec e_a \cdot \vec e_b)}{1-(\vec e_a \cdot \vec e_b)^2} \)

The function checks if \( u_0 \simeq 0\) to check if the current position is at the point of closest approach, i.e. the intersection point, in which case it will return an onSurace intersection result. Otherwise, the path length from position to the point of closest approach ( \( u_0 \)) is returned in a reachable intersection.

Note

expected to be normalized

Parameters

gctx – The current geometry context object, e.g. alignment
position – The global position as a starting point
direction – The global direction at the starting point
bcheck – The boundary check directive for the estimate
tolerance – the tolerance used for the intersection

Returns

is the intersection object

virtual Vector3 localToGlobal(const GeometryContext &gctx, const Vector2 &lposition, const Vector3 &direction) const final

Local to global transformation.

Note

for line surfaces the momentum direction is used in order to interpret the drift radius

Parameters

gctx – The current geometry context object, e.g. alignment
lposition – is the local position to be transformed
direction – is the global momentum direction (used to sign the closest approach)

Returns

global position by value

virtual Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const final

The normal vector is undefined if we do not know the momentum.

Parameters

gctx – The current geometry context object, e.g. alignment
lposition – is the local position is ignored

Returns

a zero vector

Straw surface¶

class StrawSurface : public Acts::LineSurface

Class for a StrawSurface in the TrackingGeometry to describe dirft tube and straw like detectors.

_build/doxygen-xml/LineSurface.png

Perigee surface¶

class PerigeeSurface : public Acts::LineSurface

Class describing the Line to which the Perigee refers to.

The Surface axis is fixed to be the z-axis of the Tracking frame. It inherits from StraingLineSurface.

_build/doxygen-xml/LineSurface.png

Layer classes¶

The Acts::Layer class is an extension of the Acts::Surface class that allows the definition of sub surfaces (sensitive surfaces for modules, or extra material surfaces).

The layer can simply correspond to a ‘virtual’ surface in the detector description or represent a more complex object that may contain:

a representing surface, which is accessible via a Acts::Layer::surfaceRepresentation()
an array of contained surfaces, accessible via Acts::Layer::surfaceArray() method
approach surfaces (i.e. boundary surface of the volume occupied by the layer)
surface material description on any of the confined surfaces

The following illustration shows an \(xy\) view of a cylinder layer with planar detection modules:

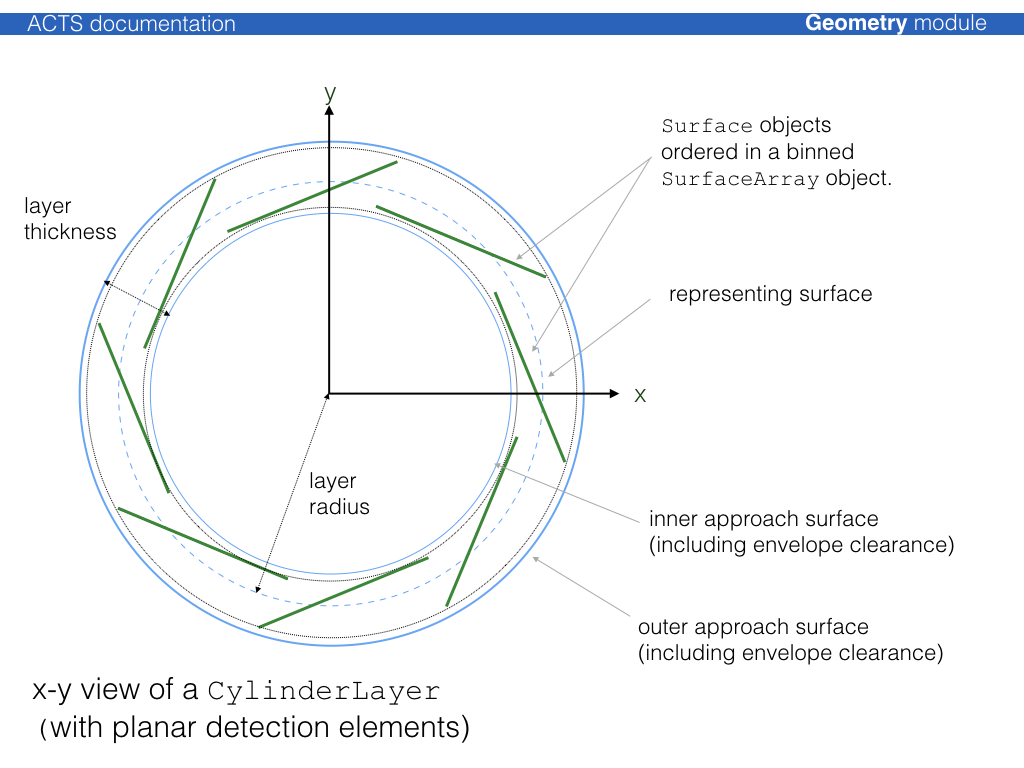
CylinderLayer

Modules can be sorted onto layer using all supported binning methods described through the Acts::SurfaceArray class. The binning can be adjusted to fit as well as possible.

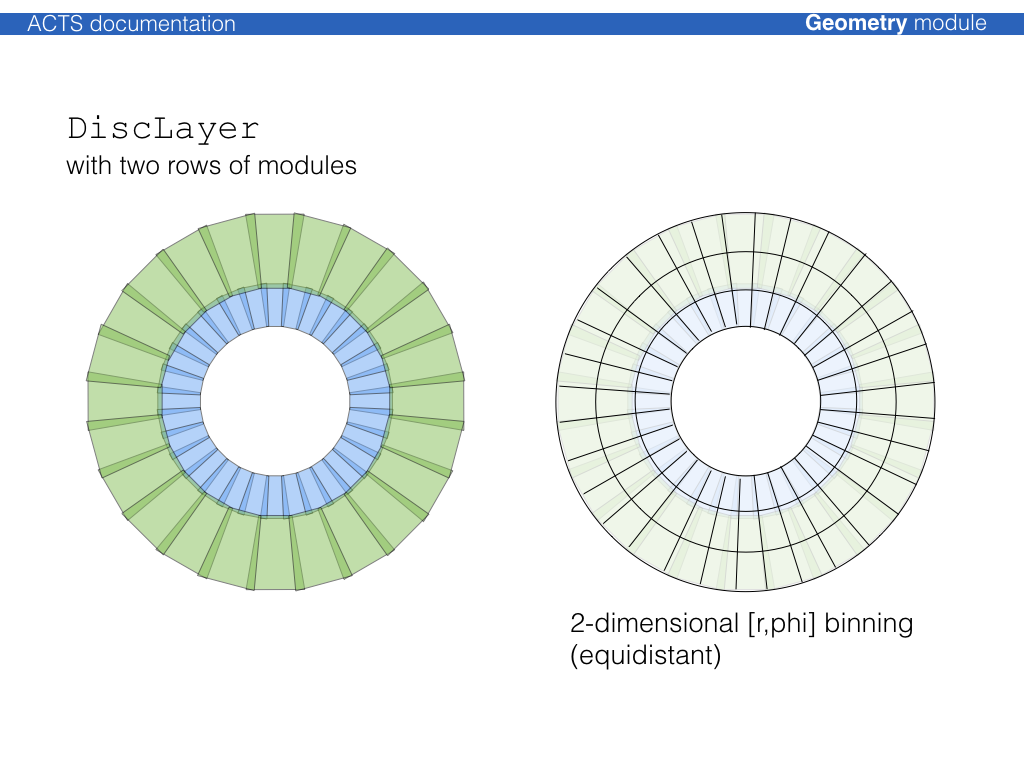
DiscLayerEB

The unoccupied space in a volume that contains a layer array is filled with objects of type Acts::NavigationLayer, which allows that in a fully static geometry setup, every single point in a volume can be associated with a layer. Layer objects are confined together in a special Acts::LayerArray class and can be contained by a Acts::TrackingVolume.

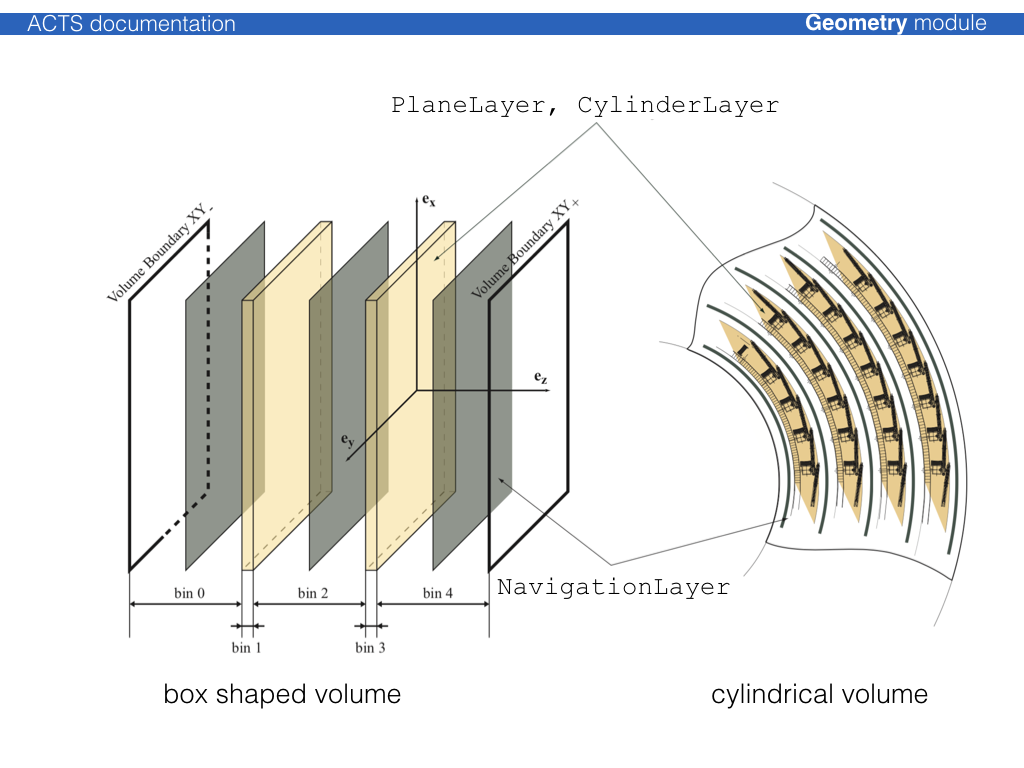
LayerArray

Volume classes¶

The Acts::Volume class is a container of Acts::BoundarySurface objects, where each Acts::BoundarySurface is an extension of the Acts::Surface class with additional information about the attached volumes. The normal vector of the surface defines an inside (opposite w.r.t. the normal vector) and an outside (along w.r.t. the normal vector) direction. Either a single volume or an array of volumes can be attached to a volume.

The simples volume class is just a collection of surfaces, where the Acts::TrackingVolume describes a volume that can contain:

an array of contained layers
an array of contained volumes (as a container volume)
an array of contained volumes (as floating objects)
a volume based material description

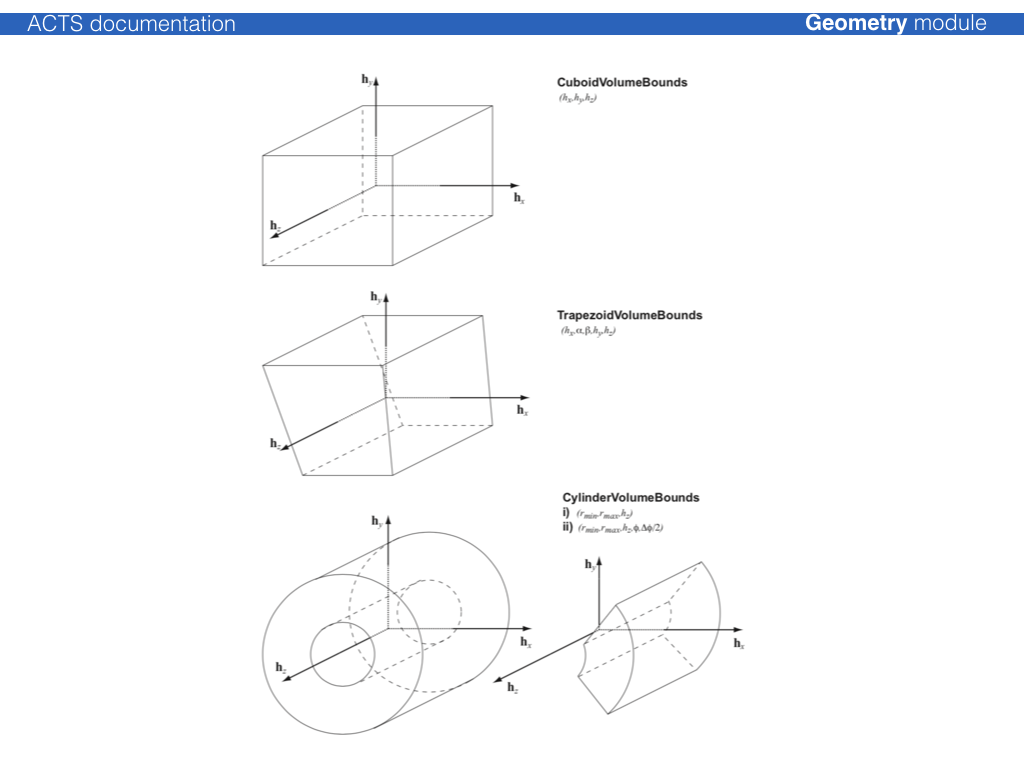
The shape of the volume is defined by Acts::VolumeBounds classes that create the corresponding bounding surfaces and register the attachment to the volume itself at creation.

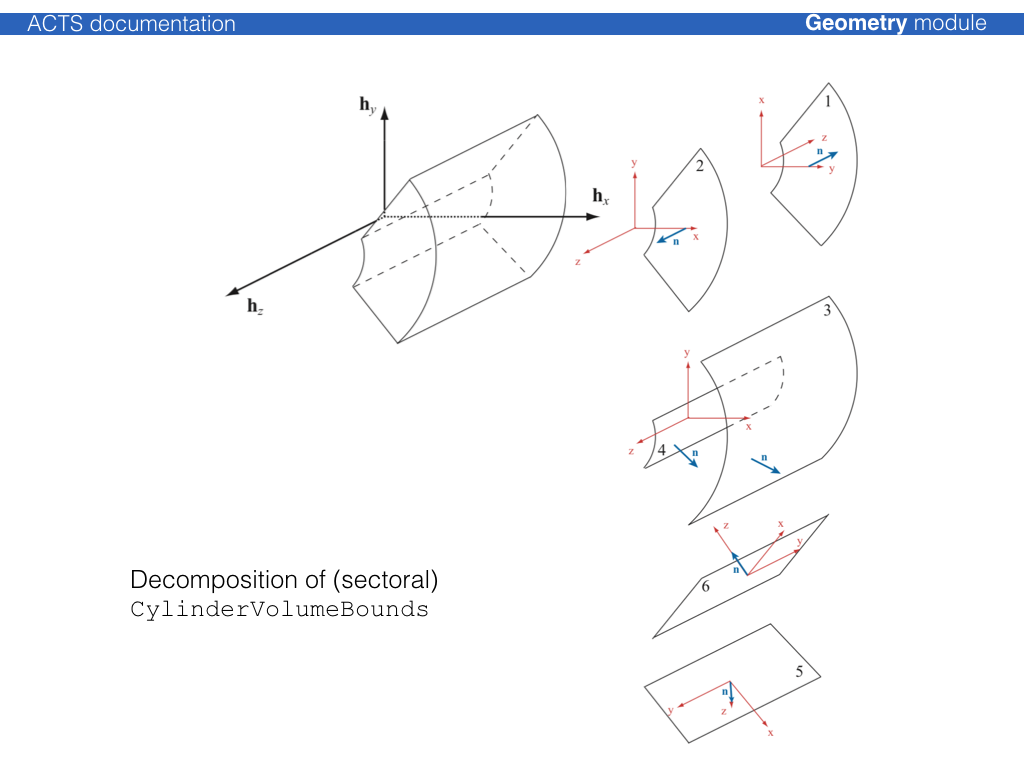
VolumeBounds CylinderVolumeBounds

Detector material description¶

Two types of material description exist, one for a surface based material, one for a volume based material. They will be dealt with differently in the extrapolation.

The basic information for any material is:

the radiation length X0 the nuclear interaction length L0 the atomic weight A
the atomic charge Z the density of the material

This information is confined together in the Acts::Material class.

Note

In track reconstruction, only an effective material description is needed, i.e. non-physical values in regards of the atomic number, the elementary charge or even the density are allowed, as long as the effective relative radiation length and \(A/Z \times \rho\) ratio can be retrieved. This enables the compactification of the material description, as the element composition record does not have to be kept.

Surface based material extends this material information by a representative thickness; the corresponding object is called Acts::MaterialSlab. The thickness hereby can be arbitrarily chosen in order to regulate the material budget, it does not have to represent the actual thickness of a detector element. To attach it to a surface, a dedicated Acts::SurfaceMaterial class (or it’s extensions) is used, which allows to also describe binned material.

Possible extensions are:

Acts::HomogeneousSurfaceMaterial, homogeneous material description on a surface
Acts::BinnedSurfaceMaterial, an arbitrarily binned material description with a corresponding Acts::BinUtility object

In addition, a dedicated extension exists to allow configuration of the material mapping process, that is in further described below.

Acts::ProtoSurfaceMaterial, only binning description (without material) to be used in the material mapping process

Geometry building¶

The geometry building procedure follows the ATLAS tracking geometry philosophy of a static frame of glued volumes, that lead the navigation flow through the geometry,

Attaching a 3D detector geometry¶

Usually, a 3D detector model geometry exists, which is either native to the full detector simulation (Geant4) or is translated into it. This model, however, is in general too detailed for track reconstruction: navigating through the detailed detector geometry is generally costly and one can profit greatly from a simplification mechanism.

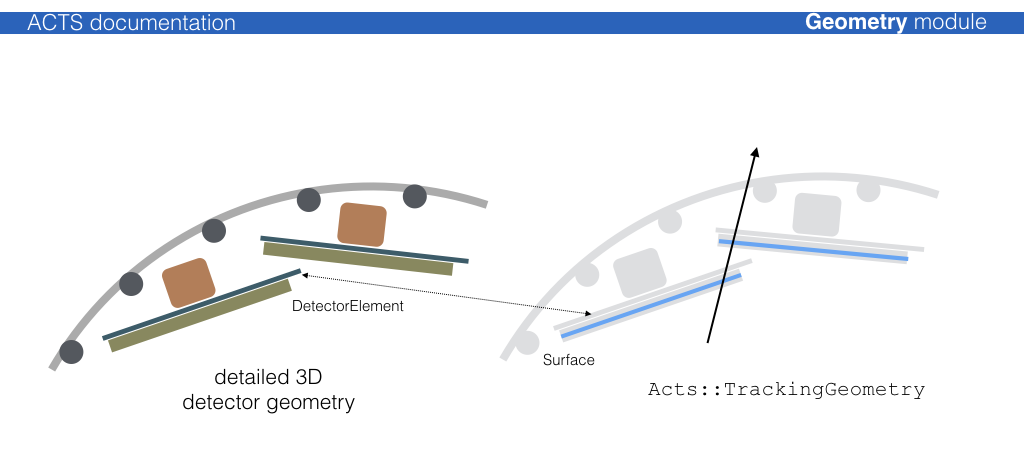
For most part of the track reconstruction, only a surface based description of the detector is needed, in order to allow (surface based) material integration and parametrization/prediction of trajectories on detection surfaces. It is thus necessary that the detection surfaces are described to full detail in the reconstruction geometry (called Acts::TrackingGeometry). This is guaranteed by a proxy mechanism that connects the detection elements (conveniently called Acts::DetectorElement) to Acts::Surface object in the reconstruction:

DetectorElement

Existing plugins for 3D geometry libraries¶

Very simple helper methods for 3D libraries exist, they are certainly not optimised, but used for templating:

Acts::TGeoDetectorElement connects a TGeo volume to a Acts::Surface
Acts::DD4HepDetectorElement connects a DD4hep volume (based on TGeo) to a Acts::Surface
Acts::Geant4DetectorElement connects a Geant4 volume to a Acts::Surface

Further extensions exist in dedicated experiment contexts, such as e.g. a GeoModel binding for the ATLAS experiment.

Note

While DD4hep offers a descriptive language with a dedicated extension mechanism that can be used by Acts to interpret the underlying geometry hierarchy and and structure, there is no such guarantee when having the already as built TGeo geometry in hand. Therefore a dedicated Acts configuration file based on json can be provided that allows to specify parsing restrictions for sub detectors.

Layer building¶

Acts::Surface objects that are to be grouped on a layer should be put into a Acts::SurfaceArray and provided to the layer. Certain helper tools exist to ease the translation and create appropriate binning structure: The Acts::SurfaceArrayCreator can create cylindrical, disc-like & planar layers, where the dimensions of the layer are determined by parsing the provided surfaces. Additionally, an envelope covering the surfaces can be chosen.

Note

There exist standard layer builders that are designed to build cylindrical, disk like and planar layers and perform the ordering of the surfaces onto those layers. These builders are called from the top level translation entry points from either TGeo or DD4hep.

Volume building, packing, and gluing¶

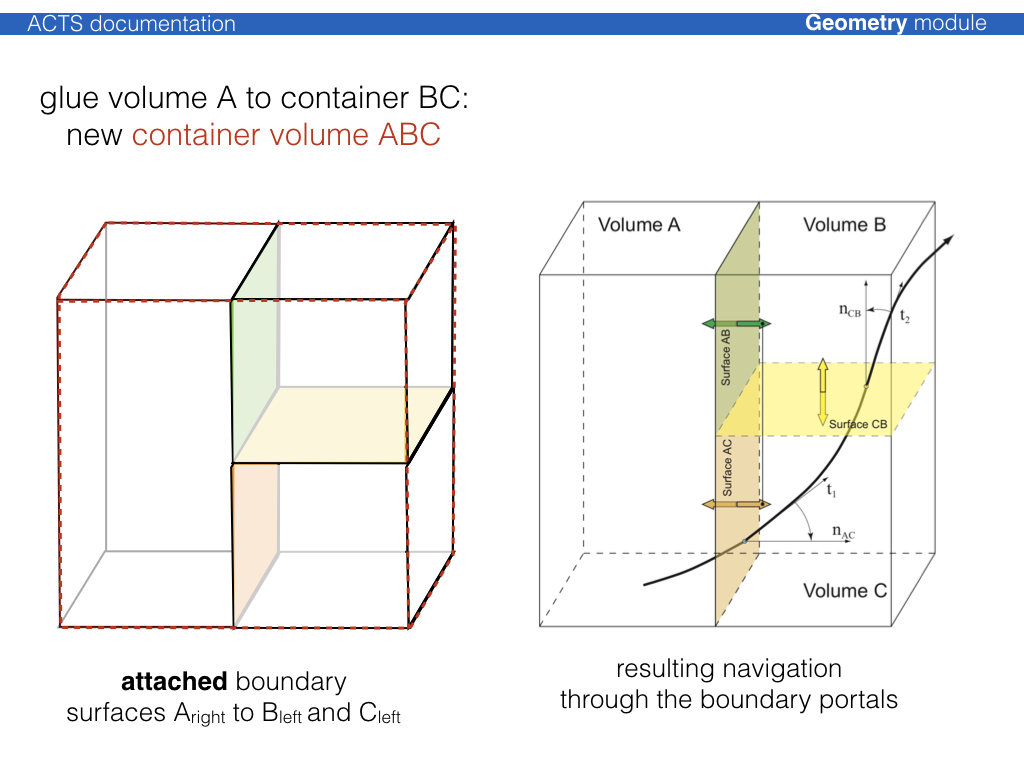
The philosophy of the Acts::TrackingGeometry is a fully connective geometry setup, i.e. Acts::TrackingVolume objects are either pure containers for other contained Acts::TrackingVolume instances (where the contained volumes fully fill the space of the container volume), or are fully attached via the boundary surface mechanism. The boundary surfaces then act as portals from one Acts::TrackingVolume into the next one along the trajectory.

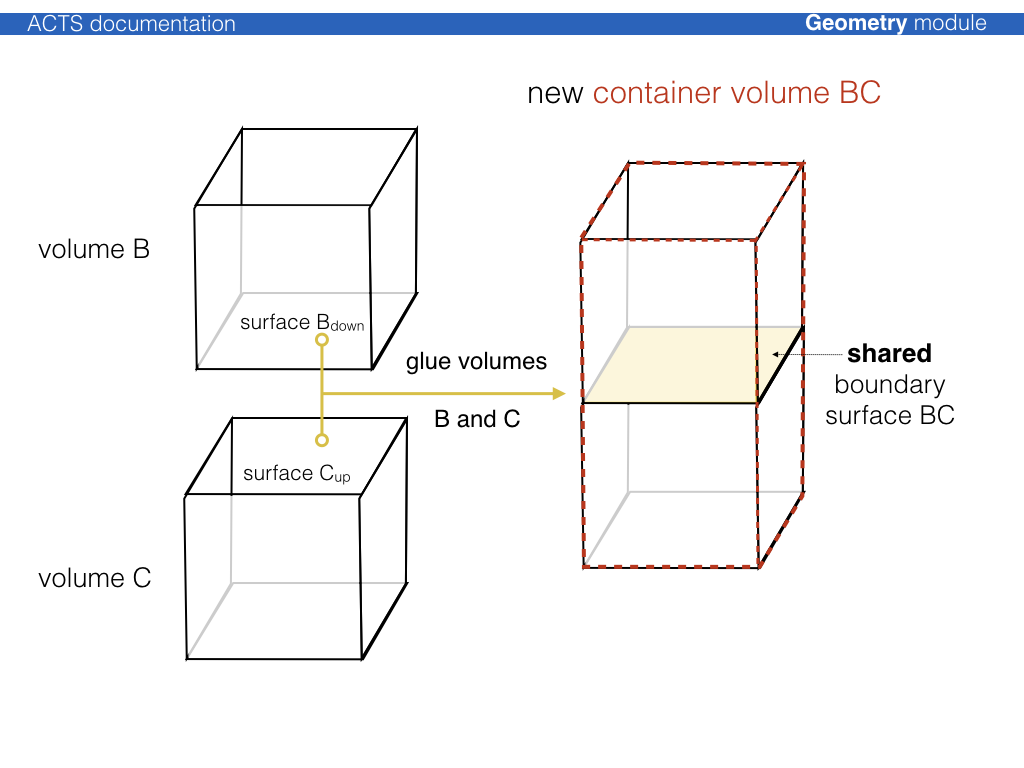
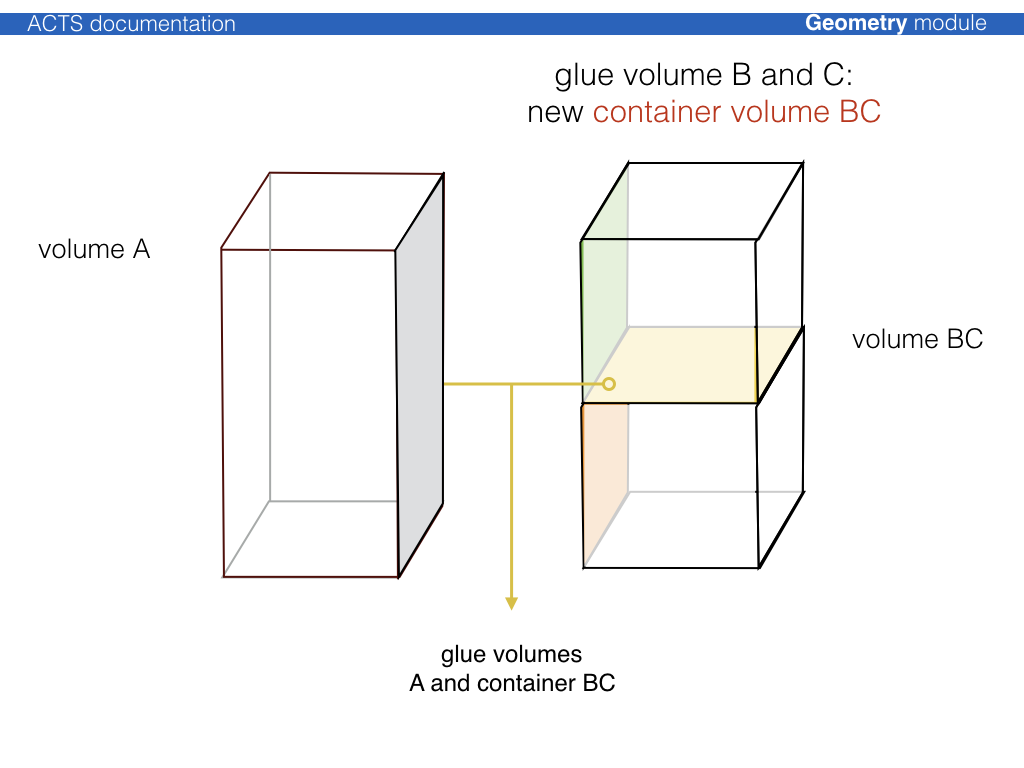
The process to create a fully connected tracking geometry is called glueing. Wherever possible, common boundary surfaces are shared, where this is not possible, they are attached.

GlueingBC GlueingABC NavigationABC

For cylindrical detector setups, a dedicated Acts::CylinderVolumeBuilder is provided, which performs a variety of volume building, packing and gluing.

Note

For most cylindrical detectors, there exist automated glueing and geometry building modules that take care of the glueing process.

TrackingGeometry building using a KDTree and a Proto Description¶

For cylindrical detectors there exist a generic tracking geometry building module, based on KDTree and a proto description.

This building procedure uses a Acts::ProtoDetector description which provides a high level description of layers and container volumes, together with some binning and ordering information. This proto description is then used to assign surfaces that are provided to the Acts::KDTreeTrackingGeometryBuilder using an internal query to the KD-tree structure.