Magnetic field

The magnetic field component of ACTS provides functionality to describe arbitrary magnetic field configurations in an experiment. It is implemented in a generic way and can be extended to connect to an experiment specific upstream source of field data.

Algorithms which need magnetic field information (e.g. Acts::AtlasStepper, Acts::EigenStepper) accept the magnetic field as an explicit argument.

Provider interface

All magnetic field implementations inherit and implement the interface Acts::MagneticFieldProvider:

It provides a generic interface over different implementations. To speed up magnetic field lookup, each implementation can have a cache object. The cache object can for example be used to store a local interpolation domain, to speed up nearby field lookups. The client is expected to pass into lookup calls:

using Acts::MagneticFieldProvider::Cache = Acts::AnyBase<sizeof(char) * 512>

Opaque cache type that can store arbitrary implementation specific cache data.

Examples are an interpolation cell, or an experiment specific conditions data handle.

The implementation is then free to use and update this cache instance as needed. Before a client can issue field lookup calls, it needs to obtain an initialized instance of this cache object. This can be achieved generically for all implementations by using Acts::MagneticFieldProvider::makeCache(). This function accepts an instance of Acts::MagneticFieldContext, see Magnetic field context for details.

The main lookup method of Acts::MagneticFieldProvider is

virtual Result<Vector3> Acts::MagneticFieldProvider::getField(const Vector3 &position, Cache &cache) const = 0

Aside from the lookup position as a global position vector, it accepts an instance of the opaque cache object mentioned before. The return value is a Acts::Result object. It either contains the field value at the requested location, or an Acts::MagneticFieldError in case of a lookup failure, like an out-of-bounds lookup position.

Below is an example of how a client can interact with an instance of Acts::MagneticFieldProvider.

// in event context
auto fieldContext = getExperimentFieldContext();
const Acts::MagneticFieldProvider& fieldProvider = getFieldProvider();
auto cache = fieldProvider.makeCache(fieldContext);

auto lookupResult = fieldProvider.getField(Acts::Vector3{10, 10, 10}, cache);
if(!lookupResult.ok()) {
   throw std::runtime_error{"Field lookup failure"};
}

Acts::Vector3 fieldValue = *lookupResult;

Magnetic field context

class MagneticFieldContext : public ContextType

The magnetic field context is an opaque type which contains experiment specific event context information. This can be used to supply event dependent data to the magnetic field instance, in case it is needed to provide correct field values. The library itself does not make any assumptions on the content of this context type (it is implemented using std::any), but passes a reference through the call-chain to the field implementation. An experiment specific field implementation is then expected to performa cast to the concrete type, and use the contents.

An example use case of the context could be to look up conditions data / records for the value of the magnetic field at the time of the event.

Field provider implementations in Core

There are a number of field provider implementations found in core which serve different purposes.

Constant magnetic field

The simplest implementation is a constant field, which returns the same field values at every queried location. It is implemented in the Acts::ConstantBField class.

class ConstantBField : public Acts::MagneticFieldProvider

This class implements a simple constant magnetic field.

The magnetic field value has to be set at creation time, but can be updated later on.

Public Functions

inline explicit ConstantBField(Vector3 B)

Construct constant magnetic field from field vector.

Parameters:

B – [in] magnetic field vector in global coordinate system

As seen above, the class is constructed from a three-dimensional field vector, which is returned unmodified to every call to Acts::ConstantBField::getField().

Interpolated magnetic field

For more complex magnetic field implementations Acts::InterpolatedMagneticField can be used. The idea here is to calculate an interpolated value of the magnetic field from a grid of known field values. In 3D, this means the interpolation is done from the 8 corner points of a field cell. The field cell can be retrieved for any given position. Since during typical access patterns, e.g. the propagation, subsequent steps are relatively likely to not cross the field cell boundary, the field cell can be cached.

../_images/field_cell.svg

Fig. 27 Illustration of the field cell concept. Subsequent steps are clustered in the same field cell. The field cell only needs to be refetched when the propagation crosses into the next grid region.

Acts::InterpolatedMagneticField extends the Acts::MagneticFieldProvider interface to add a number of additional methods:

class InterpolatedMagneticField : public Acts::MagneticFieldProvider

Subclassed by Acts::InterpolatedBFieldMap< grid_t >

Public Functions

virtual Vector3 getFieldUnchecked(const Vector3 &position) const = 0

Get a field value without checking if the lookup position is within the interpolation domain.

Parameters:

position – The lookup position in 3D

Returns:

The field value at position

virtual std::vector<double> getMax() const = 0

get the maximum value of all axes of the field map

Returns:

vector returning the maxima of all field map axes

virtual std::vector<double> getMin() const = 0

get the minimum value of all axes of the field map

Returns:

vector returning the minima of all field map axes

virtual std::vector<std::size_t> getNBins() const = 0

get the number of bins for all axes of the field map

Returns:

vector returning number of bins for all field map axes

virtual bool isInside(const Vector3 &position) const = 0

check whether given 3D position is inside look-up domain

Parameters:

position – [in] global 3D position

Returns:

true if position is inside the defined look-up grid, otherwise false

This intermediate interface is again implemented by Acts::InterpolatedBFieldMap, which is a template class that depends on an instance of Acts::Grid. Varying configurations are possible, like a 2D field map that exploits \(rz\) symmetry, or a plain 3D grid.

template<typename grid_t>
class InterpolatedBFieldMap : public Acts::InterpolatedMagneticField

interpolate magnetic field value from field values on a given grid

This class implements a magnetic field service which is initialized by a field map defined by:

  • a list of field values on a regular grid in some n-Dimensional space,

  • a transformation of global 3D coordinates onto this n-Dimensional space.

  • a transformation of local n-Dimensional magnetic field coordinates into global (cartesian) 3D coordinates

The magnetic field value for a given global position is then determined by:

  • mapping the position onto the grid,

  • looking up the magnetic field values on the closest grid points,

  • doing a linear interpolation of these magnetic field values.

Template Parameters:

grid_t – The Grid type which provides the field storage and interpolation

The class constructor accepts a single configuration struct that contains the grid instance, a scale factor and optional conversion function for the lookup positions and the returned field values.

struct Config

Config structure for the interpolated B field map.

Public Members

Grid grid

grid storing magnetic field values

double scale = 1.

global B-field scaling factor

Note

Negative values for scale are accepted and will invert the direction of the magnetic field.

std::function<Vector3(const FieldType&, const Vector3&)> transformBField

calculating the global 3D coordinates (cartesian) of the magnetic field with the local n dimensional field and the global 3D position as input

std::function< ActsVector< DIM_POS >const Vector3 &)> transformPos

mapping of global 3D coordinates (cartesian) onto grid space

Internally, Acts::InterpolatedBFieldMap uses a field interpolation cell to speed up lookups. This cell contains the interpolation points so the grid does not have to be consulted for each lookup. Explicit methods to create such a field cell are provided, but field cell creation is automatically handled by Acts::InterpolatedBFieldMap::makeCache(), opaque to the client.

Helpers to construct an interpolated field map from text and ROOT file inputs are provided:

Acts::InterpolatedBFieldMap<Acts::Grid<Acts::Vector2, Acts::Axis<Acts::AxisType::Equidistant>, Acts::Axis<Acts::AxisType::Equidistant>>> Acts::fieldMapRZ(const std::function<std::size_t(std::array<std::size_t, 2> binsRZ, std::array<std::size_t, 2> nBinsRZ)> &localToGlobalBin, std::vector<double> rPos, std::vector<double> zPos, std::vector<Acts::Vector2> bField, double lengthUnit = UnitConstants::mm, double BFieldUnit = UnitConstants::T, bool firstQuadrant = false)

Method to setup the FieldMap.

e.g.: we have small grid with the values: r={2,3}, z ={4,5}, the corresponding indices are i (belonging to r) and j (belonging to z), the globalIndex is M (belonging to the value of the magnetic field B(r,z)) and the field map is:

r

i

z

j

B(r,z)

M

2

0

4

0

2.323

0

2

0

5

1

2.334

1

3

1

4

0

2.325

2

3

1

5

1

2.331

3

In this case the function would look like: 

[](std::array<std::size_t, 2> binsRZ, std::array<std::size_t, 2> nBinsRZ) {
   return (binsRZ.at(0) * nBinsRZ.at(1) + binsRZ.at(1));
}

Note

The values do not need to be sorted or unique (this will be done inside the function)

Note

The values do not need to be sorted or unique (this will be done inside the function)

Note

The function localToGlobalBin determines how the magnetic field was stored in the vector in respect to the grid values

Note

If firstQuadrant is true will create a field that is symmetric for all quadrants. e.g. we have the grid values r={0,1} with BFieldValues={2,3} on the r axis. If the flag is set to true the r-axis grid values will be set to {-1,0,1} and the BFieldValues will be set to {3,2,3}.

Parameters:

  • localToGlobalBin – Function mapping the local bins of r,z to the global bin of the map magnetic field value

  • rPos – [in] Values of the grid points in r

  • zPos – [in] Values of the grid points in z

  • bField – [in] The magnetic field values inr r and z for all given grid points stored in a vector

  • lengthUnit – [in] The unit of the grid points

  • BFieldUnit – [in] The unit of the magnetic field

  • firstQuadrant – [in] Flag if set to true indicating that only the first quadrant of the grid points and the BField values has been given.

Returns:

A field map instance for use in interpolation.

Acts::InterpolatedBFieldMap<Acts::Grid<Acts::Vector3, Acts::Axis<Acts::AxisType::Equidistant>, Acts::Axis<Acts::AxisType::Equidistant>, Acts::Axis<Acts::AxisType::Equidistant>>> Acts::fieldMapXYZ(const std::function<std::size_t(std::array<std::size_t, 3> binsXYZ, std::array<std::size_t, 3> nBinsXYZ)> &localToGlobalBin, std::vector<double> xPos, std::vector<double> yPos, std::vector<double> zPos, std::vector<Acts::Vector3> bField, double lengthUnit = UnitConstants::mm, double BFieldUnit = UnitConstants::T, bool firstOctant = false)

Method to setup the FieldMap.

e.g.: we have small grid with the values: x={2,3}, y={3,4}, z ={4,5}, the corresponding indices are i (belonging to x), j (belonging to y) and k (belonging to z), the globalIndex is M (belonging to the value of the magnetic field B(x,y,z)) and the field map is:

x

i

y

j

z

k

B(x,y,z)

M

2

0

3

0

4

0

2.323

0

2

0

3

0

5

1

2.334

1

2

0

4

1

4

0

2.325

2

2

0

4

1

5

1

2.331

3

3

1

3

0

4

0

2.323

4

3

1

3

0

5

1

2.334

5

3

1

4

1

4

0

2.325

6

3

1

4

1

5

1

2.331

7

In this case the function would look like: 

[](std::array<std::size_t, 3> binsXYZ, std::array<std::size_t, 3> nBinsXYZ)
{
  return (binsXYZ.at(0) * (nBinsXYZ.at(1) * nBinsXYZ.at(2))
       + binsXYZ.at(1) * nBinsXYZ.at(2)
       + binsXYZ.at(2));
}

Note

The grid point values xPos, yPos and zPos do not need to be sorted or unique (this will be done inside the function)

Note

The function localToGlobalBin determines how the magnetic field was stored in the vector in respect to the grid values

Note

If firstOctant is true, the function will assume a symmetrical field for all quadrants. e.g. we have the grid values z={0,1} with BFieldValues={2,3} on the r axis. If the flag is set to true the z-axis grid values will be set to {-1,0,1} and the BFieldValues will be set to {3,2,3}.

Parameters:

  • localToGlobalBin – Function mapping the local bins of x,y,z to the global bin of the map magnetic field value

  • xPos – [in] Values of the grid points in x

  • yPos – [in] Values of the grid points in y

  • zPos – [in] Values of the grid points in z

  • bField – [in] The magnetic field values inr r and z for all given grid points stored in a vector

  • lengthUnit – [in] The unit of the grid points

  • BFieldUnit – [in] The unit of the magnetic field

  • firstOctant – [in] Flag if set to true indicating that only the first octant of the grid points and the BField values has been given.

Returns:

A field map instance for use in interpolation.

Analytical solenoid magnetic field

Warning

The analytical solenoid field is slow. See Acts::solenoidFieldMap() to speed it up.

ACTS also provides a field provider that calculates the field vectors analytically for a solenoid field.

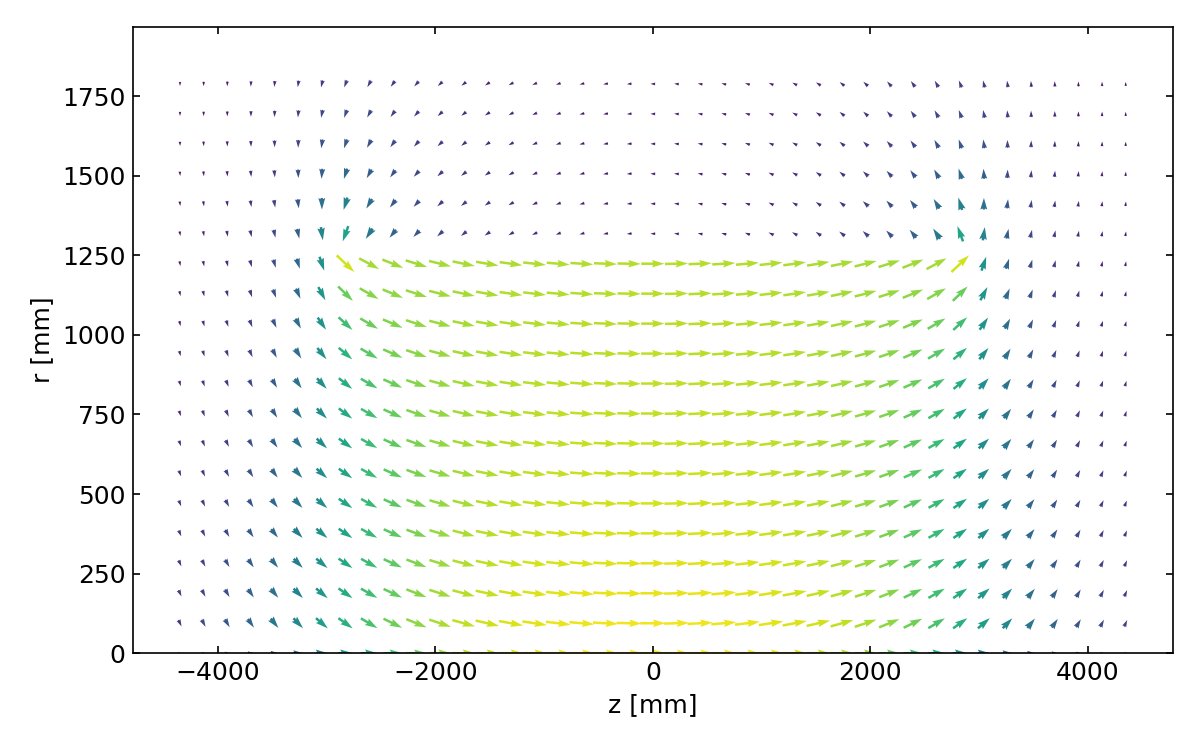
../_images/quiver.png

Fig. 28 Picture of a solenoid field in rz, with arrows indicating the direction of the field, and their size denoting the strength. The field is almost homogeneous in the center.

The implementation has configurable solenoid parameters:

struct Config

Config struct for the SolenoidBfield.

Public Members

double bMagCenter

The target magnetic field strength at the center.

This will be used to scale coefficients

double length

Extent of the solenoid in z.

It goes from -length/2 to +length/2 by convention

std::size_t nCoils

The number of coils that make up the solenoid.

double radius

Radius at which the coils are located.

Note

A configuration of

SolenoidBField::Config cfg;
cfg.length = 5.8_m;
cfg.radius = (2.56 + 2.46) * 0.5 * 0.5_m;
cfg.nCoils = 1154;
cfg.bMagCenter = 2_T;
SolenoidBField bField(cfg);

roughly corresponds to the solenoid wrapping the Inner Detector in ATLAS.

Implementation

The calculation uses two special functions:

  • \(E_1(k^2)\) is the complete elliptic integral of the 1st kind

  • \(E_2(k^2)\) is the complete elliptic integral of the 2nd kind

\(E_1(k^2)\) and \(E_2(k^2)\) are usually indicated as \(K(k^2)\) and \(E(k^2)\) in literature, respectively:

\[ E_1(k^2) = \int_0^{\pi/2} \left( 1 - k^2 \sin^2{\theta} \right )^{-1/2} \mathop{}\!\mathrm{d}\theta \]
\[ E_2(k^2) = \int_0^{\pi/2}\sqrt{1 - k^2 \sin^2{\theta}} \mathop{}\!\mathrm{d}\theta \]

\(k^2\) is a function of the point \((r, z)\) and of the radius of the coil \(R\)

\[ k^2 = \frac{4Rr}{(R+r)^2 + z^2} \]

Using these, you can evaluate the two components \(B_r\) and \(B_z\) of the magnetic field:

\[ B_r(r, z) = \frac{\mu_0 I}{4\pi} \frac{kz}{\sqrt{Rr^3}} \left[ \left(\frac{2-k^2}{2-2k^2}\right)E_2(k^2) - E_1(k^2) \right ] \]
\[ B_z(r,z) = \frac{\mu_0 I}{4\pi} \frac{k}{\sqrt{Rr}} \left[ \left( \frac{(R+r)k^2-2r}{2r(1-k^2)} \right ) E_2(k^2) + E_1(k^2) \right ] \]

In the implementation the factor of \((\mu_0\cdot I)\) is defined to be a scaling factor. It is evaluated and defined as the magnetic field in the center of the coil, i.e. the scale set in Acts::SolenoidBField::Config::bMagCenter.

As the evaluation of \(E_1(k^2)\) and \(E_2(k^2)\) is slow. The Acts::InterpolatedBFieldMap easily outperforms Acts::SolenoidBField. A helper is provided that builds a map from the analytical implementation and is much faster to lookup:

Acts::InterpolatedBFieldMap<Acts::Grid<Acts::Vector2, Acts::Axis<Acts::AxisType::Equidistant>, Acts::Axis<Acts::AxisType::Equidistant>>> Acts::solenoidFieldMap(std::pair<double, double> rlim, std::pair<double, double> zlim, std::pair<std::size_t, std::size_t> nbins, const SolenoidBField &field)

Function which takes an existing SolenoidBField instance and creates a field mapper by sampling grid points from the analytical solenoid field.

Parameters:

  • rlim – pair of r bounds

  • zlim – pair of z bounds

  • nbins – pair of bin counts

  • field – the solenoid field instance

Returns:

A field map instance for use in interpolation.

Full provider interface

class MagneticFieldProvider

Base class for all magnetic field providers.

Subclassed by Acts::ConstantBField, Acts::DD4hepFieldAdapter, Acts::InterpolatedMagneticField, Acts::NullBField, Acts::SolenoidBField

Public Types

using Cache = Acts::AnyBase<sizeof(char) * 512>

Opaque cache type that can store arbitrary implementation specific cache data.

Examples are an interpolation cell, or an experiment specific conditions data handle.

Public Functions

inline virtual ~MagneticFieldProvider()
virtual Result<Vector3> getField(const Vector3 &position, Cache &cache) const = 0

Retrieve magnetic field value at a given location.

Requires a cache object created through makeCache().

Parameters:

  • position – [in] global 3D position for the lookup

  • cache – [inout] Field provider specific cache object

Returns:

magnetic field vector at given position

virtual Result<Vector3> getFieldGradient(const Vector3 &position, ActsMatrix<3, 3> &derivative, Cache &cache) const = 0

Retrieve magnetic field value its its gradient.

Requires a cache object created through makeCache().

Parameters:

  • position – [in] global 3D position

  • derivative – [out] gradient of magnetic field vector as (3x3) matrix

  • cache – [inout] Field provider specific cache object

Returns:

magnetic field vector

virtual Cache makeCache(const MagneticFieldContext &mctx) const = 0

Make an opaque cache for the magnetic field.

Instructs the specific implementation to generate a Cache instance for magnetic field lookup.

Parameters:

mctx – The magnetic field context to generate cache for

Returns:

Cache The opaque cache object