Namespace Acts
-
namespace Acts
Note
This file is foreseen for the
Geometrymodule to replaceExtentTypedefs
-
using ActsDynamicMatrix = Eigen::Matrix<ActsScalar, Eigen::Dynamic, Eigen::Dynamic>
-
using ActsDynamicVector = Eigen::Matrix<ActsScalar, Eigen::Dynamic, 1>
-
template<unsigned int kRows, unsigned int kCols>
using ActsMatrix = Eigen::Matrix<ActsScalar, kRows, kCols>
-
using ActsScalar = double
Common scalar (floating point type used for the default algebra types.
Defaults to
doublebut can be customized by the user.
-
template<unsigned int kSize>
using ActsSquareMatrix = Eigen::Matrix<ActsScalar, kSize, kSize>
-
template<unsigned int kSize>
using ActsVector = Eigen::Matrix<ActsScalar, kSize, 1>
-
using AlignmentMatrix = ActsMatrix<eAlignmentSize, eAlignmentSize>
-
using AlignmentRowVector = ActsMatrix<1, eAlignmentSize>
-
using AlignmentToBoundMatrix = ActsMatrix<eBoundSize, eAlignmentSize>
-
using AlignmentToPathMatrix = ActsMatrix<1, eAlignmentSize>
-
using AlignmentToPositionMatrix = ActsMatrix<3, eAlignmentSize>
-
using AlignmentVector = ActsVector<eAlignmentSize>
-
using AngleAxis3 = Eigen::AngleAxis<ActsScalar>
-
using Any = AnyBase<sizeof(void*)>
-
using AxisScalar = Vector3::Scalar
-
using BoundaryIntersection = ObjectIntersection<BoundarySurface, Surface>
Intersection with a
BoundarySurface.
-
using BoundarySurface = BoundarySurfaceT<TrackingVolume>
BoundarySurface of a volume.
-
using BoundarySurfacePtr = std::shared_ptr<const BoundarySurfaceT<AbstractVolume>>
-
using BoundMatrix = ActsMatrix<eBoundSize, eBoundSize>
-
using BoundSquareMatrix = ActsSquareMatrix<eBoundSize>
-
using BoundToFreeMatrix = ActsMatrix<eFreeSize, eBoundSize>
-
using BoundTrackParameters = GenericBoundTrackParameters<SinglyCharged>
-
using BoundVariantMeasurement = VariantMeasurement<BoundIndices>
Variant that can hold all possible bound measurements.
-
using BoundVector = ActsVector<eBoundSize>
-
using CalibrationContext = std::any
This is the central definition of the Acts payload object regarding detector calibration.
It is propagated through the code to allow for event/thread dependent calibration
-
using ColorRGB = std::array<int, 3>
The color typedef.
It’s an array of three numbers [0, 255] representing the RGB color values.
-
template<typename T>
using ConstTrackAccessor = TrackAccessorBase<T, true>
-
using CurvilinearTrackParameters = GenericCurvilinearTrackParameters<SinglyCharged>
-
using DefaultExtension = detail::GenericDefaultExtension<double>
A typedef for the default GenericDefaultExtension with double.
-
using DenseEnvironmentExtension = detail::GenericDenseEnvironmentExtension<double>
A typedef for the default GenericDenseEnvironmentExtension with double.
-
using EAxis = Acts::detail::EquidistantAxis
-
using Envelope = std::array<ActsScalar, 2>
-
using FreeMatrix = ActsMatrix<eFreeSize, eFreeSize>
-
using FreeSquareMatrix = ActsSquareMatrix<eFreeSize>
-
using FreeToBoundMatrix = ActsMatrix<eBoundSize, eFreeSize>
-
using FreeToPathMatrix = ActsMatrix<1, eFreeSize>
-
using FreeTrackParameters = GenericFreeTrackParameters<SinglyCharged>
-
using FreeVariantMeasurement = VariantMeasurement<FreeIndices>
Variant that can hold all possible free measurements.
-
using FreeVector = ActsVector<eFreeSize>
-
using GeometryContext = ContextType
This is the central definition of the Acts payload object regarding detector geometry status (e.g.
alignment)
It is propagated through the code to allow for event/thread dependent geometry changes
-
using Grid2D = Acts::detail::Grid<Acts::AccumulatedVolumeMaterial, EAxis, EAxis>
-
using HashedString = std::uint32_t
-
using Intersection2D = Intersection<2>
-
using Intersection3D = Intersection<3>
-
typedef BinnedArray<LayerPtr> LayerArray
A BinnedArray to a std::shared_ptr of a layer.
Layers are constructed with shared_ptr factories, hence the layer array is describes as:
-
using LayerIntersection = ObjectIntersection<Layer, Surface>
-
typedef std::shared_ptr<const Layer> LayerPtr
A std::shared_ptr to a Layer.
-
typedef std::vector<LayerPtr> LayerVector
A vector of std::shared_ptr to layers.
-
using MagneticFieldContext = ContextType
This is the central definition of the Acts payload object regarding magnetic field status.
It is propagated through the code to allow for event/thread dependent magnetic field changes
-
using MaterialGridAxisData = std::tuple<double, double, size_t>
-
using MaterialSlabMatrix = std::vector<MaterialSlabVector>
-
using MaterialSlabVector = std::vector<MaterialSlab>
-
typedef std::shared_ptr<Layer> MutableLayerPtr
-
typedef std::shared_ptr<TrackingVolume> MutableTrackingVolumePtr
-
typedef std::vector<MutableTrackingVolumePtr> MutableTrackingVolumeVector
-
using NetworkBatchInput = Eigen::Array<float, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>
-
using NeutralBoundTrackParameters = GenericBoundTrackParameters<Neutral>
-
using NeutralCurvilinearTrackParameters = GenericCurvilinearTrackParameters<Neutral>
-
using NeutralFreeTrackParameters = GenericFreeTrackParameters<Neutral>
-
using OrientedSurfaces = std::vector<OrientedSurface>
-
using ProjectorBitset = uint64_t
-
using Ray3D = Ray<ActsScalar, 3>
-
using RecordedMaterialTrack = std::pair<std::pair<Acts::Vector3, Acts::Vector3>, RecordedMaterial>
And recorded material track.
this is start: position, start momentum and the Recorded material
-
using RecordedMaterialVolumePoint = std::vector<std::pair<Acts::MaterialSlab, std::vector<Acts::Vector3>>>
list of point used in the mapping of a volume
-
using RotationMatrix2 = ActsMatrix<2, 2>
-
using RotationMatrix3 = ActsMatrix<3, 3>
-
template<typename source_link_iterator_t>
using SourceLinkAccessorDelegate = Delegate<std::pair<source_link_iterator_t, source_link_iterator_t>(const Surface&)> Delegate type that retrieves a range of source links to for a given surface to be processed by the CKF.
-
using SourceLinkSurfaceAccessor = Delegate<const Surface*(const SourceLink&)>
Delegate to unpack the surface associated with a source link.
-
template<typename external_spacepoint_t>
using SpacePointGrid = detail::Grid<std::vector<std::unique_ptr<InternalSpacePoint<external_spacepoint_t>>>, detail::Axis<detail::AxisType::Equidistant, detail::AxisBoundaryType::Closed>, detail::Axis<detail::AxisType::Variable, detail::AxisBoundaryType::Bound>>
-
using SquareMatrix2 = ActsSquareMatrix<2>
-
using SquareMatrix3 = ActsSquareMatrix<3>
-
using SquareMatrix4 = ActsSquareMatrix<4>
-
typedef std::tuple<std::shared_ptr<const Acts::Surface>, std::shared_ptr<const Acts::ISurfaceMaterial>, Acts::GeometryContext> SurfaceAndMaterialWithContext
-
typedef ObjectIntersection<Surface> SurfaceIntersection
Typedef of the surface intersection.
-
using SurfaceMatcher = std::function<bool(const GeometryContext &gctx, BinningValue, const Surface*, const Surface*)>
-
using surfaceMaterialPointer = const Acts::ISurfaceMaterial*
-
using SurfaceMatrix = std::vector<SurfaceVector>
-
typedef std::shared_ptr<const Surface> SurfacePtr
-
typedef std::vector<SurfacePtr> SurfacePtrVector
-
typedef std::vector<const Surface*> SurfaceVector
-
template<typename T>
using TrackAccessor = TrackAccessorBase<T, false>
-
using TrackIndexType = std::uint32_t
-
typedef std::pair<const Acts::TrackingVolume*, std::shared_ptr<const Acts::IVolumeMaterial>> TrackingVolumeAndMaterial
-
typedef BinnedArray<TrackingVolumePtr> TrackingVolumeArray
A BinnedArray of a std::shared_tr to a TrackingVolume.
-
using TrackingVolumeBoundaries = std::vector<TrackingVolumeBoundaryPtr>
-
using TrackingVolumeBoundaryPtr = std::shared_ptr<const BoundarySurfaceT<TrackingVolume>>
-
using TrackingVolumeOrderPosition = std::pair<TrackingVolumePtr, Vector3>
-
using TrackingVolumePointer = const Acts::TrackingVolume*
-
typedef std::shared_ptr<const TrackingVolume> TrackingVolumePtr
A std::shared_ptr to a tracking volume.
-
typedef std::vector<TrackingVolumePtr> TrackingVolumeVector
A std::vector of a std::shared_ptr to a TrackingVolume.
-
using Transform2 = Eigen::Transform<ActsScalar, 2, Eigen::AffineCompact>
-
using Transform3 = Eigen::Transform<ActsScalar, 3, Eigen::Affine>
-
using Translation2 = Eigen::Translation<ActsScalar, 2>
-
using Translation3 = Eigen::Translation<ActsScalar, 3>
-
using V3Matrix = std::vector<V3Vector>
-
using V3Vector = std::vector<Vector3>
-
using VariantCovariance = std::variant<BoundSquareMatrix, FreeSquareMatrix>
-
template<typename indices_t>
using VariantMeasurement = typename detail::VariantMeasurementGenerator<indices_t, detail::kParametersSize<indices_t>>::Type Variant that can contain all possible measurements in a parameter space.
- Template Parameters
indices_t – Parameter index type, determines the full parameter space
-
using VariantTransportJacobian = std::variant<BoundMatrix, BoundToFreeMatrix, FreeToBoundMatrix, FreeMatrix>
-
using Vector2 = ActsVector<2>
-
using Vector3 = ActsVector<3>
-
using Vector4 = ActsVector<4>
-
typedef std::shared_ptr<const VolumeBounds> VolumeBoundsPtr
-
using volumeMaterialPointer = const Acts::IVolumeMaterial*
Enums
-
enum AlignmentIndices
Components of alignment parameters vector.
To be used to access components by named indices instead of just numbers. This must be a regular
enumand not a scopedenum classto allow implicit conversion to an integer. The enum value are thus visible directly innamespace Actsand are prefixed to avoid naming collisions.Values:
-
enumerator eAlignmentCenter0
-
enumerator eAlignmentCenter1
-
enumerator eAlignmentCenter2
-
enumerator eAlignmentRotation0
-
enumerator eAlignmentRotation1
-
enumerator eAlignmentRotation2
-
enumerator eAlignmentSize
-
enumerator eAlignmentCenter0
-
enum BinningOption
flag for open/closed bins
Values:
-
enumerator open
-
enumerator closed
-
enumerator open
-
enum BinningType
, BinningOption & BinningAccess
BinningType:
Enumeration to qualify the binning type for the use of the LayerArrayCreator and the TrackingVolumeArrayCreator
BinningOption: open: [0,max] closed: 0 -> nextbin -> max -> 0
BinningValue necessary access to global positions
Values:
-
enumerator equidistant
-
enumerator arbitrary
-
enum BinningValue
how to take the global / local position
Values:
-
enumerator binX
-
enumerator binY
-
enumerator binZ
-
enumerator binR
-
enumerator binPhi
-
enumerator binRPhi
-
enumerator binH
-
enumerator binEta
-
enumerator binMag
-
enumerator binValues
-
enumerator binX
-
enum BoundarySurfaceFace
Enum to describe the position of the BoundarySurface respectively to the frame orientatin of the volume, this is mainly meant for code readability.
The different numeration sequences can be found in the documentation of the actual VolumeBounds implementations.
The order of faces is chosen to follow - as much as possible - a circular structure.
Values:
-
enumerator negativeFaceXY
-
enumerator positiveFaceXY
-
enumerator negativeFaceYZ
-
enumerator positiveFaceYZ
-
enumerator negativeFaceZX
-
enumerator positiveFaceZX
-
enumerator cylinderCover
-
enumerator tubeInnerCover
-
enumerator tubeOuterCover
-
enumerator tubeSectorNegativePhi
-
enumerator tubeSectorPositivePhi
-
enumerator tubeSectorInnerCover
-
enumerator tubeSectorOuterCover
-
enumerator trapezoidFaceAlpha
-
enumerator trapezoidFaceBeta
-
enumerator index0
-
enumerator index1
-
enumerator index2
-
enumerator index3
-
enumerator index4
-
enumerator index5
-
enumerator index6
-
enumerator index7
-
enumerator index8
-
enumerator index9
-
enumerator index10
-
enumerator index11
-
enumerator undefinedFace
-
enumerator negativeFaceXY
-
enum BoundIndices
Components of a bound track parameters vector.
To be used to access components by named indices instead of just numbers. This must be a regular
enumand not a scopedenum classto allow implicit conversion to an integer. The enum value are thus visible directly innamespace Actsand are prefixed to avoid naming collisions.Values:
-
enumerator eBoundLoc0
-
enumerator eBoundLoc1
-
enumerator eBoundPhi
-
enumerator eBoundTheta
-
enumerator eBoundQOverP
-
enumerator eBoundTime
-
enumerator eBoundSize
-
enumerator eBoundLoc0
-
enum class CombinatorialKalmanFilterError
Values:
-
enumerator UpdateFailed
-
enumerator SmoothFailed
-
enumerator OutputConversionFailed
-
enumerator MeasurementSelectionFailed
-
enumerator PropagationReachesMaxSteps
-
enumerator UpdateFailed
-
enum CoordinateIndices
Components of coordinate vectors.
To be used to access coordinate components by named indices instead of magic numbers. This must be a regular
enumand not a scopedenum classto allow implicit conversion to an integer. The enum value are thus visible directly innamespace Acts.This index enum is not user-configurable (in contrast e.g. to the track parameter index enums) since it must be compatible with varying dimensionality (2d-4d) and other access methods (
.{x,y,z}()accessors).Values:
-
enumerator ePos0
-
enumerator ePos1
-
enumerator ePos2
-
enumerator eTime
-
enumerator eMom0
-
enumerator eMom1
-
enumerator eMom2
-
enumerator eEnergy
-
enumerator eX
-
enumerator eY
-
enumerator eZ
-
enumerator ePos0
-
enum class DelegateType
Ownership enum for
Delegate.Values:
-
enumerator Owning
-
enumerator NonOwning
-
enumerator Owning
-
enum class DetectorMeasurementInfo : short
Values:
-
enumerator eDefault
-
enumerator eDetailed
-
enumerator eDefault
-
enum class EigenStepperError
Values:
-
enumerator StepSizeStalled
-
enumerator StepInvalid
-
enumerator StepSizeAdjustmentFailed
-
enumerator StepSizeStalled
-
enum FreeIndices
Components of a free track parameters vector.
To be used to access components by named indices instead of just numbers. This must be a regular
enumand not a scopedenum classto allow implicit conversion to an integer. The enum value are thus visible directly innamespace Actsand are prefixed to avoid naming collisions.Values:
-
enumerator eFreePos0
-
enumerator eFreePos1
-
enumerator eFreePos2
-
enumerator eFreeTime
-
enumerator eFreeDir0
-
enumerator eFreeDir1
-
enumerator eFreeDir2
-
enumerator eFreeQOverP
-
enumerator eFreeSize
-
enumerator eFreePos0
-
enum class IntersectionStatus : int
Status enum.
Values:
-
enumerator missed
-
enumerator unreachable
-
enumerator reachable
-
enumerator onSurface
-
enumerator missed
-
enum class KalmanFitterError
Values:
-
enumerator ForwardUpdateFailed
-
enumerator BackwardUpdateFailed
-
enumerator SmoothFailed
-
enumerator OutputConversionFailed
-
enumerator NoMeasurementFound
-
enumerator ForwardUpdateFailed
-
enum LayerType
For code readability, it distinguishes between different type of layers, which steers the behaviour in the navigation.
Values:
-
enumerator passive
-
enumerator active
-
enumerator passive
-
enum LinIndices
Enum to access the components of a track parameter vector.
Here, we parametrize the track via a 4D point on the track, the momentum angles of the particle at that point, and q/p or 1/p.
Note
It would make sense to rename these parameters if they are used outside of track linearization.
Note
This must be a regular
enumand not a scopedenum classto allow implicit conversion to an integer. The enum value are thus visible directly innamespace Actsand are prefixed to avoid naming collisions.Values:
-
enumerator eLinPos0
-
enumerator eLinPos1
-
enumerator eLinPos2
-
enumerator eLinTime
-
enumerator eLinPhi
-
enumerator eLinTheta
-
enumerator eLinQOverP
-
enumerator eLinSize
-
enumerator eLinPosSize
-
enumerator eLinMomSize
-
enumerator eLinPos0
-
enum class MagneticFieldError
Values:
-
enumerator OutOfBounds
-
enumerator OutOfBounds
-
enum MappingType
This enum describes the type of surface material mapping.
Values:
-
enumerator PreMapping
-
enumerator Default
-
enumerator PostMapping
-
enumerator Sensor
-
enumerator PreMapping
-
enum class MaterialUpdateStage : int
This is a steering enum to tell which material update stage:
PreUpdate : update on approach of a surface
FullUpdate : update when passing a surface
PostUpdate : update when leaving a surface
Values:
-
enumerator PreUpdate
-
enumerator FullUpdate
-
enumerator PostUpdate
-
enum class MixtureReductionMethod
Available reduction methods for the reduction of a Gaussian mixture.
Values:
-
enumerator eMean
-
enumerator eMaxWeight
-
enumerator eMean
-
enum class MultiStepperError
Values:
-
enumerator ComponentNotOnSurface
-
enumerator StateOfMultipleComponentsRequested
-
enumerator AverageTrackLeftCurrentVolume
-
enumerator AllComponentsSteppingError
-
enumerator AllComponentsConversionToBoundFailed
-
enumerator SomeComponentsConversionToBoundFailed
-
enumerator ComponentNotOnSurface
-
enum NoiseUpdateMode
to tell how to deal with noise term in covariance transport
removeNoise: subtract noise term
addNoise: add noise term
Values:
-
enumerator removeNoise
-
enumerator addNoise
-
enum PdgParticle
Symbolic values for commonly used PDG particle numbers.
Values:
-
enumerator eInvalid
-
enumerator eElectron
-
enumerator eAntiElectron
-
enumerator ePositron
-
enumerator eMuon
-
enumerator eAntiMuon
-
enumerator eTau
-
enumerator eAntiTau
-
enumerator eGamma
-
enumerator ePionZero
-
enumerator ePionPlus
-
enumerator ePionMinus
-
enumerator eNeutron
-
enumerator eAntiNeutron
-
enumerator eProton
-
enumerator eAntiProton
-
enumerator eLead
-
enumerator eInvalid
-
enum class PropagatorError
Values:
-
enumerator Failure
-
enumerator WrongDirection
-
enumerator StepCountLimitReached
-
enumerator Failure
-
enum class SpacePointCandidateType : short
Values:
-
enumerator eBottom
-
enumerator eTop
-
enumerator eBottom
-
enum class SurfaceError
Values:
-
enumerator GlobalPositionNotOnSurface
-
enumerator GlobalPositionNotOnSurface
-
enum TrackStateFlag
This enum describes the type of TrackState.
Values:
-
enumerator MeasurementFlag
-
enumerator ParameterFlag
-
enumerator OutlierFlag
-
enumerator HoleFlag
-
enumerator MaterialFlag
-
enumerator NumTrackStateFlags
-
enumerator MeasurementFlag
-
enum class TrackStatePropMask : std::uint8_t
Collection of bit masks to enable steering which components of a track state should be initialized, and which should be left invalid.
These mask values can be combined using binary operators, so (TrackStatePropMask::Predicted | TrackStatePropMask::Jacobian) will instruct allocating storage for both predicted parameters (including covariance) and a jacobian. The enum is used as a strong type wrapper around the bits to prevent autoconversion from integer
Values:
-
enumerator None
-
enumerator Predicted
-
enumerator Filtered
-
enumerator Smoothed
-
enumerator Jacobian
-
enumerator Calibrated
-
enumerator All
-
enumerator None
-
enum class VertexingError
Values:
-
enumerator NumericFailure
-
enumerator EmptyInput
-
enumerator SeedingError
-
enumerator NotConverged
-
enumerator ElementNotFound
-
enumerator NoCovariance
-
enumerator NumericFailure
-
enum WrappingCondition
Values:
-
enumerator Undefined
inconsistency detected
-
enumerator Attaching
attach the volumes
-
enumerator Inserting
insert the new volume
-
enumerator Wrapping
wrap the new volume around
-
enumerator CentralInserting
insert the new one into the center
-
enumerator CentralWrapping
wrap the new central volume around
-
enumerator NoWrapping
no inner volume present - no wrapping needed
-
enumerator Undefined
Functions
-
ACTS_STATIC_CHECK_CONCEPT(ChargeConcept, AnyCharge)
-
ACTS_STATIC_CHECK_CONCEPT(ChargeConcept, Neutral)
-
ACTS_STATIC_CHECK_CONCEPT(ChargeConcept, NonNeutralCharge)
-
ACTS_STATIC_CHECK_CONCEPT(ChargeConcept, SinglyCharged)
-
ACTS_STATIC_CHECK_CONCEPT(ConstMultiTrajectoryBackend, ConstVectorMultiTrajectory)
-
ACTS_STATIC_CHECK_CONCEPT(ConstTrackContainerBackend, ConstVectorTrackContainer)
-
ACTS_STATIC_CHECK_CONCEPT(MutableMultiTrajectoryBackend, VectorMultiTrajectory)
-
ACTS_STATIC_CHECK_CONCEPT(TrackContainerBackend, VectorTrackContainer)
-
void addCylinderLayerProtoMaterial(dd4hep::DetElement detElement, Layer &cylinderLayer, const Logger &logger = getDummyLogger())
Helper method to translate DD4hep material to Acts::ISurfaceMaterial.
This is used to assign proto material to Cylinder Layers
- Parameters
detElement – the DD4hep detector element for which this material is assigned
cylinderLayer – is the target layer
logger – a
Loggerfor output
-
void addDiscLayerProtoMaterial(dd4hep::DetElement detElement, Layer &discLayer, const Logger &logger = getDummyLogger())
Helper method to translate DD4hep material to Acts::ISurfaceMaterial.
Thisis used to assign proto material to Disc Layers
- Parameters
detElement – the DD4hep detector element for which this material is assigned
discLayer – is the target layer
logger – a
Loggerfor output
-
void addLayerProtoMaterial(const dd4hep::rec::VariantParameters ¶ms, Layer &layer, const std::vector<std::pair<const std::string, Acts::BinningOption>> &binning, const Logger &logger = getDummyLogger())
Helper method to be called for Cylinder and Disc Proto material.
For both, cylinder and disc, the closed binning value is “binPhi”
- Parameters
params – An instance of
DD4hep::VariantParameterslayer – the Layer to assign the proto material
binning – the Binning prescription for the ActsExtension
logger – a
Loggerfor output
-
BinUtility adjustBinUtility(const BinUtility &bu, const CuboidVolumeBounds &cBounds, const Transform3 &transform)
adjust the BinUtility bu to the dimensions of cuboid volume bounds
- Parameters
bu – BinUtility at source
cBounds – the Cuboid volume bounds to adjust to
transform – Transform for the adjusted
BinUtility
- Returns
new updated BinUtiltiy
-
BinUtility adjustBinUtility(const BinUtility &bu, const CutoutCylinderVolumeBounds &cBounds, const Transform3 &transform)
adjust the BinUtility bu to the dimensions of cutout cylinder volume bounds
- Parameters
bu – BinUtility at source
cBounds – the Cutout Cylinder volume bounds to adjust to
transform – Transform for the adjusted
BinUtility
- Returns
new updated BinUtiltiy
-
BinUtility adjustBinUtility(const BinUtility &bu, const CylinderBounds &cBounds, const Transform3 &transform)
adjust the BinUtility bu to the dimensions of cylinder bounds
- Parameters
bu – BinUtility at source
cBounds – the Cylinder bounds to adjust to
transform – Transform for the adjusted
BinUtility
- Returns
new updated BinUtiltiy
-
BinUtility adjustBinUtility(const BinUtility &bu, const CylinderVolumeBounds &cBounds, const Transform3 &transform)
adjust the BinUtility bu to the dimensions of cylinder volume bounds
- Parameters
bu – BinUtility at source
cBounds – the Cylinder volume bounds to adjust to
transform – Transform for the adjusted
BinUtility
- Returns
new updated BinUtiltiy
-
BinUtility adjustBinUtility(const BinUtility &bu, const RadialBounds &rBounds, const Transform3 &transform)
adjust the BinUtility bu to the dimensions of radial bounds
- Parameters
bu – BinUtility at source
rBounds – the Radial bounds to adjust to
transform – Transform for the adjusted
BinUtility
- Returns
new updated BinUtiltiy
-
BinUtility adjustBinUtility(const BinUtility &bu, const RectangleBounds &pBounds, const Transform3 &transform)
adjust the BinUtility bu to the dimensions of plane bounds
- Parameters
bu – BinUtility at source
pBounds – the Rectangle bounds to adjust to
transform – Transform for the adjusted
BinUtility
- Returns
new updated BinUtiltiy
-
BinUtility adjustBinUtility(const BinUtility &bu, const Surface &surface, const GeometryContext &gctx)
adjust the BinUtility bu to a surface
- Parameters
bu – BinUtility at source
surface – Surface to which the adjustment is being done
gctx – Geometry context to get the surfaces transform
- Returns
new updated BinUtiltiy
-
BinUtility adjustBinUtility(const BinUtility &bu, const TrapezoidBounds &pBounds, const Transform3 &transform)
adjust the BinUtility bu to the dimensions of plane bounds
- Parameters
bu – BinUtility at source
pBounds – the Trapezoid bounds to adjust to
transform – Transform for the adjusted
BinUtility
- Returns
new updated BinUtiltiy
-
BinUtility adjustBinUtility(const BinUtility &bu, const Volume &volume)
adjust the BinUtility bu to a volume
- Parameters
bu – BinUtility at source
volume – Volume to which the adjustment is being done
- Returns
new updated BinUtiltiy
-
inline const std::vector<std::string> &binningValueNames()
screen output option
-
template<typename MatrixType>
MatrixType bitsetToMatrix(const std::bitset<MatrixType::RowsAtCompileTime * MatrixType::ColsAtCompileTime> bs) Convert a bitset to a matrix of integers, with each element set to the bit value.
Note
How the bits are assigned to matrix elements depends on the storage type of the matrix being converted (row-major or col-major)
- Template Parameters
MatrixType – Matrix type that is produced
- Parameters
bs – The bitset to convert
- Returns
A matrix with the integer values of the bits from
bs
-
template<typename A, typename B>
inline ActsMatrix<A::RowsAtCompileTime, B::ColsAtCompileTime> blockedMult(const A &a, const B &b) Perform a blocked matrix multiplication, avoiding Eigen GEMM methods.
- Template Parameters
A – The type of the first matrix, which should be MxN
B – The type of the second matrix, which should be NxP
- Parameters
a – [in] An MxN matrix of type A
b – [in] An NxP matrix of type P
- Returns
The product ab
-
template<typename track_container_t, typename track_state_container_t, template<typename> class holder_t>
void calculateTrackQuantities(Acts::TrackProxy<track_container_t, track_state_container_t, holder_t, false> track) Helper function to calculate a number of track level quantities and store them on the track itself.
Note
The input track needs to be mutable, so
ReadOnly=false- Template Parameters
track_container_t – the track container backend
track_state_container_t – the track state container backend
holder_t – the holder type for the track container backends
- Parameters
track – A mutable track proxy to operate on
-
template<typename T, typename U>
T clampValue(U value) Clamp a numeric value to another type, respecting range of the target type.
- Template Parameters
T – the target type
U – the source type
- Parameters
value – the value to clamp
- Returns
the clamped value
-
void collectCompounds_dd4hep(dd4hep::DetElement &detElement, std::vector<dd4hep::DetElement> &compounds)
Method internally used by convertDD4hepDetector to collect all volumes of a compound detector.
- Parameters
detElement – [in] the dd4hep::DetElement of the volume of which the compounds should be collected
compounds – [out] the DD4hep::DetElements of the compounds contained by detElement
-
void collectLayers_dd4hep(dd4hep::DetElement &detElement, std::vector<dd4hep::DetElement> &layers, const Logger &logger)
Method internally used by convertDD4hepDetector.
- Parameters
detElement – [in] the dd4hep::DetElement of the volume of which the layers should be collected
layers – [out] the DD4hep::DetElements of the layers contained by detElement
logger – a
Loggerfor output
-
void collectSubDetectors_dd4hep(dd4hep::DetElement &detElement, std::vector<dd4hep::DetElement> &subdetectors, const Logger &logger)
Method internally used by convertDD4hepDetector to collect all sub detectors Sub detector means each ‘compound’ DetElement or DetElements which are declared as ‘isBarrel’ or ‘isBeampipe’ by their extension.
- Parameters
detElement – [in] the dd4hep::DetElement of the volume of which the sub detectors should be collected
subdetectors – [out] the DD4hep::DetElements of the sub detectors contained by detElement
logger – a
Loggerfor output
-
float computeEnergyLossBethe(const MaterialSlab &slab, float m, float qOverP, float absQ)
Compute the mean energy loss due to ionisation and excitation.
This computes the mean energy loss -dE(x) through a material with the given properties, i.e. it computes
where -dE/dx is given by the Bethe formula. The computations are valid for intermediate particle energies.-dE(x) = -dE/dx * x
- Parameters
slab – The traversed material and its properties
m – Particle mass
qOverP – Particle charge divided by absolute momentum
absQ – Absolute particle charge
-
float computeEnergyLossLandau(const MaterialSlab &slab, float m, float qOverP, float absQ)
Compute the most propable energy loss due to ionisation and excitation.
Compute the mean energy loss due to ionisation and excitation.
This computes the mean energy loss -dE(x) through a material with the given properties, i.e. it computes
where -dE/dx is given by the Bethe formula. The computations are valid for intermediate particle energies.-dE(x) = -dE/dx * x
This computes the most probable energy loss -dE(x) through a material of the given properties and thickness as described by the mode of the Landau-Vavilov-Bichsel distribution. The computations are valid for intermediate particle energies.
- Parameters
slab – The traversed material and its properties
m – Particle mass
qOverP – Particle charge divided by absolute momentum
absQ – Absolute particle charge
-
float computeEnergyLossLandauFwhm(const MaterialSlab &slab, float m, float qOverP, float absQ)
Compute the full with half maximum of landau energy loss distribution.
See also
computeEnergyLossBethe for parameters description
-
float computeEnergyLossLandauSigma(const MaterialSlab &slab, float m, float qOverP, float absQ)
Compute the Gaussian-equivalent sigma for the ionisation loss fluctuations.
This is the sigma parameter of a Gaussian distribution with the same full-width-half-maximum as the Landau-Vavilov-Bichsel distribution. The computations are valid for intermediate particle energies.
See also
computeEnergyLossBethe for parameters description
-
float computeEnergyLossLandauSigmaQOverP(const MaterialSlab &slab, float m, float qOverP, float absQ)
Compute q/p Gaussian-equivalent sigma due to ionisation loss fluctuations.
Compute the mean energy loss due to ionisation and excitation.
This computes the mean energy loss -dE(x) through a material with the given properties, i.e. it computes
where -dE/dx is given by the Bethe formula. The computations are valid for intermediate particle energies.-dE(x) = -dE/dx * x
- Parameters
slab – The traversed material and its properties
m – Particle mass
qOverP – Particle charge divided by absolute momentum
absQ – Absolute particle charge
-
float computeEnergyLossMean(const MaterialSlab &slab, PdgParticle absPdg, float m, float qOverP, float absQ)
Compute the combined mean energy loss.
This computes the combined mean energy loss -dE(x) including ionisation and radiative effects. The computations are valid over a wide range of particle energies.
- Parameters
slab – The traversed material and its properties
absPdg – Absolute particle type PDG identifier
m – Particle mass
qOverP – Particle charge divided by absolute momentum
absQ – Absolute particle charge
-
float computeEnergyLossMode(const MaterialSlab &slab, PdgParticle absPdg, float m, float qOverP, float absQ)
Compute the combined most probably energy loss.
Compute the combined mean energy loss.
This computes the combined mean energy loss -dE(x) including ionisation and radiative effects. The computations are valid over a wide range of particle energies.
- Parameters
slab – The traversed material and its properties
absPdg – Absolute particle type PDG identifier
m – Particle mass
qOverP – Particle charge divided by absolute momentum
absQ – Absolute particle charge
-
float computeEnergyLossRadiative(const MaterialSlab &slab, PdgParticle absPdg, float m, float qOverP, float absQ)
Compute the mean energy loss due to radiative effects at high energies.
This computes the mean energy loss -dE(x) using an approximative formula. Bremsstrahlung is always included; direct e+e- pair production and photo-nuclear interactions only for muons.
- Parameters
slab – The traversed material and its properties
absPdg – Absolute particle type PDG identifier
m – Particle mass
qOverP – Particle charge divided by absolute momentum
absQ – Absolute particle charge
-
float computeMultipleScatteringTheta0(const MaterialSlab &slab, PdgParticle absPdg, float m, float qOverP, float absQ)
Compute the core width of the projected planar scattering distribution.
- Parameters
slab – The traversed material and its properties
absPdg – Absolute particle type PDG identifier
m – Particle mass
qOverP – Particle charge divided by absolute momentum
absQ – Absolute particle charge
Global method which creates the TrackingGeometry from DD4hep input.
This method returns a std::unique_ptr of the TrackingGeometry from the World DD4hep DetElement.
- Attention
The default thickness should be set thin enough that no touching or overlapping with the next layer can happen.
Note
Possible binningtypes:
arbitrary - of the sizes if the surfaces and the distance in between vary. This mode finds out the bin boundaries by scanning through the surfaces.
equidistant - if the sensitive surfaces are placed equidistantly
Note
equidistant binningtype is recommended because it is faster not only while building the geometry but also for look up during the extrapolation
Note
Layers containing surfaces per default are not allowed to be attached to each other (navigation will fail at this point). However, to allow material layers (not containing surfaces) to be attached to each other, this default thickness is needed. In this way, the layer will be thin (with space to the next layer), but the material will have the’real’ thickness.
- Parameters
worldDetElement – [in] the DD4hep DetElement of the world
logger – [in] A logger instance geometry building
bTypePhi – [in] is how the sensitive surfaces (modules) should be binned in a layer in phi direction.
bTypeR – [in] is how the sensitive surfaces (modules) should be binned in a layer in r direction
bTypeZ – [in] is how the sensitive surfaces (modules) should be binned in a layer in z direction
layerEnvelopeR – [in] the tolerance added to the geometrical extension in r of the layers contained to build the volume envelope around
layerEnvelopeZ – [in] the tolerance added to the geometrical extension in z of the layers contained to build the volume envelope around
defaultLayerThickness – [in] In case no surfaces (to be contained by the layer) are handed over, the layer thickness will be set to this value
sortSubDetectors – [in]
std::functionwhich should be used in order to sort all sub detectors (=all Detelements collected by the methodcollectSubDetectors()) from bottom to top to ensure correct wrapping of the volumes, which is needed for navigation. Therefore the different hierarchies need to be sorted ascending. The default is sorting by ID.gctx – The geometry context to use
matDecorator – is the material decorator that loads material maps
geometryIdentifierHook – Hook to apply to surfaces during geometry closure.
- Throws
std::logic_error – if an error in the translation occurs
- Pre
Before using this method make sure, that the preconditions described in DD4hepPlugins are met.
- Returns
std::unique_ptr to the full TrackingGeometry
The Tracking geometry needs to be built from bottom to top to ensure Navigation. Therefore the different hierarchies need to be sorted ascending. Per default the sub detectors are sorted by the id of their dd4hep::DetElement. In case another sorting needs to be applied, the users can provide their own function
-
Grid2D createGrid(MaterialGridAxisData gridAxis1, MaterialGridAxisData gridAxis2)
Helper method that creates the cache grid for the mapping.
This grid allows the collection of material at a the anchor points.
Note
The data of the axes is given in the std::array as {minimum value, maximum value, number of bins}
- Parameters
gridAxis1 – [in] Axis data
gridAxis2 – [in] Axis data
- Returns
The grid
-
Grid3D createGrid(MaterialGridAxisData gridAxis1, MaterialGridAxisData gridAxis2, MaterialGridAxisData gridAxis3)
Helper method that creates the cache grid for the mapping.
This grid allows the collection of material at a the anchor points.
Note
The data of the axes is given in the std::array as {minimum value, maximum value, number of bins}
- Parameters
gridAxis1 – [in] Axis data
gridAxis2 – [in] Axis data
gridAxis3 – [in] Axis data
- Returns
The grid
-
Grid2D createGrid2D(const BinUtility &bins, std::function<Acts::Vector2(Acts::Vector3)> &transfoGlobalToLocal)
Create a 2DGrid using a BinUtility.
Also determine the corresponding global to local transform and grid mapping function
- Parameters
bins – [in] BinUtility of the volume to be mapped
transfoGlobalToLocal – [in] Global to local transform to be updated.
- Returns
the 3D grid
-
Grid3D createGrid3D(const BinUtility &bins, std::function<Acts::Vector3(Acts::Vector3)> &transfoGlobalToLocal)
Create a 3DGrid using a BinUtility.
Also determine the corresponding global to local transform and grid mapping function
- Parameters
bins – [in] BinUtility of the volume to be mapped
transfoGlobalToLocal – [in] Global to local transform to be updated.
- Returns
the 3D grid
-
std::shared_ptr<Acts::ProtoSurfaceMaterial> createProtoMaterial(const dd4hep::rec::VariantParameters ¶ms, const std::string &valueTag, const std::vector<std::pair<const std::string, Acts::BinningOption>> &binning, const Logger &logger = getDummyLogger())
Helper method to create proto material - to be called from the addProto(…) methods.
- Parameters
params – An instance of
DD4hep::VariantParametersvalueTag – the xml tag for to ActsExtension to be parsed
binning – the Binning prescription for the ActsExtension
logger – a
Loggerfor output
-
std::shared_ptr<const CylinderVolumeHelper> cylinderVolumeHelper_dd4hep(const Logger &logger)
Helper method internally used to create a default Acts::CylinderVolumeBuilder.
-
template<class T, class decorator_t>
void decorateJson([[maybe_unused]] const decorator_t *decorator, [[maybe_unused]] const T &src, [[maybe_unused]] nlohmann::json &dest)
-
template<class T, class decorator_t>
void decorateJson([[maybe_unused]] const decorator_t *decorator, [[maybe_unused]] const T *src, [[maybe_unused]] nlohmann::json &dest)
-
float deriveEnergyLossBetheQOverP(const MaterialSlab &slab, float m, float qOverP, float absQ)
Derivative of the Bethe energy loss with respect to q/p.
Compute the mean energy loss due to ionisation and excitation.
This computes the mean energy loss -dE(x) through a material with the given properties, i.e. it computes
where -dE/dx is given by the Bethe formula. The computations are valid for intermediate particle energies.-dE(x) = -dE/dx * x
- Parameters
slab – The traversed material and its properties
m – Particle mass
qOverP – Particle charge divided by absolute momentum
absQ – Absolute particle charge
-
float deriveEnergyLossLandauQOverP(const MaterialSlab &slab, float m, float qOverP, float absQ)
Derivative of the most probable ionisation energy loss with respect to q/p.
Compute the mean energy loss due to ionisation and excitation.
This computes the mean energy loss -dE(x) through a material with the given properties, i.e. it computes
where -dE/dx is given by the Bethe formula. The computations are valid for intermediate particle energies.-dE(x) = -dE/dx * x
- Parameters
slab – The traversed material and its properties
m – Particle mass
qOverP – Particle charge divided by absolute momentum
absQ – Absolute particle charge
-
float deriveEnergyLossMeanQOverP(const MaterialSlab &slab, PdgParticle absPdg, float m, float qOverP, float absQ)
Derivative of the combined mean energy loss with respect to q/p.
Compute the combined mean energy loss.
This computes the combined mean energy loss -dE(x) including ionisation and radiative effects. The computations are valid over a wide range of particle energies.
- Parameters
slab – The traversed material and its properties
absPdg – Absolute particle type PDG identifier
m – Particle mass
qOverP – Particle charge divided by absolute momentum
absQ – Absolute particle charge
-
float deriveEnergyLossModeQOverP(const MaterialSlab &slab, PdgParticle absPdg, float m, float qOverP, float absQ)
Derivative of the combined most probable energy loss with respect to q/p.
Compute the combined mean energy loss.
This computes the combined mean energy loss -dE(x) including ionisation and radiative effects. The computations are valid over a wide range of particle energies.
- Parameters
slab – The traversed material and its properties
absPdg – Absolute particle type PDG identifier
m – Particle mass
qOverP – Particle charge divided by absolute momentum
absQ – Absolute particle charge
-
float deriveEnergyLossRadiativeQOverP(const MaterialSlab &slab, PdgParticle absPdg, float m, float qOverP, float absQ)
Derivative of the mean radiative energy loss with respect to q/p.
Compute the mean energy loss due to radiative effects at high energies.
This computes the mean energy loss -dE(x) using an approximative formula. Bremsstrahlung is always included; direct e+e- pair production and photo-nuclear interactions only for muons.
- Parameters
slab – The traversed material and its properties
absPdg – Absolute particle type PDG identifier
m – Particle mass
qOverP – Particle charge divided by absolute momentum
absQ – Absolute particle charge
-
template<typename container_type, typename container_type_iter = decltype(std::begin(std::declval<container_type>())), typename = decltype(std::end(std::declval<container_type>()))>
constexpr auto enumerate(container_type &&iterable) Helper utility to allow indexed enumeration with structured binding.
Usage:
for (auto [ i, value ] = enumerate(container) ) { … };
with ‘container’ any stl-like container
-
template<typename spacepoint_iterator_t>
std::optional<BoundVector> estimateTrackParamsFromSeed(const GeometryContext &gctx, spacepoint_iterator_t spBegin, spacepoint_iterator_t spEnd, const Surface &surface, const Vector3 &bField, ActsScalar bFieldMin, const Acts::Logger &logger = getDummyLogger(), ActsScalar mass = 139.57018 * UnitConstants::MeV) Estimate the full track parameters from three space points.
This method is based on the conformal map transformation. It estimates the full bound track parameters, i.e. (loc0, loc1, phi, theta, q/p, t) at the bottom space point. The bottom space is assumed to be the first element in the range defined by the iterators. It must lie on the surface provided for the representation of the bound track parameters. The magnetic field (which might be along any direction) is also necessary for the momentum estimation.
It resembles the method used in ATLAS for the track parameters estimated from seed, i.e. the function InDet::SiTrackMaker_xk::getAtaPlane here: https://acode-browser.usatlas.bnl.gov/lxr/source/athena/InnerDetector/InDetRecTools/SiTrackMakerTool_xk/src/SiTrackMaker_xk.cxx
- Template Parameters
spacepoint_iterator_t – The type of space point iterator
- Parameters
gctx – is the geometry context
spBegin – is the begin iterator for the space points
spEnd – is the end iterator for the space points
surface – is the surface of the bottom space point. The estimated bound track parameters will be represented also at this surface
bField – is the magnetic field vector
bFieldMin – is the minimum magnetic field required to trigger the estimation of q/pt
logger – A logger instance
mass – is the estimated particle mass
- Returns
optional bound parameters
-
template<typename spacepoint_iterator_t>
std::optional<BoundVector> estimateTrackParamsFromSeed(spacepoint_iterator_t spBegin, spacepoint_iterator_t spEnd, const Logger &logger = getDummyLogger()) Estimate the track parameters on the xy plane from at least three space points.
It assumes the trajectory projection on the xy plane is a circle, i.e. the magnetic field is along global z-axis.
The method is based on V. Karimaki NIM A305 (1991) 187-191: https://doi.org/10.1016/0168-9002(91)90533-V
no weights are used in Karimaki’s fit; d0 is the distance of the point of closest approach to the origin, 1/R is the curvature, phi is the angle of the direction propagation (counter clockwise as positive) at the point of cloest approach.
- Template Parameters
spacepoint_iterator_t – The type of space point iterator
- Parameters
spBegin – is the begin iterator for the space points
spEnd – is the end iterator for the space points
logger – A logger instance
- Returns
optional bound track parameters with the estimated d0, phi and 1/R stored with the indices, eBoundLoc0, eBoundPhi and eBoundQOverP, respectively. The bound parameters with other indices are set to zero.
-
Acts::InterpolatedBFieldMap<Acts::detail::Grid<Acts::Vector2, Acts::detail::EquidistantAxis, Acts::detail::EquidistantAxis>> fieldMapRZ(const std::function<size_t(std::array<size_t, 2> binsRZ, std::array<size_t, 2> nBinsRZ)> &localToGlobalBin, std::vector<double> rPos, std::vector<double> zPos, std::vector<Acts::Vector2> bField, double lengthUnit = UnitConstants::mm, double BFieldUnit = UnitConstants::T, bool firstQuadrant = false)
Method to setup the FieldMap.
e.g.: we have small grid with the values: r={2,3}, z ={4,5}, the corresponding indices are i (belonging to r) and j (belonging to z), the globalIndex is M (belonging to the value of the magnetic field B(r,z)) and the field map is:
r
i
z
j
B(r,z)
M
2
0
4
0
2.323
0
2
0
5
1
2.334
1
3
1
4
0
2.325
2
3
1
5
1
2.331
3
In this case the function would look like:
[](std::array<size_t, 2> binsRZ, std::array<size_t, 2> nBinsRZ) { return (binsRZ.at(0) * nBinsRZ.at(1) + binsRZ.at(1)); }
Note
The values do not need to be sorted or unique (this will be done inside the function)
Note
The values do not need to be sorted or unique (this will be done inside the function)
Note
The function localToGlobalBin determines how the magnetic field was stored in the vector in respect to the grid values
Note
If
firstQuadrantis true will create a field that is symmetric for all quadrants. e.g. we have the grid values r={0,1} with BFieldValues={2,3} on the r axis. If the flag is set to true the r-axis grid values will be set to {-1,0,1} and the BFieldValues will be set to {3,2,3}.- Parameters
localToGlobalBin – Function mapping the local bins of r,z to the global bin of the map magnetic field value
rPos – [in] Values of the grid points in r
zPos – [in] Values of the grid points in z
bField – [in] The magnetic field values inr r and z for all given grid points stored in a vector
lengthUnit – [in] The unit of the grid points
BFieldUnit – [in] The unit of the magnetic field
firstQuadrant – [in] Flag if set to true indicating that only the first quadrant of the grid points and the BField values has been given.
- Returns
A field map instance for use in interpolation.
-
Acts::InterpolatedBFieldMap<Acts::detail::Grid<Acts::Vector3, Acts::detail::EquidistantAxis, Acts::detail::EquidistantAxis, Acts::detail::EquidistantAxis>> fieldMapXYZ(const std::function<size_t(std::array<size_t, 3> binsXYZ, std::array<size_t, 3> nBinsXYZ)> &localToGlobalBin, std::vector<double> xPos, std::vector<double> yPos, std::vector<double> zPos, std::vector<Acts::Vector3> bField, double lengthUnit = UnitConstants::mm, double BFieldUnit = UnitConstants::T, bool firstOctant = false)
Method to setup the FieldMap.
e.g.: we have small grid with the values: x={2,3}, y={3,4}, z ={4,5}, the corresponding indices are i (belonging to x), j (belonging to y) and k (belonging to z), the globalIndex is M (belonging to the value of the magnetic field B(x,y,z)) and the field map is:
x
i
y
j
z
k
B(x,y,z)
M
2
0
3
0
4
0
2.323
0
2
0
3
0
5
1
2.334
1
2
0
4
1
4
0
2.325
2
2
0
4
1
5
1
2.331
3
3
1
3
0
4
0
2.323
4
3
1
3
0
5
1
2.334
5
3
1
4
1
4
0
2.325
6
3
1
4
1
5
1
2.331
7
In this case the function would look like:
[](std::array<size_t, 3> binsXYZ, std::array<size_t, 3> nBinsXYZ) { return (binsXYZ.at(0) * (nBinsXYZ.at(1) * nBinsXYZ.at(2)) + binsXYZ.at(1) * nBinsXYZ.at(2) + binsXYZ.at(2)); }
Note
The grid point values
xPos,yPosandzPosdo not need to be sorted or unique (this will be done inside the function)Note
The function
localToGlobalBindetermines how the magnetic field was stored in the vector in respect to the grid valuesNote
If
firstOctantis true, the function will assume a symmetrical field for all quadrants. e.g. we have the grid values z={0,1} with BFieldValues={2,3} on the r axis. If the flag is set to true the z-axis grid values will be set to {-1,0,1} and the BFieldValues will be set to {3,2,3}.- Parameters
localToGlobalBin – Function mapping the local bins of x,y,z to the global bin of the map magnetic field value
xPos – [in] Values of the grid points in x
yPos – [in] Values of the grid points in y
zPos – [in] Values of the grid points in z
bField – [in] The magnetic field values inr r and z for all given grid points stored in a vector
lengthUnit – [in] The unit of the grid points
BFieldUnit – [in] The unit of the magnetic field
firstOctant – [in] Flag if set to true indicating that only the first octant of the grid points and the BField values has been given.
- Returns
A field map instance for use in interpolation.
-
std::optional<float> findCharge(PdgParticle pdg)
Find the charge for a given PDG particle number.
- Returns
Charge in native units.
-
std::optional<float> findMass(PdgParticle pdg)
Find the mass for a given PDG particle number.
- Returns
Mass in native units.
-
std::optional<std::string_view> findName(PdgParticle pdg)
Find a descriptive particle name for a given PDG particle number.
- Returns
Particle name.
-
std::optional<ParticleData> findParticleData(PdgParticle pdg)
Find all known particle data for a given PDG particle number.
- Returns
Particle name.
-
void from_json(const nlohmann::json &j, BinningData &bd)
-
void from_json(const nlohmann::json &j, BinUtility &bu)
-
void from_json(const nlohmann::json &j, Extent &e)
-
void from_json(const nlohmann::json &j, Material &t)
-
void from_json(const nlohmann::json &j, MaterialSlab &t)
-
void from_json(const nlohmann::json &j, MaterialSlabMatrix &t)
-
void from_json(const nlohmann::json &j, ProtoDetector &pd)
-
void from_json(const nlohmann::json &j, ProtoVolume &pv)
-
void from_json(const nlohmann::json &j, surfaceMaterialPointer &material)
-
void from_json(const nlohmann::json &j, Transform3 &t)
-
void from_json(const nlohmann::json &j, volumeMaterialPointer &material)
-
std::unique_ptr<const Logger> getDefaultLogger(const std::string &name, const Logging::Level &lvl, std::ostream *log_stream = &std::cout)
get default debug output logger
This function returns a pointer to a Logger instance with the following decorations enabled:
time stamps
name of logging instance
debug level
- Parameters
name – [in] name of the logger instance
lvl – [in] debug threshold level
log_stream – [in] output stream used for printing debug messages
- Returns
pointer to logging instance
-
const Logger &getDummyLogger()
-
template<typename T>
T getParam(const std::string &key, dd4hep::DetElement &elt) Helper function to extract a parameter value from a dd4hep detector element from VariantParameters.
- Template Parameters
T – The value type
- Parameters
key – The key of the value to extract
elt – The detector element instance
- Returns
A copy of the value contained in the params instance
-
template<typename T>
T getParamOr(const std::string &key, const dd4hep::DetElement &elt, T alternative) Get a parameter value or an alternative value if either the VariantParameters extension isn’t set, or it doesn’t contain the demanded key.
- Template Parameters
T – The value type
- Parameters
key – The key of the value to extract
elt – The detector element instance
alternative – The value to return if no params are set of the key doesn’t exist
- Returns
The value behind key, or
alternative
-
inline const dd4hep::rec::VariantParameters &getParams(const dd4hep::DetElement &elt)
Helper function to extract a VariantParameters instance, const version.
- Parameters
elt – The detector element instance
- Returns
The VariantParameters instance
-
inline dd4hep::rec::VariantParameters &getParams(dd4hep::DetElement &elt)
Helper function to extract a VariantParameters instance.
- Parameters
elt – The detector element instance
- Returns
The VariantParameters instance
-
std::function<double(Acts::Vector3)> globalToLocalFromBin(Acts::BinningValue &type)
return a function that return the coordinate corresponding to type of bin
- Parameters
type – [in] Type of bin
- Returns
a coordinate transform function
-
constexpr HashedString hashString(std::string_view s)
-
inline bool hasParam(const std::string &key, dd4hep::DetElement &elt)
Check if a detector element has a key set in its VariantParameters.
- Parameters
key – The key to check existence for
elt – The detector element instance
- Returns
True if the element has VariantParameters and the key exists, false if either of these is not true
-
inline bool hasParams(dd4hep::DetElement &elt)
Check if a detector element has VariantParameters set.
- Parameters
elt – The detector element instance
- Returns
True if the VariantParameters exist, false if not
-
template<typename T, size_t N, class Point1, class Point2 = Point1, class Point3 = Point2, typename = std::enable_if_t<detail::can_interpolate<Point1, Point2, Point3, T>::value>>
inline T interpolate(const Point1 &position, const Point2 &lowerCorner, const Point3 &upperCorner, const std::array<T, N> &values) performs linear interpolation inside a hyper box
Note
Given
UandVof value typeTas well as twodoubleaandb, then the following must be a valid expressiona * U + b * Vyielding an object which is (implicitly) convertible toT.All
Pointtypes must represent d-dimensional positions and support coordinate access usingoperator[] which should return adouble(or a value which is implicitly convertible). Coordinate indices must start at 0.Nis the number of hyper box corners which is \(2^d\) where \(d\) is the dimensionality of the hyper box. The dimensionality must be consistent with the providedPointtypes.Definition of the canonical order for sorting the field values: The hyper box corners are numbered according to the following scheme. Each corner is defined by the set of lower/upper boundary limits in each dimension
i. This can be represented by a binary code (from left to right) where a0stands for a lower bound along this axis and a1stand for the upper bound along this axis. The left most bit corresponds to the first dimension and the bits to the left correspond to the 2nd, 3rd… dimension. The binary code can be interpreted as integer which gives the number of the corresponding hyper box corner. The field values are ordered according to ascending hyper box corner numbers.
As an example assume we have a 3D box with
lowerCorner= (1,2,3) andupperCorner= (4,5,6). The eight corners with their bit patterns and corner numbers are:(1,2,3): 000 = 0
(1,2,6): 001 = 1
(1,5,3): 010 = 2
(1,5,6): 011 = 3
(4,2,3): 100 = 4
(4,2,6): 101 = 5
(4,5,3): 110 = 6
(4,5,6): 111 = 7
- Template Parameters
T – type of values to be interpolated
N – number of hyper box corners
Point1 – type specifying geometric positions
Point2 – type specifying geometric positions
Point3 – type specifying geometric positions
- Parameters
position – [in] position to which to interpolate
lowerCorner – [in] generalized lower-left corner of hyper box (containing the minima of the hyper box along each dimension)
upperCorner – [in] generalized upper-right corner of hyper box (containing the maxima of the hyper box along each dimension)
values – [in] field values at the hyper box corners sorted in the canonical order defined below.
- Returns
interpolated value at given position
- Pre
positionmust describe a position inside the given hyper box, that is \(\text{lowerCorner}[i] \le \text{position}[i] \le \text{upperCorner}[i] \quad \forall i=0, \dots, d-1\).
-
std::error_code make_error_code(Acts::CombinatorialKalmanFilterError e)
-
std::error_code make_error_code(Acts::KalmanFitterError e)
-
std::error_code make_error_code(Acts::MagneticFieldError e)
-
std::error_code make_error_code(Acts::MultiStepperError e)
-
std::error_code make_error_code(Acts::PropagatorError e)
-
std::error_code make_error_code(Acts::SurfaceError e)
-
std::error_code make_error_code(Acts::VertexingError e)
-
std::error_code make_error_code(EigenStepperError e)
-
template<typename box_t>
box_t *make_octree(std::vector<std::unique_ptr<box_t>> &store, const std::vector<box_t*> &prims, size_t max_depth = 1, typename box_t::value_type envelope1 = 0) Build an octree from a list of bounding boxes.
Note
storeandprimsdo not need to contain the same objects.storeis only used to pass ownership back to the caller while preserving memory location.- Template Parameters
box_t – Works will all box types.
- Parameters
store – Owns the created boxes by means of
std::unique_ptr.prims – Boxes to store. This is a read only vector.
max_depth – No subdivisions beyond this level.
envelope1 – Envelope to add/subtract to dimensions in all directions.
- Returns
Pointer to the top most bounding box, containing the entire octree
-
static inline constexpr PdgParticle makeAbsolutePdgParticle(PdgParticle pdg)
Convert an anti-particle to its particle and leave particles as-is.
-
template<typename InputVector>
inline auto makeCurvilinearUnitU(const Eigen::MatrixBase<InputVector> &direction) Construct the first curvilinear unit vector
Ufor the given direction.The special case of the direction vector pointing along the z-axis is handled by forcing the unit vector to along the x-axis.
- Parameters
direction – is the input direction vector
- Returns
a normalized vector in the x-y plane orthogonal to the direction.
-
template<typename InputVector>
inline auto makeCurvilinearUnitVectors(const Eigen::MatrixBase<InputVector> &direction) Construct the curvilinear unit vectors
UandVfor the given direction.With
Tthe normalized input direction, the three vectorsU,V, andTform an orthonormal basis set, i.e. they satisfywith the additional condition thatU x V = T V x T = U T x U = V
Uis located in the global x-y plane.- Parameters
direction – is the input direction vector
- Returns
normalized unit vectors
UandVorthogonal to the direction.
-
template<typename T>
inline Eigen::Matrix<T, 3, 1> makeDirectionFromPhiEta(T phi, T eta) Construct a normalized direction vector from phi angle and pseudorapidity.
Note
The input arguments intentionally use the same template type so that a compile error occurs if inconsistent input types are used. Avoids unexpected implicit type conversions and forces the user to explicitly cast mismatched input types.
- Parameters
phi – is the direction angle in the x-y plane.
eta – is the pseudorapidity towards the z-axis.
-
template<typename T>
inline Eigen::Matrix<T, 3, 1> makeDirectionFromPhiTheta(T phi, T theta) Construct a normalized direction vector from phi and theta angle.
Note
The input arguments intentionally use the same template type so that a compile error occurs if inconsistent input types are used. Avoids unexpected implicit type conversions and forces the user to explicitly cast mismatched input types.
- Parameters
phi – is the direction angle in radian in the x-y plane.
theta – is the polar angle in radian towards the z-axis.
-
template<typename parameters_t, typename covariance_t, typename indices_t, typename ...tail_indices_t>
auto makeMeasurement(SourceLink source, const Eigen::MatrixBase<parameters_t> ¶ms, const Eigen::MatrixBase<covariance_t> &cov, indices_t index0, tail_indices_t... tailIndices) -> Measurement<indices_t, 1u + sizeof...(tail_indices_t)> Construct a fixed-size measurement for the given indices.
This helper function can be used to create a fixed-size measurement using an explicit set of indices, e.g.
for a 2d measurement w/ one position and time.auto m = makeMeasurement(s, p, c, eBoundLoc0, eBoundTime);
Note
The indices must be ordered and must be consistent with the content of parameters and covariance.
- Template Parameters
parameters_t – Input parameters vector type
covariance_t – Input covariance matrix type
indices_t – Parameter index type, determines the full parameter space
tail_indices_t – Helper types required to support variadic arguments; all types must be convertibale to
indices_t.
- Parameters
source – The link that connects to the underlying detector readout
params – Measured parameters values
cov – Measured parameters covariance
index0 – Required parameter index, measurement must be at least 1d
tailIndices – Additional parameter indices for larger measurements
- Returns
Fixed-size measurement w/ the correct type and given inputs
-
template<typename T>
inline Eigen::Matrix<T, 2, 1> makePhiThetaFromDirection(Eigen::Matrix<T, 3, 1> unitDir) Construct a phi and theta angle from a direction vector.
- Parameters
unitDir – 3D vector indicating a direction
-
MaterialGrid2D mapMaterialPoints(Grid2D &grid)
Average the material collected in a 2D grid and use it to create a 2D material grid.
- Parameters
grid – [in] The material collecting grid coordinate
- Returns
The average material grid decomposed into classification numbers
-
MaterialGrid3D mapMaterialPoints(Grid3D &grid)
Average the material collected in a 3D grid and use it to create a 3D material grid.
- Parameters
grid – [in] The material collecting grid coordinate
- Returns
The average material grid decomposed into classification numbers
-
MaterialMapper<detail::Grid<Material::ParametersVector, detail::EquidistantAxis, detail::EquidistantAxis>> materialMapperRZ(const std::function<size_t(std::array<size_t, 2> binsRZ, std::array<size_t, 2> nBinsRZ)> &materialVectorToGridMapper, std::vector<double> rPos, std::vector<double> zPos, const std::vector<Acts::Material> &material, double lengthUnit = UnitConstants::mm)
Method to setup the MaterialMapper.
e.g.: we have small grid with the values: r={2,3}, z ={4,5}, the corresponding indices are i (belonging to r) and j (belonging to z), the globalIndex is M (belonging to the values of the Material) and the map is:
r
i
z
j
M
2
0
4
0
0
2
0
5
1
1
3
1
4
0
2
3
1
5
1
3
In this case the function would look like:
[](std::array<size_t, 2> binsRZ, std::array<size_t, 2> nBinsRZ) { return (binsRZ.at(0) * nBinsRZ.at(1) + binsRZ.at(1)); }
Note
The values do not need to be sorted or unique (this will be done inside the function)
Note
The values do not need to be sorted or unique (this will be done inside the function)
Note
The function localToGlobalBin determines how the material was stored in the vector in respect to the grid values
- Parameters
materialVectorToGridMapper – [in] Function mapping the vector of material to the map of material values
rPos – [in] Values of the grid points in r
zPos – [in] Values of the grid points in z
material – [in] The material classification values in r and z for all given grid points stored in a vector
lengthUnit – [in] The unit of the grid points
-
MaterialMapper<detail::Grid<Material::ParametersVector, detail::EquidistantAxis, detail::EquidistantAxis, detail::EquidistantAxis>> materialMapperXYZ(const std::function<size_t(std::array<size_t, 3> binsXYZ, std::array<size_t, 3> nBinsXYZ)> &materialVectorToGridMapper, std::vector<double> xPos, std::vector<double> yPos, std::vector<double> zPos, const std::vector<Material> &material, double lengthUnit = UnitConstants::mm)
Method to setup the MaterialMapper.
e.g.: we have small grid with the values: x={2,3}, y={3,4}, z ={4,5}, the corresponding indices are i (belonging to x), j (belonging to y) and k (belonging to z), the globalIndex is M (belonging to the values of the Material) and the map is:
x
i
y
j
z
k
M
2
0
3
0
4
0
0
2
0
3
0
5
1
1
2
0
4
1
4
0
2
2
0
4
1
5
1
3
3
1
3
0
4
0
4
3
1
3
0
5
1
5
3
1
4
1
4
0
6
3
1
4
1
5
1
7
In this case the function would look like:
[](std::array<size_t, 3> binsXYZ, std::array<size_t, 3> nBinsXYZ) { return (binsXYZ.at(0) * (nBinsXYZ.at(1) * nBinsXYZ.at(2)) + binsXYZ.at(1) * nBinsXYZ.at(2) + binsXYZ.at(2)); }
Note
The values do not need to be sorted or unique (this will be done inside the function)
Note
The values do not need to be sorted or unique (this will be done inside the function)
Note
The values do not need to be sorted or unique (this will be done inside the function)
Note
The function localToGlobalBin determines how the material was stored in the vector in respect to the grid values
- Parameters
materialVectorToGridMapper – [in] Function mapping the vector of material to the map of material values
xPos – [in] Values of the grid points in x
yPos – [in] Values of the grid points in y
zPos – [in] Values of the grid points in z
material – [in] The material classification values in x, y and z for all given grid points stored in a vector
lengthUnit – [in] The unit of the grid points
-
template<typename Derived>
auto matrixToBitset(const Eigen::PlainObjectBase<Derived> &m) Convert an integer matrix to a bitset.
Note
How the bits are ordered depends on the storage type of the matrix being converted (row-major or col-major)
- Template Parameters
Derived – Eigen base concrete type
- Parameters
m – Matrix that is converted
- Returns
The converted bitset.
-
template<typename T>
std::array<typename T::value_type, 2u> min_max(const T &tseries) Return min/max from a (optionally) sorted series, obsolete with C++20 (ranges)
- Template Parameters
T – a numeric series
- Parameters
tseries – is the number series
- Returns
[ min, max ] in an array of length 2
-
inline bool operator!=(const DigitizationSourceLink &lhs, const DigitizationSourceLink &rhs)
-
inline bool operator!=(const SurfaceBounds &lhs, const SurfaceBounds &rhs)
-
inline constexpr double operator*(Direction dir, double value)
-
inline constexpr float operator*(Direction dir, float value)
-
inline constexpr int operator*(Direction dir, int value)
-
inline constexpr double operator*(double value, Direction dir)
-
inline constexpr float operator*(float value, Direction dir)
-
inline constexpr int operator*(int value, Direction dir)
-
inline constexpr double operator*=(double &value, Direction dir)
-
inline constexpr float operator*=(float &value, Direction dir)
-
inline constexpr int operator*=(int &value, Direction dir)
-
inline std::ostream &operator<<(std::ostream &os, BoundarySurfaceFace &face)
-
template<typename T, typename U, size_t V>
std::ostream &operator<<(std::ostream &os, const AxisAlignedBoundingBox<T, U, V> &box) Overload of the << operator for bounding boxes.
- Template Parameters
T – entity type
U – value type
V – dimension
- Parameters
os – The output stream
box – The bounding box
- Returns
The given output stream.
-
inline std::ostream &operator<<(std::ostream &os, const ConstrainedStep &step)
-
inline std::ostream &operator<<(std::ostream &os, const IVisualization3D &hlp)
Overload of the << operator to facilitate writing to streams.
- Parameters
os – The output stream
hlp – The helper instance
-
std::ostream &operator<<(std::ostream &os, const Material &material)
-
std::ostream &operator<<(std::ostream &os, const MaterialSlab &materialSlab)
-
template<typename T, size_t D>
std::ostream &operator<<(std::ostream &os, const Ray<T, D> &ray) Overload of the outstream operator.
- Parameters
os – The out stream
ray – The ray to write to
os
- Returns
The outstream given in
os
-
inline std::ostream &operator<<(std::ostream &os, const std::tuple<const Surface&, const GeometryContext&> &tup)
Print surface information to the provided stream.
Internally invokes the
surface.toStream(...)-method. This can be easily used e.g. likestd::cout << std::tie(surface, geometryContext);
-
inline std::ostream &operator<<(std::ostream &os, const SurfaceBounds &sb)
-
template<typename indices_t>
std::ostream &operator<<(std::ostream &os, const VariantMeasurement<indices_t> &vm)
-
std::ostream &operator<<(std::ostream &os, Direction dir)
-
std::ostream &operator<<(std::ostream &os, GeometryIdentifier id)
-
inline std::ostream &operator<<(std::ostream &os, IntersectionStatus status)
Ostream-operator for the IntersectionStatus enum.
-
std::ostream &operator<<(std::ostream &os, MaterialUpdateStage matUpdate)
-
std::ostream &operator<<(std::ostream &os, PdgParticle pdg)
Print PDG particle numbers with a descriptive name.
-
std::ostream &operator<<(std::ostream &os, TrackStatePropMask mask)
-
std::ostream &operator<<(std::ostream &sl, const BinUtility &bgen)
Overload of << operator for std::ostream for debug output.
-
std::ostream &operator<<(std::ostream &sl, const Extent &rhs)
Overload of << operator for std::ostream for debug output.
-
std::ostream &operator<<(std::ostream &sl, const GlueVolumesDescriptor &gvd)
-
std::ostream &operator<<(std::ostream &sl, const Volume &vol)
Overload of << operator for std::ostream for debug output.
-
std::ostream &operator<<(std::ostream &sl, const VolumeBounds &vb)
Overload of << operator for std::ostream for debug output.
-
inline bool operator==(const DigitizationSourceLink &lhs, const DigitizationSourceLink &rhs)
-
inline bool operator==(const SurfaceBounds &lhs, const SurfaceBounds &rhs)
-
inline bool operator==(const VolumeBounds &lhs, const VolumeBounds &rhs)
-
std::optional<std::string_view> pdgToShortAbsString(PdgParticle pdg)
-
template<typename T>
std::tuple<typename T::value_type, ActsScalar> range_medium(const T &tseries) Return range and medium of a sorted numeric series.
- Template Parameters
T – a numeric series
- Parameters
tseries – is the number series
- Returns
[ range, medium ] in an tuple
-
template<typename mixture_t, typename projector_t = Acts::Identity>
auto reduceGaussianMixture(const mixture_t &mixture, const Surface &surface, MixtureReductionMethod method, projector_t &&projector = projector_t{}) Reduce Gaussian mixture.
- Parameters
mixture – The mixture iterable
surface – The surface, on which the bound state is
method – How to reduce the mixture
projector – How to project a element of the iterable to something like a std::tuple< double, BoundVector, BoundMatrix >
- Returns
parameters and covariance as std::tuple< BoundVector, BoundMatrix >
-
template<typename T>
T safeExp(T val) noexcept Calculate the exponential function while avoiding FPEs.
Note
The boundary values of -50.0 and 50.0 might need to be adapted when using this function with doubles
- Parameters
val – argument for which the exponential function should be evaluated.
- Returns
0 in the case of underflow, std::numeric_limits<T>::infinity in the case of overflow, std::exp(val) else
-
template<typename MatrixType, typename ResultType = MatrixType>
std::optional<ResultType> safeInverse(const MatrixType &m) noexcept FPE “safe” functions.
Our main motivation for this is that users might have a strict FPE policy which would flag every single occurrence as a failure and then sombody has to investigate. Since we are processing a high number of events and floating point numbers sometimes work in mysterious ways the caller of this function might want to hide FPEs and handle them in a more controlled way. Calculate the inverse of an Eigen matrix after checking if it can be numerically inverted. This allows to catch potential FPEs before they occur.
- Template Parameters
Derived – Eigen derived concrete type
Result – Eigen result type defaulted to input type
- Parameters
m – Eigen matrix to invert
- Returns
The theta value
-
Acts::InterpolatedBFieldMap<Acts::detail::Grid<Acts::Vector2, Acts::detail::EquidistantAxis, Acts::detail::EquidistantAxis>> solenoidFieldMap(std::pair<double, double> rlim, std::pair<double, double> zlim, std::pair<size_t, size_t> nbins, const SolenoidBField &field)
Function which takes an existing SolenoidBField instance and creates a field mapper by sampling grid points from the analytical solenoid field.
- Parameters
rlim – pair of r bounds
zlim – pair of z bounds
nbins – pair of bin counts
field – the solenoid field instance
- Returns
A field map instance for use in interpolation.
-
inline void sortDetElementsByID(std::vector<dd4hep::DetElement> &det)
Sort function which sorts dd4hep::DetElement by their ID.
- Parameters
det – [inout] the dd4hep::DetElements to be sorted
-
std::shared_ptr<Surface> surfaceFromJson(const nlohmann::json &j)
Conversion to Surface from jsonn.
- Parameters
j – the read-in json object
- Returns
a shared_ptr to a surface object for type polymorphism
Conversion to Surface from json in correct type.
The type is given as a template argument in order to be able to construct the correct fitting types for surfaces.
- Parameters
j – the read-in json object
- Returns
a shared_ptr to a typed surface object for type polymorphism
-
template<template<size_t> class Callable, size_t N, size_t NMAX, typename ...Args>
auto template_switch(size_t v, Args&&... args) Dispatch a call based on a runtime value on a function taking the value at compile time.
This function allows to write a templated functor, which accepts a
size_tlike parameter at compile time. It is then possible to make a call to the corresponding instance of the functor based on a runtime value. To achieve this, the function essentially created a if cascade betweenNandNMAX, attempting to find the right instance. Because the cascade is visible to the compiler entirely, it should be able to optimize.Note
Callableis expected to have a static member functioninvokethat is callable withArgs- Template Parameters
Callable – Type which takes a size_t as a compile time param
N – Value from which to start the dispatch chain, i.e. 0 in most cases
NMAX – Maximum value up to which to attempt a dispatch
- Parameters
v – The runtime value to dispatch on
args – Additional arguments passed to
Callable::invoke().
-
template<size_t N, size_t NMAX, typename Lambda, typename ...Args>
auto template_switch_lambda(size_t v, Lambda &&func, Args&&... args) Alternative version of
template_switchwhich accepts a generic lambda and communicates the dimension via an integral constant type.- Template Parameters
N – Value from which to start the dispatch chain, i.e. 0 in most cases
NMAX – Maximum value up to which to attempt a dispatch
- Parameters
v – The runtime value to dispatch on
func – The lambda to invoke
args – Additional arguments passed to
func
-
template<std::size_t kDIM, typename value_type>
std::array<value_type, kDIM> to_array(const std::vector<value_type> &vecvals) This can be abandoned with C++20 to use the std::to_array method.
Note
only the first kDIM elements will obviously be filled, if the vector tends to be longer, it is truncated
- Parameters
vecvals – the vector of bound values to be converted
- Returns
an array with the filled values
-
void to_json(nlohmann::json &j, const BinningData &bd)
-
void to_json(nlohmann::json &j, const BinUtility &bu)
-
void to_json(nlohmann::json &j, const Extent &e)
-
void to_json(nlohmann::json &j, const Material &t)
-
void to_json(nlohmann::json &j, const MaterialSlab &t)
-
void to_json(nlohmann::json &j, const ProtoDetector &pd)
-
void to_json(nlohmann::json &j, const ProtoVolume &pv)
Non-contextual conversion of a surface.
Note
it will take the default context
-
void to_json(nlohmann::json &j, const Surface &surface)
Non-contextual conversion of a surface.
Note
it will take the default context
-
void to_json(nlohmann::json &j, const SurfaceAndMaterialWithContext &surface)
Conversion of a pair of surface and material used for the material mapping.
-
void to_json(nlohmann::json &j, const SurfaceBounds &bounds)
-
void to_json(nlohmann::json &j, const surfaceMaterialPointer &material)
-
void to_json(nlohmann::json &j, const TrackingVolumeAndMaterial &volume)
Conversion of a pair of tracking volume and material used for the material mapping.
-
void to_json(nlohmann::json &j, const TrackingVolumePointer &volume)
Conversion of a const pointer on a tracking volume used to write the geometry.
Conversion of a tracking volume.
-
void to_json(nlohmann::json &j, const Transform3 &t)
-
void to_json(nlohmann::json &j, const VolumeBounds &bounds)
-
void to_json(nlohmann::json &j, const volumeMaterialPointer &material)
Contextual conversion of a surface.
- Parameters
j – the json to be filled
surface – the surface to be converted
gctx – the geometry context for this
-
inline std::string toString(const Acts::Transform3 &transform, int precision = 4, const std::string &offset = "")
Print out a transform in a structured way.
- Parameters
transform – The transform to print
precision – Numeric output precision
offset – Offset in front of matrix lines
- Returns
The printed string
-
inline std::string toString(const Acts::Translation3 &translation, int precision = 4)
Print out a translation in a structured way.
- Parameters
translation – The translation to print
precision – Numeric output precision
- Returns
The printed string
-
template<typename derived_t>
inline std::string toString(const Eigen::MatrixBase<derived_t> &matrix, int precision = 4, const std::string &offset = "") Print out a matrix in a structured way.
- Template Parameters
derived_t – Type of the matrix
- Parameters
matrix – The matrix to print
precision – Numeric output precision
offset – Offset in front of matrix lines
- Returns
The printed string
-
template<ACTS_CONCEPT track_container_t(TrackContainerBackend), typename traj_t>
TrackContainer(const track_container_t &container, const traj_t &traj) -> TrackContainer<track_container_t, traj_t, detail::ConstRefHolder>
-
template<ACTS_CONCEPT track_container_t(TrackContainerBackend), typename traj_t>
TrackContainer(track_container_t &&container, traj_t &&traj) -> TrackContainer<track_container_t, traj_t, detail::ValueHolder>
-
template<ACTS_CONCEPT track_container_t(TrackContainerBackend), typename traj_t>
TrackContainer(track_container_t &container, traj_t &traj) -> TrackContainer<track_container_t, traj_t, detail::RefHolder>
-
template<typename external_spacepoint_t, typename callable_t>
void transformCoordinates(Acts::SpacePointData &spacePointData, const std::vector<external_spacepoint_t*> &vec, const external_spacepoint_t &spM, bool bottom, std::vector<LinCircle> &linCircleVec, callable_t &&extractFunction)
-
template<typename external_spacepoint_t>
void transformCoordinates(Acts::SpacePointData &spacePointData, const std::vector<InternalSpacePoint<external_spacepoint_t>*> &vec, const InternalSpacePoint<external_spacepoint_t> &spM, bool bottom, std::vector<LinCircle> &linCircleVec) Transform a vector of spacepoints to u-v space circles with respect to a given middle spacepoint.
- Template Parameters
external_spacepoint_t – The external spacepoint type.
- Parameters
spacePointData – [in] Auxiliary variables used by the seeding
vec – [in] The list of bottom or top spacepoints
spM – [in] The middle spacepoint.
bottom – [in] Should be true if vec are bottom spacepoints.
linCircleVec – [out] The output vector to write to.
-
template<typename external_spacepoint_t, typename callable_t>
LinCircle transformCoordinates(const external_spacepoint_t &sp, const external_spacepoint_t &spM, bool bottom, callable_t &&extractFunction)
-
template<typename external_spacepoint_t>
LinCircle transformCoordinates(const InternalSpacePoint<external_spacepoint_t> &sp, const InternalSpacePoint<external_spacepoint_t> &spM, bool bottom) Transform two spacepoints to a u-v space circle.
This function is a non-vectorized version of transformCoordinates.
- Template Parameters
external_spacepoint_t – The external spacepoint type.
- Parameters
sp – [in] The first spacepoint to use, either a bottom or top.
spM – [in] The middle spacepoint to use.
bottom – [in] Should be true if sp is a bottom SP.
-
std::tuple<VariantCovariance, VariantTransportJacobian> transportCovarianceToBound(const GeometryContext &gctx, const Surface &surface, const FreeVector ¶meters, CovarianceCache &cCache)
Transport the covariance to a new (surface) bound definition.
- Parameters
gctx – [in] The current geometry context
surface – [in] The surface of the bound representation
parameters – [in] The free parametrisation on the surface
cCache – [in,out] the covariance cache (to be modified)
- Returns
a variant transport jacobian
-
std::tuple<VariantCovariance, VariantTransportJacobian> transportCovarianceToCurvilinear(const Vector3 &direction, CovarianceCache &cCache)
Transport the covariance to a new (curvilinear) bound definition.
- Parameters
direction – [in] The track direction at the new curvilinear definition
cCache – [in,out] the covariance cache (to be modified)
-
std::tuple<VariantCovariance, VariantTransportJacobian> transportCovarianceToFree(CovarianceCache &cCache)
Transport the covariance to a new free definition.
- Parameters
cCache – [in,out] the covariance cache (to be modified)
Helper function to unpack a vector of
shared_ptrinto a vector of raw pointers.- Template Parameters
T – the stored type
- Parameters
items – The vector of
shared_ptr- Returns
The unpacked vector
Helper function to unpack a vector of
shared_ptrinto a vector of raw pointers (const version)- Template Parameters
T – the stored type
- Parameters
items – The vector of
shared_ptr- Returns
The unpacked vector
Helper function to unpack a vector of
shared_ptrinto a vector of raw pointers.- Template Parameters
T – the stored type
- Parameters
items – The vector of
shared_ptr- Returns
The unpacked vector
-
template<typename L, typename A, typename B>
auto visit_measurement(A &¶m, B &&cov, size_t dim, L &&lambda) Dispatch a lambda call on an overallocated parameter vector and covariance matrix, based on a runtime dimension value.
Inside the lambda call, the vector and matrix will have fixed dimensions, but will still point back to the originally given overallocated values.
Note
No requirements on
AandBare made, to enable a single overload for both const and non-const matrices/vectors.- Template Parameters
L – The lambda type
A – The parameter vector type
B – The covariance matrix type
- Parameters
param – The parameter vector
cov – The covariance matrix
dim – The actual dimension as a runtime value
lambda – The lambda to call with the statically sized subsets
-
template<typename L>
auto visit_measurement(size_t dim, L &&lambda) Dispatch a generic lambda on a measurement dimension.
This overload doesn’t assume anything about what is needed inside the lambda, it communicates the dimension via an integral constant type
- Template Parameters
L – The generic lambda type to call
- Parameters
dim – The runtime dimension of the measurement
lambda – The generic lambda instance to call
- Returns
Returns the lambda return value
-
std::shared_ptr<const CylinderVolumeBuilder> volumeBuilder_dd4hep(dd4hep::DetElement subDetector, const Logger &logger, BinningType bTypePhi = equidistant, BinningType bTypeR = equidistant, BinningType bTypeZ = equidistant, double layerEnvelopeR = UnitConstants::mm, double layerEnvelopeZ = UnitConstants::mm, double defaultLayerThickness = UnitConstants::fm)
Method internally used to create an Acts::CylinderVolumeBuilder.
This method creates an Acts::CylinderVolumeBuilder from a sub detector (= ‘compound’ DetElement or DetElements which are declared as ‘isBarrel’ or ‘isBeampipe’ by their extension.
- Attention
The default thickness should be set thin enough that no touching or overlapping with the next layer can happen.
Note
Possible binningtypes:
arbitrary - of the sizes if the surfaces and the distance in between vary. This mode finds out the bin boundaries by scanning through the surfaces.
equidistant - if the sensitive surfaces are placed equidistantly
Note
equidistant binningtype is recommended because it is faster not only while building the geometry but also for look up during the extrapolation
Note
Layers containing surfaces per default are not allowed to be attached to each other (navigation will fail at this point). However, to allow material layers (not containing surfaces) to be attached to each other, this default thickness is needed. In this way, the layer will be thin (with space to the next layer), but the material will have the’real’ thickness.
- Parameters
subDetector – [in] the DD4hep DetElement of the subdetector
logger – [in] A logger instance
bTypePhi – [in] is how the sensitive surfaces (modules) should be binned in a layer in phi direction.
bTypeR – [in] is how the sensitive surfaces (modules) should be binned in a layer in r direction
bTypeZ – [in] is how the sensitive surfaces (modules) should be binned in a layer in z direction
layerEnvelopeR – [in] the tolerance added to the geometrical extension in r of the layers contained to build the volume envelope around
layerEnvelopeZ – [in] the tolerance added to the geometrical extension in z of the layers contained to build the volume envelope around
defaultLayerThickness – [in] In case no surfaces (to be contained by the layer) are handed over, the layer thickness will be set to this value
- Returns
std::shared_ptr the Acts::CylinderVolumeBuilder which can be used to build the full tracking geometry
-
template<typename external_spacepoint_t>
bool xyzCoordinateCheck(Acts::SpacePointData &spacePointData, const Acts::SeedFinderConfig<external_spacepoint_t> &config, const Acts::InternalSpacePoint<external_spacepoint_t> &sp, const double *spacepointPosition, double *outputCoordinates) Check the compatibility of spacepoint coordinates in xyz assuming the Bottom-Middle direction with the strip meassument details.
- Template Parameters
external_spacepoint_t – The external spacepoint type.
- Parameters
spacePointData – [in] Auxiliary variables used by the seeding
config – [in] SeedFinder config containing the delegates to the strip measurement details.
sp – [in] Input space point used in the check.
spacepointPosition – [in] Spacepoint coordinates in xyz plane.
outputCoordinates – [out] The output vector to write to.
- Returns
Boolean that says if spacepoint is compatible with being inside the detector element.
-
template<typename ...R>
auto zip(R&&... r) Function that allows to zip some ranges to be used in a range-based for loop.
When wanting to mutate the entries, the result must be captured by value:
for(auto [a, b, c] : zip(ra, rb, rc)) { a+=2; }
Note
the behaviour is undefined if the ranges do not have equal range
- Template Parameters
R – The ranges type pack
- Parameters
r – The ranges parameter pack
Variables
-
static constexpr TrackIndexType kTrackIndexInvalid = std::numeric_limits<TrackIndexType>::max()
-
template<typename fitter>
constexpr bool LinearizerConcept = Acts::Concepts::Linearizer::LinearizerConcept<fitter>::value
-
constexpr int PolygonDynamic = -1
Tag to trigger specialization of a dynamic polygon.
-
static const std::vector<BinningValue> s_binningValues = {binX, binY, binZ, binR, binPhi, binRPhi, binH, binEta, binMag}
static list of all binning values
-
static constexpr ActsScalar s_curvilinearProjTolerance = 0.999995
Tolerance for not being within curvilinear projection this allows using the same curvilinear frame to eta = 6, validity tested with IntegrationTests/PropagationTest.
-
static constexpr ActsScalar s_epsilon = 3 * std::numeric_limits<ActsScalar>::epsilon()
Tolerance for being numerical equal for geometry building.
-
static const InfiniteBounds s_noBounds = {}
-
static constexpr ActsScalar s_onSurfaceTolerance = 1e-4
Tolerance for being on Surface.
Note
This is intentionally given w/o an explicit unit to avoid having to include the units header unnecessarily. With the native length unit of mm this corresponds to 0.1um.
-
static const Transform3 s_planeXY = Transform3::Identity()
-
static const Transform3 s_planeYZ = AngleAxis3(0.5 * M_PI, Vector3::UnitY()) * AngleAxis3(0.5 * M_PI, Vector3::UnitZ()) * Transform3::Identity()
-
static const Transform3 s_planeZX = AngleAxis3(-0.5 * M_PI, Vector3::UnitX()) * AngleAxis3(-0.5 * M_PI, Vector3::UnitZ()) * Transform3::Identity()
-
static ViewConfig s_viewFiltered = ViewConfig({255, 255, 0})
-
static ViewConfig s_viewGrid = ViewConfig({220, 0, 0})
-
static ViewConfig s_viewLine = ViewConfig({0, 0, 220})
-
static ViewConfig s_viewMeasurement = ViewConfig({255, 102, 0})
-
static ViewConfig s_viewParameter = ViewConfig({0, 0, 255})
-
static ViewConfig s_viewPassive = ViewConfig({240, 280, 0})
-
static ViewConfig s_viewPredicted = ViewConfig({51, 204, 51})
-
static ViewConfig s_viewSensitive = ViewConfig({0, 180, 240})
-
static ViewConfig s_viewSmoothed = ViewConfig({0, 102, 255})
-
static ViewConfig s_viewVolume = ViewConfig({220, 220, 0})
-
template<typename accessor>
constexpr bool SourceLinkAccessorConcept = Acts::Concepts::SourceLinkAccessor::SourceLinkAccessorConcept<accessor>::value
-
template<typename stepper, typename state = typename stepper::State>
constexpr bool StepperConcept = Acts::Concepts::Stepper::SingleStepperConcept<stepper, state>::value || Acts::Concepts::Stepper::MultiStepperConcept<stepper, state>::value
-
template<typename stepper>
constexpr bool StepperStateConcept = Acts::Concepts::Stepper::StepperStateConcept<stepper> || Acts::Concepts::Stepper::MultiStepperStateConcept<stepper>
-
template<typename finder>
constexpr bool VertexFinderConcept = Acts::Concepts::VertexFinder::VertexFinderConcept<finder>::value
-
template<typename fitter>
constexpr bool VertexFitterConcept = Acts::Concepts::VertexFitter::VertexFitterConcept<fitter>::value
-
constexpr Envelope zeroEnvelope = {0, 0}
-
constexpr ExtentEnvelope zeroEnvelopes = {zeroEnvelope, zeroEnvelope, zeroEnvelope, zeroEnvelope, zeroEnvelope, zeroEnvelope, zeroEnvelope, zeroEnvelope}
-
class AbstractVolume : public Acts::Volume
- #include <Acts/Geometry/AbstractVolume.hpp>
AbstractVolume description inside the tracking realm.
This is the purely geometrical object volume.
The Acts::AbstractVolume is constructed by giving a pointer to a Transform3 and a pointer to Acts::VolumeBounds, this implies that the ownership of the objects pointed to is passed as well. For memory optimisation, the AbstractVolume can also be constructed with shared_ptr objects.
A Acts::AbstractVolume is at first a collection class of Acts::BoundarySurface, the vector of Acts::BoundarySurface is returned by the Acts::VolumeBounds that carry a decompose method.
Boundary surfaces can be shared between AbstractVolumes to enhance automatic navigation between AbstractVolumes, therefore they are reference counted by a std::shared_ptr holder class.
Public Functions
-
AbstractVolume() = delete
-
AbstractVolume(const AbstractVolume &vol) = default
-
AbstractVolume(const Transform3 &transform, VolumeBoundsPtr volbounds)
Constructor with shared Transform3*, VolumeBounds*.
- Parameters
transform – is the global 3d transformation into the volume frame
volbounds – is the boundary definition
-
~AbstractVolume() override = default
-
const std::vector<BoundarySurfacePtr> &boundarySurfaces() const
Method to return the BoundarySurfaces.
- Returns
the vector of boundary surfaces
-
AbstractVolume &operator=(const AbstractVolume &vol) = delete
-
AbstractVolume() = delete
-
class AccumulatedMaterialSlab
- #include <Acts/Material/AccumulatedMaterialSlab.hpp>
Accumulate material properties from multiple hits/track and multiple tracks.
This is a helper class for the
SurfaceMaterialMapperto handle material accumulation and averaging for one surface bin. The accumulation procedure is done in two steps:The per-track store accumulates material steps from one track/particle. Multiple material steps can be assigned to the same bin time by one particle, e.g. if the simulation has created more than one step in the material or if several components are compressed into one description. Multiple steps are treated as if they are passed one after the other.
The total store averages the accumulated material properties over all tracks. Each track contributes equally.
Public Functions
-
void accumulate(MaterialSlab slabAlongTrack, float pathCorrection = 1)
Add the material to the current per-track store.
The recoded material slab is assumed to be defined along the track direction. The track can have non-perpendicular incidence on the surface and the recorded slab has to be projected along the surface normal. The path correction gives the scaling factor from normal incidence to the recorded incidence as provided by the
Surfaceinterface.Vacuum steps with a non-zero thickness can be added to account for holes in material structures.
- Parameters
slabAlongTrack – Recorded equivalent material slab for this step
pathCorrection – Correction factor due to non-perpendicular incident
-
std::pair<MaterialSlab, unsigned int> totalAverage() const
Return the average material properties from all accumulated tracks.
Only contains the information up to the last
.trackAverage(...)call. If there have been additional calls to.accumulate(...)afterwards, the information is not part of the total average. The thickness corresponds to the average thickness seen by the tracks.- Returns
Average material properties and the number of contributing tracks
-
std::pair<float, unsigned int> totalVariance() const
Return the material variance from all accumulated tracks.
Only contains the information up to the last
.trackVariance(...)call. If there have been additional calls to.accumulate(...)afterwards, the information is not part of the total average. The number of tracks is only opdated on the call of.trackAverage(...)- Returns
Average material properties and the number of contributing tracks
-
void trackAverage(bool useEmptyTrack = false)
Add the accumulated material for the current track to the total average.
This finishes the material accumulation for the current track and resets the per-track store. Subsequent calls to
.accumulate(...)will start accumulating material for a new track.Each track contributes equally to the total average regardless of its measured path within the material. An empty per-track store, i.e. vanishing per-track material thickness, does not contribute to the total unless explicitly requested.
- Parameters
useEmptyTrack – indicate whether to consider an empty track store
-
void trackVariance(MaterialSlab slabReference, bool useEmptyTrack = false)
Use the accumulated material to update the material variance.
The material variance can be used to optimised the mapping process as it should be inversly proportionnal to the map quality
- Parameters
slabReference – reference slab (from the map) used to compute the variance
useEmptyTrack – indicate whether to consider an empty track store
-
class AccumulatedSurfaceMaterial
- #include <Acts/Material/AccumulatedSurfaceMaterial.hpp>
This class is used by the SurfaceMaterialMapper in order to accumulate/collect material information during the mapping process.
It performs event- and run-average when called, and returns a new SurfaceMaterial object as a unique_ptr after finalisation
Public Types
-
using AccumulatedMatrix = std::vector<AccumulatedVector>
-
using AccumulatedVector = std::vector<AccumulatedMaterialSlab>
Public Functions
-
AccumulatedSurfaceMaterial(AccumulatedSurfaceMaterial &&asma) = default
Copy Move Constructor.
- Parameters
asma – is the source object to be copied
-
AccumulatedSurfaceMaterial(const AccumulatedSurfaceMaterial &asma) = default
Copy Constructor.
- Parameters
asma – is the source object to be copied
-
AccumulatedSurfaceMaterial(const BinUtility &binUtility, double splitFactor = 0.)
Explicit constructor with only full MaterialSlab, for one-dimensional binning.
The split factors:
1. : oppositePre
0. : alongPre ===> 1 Dimensional array
- Parameters
binUtility – defines the binning structure on the surface
splitFactor – is the pre/post splitting directive
-
AccumulatedSurfaceMaterial(double splitFactor = 0.)
Default Constructor - for homogeneous material.
- Parameters
splitFactor – is the pre/post splitting directive
-
~AccumulatedSurfaceMaterial() = default
Destructor.
-
std::array<size_t, 3> accumulate(const Vector2 &lp, const MaterialSlab &mp, double pathCorrection = 1.)
Assign a material properties object.
- Parameters
lp – local position for the bin assignment
mp – material properties to be assigned
pathCorrection – Correction factor for the effective path length
- Returns
the bin triple to which the material was assigned
-
std::array<size_t, 3> accumulate(const Vector3 &gp, const MaterialSlab &mp, double pathCorrection = 1.)
Assign a material properties object.
- Parameters
gp – global position for the bin assignment
mp – material properties to be assigned
pathCorrection – Correction factor for the effective path length
- Returns
the bin triple to which the material was assigned
-
inline const AccumulatedMatrix &accumulatedMaterial() const
Access to the accumulated material.
-
inline const BinUtility &binUtility() const
Return the BinUtility.
-
AccumulatedSurfaceMaterial &operator=(AccumulatedSurfaceMaterial &&asma) = default
Assignment Move operator.
- Parameters
asma – is the source object to be copied
-
AccumulatedSurfaceMaterial &operator=(const AccumulatedSurfaceMaterial &asma) = default
Assignment operator.
- Parameters
asma – is the source object to be copied
-
inline double splitFactor() const
Access to the split factor.
-
std::unique_ptr<const ISurfaceMaterial> totalAverage()
Total average creates SurfaceMaterial.
-
void trackAverage(const std::vector<std::array<size_t, 3>> &trackBins = {}, bool emptyHit = false)
Average the information accumulated from one mapped track.
- Parameters
trackBins – The bins that were touched by this event
emptyHit – indicator if this is an empty assignment If none is given, the average runs over all bins in the surface map
-
void trackAverage(const Vector3 &gp, bool emptyHit = false)
Average the information accumulated from one mapped track.
- Parameters
gp – global position for the bin assignment
emptyHit – indicator if this is an empty assignment
-
void trackVariance(const std::vector<std::array<size_t, 3>> &trackBins, MaterialSlab slabReference, bool emptyHit = false)
Use the accumulated material to update the material variance.
- Parameters
trackBins – The bins that were touched by this event
emptyHit – indicator if this is an empty assignment
slabReference – reference slab (from the map) used to compute the variance If none is given, the average runs over all bins in the surface map
-
void trackVariance(const Vector3 &gp, MaterialSlab slabReference, bool emptyHit = false)
Use the accumulated material to update the material variance.
- Parameters
gp – global position for the bin assignment
emptyHit – indicator if this is an empty assignment
slabReference – indicator if this is an empty assignment
-
using AccumulatedMatrix = std::vector<AccumulatedVector>
-
class AccumulatedVolumeMaterial
- #include <Acts/Material/AccumulatedVolumeMaterial.hpp>
Accumulate and average volume-based material properties.
This class is intended to be used during the mapping process.
Public Functions
-
void accumulate(const MaterialSlab &mat)
Add one entry with the given material properties.
-
inline const Material &average()
Compute the average material collected so far.
- Returns
Vacuum properties if no matter has been accumulated yet.
-
void accumulate(const MaterialSlab &mat)
-
template<int trkGridSize = 15, typename vfitter_t = DummyVertexFitter<>>
class AdaptiveGridDensityVertexFinder - #include <Acts/Vertexing/AdaptiveGridDensityVertexFinder.hpp>
Vertex finder that makes use of a track density grid.
Each single track is modelled as a 2-dim Gaussian distribution grid in the d0-z0 plane, but only the overlap with the z-axis (i.e. a 1-dim density vector) needs to be calculated. All track contributions along the beam axis (main density vector) are superimposed and the z-value of the bin with the highest track density is returned as a vertex candidate. Unlike the GridDensityVertexFinder, this seeder implements an adaptive version where the density grid grows bigger with added tracks.
- Template Parameters
trkGridSize – The 2-dim grid size of a single track, i.e. a single track is modelled as a (trkGridSize x trkGridSize) grid in the d0-z0 plane. Note: trkGridSize has to be an odd value.
Public Types
-
using DensityMap = typename GridDensity::DensityMap
Public Functions
-
template<typename T = InputTrack_t, std::enable_if_t<std::is_same<T, BoundTrackParameters>::value, int> = 0>
inline AdaptiveGridDensityVertexFinder() Default constructor used if InputTrack_t type == BoundTrackParameters.
-
template<typename T = InputTrack_t, std::enable_if_t<std::is_same<T, BoundTrackParameters>::value, int> = 0>
inline AdaptiveGridDensityVertexFinder(const Config &cfg) Constructor used if InputTrack_t type == BoundTrackParameters.
- Parameters
cfg – Configuration object
-
inline AdaptiveGridDensityVertexFinder(const Config &cfg, const std::function<BoundTrackParameters(InputTrack_t)> &func)
Constructor for user-defined InputTrack_t type =! BoundTrackParameters.
- Parameters
cfg – Configuration object
func – Function extracting BoundTrackParameters from InputTrack_t object
-
inline AdaptiveGridDensityVertexFinder(const std::function<BoundTrackParameters(InputTrack_t)> &func)
Constructor for user-defined InputTrack_t type =! BoundTrackParameters with default Config object.
- Parameters
func – Function extracting BoundTrackParameters from InputTrack_t object
-
Result<std::vector<Vertex<InputTrack_t>>> find(const std::vector<const InputTrack_t*> &trackVector, const VertexingOptions<InputTrack_t> &vertexingOptions, State &state) const
Function that finds single vertex candidate.
- Parameters
trackVector – Input track collection
vertexingOptions – Vertexing options
state – The state object to cache the density grid and density contributions of each track, to be used if cacheGridStateForTrackRemoval == true
- Returns
Vector of vertices, filled with a single vertex (for consistent interfaces)
-
struct Config
- #include <Acts/Vertexing/AdaptiveGridDensityVertexFinder.hpp>
The Config struct.
Public Functions
-
inline Config(const GridDensity &gDensity)
- Parameters
gDensity – The grid density
-
inline Config(float binSize = 0.1)
- Parameters
binSize – Bin size of grid in mm
Public Members
-
bool cacheGridStateForTrackRemoval = true
-
double d0SignificanceCut = maxD0TrackSignificance * maxD0TrackSignificance
-
bool estimateSeedWidth = false
-
GridDensity gridDensity
-
double maxD0TrackSignificance = 3.5
-
double maxZ0TrackSignificance = 12.
-
double z0SignificanceCut = maxZ0TrackSignificance * maxZ0TrackSignificance
-
inline Config(const GridDensity &gDensity)
-
struct State
- #include <Acts/Vertexing/AdaptiveGridDensityVertexFinder.hpp>
The State struct.
Only needed if cacheGridStateForTrackRemoval == true
Public Members
-
bool isInitialized = false
-
DensityMap mainDensityMap
-
std::unordered_map<const InputTrack_t*, DensityMap> trackDensities
-
std::unordered_map<const InputTrack_t*, bool> trackSelectionMap
-
std::vector<const InputTrack_t*> tracksToRemove
-
bool isInitialized = false
-
template<int trkGridSize = 15>
class AdaptiveGridTrackDensity - #include <Acts/Vertexing/AdaptiveGridTrackDensity.hpp>
Implements a 1-dim density grid to be filled with track Gaussian distributions.
Each single track is modelled as a 2-dim Gaussian distribution grid in the d0-z0 plane, but only the overlap with the z-axis (i.e. a 1-dim density vector) needs to be calculated. The position of the highest track density (of either a single bin or the sum of a certain region) can be determined. Single tracks can be cached and removed from the overall density. Unlike the GaussianGridTrackDensity, the overall density vector grows adaptively with the tracks densities being added to the grid.
- Template Parameters
trkGridSize – The 2-dim grid size of a single track, i.e. a single track is modelled as a (trkGridSize x trkGridSize) grid in the d0-z0 plane. Note: trkGridSize has to be an odd value.
Public Types
-
using DensityMap = std::unordered_map<int, float>
Public Functions
-
inline AdaptiveGridTrackDensity(const Config &cfg)
-
DensityMap addTrack(const BoundTrackParameters &trk, DensityMap &mainDensityMap) const
Adds a single track to the overall grid density.
- Parameters
trk – The track to be added.
mainDensityMap – Map from z bins to corresponding track density.
- Returns
The density map of the track that was added
-
Result<float> getMaxZPosition(DensityMap &densityMap) const
Returns the z position of maximum (surrounding) track density.
- Parameters
densityMap – Map from z bins to corresponding track density
- Returns
The z position of maximum track density
-
Result<std::pair<float, float>> getMaxZPositionAndWidth(DensityMap &densityMap) const
Returns the z position of maximum track density and the estimated width.
- Parameters
densityMap – Map from z bins to corresponding track density
- Returns
The z position of maximum track density and width
-
DensityMap::const_iterator highestDensityEntry(const DensityMap &densityMap) const
Finds the maximum density of a DensityMap.
- Parameters
densityMap – Map between z bins and corresponding density value
- Returns
Iterator of the map entry with the highest density value
-
void subtractTrack(const DensityMap &trackDensityMap, DensityMap &mainDensityMap) const
Removes a track from the overall grid density.
- Parameters
trackDensityMap – Map from z bins to corresponding track density. The track density comes from a single track.
mainDensityMap – Map from z bins to corresponding track density. The track density comes an arbitrary number of tracks.
-
struct Config
- #include <Acts/Vertexing/AdaptiveGridTrackDensity.hpp>
The configuration struct.
Public Functions
-
inline Config(float binSize_ = 0.1)
- Parameters
binSize_ – The binSize in mm
Public Members
-
float binSize
-
float maxRelativeDensityDev = 0.01
-
bool useHighestSumZPosition = false
-
inline Config(float binSize_ = 0.1)
-
template<typename vfitter_t, typename sfinder_t>
class AdaptiveMultiVertexFinder - #include <Acts/Vertexing/AdaptiveMultiVertexFinder.hpp>
Implements an iterative vertex finder.
Brief description of the algorithm implemented: TODO
- Template Parameters
vfitter_t – Vertex fitter type
sfinder_t – Seed finder type
Public Functions
-
AdaptiveMultiVertexFinder(AdaptiveMultiVertexFinder&&) = default
-
inline AdaptiveMultiVertexFinder(Config &cfg, std::function<BoundTrackParameters(InputTrack_t)> func, std::unique_ptr<const Logger> logger = getDefaultLogger("AdaptiveMultiVertexFinder", Logging::INFO))
Constructor for user-defined InputTrack_t type != BoundTrackParameters.
- Parameters
cfg – Configuration object
func – Function extracting BoundTrackParameters from InputTrack_t object
logger – The logging instance
-
template<typename T = InputTrack_t, std::enable_if_t<std::is_same<T, BoundTrackParameters>::value, int> = 0>
inline AdaptiveMultiVertexFinder(Config &cfg, std::unique_ptr<const Logger> logger = getDefaultLogger("AdaptiveMultiVertexFinder", Logging::INFO)) Constructor used if InputTrack_t type == BoundTrackParameters.
- Parameters
cfg – Configuration object
logger – The logging instance
-
Result<std::vector<Vertex<InputTrack_t>>> find(const std::vector<const InputTrack_t*> &allTracks, const VertexingOptions<InputTrack_t> &vertexingOptions, State &state) const
Function that performs the adaptive multi-vertex finding.
- Parameters
allTracks – Input track collection
vertexingOptions – Vertexing options
state – State for fulfilling interfaces
- Returns
Vector of all reconstructed vertices
-
struct Config
- #include <Acts/Vertexing/AdaptiveMultiVertexFinder.hpp>
Configuration struct.
Public Functions
Config constructor.
- Parameters
fitter – The vertex fitter
sfinder – The seed finder
ipEst – ImpactPointEstimator
lin – Track linearizer
bIn – Input magnetic field
Public Members
-
bool addSingleTrackVertices = false
-
std::shared_ptr<const MagneticFieldProvider> bField
-
std::pair<double, double> defaultConstrFitQuality = {0., -3.}
-
bool do3dSplitting = false
-
bool doRealMultiVertex = true
-
ImpactPointEstimator<InputTrack_t, Propagator_t> ipEstimator
-
Linearizer_t linearizer
-
double looseConstrValue = 1e+8
-
double maximumVertexContamination = 0.5
-
int maxIterations = 100
-
double maxMergeVertexSignificance = 3.
-
double maxVertexChi2 = 18.42
-
double minWeight = 0.0001
-
sfinder_t seedFinder
-
double tracksMaxSignificance = 5.
-
double tracksMaxZinterval = 3. * Acts::UnitConstants::mm
-
bool useFastCompatibility = true
-
bool useSeedConstraint = true
-
bool useVertexCovForIPEstimation = false
-
vfitter_t vertexFitter
-
struct State
- #include <Acts/Vertexing/AdaptiveMultiVertexFinder.hpp>
State struct for fulfilling interface.
-
template<typename input_track_t, typename linearizer_t>
class AdaptiveMultiVertexFitter - #include <Acts/Vertexing/AdaptiveMultiVertexFitter.hpp>
Implements an adaptive multi-vertex fitter as described in detail in Section 5.3.5 in: Ref.
(1): CERN-THESIS-2010-027, Author: Piacquadio, Giacinto:
Identification of b-jets and investigation of the discovery potential of a Higgs boson in the WH−−>lvbb¯ channel with the ATLAS experiment- Template Parameters
input_track_t – Track object type
linearizer_t – Track linearizer type
Public Types
-
using InputTrack_t = input_track_t
-
using Linearizer_t = linearizer_t
-
using Propagator_t = typename linearizer_t::Propagator_t
Public Functions
-
inline AdaptiveMultiVertexFitter(Config &cfg, std::function<BoundTrackParameters(InputTrack_t)> func, std::unique_ptr<const Logger> logger = getDefaultLogger("AdaptiveMultiVertexFitter", Logging::INFO))
Constructor for user-defined InputTrack_t type != BoundTrackParameters.
- Parameters
cfg – Configuration object
func – Function extracting BoundTrackParameters from InputTrack_t object
logger – The logging instance
-
template<typename T = InputTrack_t, std::enable_if_t<std::is_same<T, BoundTrackParameters>::value, int> = 0>
inline AdaptiveMultiVertexFitter(Config &cfg, std::unique_ptr<const Logger> logger = getDefaultLogger("AdaptiveMultiVertexFitter", Logging::INFO)) Constructor used if InputTrack_t type == BoundTrackParameters.
- Parameters
cfg – Configuration object
logger – The logging instance
-
Result<void> addVtxToFit(State &state, Vertex<InputTrack_t> &newVertex, const Linearizer_t &linearizer, const VertexingOptions<InputTrack_t> &vertexingOptions) const
Adds new vertex to an existing multi-vertex fit and fits everything together (by invoking the fit_impl method):
The new vertex is added to the fit: all associated tracks get initialized, i.e. ParamsAtIP3d are created (from ImpactPointEstimator) to be later able to estimate in a fast way the compatibility of the tracks to their respective vertices.
All tracks belonging to the new vertex are scanned and all the vertices which share tracks with the new vertex to be fit are also added to the fit.
The multivertex fit is performed with all involved vertices.
This has the advantage that only vertices that are affected by adding the new vertex are refitted.
Note: newVertex has to be properly initialized (seed vertex, constraint vertex, list of MAV)
- Parameters
state – The state object
newVertex – New vertex to be added to fit
linearizer – The track linearizer
vertexingOptions – Vertexing options
- Returns
Result<void> object
-
Result<void> fit(State &state, const std::vector<Vertex<InputTrack_t>*> &verticesToFit, const Linearizer_t &linearizer, const VertexingOptions<InputTrack_t> &vertexingOptions) const
The actual fit function, performs a simultaneous fit of all vertices in
verticesToFitby invokingfitImpl- Parameters
state – The state object
verticesToFit – Vector containing all vertices to be fitted
linearizer – The track linearizer
vertexingOptions – Vertexing options
- Returns
Result<void> object
-
struct Config
- #include <Acts/Vertexing/AdaptiveMultiVertexFitter.hpp>
Public Functions
-
inline Config(const IPEstimator &est)
Config constructor.
- Parameters
est – ImpactPointEstimator
Public Members
-
AnnealingUtility annealingTool
Annealing tool used for a thermodynamic annealing scheme for the track weight factors in such a way that with high temperature values (at the beginning) only a slight preference is given to tracks compatible with the estimated vertex position.
With lower temperatures the weighting get stricter such that all incompatible tracks will be dropped at the end while keeping all compatible tracks with a weight=1. Ref. (1): CERN-THESIS-2010-027, Author: Piacquadio, Giacinto:
Identification of b-jets and investigation of the discovery potential of a Higgs boson in the WH−−>lvbb¯ channel with the ATLAS experiment
-
bool doSmoothing = {false}
-
IPEstimator ipEst
-
double maxDistToLinPoint = {0.5}
-
unsigned int maxIterations = {30}
-
double maxRelativeShift = {0.01}
-
double minWeight = {0.0001}
-
inline Config(const IPEstimator &est)
-
struct State
- #include <Acts/Vertexing/AdaptiveMultiVertexFitter.hpp>
The fitter state.
Public Functions
-
State() = default
Default State constructor.
-
inline State(const MagneticFieldProvider &field, const Acts::MagneticFieldContext &magContext)
-
inline void addVertexToMultiMap(Vertex<InputTrack_t> &vtx)
-
inline void removeVertexFromMultiMap(Vertex<InputTrack_t> &vtx)
Public Members
-
AnnealingUtility::State annealingState
-
IPEstimator::State ipState
-
Linearizer_t::State linearizerState
-
std::map<std::pair<const InputTrack_t*, Vertex<InputTrack_t>*>, TrackAtVertex<InputTrack_t>> tracksAtVerticesMap
-
std::multimap<const InputTrack_t*, Vertex<InputTrack_t>*> trackToVerticesMultiMap
-
std::vector<Vertex<InputTrack_t>*> vertexCollection
-
std::map<Vertex<InputTrack_t>*, VertexInfo<InputTrack_t>> vtxInfoMap
-
State() = default
-
class AmbiguityTrackClassifier
- #include </home/docs/checkouts/readthedocs.org/user_builds/acts/checkouts/v29.0.0/Plugins/Onnx/include/Acts/Plugins/Onnx/AmbiguityTrackClassifier.hpp>
Onnx model implementation for track scoring and selection.
Public Functions
-
inline AmbiguityTrackClassifier(const char *modelPath)
Construct the ambiguity scoring algorithm.
- Parameters
modelPath – path to the model file
-
template<typename track_container_t, typename traj_t, template<typename> class holder_t>
inline std::vector<std::vector<float>> inferScores(std::unordered_map<int, std::vector<int>> &clusters, const Acts::TrackContainer<track_container_t, traj_t, holder_t> &tracks) const Compute a score for each track to be used in the track selection.
- Parameters
clusters – is a map of clusters, each cluster correspond to a vector of track ID
tracks – is the input track container
- Returns
a vector of vector of track score. Due to the architecture of the network each track only have a size 1 score vector.
-
template<typename track_container_t, typename traj_t, template<typename> class holder_t>
inline std::vector<int> solveAmbuguity(std::unordered_map<int, std::vector<int>> &clusters, const Acts::TrackContainer<track_container_t, traj_t, holder_t> &tracks) const Select the track associated with each cluster.
- Parameters
clusters – is a map of clusters, each cluster correspond to a vector of track ID
tracks – is the input track container
- Returns
a vector of trackID corresponding tho the good tracks
-
inline std::vector<int> trackSelection(std::unordered_map<int, std::vector<int>> &clusters, std::vector<std::vector<float>> &outputTensor) const
Select the track associated with each cluster based on the score vector.
- Parameters
clusters – is a map of clusters, each cluster correspond to a vector of track ID
outputTensor – is the score vector obtained from inferScores.
- Returns
a vector of trackID corresponding tho the good tracks
-
inline AmbiguityTrackClassifier(const char *modelPath)
-
class AnnealingUtility
- #include <Acts/Utilities/AnnealingUtility.hpp>
Implements a deterministic thermodynamic annealing scheme Ref.
(1): CERN-THESIS-2010-027
Public Functions
-
void anneal(State &state) const
Does the actual annealing step.
-
double getWeight(State &state, double chi2) const
Weight access.
- Parameters
state – The state object
chi2 – Chi^2
- Returns
Calculated weight
-
double getWeight(State &state, double chi2, const std::vector<double> &allChi2) const
Weight access.
- Parameters
state – The state object
chi2 – Chi^2 for e.g. current track, i.e. compatibility of track to current vertex candidate
allChi2 – Vector of all chi^2 values, i.e. e.g. compatibilities of current track to all vertices it is currently attached to
- Returns
Calculated weight according to Eq.(5.46) in Ref.(1)
-
struct Config
- #include <Acts/Utilities/AnnealingUtility.hpp>
The configuration struct.
Public Functions
-
Config()
Public Members
-
double cutOff = {9.}
-
std::vector<double> setOfTemperatures = {64., 16., 4., 2., 1.5, 1.}
-
Config()
-
struct State
- #include <Acts/Utilities/AnnealingUtility.hpp>
The annealing state Resetting the state is done by just creating a new instance.
Public Members
-
unsigned int currentTemperatureIndex = {0}
-
bool equilibriumReached = {false}
-
unsigned int currentTemperatureIndex = {0}
-
void anneal(State &state) const
-
class AnnulusBounds : public Acts::DiscBounds
- #include <Acts/Surfaces/AnnulusBounds.hpp>
Class that implements a (potentially asymmetric) bounds with difference between surface bound center and surface coordinate center.
These bounds combine two different systems:
module system : radial bounds centred on the moduleOrigin
strip system : phi bounds centred on the stripOrigin
The measurement will be done in the strip system, with r/phi local coordinates.
Public Types
-
enum BoundValues
Values:
-
enumerator eMinR
-
enumerator eMaxR
-
enumerator eMinPhiRel
-
enumerator eMaxPhiRel
-
enumerator eAveragePhi
-
enumerator eOriginX
-
enumerator eOriginY
-
enumerator eSize
-
enumerator eMinR
Public Functions
-
AnnulusBounds() = delete
-
AnnulusBounds(const AnnulusBounds &source) = default
-
AnnulusBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor - from parameters array.
- Parameters
values – The parameter array
-
inline AnnulusBounds(double minR, double maxR, double minPhiRel, double maxPhiRel, const Vector2 &moduleOrigin = {0, 0}, double avgPhi = 0) noexcept(false)
Default constructor from parameters.
Note
For
moriginyou need to actually calculate the cartesian offset- Parameters
minR – inner radius, in module system
maxR – outer radius, in module system
minPhiRel – right angular edge, in strip system, rel to avgPhi
maxPhiRel – left angular edge, in strip system, rel to avgPhi
moduleOrigin – The origin offset between the two systems.
avgPhi – (Optional) internal rotation of this bounds object’s local frame
-
inline virtual double binningValuePhi() const final
Return a reference radius for binning.
-
inline virtual double binningValueR() const final
Return a reference radius for binning.
-
std::vector<Vector2> corners() const
This method returns the four corners of the bounds in polar coordinates Starting from the upper right (max R, pos locX) and proceeding clock-wise i.e.
(max R; pos locX), (min R; pos locX), (min R; neg loc X), (max R: neg locX)
-
inline virtual bool coversFullAzimuth() const final
Returns true for full phi coverage.
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck) const final
Inside check for the bounds object driven by the boundary check directive Each Bounds has a method inside, which checks if a LocalPosition is inside the bounds Inside can be called without/with tolerances.
- Parameters
lposition – Local position (assumed to be in right surface frame)
bcheck – boundary check directive
- Returns
boolean indicator for the success of this operation
-
inline virtual bool insideRadialBounds(double R, double tolerance = 0.) const final
Checks if this is inside the radial coverage given the a tolerance.
-
Vector2 moduleOrigin() const
Returns moduleOrigin, but rotated out, so
averagePhiis already considered.The module origin needs to consider the rotation introduced by
averagePhi- Returns
The origin of the local frame
-
inline double phiMax() const
Returns the left angular edge of the module.
- Returns
The left side angle
-
inline double phiMin() const
Returns the right angular edge of the module.
- Returns
The right side angle
-
inline virtual double rMax() const final
This method returns outer radius.
-
inline virtual double rMin() const final
This method returns inner radius.
-
virtual std::ostream &toStream(std::ostream &sl) const final
Outstream operator.
- Parameters
sl – is the ostream to be dumped into
-
inline virtual SurfaceBounds::BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
virtual std::vector<Vector2> vertices(unsigned int lseg) const override
This method returns the xy coordinates of the four corners of the bounds in module coorindates (in x/y) Starting from the upper right (max R, pos locX) and proceeding clock-wise i.e.
(max R; pos locX), (min R; pos locX), (min R; neg loc X), (max R: neg locX)
Note
that that if
lseg> 0, the extrema points are given, which may slightly alter the number of segments returned- Parameters
lseg – the number of segments used to approximate and eventually curved line
- Returns
vector for vertices in 2D
-
template<size_t SIZE>
class AnyBase : public Acts::AnyBaseAll - #include <Acts/Utilities/Any.hpp>
Small opaque cache type which uses small buffer optimization.
Public Functions
-
AnyBase() = default
-
inline AnyBase(AnyBase &&other)
-
inline AnyBase(const AnyBase &other)
-
template<typename T, typename ...Args>
inline explicit AnyBase(std::in_place_type_t<T>, Args&&... args)
-
template<typename T, typename = std::enable_if_t<!std::is_same_v<std::decay_t<T>, AnyBase<SIZE>>>>
inline explicit AnyBase(T &&value)
-
inline ~AnyBase()
-
template<typename T>
inline T &as()
-
template<typename T>
inline const T &as() const
-
inline operator bool() const
-
AnyBase() = default
-
class AnyBaseAll
- #include <Acts/Utilities/Any.hpp>
Subclassed by Acts::AnyBase< ACTS_SOURCELINK_SBO_SIZE >, Acts::AnyBase< SIZE >
-
class AnyCharge
- #include <Acts/EventData/Charge.hpp>
Charge and momentum interpretation for arbitrarily charged particles.
Only a charge magnitude identical to zero is interpreted as representing a neutral particle. This avoids ambiguities that might arise from using an approximate comparison with an arbitrary epsilon.
Public Functions
-
inline constexpr AnyCharge(float absQ) noexcept
Construct with the magnitude of the input charge.
-
inline constexpr AnyCharge(Neutral) noexcept
-
inline constexpr AnyCharge(SinglyCharged) noexcept
-
inline constexpr float absQ() const noexcept
-
template<typename T>
inline constexpr auto extractCharge(T qOverP) const noexcept
-
template<typename T>
inline constexpr auto extractMomentum(T qOverP) const noexcept
Friends
- inline friend constexpr friend bool operator== (AnyCharge lhs, AnyCharge rhs) noexcept
Compare for equality.
-
inline constexpr AnyCharge(float absQ) noexcept
-
class ApproachDescriptor
- #include <Acts/Geometry/ApproachDescriptor.hpp>
Virtual base class to decide and return which approaching surface to be taken, the surfaces are std::shared_ptr, as they can be the boundary surfaces of the representingVolume of the Layer.
Subclassed by Acts::GenericApproachDescriptor
Public Functions
-
ApproachDescriptor() = default
-
virtual ~ApproachDescriptor() = default
-
virtual ObjectIntersection<Surface> approachSurface(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck) const = 0
Get the surface on approach.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the position from start of the search
direction – is the direction at the start of the search
bcheck – is the boundary check directive
- Returns
is a surface intersection
-
virtual const std::vector<const Surface*> &containedSurfaces() const = 0
Get all the contained surfaces.
- Returns
all contained surfaces of this approach descriptor
-
virtual std::vector<const Surface*> &containedSurfaces() = 0
Non-const version.
-
virtual void registerLayer(const Layer &lay) = 0
Register Layer Links the layer to the approach surfaces.
- Parameters
lay – is the layer to be assigned
-
ApproachDescriptor() = default
-
class AssertionFailureException : public std::exception
- #include <Acts/Utilities/ThrowAssert.hpp>
Exception type for assertion failures This class captures the information available to the throw_assert macro.
Public Functions
-
inline AssertionFailureException(const std::string &expression, const std::string &file, int line, const std::string &msg)
Construct an assertion failure exception, captures macro info.
- Parameters
expression – The expression being asserted
file – The current file
line – The current line
msg – The message to print if assertion fails
-
inline const char *what() const override
The assertion message.
-
class StreamFormatter
- #include <Acts/Utilities/ThrowAssert.hpp>
Class which allows to use the << operator to assemble a string.
Public Functions
-
template<typename T>
inline StreamFormatter &operator<<(const T &value) Stream operator which takes everything and forwards it to the stringstream.
- Template Parameters
T – type of anything
- Parameters
value – const ref to anything
-
template<typename T>
-
inline AssertionFailureException(const std::string &expression, const std::string &file, int line, const std::string &msg)
-
class AtlasStepper
- #include <Acts/Propagator/AtlasStepper.hpp>
the AtlasStepper implementation for the
Public Types
-
using BoundState = std::tuple<BoundTrackParameters, Jacobian, double>
-
using Covariance = BoundSquareMatrix
-
using CurvilinearState = std::tuple<CurvilinearTrackParameters, Jacobian, double>
-
using Jacobian = BoundMatrix
Public Functions
-
inline double absoluteMomentum(const State &state) const
-
inline Result<BoundState> boundState(State &state, const Surface &surface, bool transportCov = true, const FreeToBoundCorrection &freeToBoundCorrection = FreeToBoundCorrection(false)) const
Create and return the bound state at the current position.
- Parameters
state – [in] State that will be presented as
BoundStatesurface – [in] The surface to which we bind the state
transportCov – [in] Flag steering covariance transport
freeToBoundCorrection – [in] Correction for non-linearity effect during transform from free to bound
- Returns
A bound state:
the parameters at the surface
the stepwise jacobian towards it
and the path length (from start - for ordering)
-
inline double charge(const State &state) const
Charge access.
-
inline CurvilinearState curvilinearState(State &state, bool transportCov = true) const
Create and return a curvilinear state at the current position.
- Parameters
state – [in] State that will be presented as
CurvilinearStatetransportCov – [in] Flag steering covariance transport
- Returns
A curvilinear state:
the curvilinear parameters at given position
the stepweise jacobian towards it
and the path length (from start - for ordering)
-
inline Result<Vector3> getField(State &state, const Vector3 &pos) const
Get the field for the stepping It checks first if the access is still within the Cell, and updates the cell if necessary, then it takes the field from the cell.
- Parameters
state – [inout] is the stepper state associated with the track the magnetic field cell is used (and potentially updated)
pos – [in] is the field position
-
inline double getStepSize(const State &state, ConstrainedStep::Type stype) const
Get the step size.
- Parameters
state – [in] The stepping state (thread-local cache)
stype – [in] The step size type to be returned
-
template<typename charge_t>
inline State makeState(std::reference_wrapper<const GeometryContext> gctx, std::reference_wrapper<const MagneticFieldContext> mctx, const GenericBoundTrackParameters<charge_t> &par, double ssize = std::numeric_limits<double>::max(), double stolerance = s_onSurfaceTolerance) const
-
inline std::string outputStepSize(const State &state) const
Output the Step Size - single component.
- Parameters
state – [inout] The stepping state (thread-local cache)
-
inline double overstepLimit(const State&) const
Overstep limit.
-
inline double qOverP(const State &state) const
-
inline void releaseStepSize(State &state) const
Release the Step size.
- Parameters
state – [inout] The stepping state (thread-local cache)
-
inline void resetState(State &state, const BoundVector &boundParams, const BoundSquareMatrix &cov, const Surface &surface, const double stepSize = std::numeric_limits<double>::max()) const
Resets the state.
- Parameters
state – [inout] State of the stepper
boundParams – [in] Parameters in bound parametrisation
cov – [in] Covariance matrix
surface – [in] Reset state will be on this surface
stepSize – [in] Step size
-
inline void setIdentityJacobian(State &state) const
Method that reset the Jacobian to the Identity for when no bound state are available.
- Parameters
state – [inout] State of the stepper
-
inline void setStepSize(State &state, double stepSize, ConstrainedStep::Type stype = ConstrainedStep::actor, bool release = true) const
Set Step size - explicitly with a double.
- Parameters
state – [inout] The stepping state (thread-local cache)
stepSize – [in] The step size value
stype – [in] The step size type to be set
release – [in] Do we release the step size?
Perform the actual step on the state.
- Parameters
state – is the provided stepper state (caller keeps thread locality)
-
inline double time(const State &state) const
Time access.
-
inline void transportCovarianceToBound(State &state, const Surface &surface, const FreeToBoundCorrection& = FreeToBoundCorrection(false)) const
Method for on-demand transport of the covariance to a new curvilinear frame at current position, or direction of the state.
- Parameters
state – [inout] State of the stepper
surface – [in] is the surface to which the covariance is forwarded to
-
inline void transportCovarianceToCurvilinear(State &state) const
Method for on-demand transport of the covariance to a new curvilinear frame at current position, or direction of the state.
- Parameters
state – [inout] State of the stepper
-
inline void update(State &state, const FreeVector ¶meters, const BoundVector &boundParams, const Covariance &covariance, const Surface &surface) const
The state update method.
- Parameters
state – [inout] The stepper state for
parameters – [in] The new free track parameters at start
boundParams – [in] Corresponding bound parameters
covariance – [in] The updated covariance matrix
surface – [in] The surface used to update the pVector
-
inline void update(State &state, const Vector3 &uposition, const Vector3 &udirection, double qop, double time) const
Method to update momentum, direction and p.
- Parameters
state – The state object
uposition – the updated position
udirection – the updated direction
qop – the updated momentum value
time – the update time
-
template<typename object_intersection_t>
inline void updateStepSize(State &state, const object_intersection_t &oIntersection, bool release = true) const Update step size.
It checks the status to the reference surface & updates the step size accordingly
- Parameters
state – [in,out] The stepping state (thread-local cache)
oIntersection – [in] The ObjectIntersection to layer, boundary, etc
release – [in] boolean to trigger step size release
-
inline Intersection3D::Status updateSurfaceStatus(State &state, const Surface &surface, Direction navDir, const BoundaryCheck &bcheck, ActsScalar surfaceTolerance = s_onSurfaceTolerance, const Logger &logger = getDummyLogger()) const
Update surface status.
This method intersect the provided surface and update the navigation step estimation accordingly (hence it changes the state). It also returns the status of the intersection to trigger onSurface in case the surface is reached.
- Parameters
state – [inout] The stepping state (thread-local cache)
surface – [in] The surface provided
navDir – [in] The navigation direction
bcheck – [in] The boundary check for this status update
surfaceTolerance – [in] Surface tolerance used for intersection
logger – [in] Logger instance to use
-
struct State
- #include <Acts/Propagator/AtlasStepper.hpp>
Nested State struct for the local caching.
Public Functions
-
State() = delete
Default constructor - deleted.
-
template<typename Parameters>
inline State(const GeometryContext &gctx, MagneticFieldProvider::Cache fieldCacheIn, const Parameters &pars, double ssize = std::numeric_limits<double>::max(), double stolerance = s_onSurfaceTolerance) Constructor.
- Template Parameters
Type – of TrackParameters
- Parameters
gctx – [in] The geometry context tof this call
fieldCacheIn – [in] The magnetic field cache for this call
pars – [in] Input parameters
ssize – [in] the steps size limitation
stolerance – [in] is the stepping tolerance
Public Members
-
double absCharge = UnitConstants::e
The absolute charge as the free vector can be 1/p or q/p.
-
Covariance cov = Covariance::Zero()
-
const Covariance *covariance = nullptr
-
bool covTransport = false
-
bool debug = false
Debug output the string where debug messages are stored (optionally)
-
size_t debugMsgWidth = 50
-
size_t debugPfxWidth = 30
buffer & formatting for consistent output
-
std::string debugString = ""
-
Vector3 field
-
MagneticFieldProvider::Cache fieldCache
It caches the current magnetic field cell and stays (and interpolates) within as long as this is valid.
See step() code for details.
-
std::reference_wrapper<const GeometryContext> geoContext
Cache the geometry context.
-
double jacobian[eBoundSize * eBoundSize] = {}
-
double maxPathLength = 0
-
bool mcondition = false
-
bool needgradient = false
-
bool newfield = true
-
double parameters[eBoundSize] = {0., 0., 0., 0., 0., 0.}
Storage pattern of pVector /dL0 /dL1 /dPhi /the /dCM /dT X ->P[0] dX / P[ 8] P[16] P[24] P[32] P[40] P[48] Y ->P[1] dY / P[ 9] P[17] P[25] P[33] P[41] P[49] Z ->P[2] dZ / P[10] P[18] P[26] P[34] P[42] P[50] T ->P[3] dT/ P[11] P[19] P[27] P[35] P[43] P[51] Ax ->P[4] dAx/ P[12] P[20] P[28] P[36] P[44] P[52] Ay ->P[5] dAy/ P[13] P[21] P[29] P[37] P[45] P[53] Az ->P[6] dAz/ P[14] P[22] P[30] P[38] P[46] P[54] CM ->P[7] dCM/ P[15] P[23] P[31] P[39] P[47] P[55] Cache: P[56] - P[59].
-
double pathAccumulated = 0.
-
double previousStepSize = 0.
-
std::array<double, 60> pVector = {}
-
bool state_ready = false
-
double step = 0
-
ConstrainedStep stepSize
-
double tolerance = s_onSurfaceTolerance
The tolerance for the stepping.
-
bool useJacobian = false
-
State() = delete
-
using BoundState = std::tuple<BoundTrackParameters, Jacobian, double>
-
template<template<typename> typename basic_extension_t>
struct AutodiffExtensionWrapper - #include </home/docs/checkouts/readthedocs.org/user_builds/acts/checkouts/v29.0.0/Plugins/Autodiff/include/Acts/Plugins/Autodiff/AutodiffExtensionWrapper.hpp>
Default RKN4 evaluator for autodiff.
Public Types
-
using AutodiffFreeMatrix = Eigen::Matrix<AutodiffScalar, eFreeSize, eFreeSize>
-
using AutodiffFreeVector = Eigen::Matrix<AutodiffScalar, eFreeSize, 1>
-
using AutodiffScalar = autodiff::dual
-
using AutodiffVector3 = Eigen::Matrix<AutodiffScalar, 3, 1>
Public Functions
-
AutodiffExtensionWrapper() = default
Default constructor.
Public Members
-
basic_extension_t<double> m_doubleExtension
-
using AutodiffFreeMatrix = Eigen::Matrix<AutodiffScalar, eFreeSize, eFreeSize>
-
template<typename entity_t, typename value_t, size_t DIM>
class AxisAlignedBoundingBox - #include <Acts/Utilities/BoundingBox.hpp>
Implementation of an Axis Aligned Bounding Box.
This type is compatible with 2D and 3D boxes
Public Types
-
using entity_type = entity_t
Type of stored entity.
-
using Size = NamedType<VertexType, struct SizeParameter>
Strong type to select the correct constructor.
-
using transform_type = Eigen::Transform<value_type, DIM, Eigen::Affine>
The transform type based on the
value_type
-
using value_type = value_t
The value type used by this class.
Public Functions
-
AxisAlignedBoundingBox(const entity_t *entity, const VertexType ¢er, const Size &size)
Constructor from a center position, and a width and height.
Note
The special type
sizeis required to disambiguate this constructor from the other one above. It is a wrapper around a simpleVector3.- Parameters
entity – The entity to store
center – The center position
size – The size (width and height) of the box.
-
AxisAlignedBoundingBox(const entity_t *entity, const VertexType &vmin, const VertexType &vmax)
Constructor from an entity pointer, and the min and max vertices.
- Parameters
entity – The entity to store
vmin – The minimum vertex.
vmax – The maximum vertex.
-
AxisAlignedBoundingBox(const self_t &other) = default
Copy constructor from other bounding box.
- Parameters
other – The other AABB
-
AxisAlignedBoundingBox(const std::vector<self_t*> &boxes, vertex_array_type envelope = vertex_array_type::Zero())
Constructor from a list of child boxes.
This box will wrap around all boxes contained in
boxes, and additional envelope can be given.- Parameters
boxes – Vector of child boxes to store in this bounding box.
envelope – Envelope that will be added/subtracted to the dimension.
-
const VertexType ¢er() const
Get the center position of this bounding box.
- Returns
The center position
-
template<size_t D = DIM, std::enable_if_t<D == 3, int> = 0>
void draw(IVisualization3D &helper, std::array<int, 3> color = {120, 120, 120}, const transform_type &trf = transform_type::Identity()) const Draw this bounding box using the given visualization helper.
This method is only available for the 3D case.
- Template Parameters
D – (used for SFINAE)
- Parameters
helper – The visualization helper to write to
color – The color to use for drawing
trf – An optional transform to apply first.
-
const entity_t *entity() const
Return the entity associated with this box.
This might be nullptr if there is no entity attached.
- Returns
The entity pointer, might be nullptr
-
const self_t *getLeftChild() const
Get the left child (i.e.
the first of the children that are inside this bounding box).
- Returns
The lest most child.
-
const self_t *getSkip() const
Get the skip node for this box.
- Returns
The skip node pointer
-
bool hasEntity() const
Check whether this node as an associated entity.
If it does not have one, this is a purely abstract container box.
- Returns
Whether the box has an entity attached.
-
template<size_t sides>
bool intersect(const Frustum<value_type, DIM, sides> &fr) const Check if a frustum intersects with this bounding box.
This method implements an algorithm similar to the one described in “Optimized View Frustum Culling Algorithms for Bounding Boxes (2012)” 2, but drops some of the more sophisticated optimization.
- Parameters
fr – The frustum
- Returns
Whether the frustum intersects this AABB
-
bool intersect(const Ray<value_type, DIM> &ray) const
Implements the slab method for Ray/AABB intersections.
See https://tavianator.com/fast-branchless-raybounding-box-intersections/, https://tavianator.com/fast-branchless-raybounding-box-intersections-part-2-nans/, https://medium.com/@bromanz/another-view-on-the-classic-ray-aabb-intersection-algorithm-for-bvh-traversal-41125138b525 The original algorithms is described in “Graphics Gems (1990)” 1
Note
This implementation may treat parallel rays on any of the slabs as outside due to how
NaNsare handled by Eigen. See http://eigen.tuxfamily.org/bz/show_bug.cgi?id=564- Parameters
ray – The ray to intersect with
- Returns
Whether the ray intersects this AABB
-
bool intersect(const VertexType &point) const
Calculate whether a point is inside this box.
- Parameters
point – The point to test.
- Returns
Whether the point is inside or not.
-
const VertexType &max() const
Get the maximum vertex.
- Returns
The maximum vertex
-
const VertexType &min() const
Get the minimum vertex.
- Returns
The minimum vertex
-
AxisAlignedBoundingBox &operator=(const self_t &other) = default
Copy assignment operator from other bounding box.
- Parameters
other – The other AABB
-
void setEntity(const entity_t *entity)
Set the entity associated with with this box.
- Parameters
entity – The entity
-
void setSkip(self_t *skip)
Set the skip node (bounding box)
- Parameters
skip – The target skip node pointer
-
template<size_t D = DIM, std::enable_if_t<D == 2, int> = 0>
std::ostream &svg(std::ostream &os, value_type w, value_type h, value_type unit = 10, const std::string &label = "", const std::string &fillcolor = "grey") const Draw this bounding box as SVG.
This method is only available for the 2D case.
- Template Parameters
D – (used for SFINAE)
- Parameters
os – The output stream to write to
w – The width of the output SVG.
h – The height of the output SVG.
unit – A scale factor to apply before drawing
label – A label to put next to the box.
fillcolor – Color to fill the box with.
- Returns
The outstream given in
os.
-
std::ostream &toStream(std::ostream &os) const
Write information about this bounding box to a stream.
- Parameters
os – The output stream.
- Returns
The stream given as an argument.
-
void transform(const transform_type &trf)
Transforms this bounding box using the given transform.
This method modifies the box it is called on.
- Parameters
trf – The transform
-
self_t transformed(const transform_type &trf) const
Transforms this bounding box using the given transform.
This method returns a copy of this box, with the transformation applied, and leaves this instance unchanged.
- Parameters
trf – The transform
- Returns
The transformed bounding box
Public Static Functions
-
static std::pair<VertexType, VertexType> wrap(const std::vector<const self_t*> &boxes, vertex_array_type envelope = vertex_array_type::Zero())
Helper function to calculate the size of a bounding box enclosing
boxes.- Parameters
boxes – The boxes to wrap (const pointers)
envelope – Optional envelop to add/subtract to dimension.
- Returns
Pair of vertices: min and max.
-
static std::pair<VertexType, VertexType> wrap(const std::vector<self_t*> &boxes, vertex_array_type envelope = vertex_array_type::Zero())
Helper function to calculate the size of a bounding box enclosing
boxes.Overload which accepts non-const boxes in
boxes.- Parameters
boxes – The boxes to wrap (non-const pointers)
envelope – Optional envelop to add/subtract to dimension.
- Returns
Pair of vertices: min and max.
-
static std::pair<VertexType, VertexType> wrap(const std::vector<self_t> &boxes, vertex_array_type envelope = vertex_array_type::Zero())
Helper function to calculate the size of a bounding box enclosing
boxes.Overload which accepts a vector in
boxeswhich owns the instances- Parameters
boxes – The boxes to wrap (by-value vector)
envelope – Optional envelop to add/subtract to dimension.
- Returns
Pair of vertices: min and max.
Public Static Attributes
-
static const size_t dim = DIM
Re-export dimension from template parameter.
-
using entity_type = entity_t
-
template<typename external_spacepoint_t>
class BinFinder - #include <Acts/Seeding/BinFinder.hpp>
The BinFinder is used by the ISPGroupSelector.
It can be used to find both bins that could be bottom bins as well as bins that could be top bins, which are assumed to be the same bins. Does not take interaction region into account to limit z-bins.
Public Functions
-
BinFinder() = delete
constructor
-
BinFinder(const std::vector<std::pair<int, int>> &zBinNeighbors, int numPhiNeighbors)
-
boost::container::small_vector<size_t, 9> findBins(size_t phiBin, size_t zBin, const SpacePointGrid<external_spacepoint_t> *binnedSP) const
Return all bins that could contain space points that can be used with the space points in the bin with the provided indices to create seeds.
- Parameters
phiBin – phi index of bin with middle space points
zBin – z index of bin with middle space points
binnedSP – phi-z grid containing all bins
-
BinFinder() = delete
-
template<class T>
class BinnedArray - #include <Acts/Utilities/BinnedArray.hpp>
Pure virtual base class for Binned Array to avoid map searches.
there is only one restriction: T must be of pointer type in order to be initialized with nullptr and to allow for nullptr return type
the BinnedArray is designed for 0D, 1D, 2D, and 3D binning
Subclassed by Acts::BinnedArrayXD< T >
Public Functions
-
BinnedArray() = default
Default Constructor - needed for inherited classes.
-
virtual ~BinnedArray() = default
Virtual Destructor.
-
virtual const std::vector<T> &arrayObjects() const = 0
Return all unique object.
Note
this is the accessor to the
- Returns
the vector of all array objects
-
virtual const BinUtility *binUtility() const = 0
Return the BinUtility.
if returned 0 it is a 0D array
- Returns
plain pointer to the bin utility
-
inline virtual T object(const Vector2 &lposition) const
Same method without bins for backward compatibility.
- Parameters
lposition – is the local position for finding the object
- Returns
the object according to the estimated bin
-
virtual T object(const Vector2 &lposition, std::array<size_t, 3> &bins) const = 0
Returns the object in the associated bin according the local position.
- Parameters
lposition – is the local position for the object retrieval
bins – is the bin triple to filled
- Returns
the object according to the estimated bin
-
inline virtual T object(const Vector3 &position) const
Same method without bins for backward compatibility.
- Parameters
position – is the global position for the object finding
- Returns
the object according to the estimated bin
-
virtual T object(const Vector3 &position, std::array<size_t, 3> &bin) const = 0
Returns the object in the associated bin according the local position.
- Parameters
position – is the global position for the object retrieval
bin – is the bin triple filled
- Returns
the object according to the estimated bin
-
virtual const std::vector<std::vector<std::vector<T>>> &objectGrid() const = 0
Return the object grid multiple entries are allowed.
- Returns
the object grid
-
template<class T>
class BinnedArrayXD : public Acts::BinnedArray<T> - #include <Acts/Utilities/BinnedArrayXD.hpp>
Avoiding a map search, the templated BinnedArray class can help ordereing geometrical objects by providing a dedicated BinUtility.
This can be 0D, 1D, 2D, and 3D in regular binning
the type of Binning is given defined through the BinUtility
Public Functions
-
BinnedArrayXD(const BinnedArrayXD<T> &barr) = delete
Copy constructor.
not allowed, use the same array
-
inline BinnedArrayXD(const std::vector<std::vector<std::vector<T>>> &grid, std::unique_ptr<const BinUtility> bu)
Constructor with a grid and a BinUtility.
- Parameters
grid – is the prepared object grid
bu – is the unique bin utility for this binned array
-
inline BinnedArrayXD(const std::vector<TAP> &tapvector, std::unique_ptr<const BinUtility> bu)
Constructor with std::vector and a BinUtility.
fills the internal data structure
- Parameters
tapvector – is a vector of object and binning position
bu – is the unique bin utility for this binned array
-
inline BinnedArrayXD(T object)
Constructor for single object.
- Template Parameters
object – is the single object
-
~BinnedArrayXD() override = default
Destructor.
-
inline virtual const std::vector<T> &arrayObjects() const final
Return all unique object.
- Returns
vector of unique array objects
-
inline virtual const BinUtility *binUtility() const final
Return the BinUtility.
- Returns
plain pointer to the bin utility of this array
-
inline virtual T object(const Vector2 &lposition) const override
Same method without bins for backward compatibility.
- Parameters
lposition – is the local position for finding the object
- Returns
the object according to the estimated bin
-
inline virtual T object(const Vector2 &lposition, std::array<size_t, 3> &bins) const final
Returns the object in the array from a local position.
- Parameters
lposition – is the local position for the bin search
bins – is the bin triple filled during this access
- Returns
is the object in that bin
-
inline virtual T object(const Vector3 &position) const override
Same method without bins for backward compatibility.
- Parameters
position – is the global position for the object finding
- Returns
the object according to the estimated bin
-
inline virtual T object(const Vector3 &position, std::array<size_t, 3> &bins) const final
Returns the object in the array from a global position.
- Parameters
position – is the global position for the bin search
bins – is the bins triple filled during access
- Returns
is the object in that bin
-
inline virtual const std::vector<std::vector<std::vector<T>>> &objectGrid() const final
Return the object grid multiple entries are allowed and wanted.
- Returns
internal object grid
-
BinnedArrayXD &operator=(const BinnedArrayXD<T> &barr) = delete
Assignment operator.
not allowed, use the same array
-
BinnedArrayXD(const BinnedArrayXD<T> &barr) = delete
-
template<typename external_spacepoint_t>
class BinnedSPGroup - #include <Acts/Seeding/BinnedSPGroup.hpp>
BinnedSPGroupProvides access to begin and end BinnedSPGroupIterator for given BinFinders and SpacePointGrid.Fulfills the range_expression interface.
Public Functions
-
BinnedSPGroup() = delete
-
BinnedSPGroup(BinnedSPGroup&&) noexcept = default
-
BinnedSPGroup(const BinnedSPGroup&) = delete
-
~BinnedSPGroup() = default
-
inline Acts::SpacePointGrid<external_spacepoint_t> &grid()
-
BinnedSPGroup &operator=(BinnedSPGroup&&) noexcept = default
-
BinnedSPGroup &operator=(const BinnedSPGroup&) = delete
-
size_t size() const
-
inline std::size_t skipZMiddleBin()
-
BinnedSPGroup() = delete
-
template<typename external_spacepoint_t>
class BinnedSPGroupIterator - #include <Acts/Seeding/BinnedSPGroup.hpp>
BinnedSPGroupIteratorAllows to iterate over all groups of bins a provided BinFinder can generate for each bin of a provided SPGridSpacePointGrid is a very specific structure. We know it is 2D and what it contains No need to be too general with this class
Public Functions
-
BinnedSPGroupIterator(BinnedSPGroup<external_spacepoint_t> &&group, std::size_t) = delete
-
BinnedSPGroupIterator(BinnedSPGroup<external_spacepoint_t> &group, std::size_t index)
-
BinnedSPGroupIterator(BinnedSPGroupIterator&&) noexcept = default
-
BinnedSPGroupIterator(const BinnedSPGroupIterator&) = delete
-
~BinnedSPGroupIterator() = default
-
bool operator!=(const BinnedSPGroupIterator &other) const
-
std::tuple<boost::container::small_vector<size_t, 9>, std::size_t, boost::container::small_vector<size_t, 9>> operator*() const
-
BinnedSPGroupIterator &operator++()
-
BinnedSPGroupIterator &operator=(BinnedSPGroupIterator&&) noexcept = default
-
BinnedSPGroupIterator &operator=(const BinnedSPGroupIterator&) = delete
-
bool operator==(const BinnedSPGroupIterator &other) const
-
BinnedSPGroupIterator(BinnedSPGroup<external_spacepoint_t> &&group, std::size_t) = delete
-
class BinnedSurfaceMaterial : public Acts::ISurfaceMaterial
- #include <Acts/Material/BinnedSurfaceMaterial.hpp>
It extends the
ISurfaceMaterialbase class and is an array pf MaterialSlab.This is not memory optimised as every bin holds one material property object.
Public Functions
-
BinnedSurfaceMaterial() = delete
Default Constructor - deleted.
-
BinnedSurfaceMaterial(BinnedSurfaceMaterial &&bsm) = default
Copy Move Constructor.
- Parameters
bsm – is the source object to be copied
-
BinnedSurfaceMaterial(const BinnedSurfaceMaterial &bsm) = default
Copy Constructor.
- Parameters
bsm – is the source object to be copied
-
BinnedSurfaceMaterial(const BinUtility &binUtility, MaterialSlabMatrix fullProperties, double splitFactor = 0., MappingType mappingType = MappingType::Default)
Explicit constructor with only full MaterialSlab, for two-dimensional binning.
The split factors:
1. : oppositePre
0. : alongPre ===> 1 Dimensional array
- Parameters
binUtility – defines the binning structure on the surface (copied)
fullProperties – is the vector of properties as recorded (moved)
splitFactor – is the pre/post splitting directive
mappingType – is the type of surface mapping associated to the surface
-
BinnedSurfaceMaterial(const BinUtility &binUtility, MaterialSlabVector fullProperties, double splitFactor = 0., MappingType mappingType = MappingType::Default)
Explicit constructor with only full MaterialSlab, for one-dimensional binning.
The split factors:
1. : oppositePre
0. : alongPre ===> 1 Dimensional array
- Parameters
binUtility – defines the binning structure on the surface (copied)
fullProperties – is the vector of properties as recorded (moved)
splitFactor – is the pre/post splitting directive
mappingType – is the type of surface mapping associated to the surface
-
~BinnedSurfaceMaterial() override = default
Destructor.
-
inline const BinUtility &binUtility() const
Return the BinUtility.
-
inline const MaterialSlabMatrix &fullMaterial() const
Retrieve the entire material slab matrix.
-
virtual const MaterialSlab &materialSlab(const Vector2 &lp) const final
Return method for full material description of the Surface.
from local coordinate on the surface
- Parameters
lp – is the local position used for the (eventual) lookup
- Returns
const MaterialSlab
-
virtual const MaterialSlab &materialSlab(const Vector3 &gp) const final
Return method for full material description of the Surface.
from the global coordinates
- Parameters
gp – is the global position used for the (eventual) lookup
- Returns
const MaterialSlab
-
inline virtual const MaterialSlab &materialSlab(size_t bin0, size_t bin1) const final
Direct access via bins to the MaterialSlab.
- Parameters
bin0 – is the material bin in dimension 0
bin1 – is the material bin in dimension 1
-
virtual BinnedSurfaceMaterial &operator*=(double scale) final
Scale operator.
- Parameters
scale – is the scale factor for the full material
-
BinnedSurfaceMaterial &operator=(BinnedSurfaceMaterial &&bsm) = default
Assignment Move operator.
-
BinnedSurfaceMaterial &operator=(const BinnedSurfaceMaterial &bsm) = default
Assignment operator.
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream, to be overloaded by child classes.
-
BinnedSurfaceMaterial() = delete
-
class BinningData
- #include <Acts/Utilities/BinningData.hpp>
This class holds all the data necessary for the bin calculation.
phi has a very particular behaviour:
there’s the change around +/- PI
it can be multiplicative or additive multiplicative : each major bin has the same sub structure i.e. first binnning
structure is equidistant additive : sub structure replaces one bin (and one bin only)
Public Functions
-
BinningData() = default
-
inline BinningData(BinningOption bOption, BinningValue bValue, const std::vector<float> &bBoundaries, std::unique_ptr<const BinningData> sBinData = nullptr)
Constructor for non-equidistant binning.
- Parameters
bOption – is the binning option : open / closed
bValue – is the binning value : binX, binY, etc.
bBoundaries – are the bin boundaries
sBinData – is (optional) sub structure
-
inline BinningData(BinningOption bOption, BinningValue bValue, size_t bBins, float bMin, float bMax, std::unique_ptr<const BinningData> sBinData = nullptr, bool sBinAdditive = false)
Constructor for equidistant binning and optional sub structure can be multiplicative or additive.
- Parameters
bOption – is the binning option : open, closed
bValue – is the binning value: binX, binY, etc.
bBins – is number of equidistant bins
bMin – is the minimum value
bMax – is the maximum value
sBinData – is (optional) sub structure
sBinAdditive – is the prescription for the sub structure
-
inline BinningData(BinningValue bValue, float bMin, float bMax)
Constructor for 0D binning.
- Parameters
bValue – is the binning value: binX, binY, etc.
bMin – is the minimum value
bMax – is the maximum value
-
inline BinningData(const BinningData &bdata)
Copy constructor.
- Parameters
bdata – is the source object
-
~BinningData() = default
-
inline size_t bins() const
Return the number of bins - including sub bins.
-
inline const std::vector<float> &boundaries() const
Return the boundaries - including sub boundaries.
- Returns
vector of floats indicating the boundary values
-
inline float center(size_t bin) const
Get the center value of a bin.
- Parameters
bin – is the bin for which the center value is requested
- Returns
float value according to the bin center
-
inline float centerValue(size_t bin) const
access to the center value this uses the bin boundary vector, it also works with sub structure
- Parameters
bin – is the bin for which the value is requested, if bin > nbins it is set to max
- Returns
the center value of the bin is given
-
inline bool inside(const Vector2 &lposition) const
Check if bin is inside from Vector2.
- Parameters
lposition – is the search position in global coordinated
- Returns
boolean if this is inside() method is true
-
inline bool inside(const Vector3 &position) const
Check if bin is inside from Vector3.
- Parameters
position – is the search position in global coordinated
- Returns
boolean if this is inside() method is true
-
inline int nextDirection(const Vector3 &position, const Vector3 &dir) const
Layer next direction is needed.
- Parameters
position – is the start search position
dir – is the direction
- Returns
integer that indicates which direction to move
-
inline BinningData &operator=(const BinningData &bdata)
Assignment operator.
- Parameters
bdata – is the source object
-
inline bool operator==(const BinningData &bData) const
Equality operator.
- Parameters
bData – is the binning data to be checked against
- Returns
a boolean indicating if they are the same
-
inline size_t search(float value) const
Generic search - forwards to correct function pointer.
- Parameters
value – is the searchvalue as float
- Returns
bin according tot this
-
inline size_t searchGlobal(const Vector3 &position) const
Generic search from a 3D position — corresponds to global coordinate schema.
- Parameters
position – is the search position in global coordinated
- Returns
bin according tot this
-
inline size_t searchLocal(const Vector2 &lposition) const
Generic search from a 2D position — corresponds to local coordinate schema.
- Parameters
lposition – is the search position in local coordinated
- Returns
bin according tot this
-
inline size_t searchWithSubStructure(float value) const
Generic search with sub structure.
forwards to correct function pointer
- Parameters
value – is the searchvalue as float
- Returns
bin according tot this
-
inline std::string toString(const std::string &indent) const
String screen output method.
- Parameters
indent – the current indentation
- Returns
a string containing the screen information
-
inline float value(const Vector2 &lposition) const
Take the right float value.
- Parameters
lposition – assumes the correct local position expression
- Returns
float value according to the binning setup
-
inline float value(const Vector3 &position) const
Take the right float value.
- Parameters
position – is the global position
- Returns
float value according to the binning setup
-
inline float width(size_t bin) const
Get the width of a bin.
- Parameters
bin – is the bin for which the width is requested
- Returns
float value of width
Public Members
-
BinningValue binvalue = {}
binning value: binX, binY, binZ, binR …
-
float max = {}
maximum value
-
float min = {}
minimum value
-
BinningOption option = {}
binning option: open, closed
-
float step = {}
binning step
-
bool subBinningAdditive = {}
sub structure: additive or multipicative
-
std::unique_ptr<const BinningData> subBinningData
sub structure: describe some sub binning
-
BinningType type = {}
binning type: equidistant, arbitrary
-
bool zdim = {}
zero dimensional binning : direct access
-
class BinUtility
- #include <Acts/Utilities/BinUtility.hpp>
The BinUtility class that translated global and local position into a bins of a BinnedArray, most performant is equidistant binning without a transform, however, optionally a transform can be provided, e.g.
for binning on shifted object, the transform is usually shared with the geometric object the Array is defined on, for performance reasons, also the inverse transform is stored.
Public Functions
-
inline BinUtility()
Constructor for equidistant.
-
BinUtility(BinUtility &&sbu) = default
-
inline BinUtility(const BinningData &bData, const Transform3 &tForm = Transform3::Identity())
Constructor from BinningData directly.
- Parameters
bData – is the provided binning data
tForm – is the (optional) transform
-
BinUtility(const BinUtility &sbu) = default
Copy constructor.
- Parameters
sbu – is the source bin utility
-
inline BinUtility(const Transform3 &tForm)
Constructor with only a Transform3.
- Parameters
tForm – is the local to global transform
-
inline BinUtility(size_t bins, float min, float max, BinningOption opt = open, BinningValue value = binX, const Transform3 &tForm = Transform3::Identity())
Constructor for equidistant.
- Parameters
bins – is the number of bins
min – in the minimal value
max – is the maximal value
opt – is the binning option : open, closed
value – is the binninb value : binX, binY, binZ, etc.
tForm – is the (optional) transform
-
inline BinUtility(std::vector<float> &bValues, BinningOption opt = open, BinningValue value = binPhi, const Transform3 &tForm = Transform3::Identity())
Constructor for arbitrary.
- Parameters
bValues – is the boundary values of the binning
opt – is the binning option : open, closed
value – is the binninb value : binX, binY, binZ, etc.
tForm – is the (optional) transform
-
~BinUtility() = default
Virtual Destructor.
-
inline size_t bin(const Vector2 &lposition, size_t ba = 0) const
Bin from a 2D vector (following local parameters defintitions)
no optional transform applied
USE WITH CARE !!
You need to make sure that the local position is actually in the binning frame of the BinUtility
- Parameters
lposition – is the local position to be set
ba – is the bin dimension
- Returns
bin calculated from local
-
inline size_t bin(const Vector3 &position, size_t ba = 0) const
Bin from a 3D vector (already in binning frame)
- Parameters
position – is the 3D position to be evaluated
ba – is the bin dimension
- Returns
is the bin value
-
inline const std::vector<BinningData> &binningData() const
Return the binning data vector.
-
inline BinningValue binningValue(size_t ba = 0) const
The type/value of the binning.
- Parameters
ba – is the binaccessor
- Returns
the binning value of the accessor entry
-
inline size_t bins() const
Return the total number of bins.
-
inline size_t bins(size_t ba) const
Number of bins.
- Parameters
ba – is the binaccessor
- Returns
size_t is the bins of the accessor entry
-
inline std::array<size_t, 3> binTriple(const Vector3 &position) const
Bin-triple fast access.
calculate the bin triple with one transform
- Parameters
position – is the 3D position to be evaluated
- Returns
is the bin value in 3D
-
inline size_t dimensions() const
First bin maximal value.
- Returns
the dimension of the binning data
-
inline bool inside(const Vector2 &lposition) const
Check if bin is inside from Vector2 - no optional transform applied.
- Parameters
lposition – is the local position to be evaluated
- Returns
is a boolean check
-
inline bool inside(const Vector3 &position) const
Check if bin is inside from Vector2 - optional transform applied.
- Parameters
position – is the global position to be evaluated
- Returns
is a boolean check
-
inline size_t max(size_t ba = 0) const
First bin maximal value.
- Parameters
ba – is the binaccessor
- Returns
size_t is the maximal bin of the accessor entry
-
inline int nextDirection(const Vector3 &position, const Vector3 &direction, size_t ba = 0) const
Return the other direction for fast interlinking.
- Parameters
position – is the global position for the next search
direction – is the global position for the next search
ba – is the bin accessor
- Returns
the next bin
-
inline BinUtility &operator+=(const BinUtility &gbu)
Operator+= to make multidimensional BinUtility.
- Parameters
gbu – is the additional BinUtility to be chosen
-
BinUtility &operator=(BinUtility&&) = default
-
inline BinUtility &operator=(const BinUtility &sbu)
Assignment operator.
- Parameters
sbu – is the source bin utility
-
inline bool operator==(const BinUtility &other) const
Equality operator.
-
inline size_t serialize(const std::array<size_t, 3> &bin) const
Serialize the bin triple.
this creates a simple size_t from a triple object
- Parameters
bin – is the bin to be serialized
-
inline std::ostream &toStream(std::ostream &sl, const std::string &indent = "") const
Output Method for std::ostream, to be overloaded by child classes.
- Parameters
sl – is the ostream to be dumped into
indent – the current indentation
- Returns
the input stream
-
inline std::string toString(const std::string &indent = "") const
Output into a string.
- Parameters
indent – the current indentation
- Returns
a string with the stream information
-
inline const Transform3 &transform() const
Transform applied to global positions before lookup.
- Returns
Shared pointer to transform
-
inline BinUtility()
-
class BoostTrackBuilding : public Acts::TrackBuildingBase
- #include <Acts/Plugins/ExaTrkX/BoostTrackBuilding.hpp>
Public Functions
-
inline BoostTrackBuilding(std::unique_ptr<const Logger> logger)
-
virtual std::vector<std::vector<int>> operator()(std::any nodes, std::any edges, std::any edge_weights, std::vector<int> &spacepointIDs) override
Perform track building.
- Parameters
nodes – Node tensor with shape (n_nodes, n_node_features)
edges – Edge-index tensor with shape (2, n_edges)
edgeWeights – Edge-weights of the previous edge classification phase
spacepointIDs – IDs of the nodes (must have size=n_nodes)
- Returns
tracks (as vectors of node-IDs)
-
inline BoostTrackBuilding(std::unique_ptr<const Logger> logger)
-
class BoundaryCheck
- #include <Acts/Surfaces/BoundaryCheck.hpp>
The BoundaryCheck class provides boundary checks and distance calculations for aligned box-like and polygonal boundaries on local surfaces.
Different types of boundary checks are supported and are transparently selected when calling the
isInside(...)anddistance(...)methods:Hard checks w/o any tolerances
Tolerance-based checks in one or in both local coordinates
Chi2-based checks based on a covariance matrix. Non-vanishing correlations are correctly taken into account.
With a defined covariance matrix, the closest point and the distance are not defined along the usual Euclidean metric, but by the Mahalanobis distance induced by the covariance.
Public Types
-
enum class Type
Values:
-
enumerator eNone
disable boundary check
-
enumerator eAbsolute
absolute cut
-
enumerator eChi2
chi2-based cut with full correlations
-
enumerator eNone
Public Functions
-
inline BoundaryCheck(bool check)
Construct either hard cut in both dimensions or no cut at all.
-
inline BoundaryCheck(bool checkLocal0, bool checkLocal1, double tolerance0 = 0, double tolerance1 = 0)
Construct a tolerance based check.
- Parameters
checkLocal0 – Boolean directive to check coordinate 0
checkLocal1 – Boolean directive to check coordinate 1
tolerance0 – Tolerance along coordinate 0
tolerance1 – Tolerance along coordinate 1
-
inline BoundaryCheck(const SquareMatrix2 &localCovariance, double sigmaMax = 1)
Construct a chi2-based check.
- Parameters
localCovariance – Coverance matrix in local coordinates
sigmaMax – Significance for the compatibility test
-
template<typename Vector2Container>
inline Acts::Vector2 computeClosestPointOnPolygon(const Acts::Vector2 &point, const Vector2Container &vertices) const
-
inline SquareMatrix2 covariance() const
-
inline double distance(const Vector2 &point, const Vector2 &lowerLeft, const Vector2 &upperRight) const
Calculate the signed, weighted, closest distance to an aligned box.
If a covariance is defined, the distance is the corresponding Mahalanobis distance. Otherwise, it is the Eucleadian distance.
- Parameters
point – Test point
lowerLeft – Minimal vertex of the box
upperRight – Maximal vertex of the box
- Returns
Negative value if inside, positive if outside
-
template<typename Vector2Container>
inline double distance(const Vector2 &point, const Vector2Container &vertices) const Calculate the signed, weighted, closest distance to a polygonal boundary.
If a covariance is defined, the distance is the corresponding Mahalanobis distance. Otherwise, it is the Eucleadian distance.
- Parameters
point – Test point
vertices – Forward iterable container of convex polygon vertices. Calling
std::begin/std::endon the container must return an iterator where*itmust be convertible to anActs::Vector2.
- Returns
Negative value if inside, positive if outside
-
inline bool isInside(const Vector2 &point, const Vector2 &lowerLeft, const Vector2 &upperRight) const
Check if the point is inside a box aligned with the local axes.
The check takes into account whether tolerances or covariances are defined for the boundary check.
- Parameters
point – Test point
lowerLeft – Minimal vertex of the box
upperRight – Maximal vertex of the box
-
template<typename Vector2Container>
inline bool isInside(const Vector2 &point, const Vector2Container &vertices) const Check if the point is inside a polygon.
The check takes into account whether tolerances or covariances are defined for the boundary check.
- Parameters
point – Test point
vertices – Forward iterable container of convex polygon vertices. Calling
std::begin/std::endon the container must return an iterator where*itmust be convertible to anActs::Vector2.
-
inline operator bool() const
-
inline bool operator!() const
-
inline const Vector2 &tolerance() const
-
inline Type type() const
Broadcast the type.
-
template<class volume_t>
class BoundarySurfaceT - #include <Acts/Geometry/BoundarySurfaceT.hpp>
The boundary surface class combines a Surface with the information of a volume. It’s templated in the type of volume in order to allow for a return type tat is usable in the navigation stream.
Note
along/oppose definitions are given with respect to the normal vector of the boundary surface.
- Template Parameters
volume_t – the type of volume.
Public Functions
-
inline BoundarySurfaceT()
Constructor for a Boundary with exact two Volumes attached to it.
usually used in a volume constructor
- Parameters
surface – The unique surface the boundary represents
inside – The inside volume the boundary surface points to
outside – The outside volume the boundary surface points to
Constructor for a Boundary with exact multiple Volumes attached to it.
usually used in a volume constructor
- Parameters
surface – The unique surface the boundary represents
insideArray – The inside volume array the boundary surface points to
outsideArray – The outside volume array the boundary surface points to
Constructor for a Boundary with exact two Volumes attached to it.
usually used in a volume constructor
- Parameters
surface – The unique surface the boundary represents
inside – The inside volume the boundary surface points to
outside – The outside volume the boundary surface points to
-
virtual ~BoundarySurfaceT() = default
-
virtual const volume_t *attachedVolume(const GeometryContext &gctx, const Vector3 &pos, const Vector3 &mom, Direction dir) const
Get the next Volume depending on GlobalPosition, GlobalMomentum, dir on the TrackParameters and the requested direction.
- Parameters
gctx – The current geometry context object, e.g. alignment
pos – The global position on surface
mom – The direction on the surface
dir – is an additional direction corrective
- Returns
The attached volume at that position
-
void attachVolume(const volume_t *volume, Direction dir)
Helper method: attach a Volume to this BoundarySurfaceT this is done during the geometry construction.
- Parameters
volume – The volume to be attached
dir – The direction for attaching
Helper method: attach a Volume to this BoundarySurfaceT this is done during the geometry construction.
- Parameters
volumes – The volume array to be attached
dir – The direction for attaching
-
template<class parameters_t>
inline bool onBoundary(const GeometryContext &gctx, const parameters_t &pars) const templated onBoundary method
- Template Parameters
parameters_t – are the parameters to be checked
- Parameters
gctx – The current geometry context object, e.g. alignment
pars – The parameters used for this call
-
inline virtual const Surface &surfaceRepresentation() const
The Surface Representation of this.
-
template<typename external_space_point_t>
class CandidatesForMiddleSp - #include <Acts/Seeding/CandidatesForMiddleSp.hpp>
The CandidatesForMiddleSp collects the triplet candidates given a fixed middle spacepoint.
It internally stores the triplet candidates keeping only those with the higher quality.
- Template Parameters
external_space_point_t – The external spacepoint type.
Public Types
-
using value_type = TripletCandidate<external_space_point_t>
Public Functions
-
CandidatesForMiddleSp() = default
constructor
-
~CandidatesForMiddleSp() = default
Destructor.
-
void clear()
Clear the internal storage.
-
bool push(external_space_point_t &SpB, external_space_point_t &SpM, external_space_point_t &SpT, float weight, float zOrigin, bool isQuality)
Adding a new triplet candidate to the collection, should it satisfy the selection criteria.
- Parameters
SpB – Bottom space point
SpM – Medium space point
SpT – Top space point
weight – The quality of the triplet candidate
zOrigin – The z-coordinate of the origin
isQuality – Whether the triplet candidate is high or low quality
- Returns
whether the triplet candidate has been added or not to the collection
-
void setMaxElements(std::size_t n_low, std::size_t n_high)
Setting maximum number of candidates to keep.
- Parameters
n_low – Maximum number of candidates in the low-quality collection
n_high – Maximum number of candidates in the high-quality collection
-
std::vector<value_type> storage()
Retrieve the triplet candidates, the resulting vector is already sorted, elements with higher quality first.
- Returns
Vector of triplet candidates
Public Static Functions
-
static bool ascendingByQuality(const value_type &i1, const value_type &i2)
A function for sorting the triplet candidates from lower to higher quality.
- Parameters
i1 – First triplet candidate
i2 – Second triplet candidate
- Returns
The comparison result
-
static bool descendingByQuality(const value_type &i1, const value_type &i2)
A function for sorting the triplet candidates from higher to lower quality.
- Parameters
i1 – First triplet candidate
i2 – Second triplet candidate
- Returns
The comparison result
-
class CartesianSegmentation : public Acts::Segmentation
- #include <Acts/Digitization/CartesianSegmentation.hpp>
Segmentation Base class.
Segmentation class for generic pixel, strixels and strip segmentations in a cartesian frame, this uses a cartesian X/Y local surface definition
The calculation can be done in full 3D, i.e. the segments of the path through the planar module are calculated in a 3D model - or in 2D, when the entire calculation is done on the projective surface. When the 2D option is used, segmentation surfaces are not created. The 2D calculation is faster and uses less memory, however, effects within the sensor volume can not be easily integrated
Conventions:
3D positions are within the 3D frame of the module
2D positions are corrected to the readout surface they need to be corrected by the lorentzShift for the parameter surface in the center of the surface)
Public Functions
Constructor for all same-size pixels or strips (in cas numCellsY is set to 1)
- Parameters
mBounds – are the rectangle bounds of the sensitive volume
numCellsX – is the number of cells in X
numCellsY – is the number of cells in Y
Note
if both RectangleBounds and BinUtility are provided, no check is done for consistency
- Parameters
bUtility – is the bin Utility,
mBounds – are the rectangle bounds if provided for memory optimisation
-
~CartesianSegmentation() override
Virtual Destructor.
-
inline virtual const BinUtility &binUtility() const final
return the bin utility that defines the readout segmentation
-
inline virtual DigitizationCell cell(const Vector2 &position) const final
Get the digitization cell from a 3D position.
ignores the shift, i.e. assumenes in to be in cell frame
- Parameters
position – is the position for which the cell is requested
- Returns
is a cell with cell ids
-
inline virtual DigitizationCell cell(const Vector3 &position) const final
Get the digitization cell from a 3D position.
ignores the shift, i.e. assumenes in to be in cell frame
- Parameters
position – is the position for which the cell is requested
- Returns
is a cell with cell ids
-
virtual Vector2 cellPosition(const DigitizationCell &dCell) const final
Calculate the cell Position from the Id.
- Parameters
dCell – the digitization cell
- Returns
the center position of the associated cell
-
virtual void createSegmentationSurfaces(SurfacePtrVector &boundarySurfaces, SurfacePtrVector &segmentationSurfacesX, SurfacePtrVector &segmentationSurfacesY, double halfThickness, int readoutDirection = 1., double lorentzAngle = 0.) const final
Create the segmentation surfaces in X.
This method is only used if the full 3D digitization is done
Create the segmentation surfaces in X and Y for rectangular shapes These are needed for a full three dimensional module
- Parameters
boundarySurfaces – vector to be filled
segmentationSurfacesX – are the segmetation boundaries in X
segmentationSurfacesY – are the segmetation boundaries in Y
halfThickness – is the half thickness in z of the module
readoutDirection – is the direction w.r.t normal vector where the readout is given : -1, 0, 1 possible
lorentzAngle – is the lorentz angle measured from the local z towards x axis
-
virtual DigitizationStep digitizationStep(const Vector3 &start, const Vector3 &end, double halfThickness, int readoutDirection = 1, double lorentzAngle = 0.) const final
Fill the associated digitization cell from this start and end position correct for lorentz effect if needed.
Fill the associated digitization cell from the start and end position in 3D correct for lorentz effect if needed.
- Parameters
start – is the start position of the step
end – is the end position of the step
halfThickness – is the half thickness in z
readoutDirection – is the readout direction with respect to local z
lorentzAngle – is the lorentz angle measured from local z towards x
- Returns
is a fully calculated digitzation step
-
inline virtual const PlanarBounds &moduleBounds() const final
return the surface bounds by reference specialization for Rectangle Bounds
-
inline std::pair<double, double> pitch() const
return the pitch sizes as a pair
-
template<typename propagator_t, typename traj_t>
class CombinatorialKalmanFilter - #include <Acts/TrackFinding/CombinatorialKalmanFilter.hpp>
Combinatorial Kalman filter to find tracks.
The CombinatorialKalmanFilter contains an Actor and a Sequencer sub-class. The Sequencer has to be part of the Navigator of the Propagator in order to initialize and provide the measurement surfaces.
The Actor is part of the Propagation call and does the Kalman update and eventually the smoothing. Updater, Smoother and Calibrator are given to the Actor for further use:
The Updater is the implemented kalman updater formalism, it runs via a visitor pattern through the measurements.
The Smoother is called at the end of the filtering (track finding) by the Actor.
Measurements are not required to be ordered for the CombinatorialKalmanFilter, measurement ordering needs to be figured out by the navigation of the propagator.
The void components are provided mainly for unit testing.
- Template Parameters
propagator_t – Type of the propagator
Public Functions
-
CombinatorialKalmanFilter() = delete
Default constructor is deleted.
-
inline CombinatorialKalmanFilter(propagator_t pPropagator, std::unique_ptr<const Logger> _logger = getDefaultLogger("CKF", Logging::INFO))
Constructor from arguments.
-
template<typename source_link_iterator_t, typename start_parameters_t, typename track_container_t, template<typename> class holder_t, typename parameters_t = BoundTrackParameters>
inline auto findTracks(const start_parameters_t &initialParameters, const CombinatorialKalmanFilterOptions<source_link_iterator_t, traj_t> &tfOptions, TrackContainer<track_container_t, traj_t, holder_t> &trackContainer) const -> Result<std::vector<typename std::decay_t<decltype(trackContainer)>::TrackProxy>> Combinatorial Kalman Filter implementation, calls the Kalman filter and smoother.
Note
The input measurements are given in the form of
SourceLinks. It’scalibrator_t'sjob to turn them into calibrated measurements used in the track finding.- Template Parameters
source_link_iterator_t – Type of the source link iterator
start_parameters_container_t – Type of the initial parameters container
calibrator_t – Type of the source link calibrator
measurement_selector_t – Type of the measurement selector
track_container_t – Type of the track container backend
holder_t – Type defining track container backend ownership
parameters_t – Type of parameters used for local parameters
- Parameters
initialParameters – The initial track parameters
tfOptions – CombinatorialKalmanFilterOptions steering the track finding
trackContainer – Input track container to use
- Returns
a container of track finding result for all the initial track parameters
-
template<typename traj_t>
struct CombinatorialKalmanFilterExtensions - #include <Acts/TrackFinding/CombinatorialKalmanFilter.hpp>
Extension struct which holds the delegates to customize the CKF behavior.
Public Types
-
using BranchStopper = Delegate<bool(const CombinatorialKalmanFilterTipState&)>
-
using candidate_container_t = typename std::vector<typename traj_t::TrackStateProxy>
-
using MeasurementSelector = Delegate<Result<std::pair<typename candidate_container_t::iterator, typename candidate_container_t::iterator>>(candidate_container_t &trackStates, bool&, const Logger&)>
Public Functions
-
inline CombinatorialKalmanFilterExtensions()
Default constructor which connects the default void components.
Public Members
-
BranchStopper branchStopper
-
KalmanFitterExtensions<traj_t>::Calibrator calibrator
The Calibrator is a dedicated calibration algorithm that allows to calibrate measurements using track information, this could be e.g.
sagging for wires, module deformations, etc.
-
MeasurementSelector measurementSelector
The measurement selector is called during the filtering by the Actor.
-
KalmanFitterExtensions<traj_t>::Smoother smoother
The smoother back-propagates measurement information along the track.
-
KalmanFitterExtensions<traj_t>::Updater updater
The updater incorporates measurement information into the track parameters.
-
using BranchStopper = Delegate<bool(const CombinatorialKalmanFilterTipState&)>
-
template<typename source_link_iterator_t, typename traj_t>
struct CombinatorialKalmanFilterOptions - #include <Acts/TrackFinding/CombinatorialKalmanFilter.hpp>
Combined options for the combinatorial Kalman filter.
- Template Parameters
source_link_accessor_t – Source link accessor type, should be semiregular.
Public Types
-
using SourceLinkAccessor = SourceLinkAccessorDelegate<source_link_iterator_t>
-
using SourceLinkIterator = source_link_iterator_t
Public Functions
-
CombinatorialKalmanFilterOptions() = delete
Contexts are required and the options must not be default-constructible.
-
inline CombinatorialKalmanFilterOptions(const GeometryContext &gctx, const MagneticFieldContext &mctx, std::reference_wrapper<const CalibrationContext> cctx, SourceLinkAccessor accessor_, CombinatorialKalmanFilterExtensions<traj_t> extensions_, const PropagatorPlainOptions &pOptions, const Surface *rSurface = nullptr, bool mScattering = true, bool eLoss = true, bool rSmoothing = true)
PropagatorOptions with context.
- Parameters
gctx – The geometry context for this track finding/fitting
mctx – The magnetic context for this track finding/fitting
cctx – The calibration context for this track finding/fitting
accessor_ – The source link accessor
extensions_ – The extension struct
pOptions – The plain propagator options
rSurface – The reference surface for the eventual track fitting to be expressed at
mScattering – Whether to include multiple scattering
eLoss – Whether to include energy loss
rSmoothing – Whether to run smoothing to get fitted parameter
Public Members
-
std::reference_wrapper<const CalibrationContext> calibrationContext
context object for the calibration
-
bool energyLoss = true
Whether to consider energy loss.
-
CombinatorialKalmanFilterExtensions<traj_t> extensions
The filter extensions.
-
const Surface *filterTargetSurface = nullptr
The filter target surface.
-
std::reference_wrapper<const GeometryContext> geoContext
Context object for the geometry.
-
std::reference_wrapper<const MagneticFieldContext> magFieldContext
Context object for the magnetic field.
-
bool multipleScattering = true
Whether to consider multiple scattering.
-
PropagatorPlainOptions propagatorPlainOptions
The trivial propagator options.
-
bool smoothing = true
Whether to run smoothing to get fitted parameter.
-
const Surface *smoothingTargetSurface = nullptr
The smoothing target surface.
-
SourceLinkAccessor sourcelinkAccessor
The source link accessor.
-
template<typename traj_t>
struct CombinatorialKalmanFilterResult - #include <Acts/TrackFinding/CombinatorialKalmanFilter.hpp>
Public Members
-
AbortList<PathLimitReached, EndOfWorldReached> abortList
-
std::vector<std::pair<MultiTrajectoryTraits::IndexType, CombinatorialKalmanFilterTipState>> activeTips
-
bool filtered = false
-
bool finished = false
-
std::unordered_map<MultiTrajectoryTraits::IndexType, BoundTrackParameters> fittedParameters
-
traj_t *fittedStates = {nullptr}
-
MultiTrajectoryTraits::IndexType iSmoothed = 0
-
std::vector<MultiTrajectoryTraits::IndexType> lastMeasurementIndices
-
std::vector<MultiTrajectoryTraits::IndexType> lastTrackIndices
-
bool smoothed = false
-
std::unordered_map<const Surface*, std::unordered_map<size_t, size_t>> sourcelinkTips
-
std::shared_ptr<traj_t> stateBuffer
-
std::vector<typename traj_t::TrackStateProxy> trackStateCandidates
-
AbortList<PathLimitReached, EndOfWorldReached> abortList
-
struct CombinatorialKalmanFilterTipState
- #include <Acts/TrackFinding/CombinatorialKalmanFilter.hpp>
Track quality summary for one trajectory.
This could be used to decide if a track is to be recorded when the filtering is done or to be terminated due to its bad quality
Public Members
-
size_t nHoles = 0
-
size_t nMeasurements = 0
-
size_t nOutliers = 0
-
size_t nSensitiveSurfaces = 0
-
size_t nStates = 0
-
size_t nHoles = 0
-
class ConeBounds : public Acts::SurfaceBounds
- #include <Acts/Surfaces/ConeBounds.hpp>
Bounds for a conical surface, the opening angle is stored in \( \tan(\alpha) \) and always positively defined.
The cone can open to both sides, steered by \( z_min \) and \( z_max \).
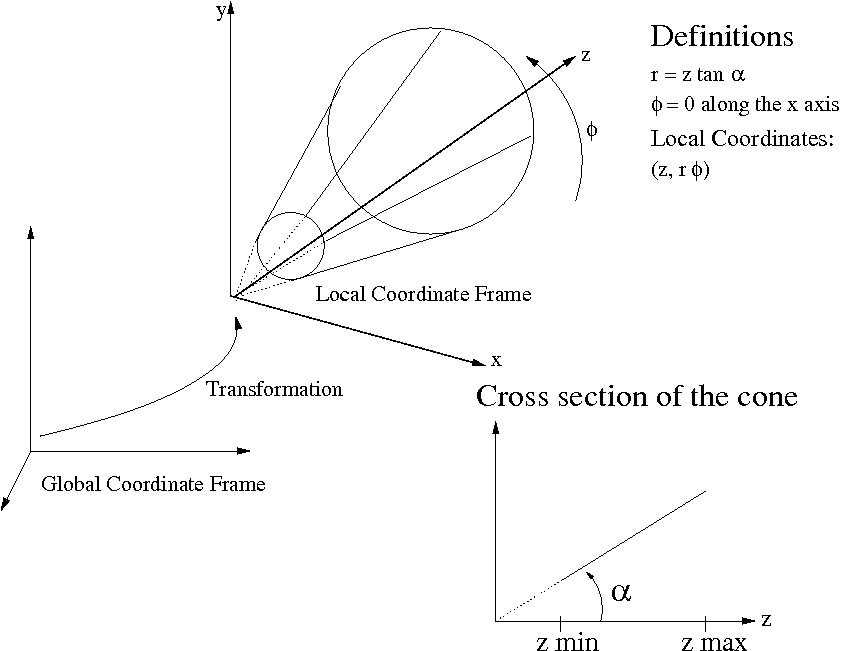
Public Types
-
enum BoundValues
Values:
-
enumerator eAlpha
-
enumerator eMinZ
-
enumerator eMaxZ
-
enumerator eHalfPhiSector
-
enumerator eAveragePhi
-
enumerator eSize
-
enumerator eAlpha
Public Functions
-
ConeBounds() = delete
-
ConeBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor - from parameters array.
- Parameters
values – The parameter array
-
ConeBounds(double alpha, bool symm, double halfphi = M_PI, double avphi = 0.) noexcept(false)
Constructor - open cone with alpha, by default a full cone but optionally can make a conical section.
- Parameters
alpha – is the opening angle of the cone
symm – is the boolean indicating if the cone is symmetric in +/- z
halfphi – is the half opening angle (default is pi)
avphi – is the phi value around which the bounds are opened (default=0)
-
ConeBounds(double alpha, double minz, double maxz, double halfphi = M_PI, double avphi = 0.) noexcept(false)
Constructor - open cone with alpha, minz and maxz, by default a full cone but can optionally make it a conical section.
- Parameters
alpha – is the opening angle of the cone
minz – cone expanding from minimal z
maxz – cone expanding to maximal z
halfphi – is the half opening angle (default is pi)
avphi – is the phi value around which the bounds are opened (default=0)
-
~ConeBounds() override = default
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck = true) const final
inside method for local position
- Parameters
lposition – is the local position to be checked
bcheck – is the boundary check directive
- Returns
is a boolean indicating if the position is inside
-
inline double r(double z) const
Return the radius at a specific z values.
- Parameters
z – is the z value for which r is requested
- Returns
is the r value associated with z
-
inline double tanAlpha() const
Return tangent of alpha (pre-computed)
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
- Parameters
sl – is the ostrea into which the dump is done
- Returns
is the input object
-
virtual BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
enum BoundValues
-
class ConeLayer : public virtual Acts::ConeSurface, public Acts::Layer
- #include <Acts/Geometry/ConeLayer.hpp>
Class to describe a conical detector layer for tracking, it inhertis from both, Layer base class and ConeSurface class.
Public Functions
-
ConeLayer() = delete
-
ConeLayer(const ConeLayer &cla) = delete
-
~ConeLayer() override = default
-
virtual const ConeSurface &surfaceRepresentation() const override
Transforms the layer into a Surface representation for extrapolation.
-
virtual ConeSurface &surfaceRepresentation() override
Public Static Functions
Factory for shared layer.
- Parameters
transform – is the 3D transform that positions the layer in 3D frame
cbounds – is the conical bound description
surfaceArray – is the array of sensitive surfaces
thickness – is the layer thickness along the normal axis
ad – is the approach descriptor for navigation towards the layer
laytyp – is the layer type
- Returns
is a shared pointer to a layer
-
ConeLayer() = delete
-
class ConeSurface : public Acts::Surface
- #include <Acts/Surfaces/ConeSurface.hpp>
Class for a conical surface in the Tracking geometry.
It inherits from Surface.
The ConeSurface is special since no corresponding Track parameters exist since they’re numerical instable at the tip of the cone. Propagations to a cone surface will be returned in curvilinear coordinates.
Subclassed by Acts::ConeLayer
Public Functions
-
ConeSurface() = delete
-
~ConeSurface() override = default
-
virtual AlignmentToPathMatrix alignmentToPathDerivative(const GeometryContext &gctx, const FreeVector ¶meters) const final
Calculate the derivative of path length at the geometry constraint or point-of-closest-approach w.r.t.
alignment parameters of the surface (i.e. local frame origin in global 3D Cartesian coordinates and its rotation represented with extrinsic Euler angles)
- Parameters
gctx – The current geometry context object, e.g. alignment
parameters – is the free parameters
- Returns
Derivative of path length w.r.t. the alignment parameters
-
virtual Vector3 binningPosition(const GeometryContext &gctx, BinningValue bValue) const final
The binning position method - is overloaded for r-type binning.
- Parameters
gctx – The current geometry context object, e.g. alignment
bValue – defines the type of binning applied in the global frame
- Returns
The return type is a vector for positioning in the global frame
-
virtual const ConeBounds &bounds() const final
This method returns the ConeBounds by reference.
-
virtual Result<Vector2> globalToLocal(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, double tolerance = s_onSurfaceTolerance) const final
Global to local transformation.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the global position to be transformed
direction – is the global momentum direction (ignored in this operation)
tolerance – optional tolerance within which a point is considered valid on surface
- Returns
a Result<Vector2> which can be !ok() if the operation fails
-
virtual SurfaceIntersection intersect(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck = false, double tolerance = s_onSurfaceTolerance) const final
Straight line intersection schema from position/direction.
If possible returns both solutions for the cylinder
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The position to start from
direction – The direction at start
bcheck – the Boundary Check
tolerance – the tolerance used for the intersection
- Returns
SurfaceIntersection object (contains intersection & surface)
-
virtual ActsMatrix<2, 3> localCartesianToBoundLocalDerivative(const GeometryContext &gctx, const Vector3 &position) const final
Calculate the derivative of bound track parameters local position w.r.t.
position in local 3D Cartesian coordinates
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The position of the parameters in global
- Returns
Derivative of bound local position w.r.t. position in local 3D cartesian coordinates
-
virtual Vector3 localToGlobal(const GeometryContext &gctx, const Vector2 &lposition, const Vector3 &direction) const final
Local to global transformation.
- Parameters
gctx – The current geometry context object, e.g. alignment
lposition – is the local position to be transformed
direction – is the global momentum direction (ignored in this operation)
- Returns
The global position by value
-
virtual std::string name() const override
Return properly formatted class name for screen output.
-
inline Vector3 normal(const GeometryContext &gctx) const
Normal vector return without argument.
-
virtual Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const final
Return method for surface normal information.
- Parameters
gctx – The current geometry context object, e.g. alignment
lposition – is the local position at normal vector request
- Returns
Vector3 normal vector in global frame
-
Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const = 0
Normal vector return without argument.
-
Vector3 normal(const GeometryContext &gctx, const Vector3 &position) const
Normal vector return without argument.
-
virtual Vector3 normal(const GeometryContext &gctx, const Vector3 &position) const final
Return method for surface normal information.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the global position as normal vector base
- Returns
Vector3 normal vector in global frame
-
ConeSurface &operator=(const ConeSurface &other)
Assignment operator.
- Parameters
other – is the source surface for the assignment
-
virtual double pathCorrection(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const final
The pathCorrection for derived classes with thickness.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the global potion at the correction point
direction – is the momentum direction at the correction point
- Returns
is the path correction due to incident angle
-
virtual Polyhedron polyhedronRepresentation(const GeometryContext &gctx, size_t lseg) const override
Return a Polyhedron for the surfaces.
Note
that a surface transform can invalidate the extrema in the transformed space
- Parameters
gctx – The current geometry context object, e.g. alignment
lseg – Number of segments along curved lines, it represents the full 2*M_PI coverange, if lseg is set to 1 only the extrema are given
- Returns
A list of vertices and a face/facett description of it
-
virtual RotationMatrix3 referenceFrame(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const final
Return the measurement frame - this is needed for alignment, in particular for StraightLine and Perigee Surface.
the default implementation is the RotationMatrix3 of the transform
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the global position where the measurement frame is constructed
direction – is the momentum direction used for the measurement frame construction
- Returns
matrix that indicates the measurement frame
-
virtual Vector3 rotSymmetryAxis(const GeometryContext &gctx) const
- Parameters
gctx – The current geometry context object, e.g. alignment
-
virtual SurfaceType type() const override
Return the surface type.
-
ConeSurface() = delete
-
class ConeVolumeBounds : public Acts::VolumeBounds
- #include <Acts/Geometry/ConeVolumeBounds.hpp>
Volume bound class for describing conical volumes either with cylindrical inlay or outer boundary, it also allows for a sectoral description.
Public Types
-
enum BoundValues
for readability
Values:
-
enumerator eInnerAlpha
-
enumerator eInnerOffsetZ
-
enumerator eOuterAlpha
-
enumerator eOuterOffsetZ
-
enumerator eHalfLengthZ
-
enumerator eAveragePhi
-
enumerator eHalfPhiSector
-
enumerator eSize
-
enumerator eInnerAlpha
Public Functions
-
ConeVolumeBounds() = delete
-
ConeVolumeBounds(const ConeVolumeBounds &cobo) = default
-
inline ConeVolumeBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor - from a fixed size array.
- Parameters
values – The bound values
-
ConeVolumeBounds(double cylinderR, double alpha, double offsetZ, double halflengthZ, double averagePhi, double halfPhiSector) noexcept(false)
Constructor - for general cylidner-cone setups.
Note
depending on cylinderR > coneR it is constructing a cone with cylindrical cutout or a cylinder with conical cutout
- Parameters
cylinderR – The inner radius of the cylinder
alpha – The opening angle of the cone (0 if no cone)
offsetZ – The tip z position in of the cone, w.r.t center
halflengthZ – The minimum z value of the inner and outer cones
averagePhi – The phi orientation of the sector (defaulted to 0)
halfPhiSector – The opening angle phi sector
-
ConeVolumeBounds(double innerAlpha, double innerOffsetZ, double outerAlpha, double outerOffsetZ, double halflengthZ, double averagePhi, double halfPhiSector) noexcept(false)
Constructor - for general cone-cone setups.
- Parameters
innerAlpha – The opening angle of the inner cone (0 if no cone)
innerOffsetZ – The tip z position in of the inner cone, w.r.t center
outerAlpha – The opening angle of the outer cone (0 if no cone)
outerOffsetZ – The tip z position in of the outer cone, w.r.t center
halflengthZ – The minimum z value of the inner and outer cones
averagePhi – The phi orientation of the sector
halfPhiSector – The opening angle phi sector
-
~ConeVolumeBounds() override = default
-
virtual Volume::BoundingBox boundingBox(const Transform3 *trf = nullptr, const Vector3 &envelope = {0, 0, 0}, const Volume *entity = nullptr) const final
Construct bounding box for this shape.
- Parameters
trf – Optional transform
envelope – Optional envelope to add / subtract from min/max
entity – Entity to associate this bounding box with
- Returns
Constructed bounding box
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
inline double innerRmax() const
-
inline double innerRmin() const
-
inline double innerTanAlpha() const
-
virtual bool inside(const Vector3 &pos, double tol = 0.) const final
This method checks if position in the 3D volume frame is inside the cylinder.
- Parameters
pos – is the position in volume frame to be checked
tol – is the absolute tolerance to be applied
-
ConeVolumeBounds &operator=(const ConeVolumeBounds &cobo) = default
-
virtual OrientedSurfaces orientedSurfaces(const Transform3 &transform = Transform3::Identity()) const final
Oriented surfaces, i.e.
the decomposed boundary surfaces and the according navigation direction into the volume given the normal vector on the surface
It will throw an exception if the orientation prescription is not adequate
- Parameters
transform – is the 3D transform to be applied to the boundary surfaces to position them in 3D space
- Returns
a vector of surfaces bounding this volume
-
inline double outerRmax() const
-
inline double outerRmin() const
-
inline double outerTanAlpha() const
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
- Parameters
sl – is ostream operator to be dumped into
-
inline virtual VolumeBounds::BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
enum BoundValues
-
class ConstantBField : public Acts::MagneticFieldProvider
- #include <Acts/MagneticField/ConstantBField.hpp>
This class implements a simple constant magnetic field.
The magnetic field value has to be set at creation time, but can be updated later on.
Public Functions
-
inline explicit ConstantBField(Vector3 B)
Construct constant magnetic field from field vector.
- Parameters
B – [in] magnetic field vector in global coordinate system
-
inline Vector3 getField() const
Get the B field at a position.
-
inline virtual Result<Vector3> getField(const Vector3 &position, MagneticFieldProvider::Cache &cache) const override
Retrieve magnetic field value at a given location.
Requires a cache object created through makeCache().
Note
The
positionis ignored and only kept as argument to provide a consistent interface with other magnetic field services.- Parameters
position – [in] global 3D position for the lookup
cache – [inout] Field provider specific cache object
- Returns
magnetic field vector at given position
-
inline virtual Result<Vector3> getFieldGradient(const Vector3 &position, ActsMatrix<3, 3> &derivative, MagneticFieldProvider::Cache &cache) const override
Retrieve magnetic field value its its gradient.
Requires a cache object created through makeCache().
Note
The
positionis ignored and only kept as argument to provide a consistent interface with other magnetic field services.Note
currently the derivative is not calculated
- Parameters
position – [in] global 3D position
derivative – [out] gradient of magnetic field vector as (3x3) matrix
cache – [inout] Field provider specific cache object
- Returns
magnetic field vector
-
inline bool isInside(const Vector3 &position) const
check whether given 3D position is inside look-up domain
- Parameters
position – [in] global 3D position
- Returns
Always true for constant magnetic field
-
inline virtual Acts::MagneticFieldProvider::Cache makeCache(const Acts::MagneticFieldContext &mctx) const override
Make an opaque cache for the magnetic field.
Instructs the specific implementation to generate a
Cacheinstance for magnetic field lookup.- Parameters
mctx – The magnetic field context to generate cache for
- Returns
Cache The opaque cache object
-
inline void setField(const Vector3 &B)
update magnetic field vector
- Parameters
B – [in] magnetic field vector in global coordinate system
-
struct Cache
- #include <Acts/MagneticField/ConstantBField.hpp>
Public Functions
-
inline Cache(const MagneticFieldContext&)
constructor with context
-
inline Cache(const MagneticFieldContext&)
-
inline explicit ConstantBField(Vector3 B)
-
class ConstrainedStep
- #include <Acts/Propagator/ConstrainedStep.hpp>
A constrained step class for the steppers.
This class is symmetrical for forward and backward propagation. The sign of the propagation direction should not enter here but rather be applied the step is actually taken.
As simple as this class looks it hides a few very important details:
Overstepping handling. The step size sign will flip if we happened to pass our target.
Convergence handling. Smaller and smaller step sizes have to be used in order to converge on a target.
Because of the points mentioned above, the update function will always prefer negative step sizes. A side effect of this is that we will propagate in the opposite direction if the target is “behind us”.
The hierarchy is:
Overstepping resolution / backpropagation
Convergence
Step into the void with
std::numeric_limits<Scalar>max()
Public Types
-
using Scalar = ActsScalar
-
enum Type
the types of constraints from accuracy - this can vary up and down given a good step estimator from actor - this would be a typical navigation step from aborter - this would be a target condition from user - this is user given for what reason ever
Values:
-
enumerator accuracy
-
enumerator actor
-
enumerator aborter
-
enumerator user
-
enumerator accuracy
Public Functions
-
constexpr ConstrainedStep() = default
-
inline explicit constexpr ConstrainedStep(Scalar value)
constructor from Scalar
- Parameters
value – is the user given initial value
-
inline constexpr Type currentType() const
Access the currently leading type.
-
inline constexpr void release(Type type)
release a certain constraint value
- Parameters
type – is the constraint type to be released
-
inline constexpr void scale(Scalar factor)
-
inline constexpr void setValue(Scalar value)
set accuracy by one Scalar
this will set only the accuracy, as this is the most exposed to the Propagator
- Parameters
value – is the new accuracy value
-
inline std::ostream &toStream(std::ostream &os) const
-
inline std::string toString() const
-
inline constexpr void update(Scalar value, Type type, bool releaseStep = false)
Update the step size of a certain type.
Only navigation and target abortion step size updates may change the sign due to overstepping
- Parameters
value – is the new value to be updated
type – is the constraint type
releaseStep – Allow step size to increase again
-
inline constexpr Scalar value() const
returns the min step size
Public Members
-
size_t nStepTrials = std::numeric_limits<size_t>::max()
Number of iterations needed by the stepsize finder (e.g.
Runge-Kutta) of the stepper.
-
class ConstTrackStateType
- #include <Acts/EventData/TrackStateType.hpp>
View type over a bitset stored in a 64 bit integer This view does not allow modifications.
Public Types
-
using raw_type = std::uint64_t
Public Functions
-
inline ConstTrackStateType(const raw_type &raw)
Constructor from a reference to the underlying value container.
- Parameters
raw – the value container
-
inline bool test(std::size_t pos) const
Return if the bit at position
posis 1.- Parameters
pos – the bit position
- Returns
if the bit at
posis one or not
Public Static Attributes
-
static constexpr std::size_t kRawBits = std::numeric_limits<std::make_unsigned<raw_type>::type>::digits
Friends
-
inline friend std::ostream &operator<<(std::ostream &os, ConstTrackStateType t)
-
using raw_type = std::uint64_t
-
class ConstVectorMultiTrajectory : public Acts::detail_vmt::VectorMultiTrajectoryBase, public Acts::MultiTrajectory<ConstVectorMultiTrajectory>
- #include <Acts/EventData/VectorMultiTrajectory.hpp>
Public Functions
-
ConstVectorMultiTrajectory() = default
-
inline ConstVectorMultiTrajectory(const ConstVectorMultiTrajectory &other)
-
inline ConstVectorMultiTrajectory(const VectorMultiTrajectory &other)
-
ConstVectorMultiTrajectory(ConstVectorMultiTrajectory&&) = default
-
inline ConstVectorMultiTrajectory(VectorMultiTrajectory &&other)
-
inline std::any component_impl(HashedString key, IndexType istate) const
-
inline ConstTrackStateProxy::Covariance covariance_impl(IndexType parIdx) const
-
inline constexpr bool has_impl(HashedString key, IndexType istate) const
-
inline constexpr bool hasColumn_impl(HashedString key) const
-
inline ConstTrackStateProxy::Covariance jacobian_impl(IndexType istate) const
-
template<size_t measdim>
inline ConstTrackStateProxy::Measurement<measdim> measurement_impl(IndexType istate) const
-
template<size_t measdim>
inline ConstTrackStateProxy::MeasurementCovariance<measdim> measurementCovariance_impl(IndexType istate) const
-
inline ConstTrackStateProxy::Parameters parameters_impl(IndexType parIdx) const
-
inline IndexType size_impl() const
-
inline Statistics statistics() const
-
ConstVectorMultiTrajectory() = default
-
class ConstVectorTrackContainer : public Acts::detail_vtc::VectorTrackContainerBase
- #include <Acts/EventData/VectorTrackContainer.hpp>
Public Functions
-
inline ConstVectorTrackContainer()
-
ConstVectorTrackContainer(const ConstVectorTrackContainer &other) = default
-
inline ConstVectorTrackContainer(const VectorTrackContainer &other)
-
ConstVectorTrackContainer(ConstVectorTrackContainer&&) = default
-
inline ConstVectorTrackContainer(VectorTrackContainer &&other)
-
inline std::any component_impl(HashedString key, IndexType itrack) const
-
inline ConstCovariance covariance(IndexType itrack) const
-
inline ConstParameters parameters(IndexType itrack) const
-
inline ConstVectorTrackContainer()
-
template<int N>
class ConvexPolygonBounds : public Acts::ConvexPolygonBoundsBase - #include <Acts/Surfaces/ConvexPolygonBounds.hpp>
This is the actual implementation of the bounds.
It is templated on the number of vertices, but there is a specialization for dynamic number of vertices, where the underlying storage is then a vector.
- Template Parameters
N – Number of vertices
Public Types
-
using value_array = std::array<double, eSize>
Type that’s used to store the vertices, in this case a fixed size array.
-
using vertex_array = std::array<Vector2, num_vertices>
Type that’s used to store the vertices, in this case a fixed size array.
Public Functions
-
ConvexPolygonBounds() = delete
-
ConvexPolygonBounds(const std::vector<Vector2> &vertices) noexcept(false)
Constructor from a vector of vertices, to facilitate construction.
This will throw if the vector size does not match
num_vertices. This will throw if the vertices do not form a convex polygon.- Parameters
vertices – The list of vertices.
-
ConvexPolygonBounds(const value_array &values) noexcept(false)
Constructor from a fixed size array of parameters This will throw if the vertices do not form a convex polygon.
- Parameters
values – The values to build up the vertices
-
ConvexPolygonBounds(const vertex_array &vertices) noexcept(false)
Constructor from a fixed size array of vertices.
This will throw if the vertices do not form a convex polygon.
- Parameters
vertices – The vertices
-
~ConvexPolygonBounds() override = default
-
virtual const RectangleBounds &boundingBox() const final
Return a rectangle bounds object that encloses this polygon.
- Returns
The rectangular bounds
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck) const final
Return whether a local 2D point lies inside of the bounds defined by this object.
- Parameters
lposition – The local position to check
bcheck – The
BoundaryCheckobject handling tolerances.
- Returns
Whether the points is inside
-
virtual BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
virtual std::vector<Vector2> vertices(unsigned int lseg = 1) const final
Return the vertices.
Note
the number of segments is ignored in this representation
- Parameters
lseg – the number of segments used to approximate and eventually curved line
- Returns
vector for vertices in 2D
-
template<>
class ConvexPolygonBounds<PolygonDynamic> : public Acts::ConvexPolygonBoundsBase - #include <Acts/Surfaces/ConvexPolygonBounds.hpp>
This is the specialization handling a polygon with a dynamic number of points.
It can accept any number of points.
Public Functions
-
ConvexPolygonBounds() = delete
Default constructor, deleted.
-
ConvexPolygonBounds(const std::vector<Vector2> &vertices)
Constructor from a vector of vertices, to facilitate construction.
This will throw if the vertices do not form a convex polygon.
- Parameters
vertices – The list of vertices.
-
~ConvexPolygonBounds() override = default
Defaulted destructor.
-
virtual const RectangleBounds &boundingBox() const final
Return a rectangle bounds object that encloses this polygon.
- Returns
The rectangular bounds
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck) const final
Return whether a local 2D point lies inside of the bounds defined by this object.
- Parameters
lposition – The local position to check
bcheck – The
BoundaryCheckobject handling tolerances.
- Returns
Whether the points is inside
-
virtual BoundsType type() const final
Return the bounds type of this bounds object.
- Returns
The bounds type
-
virtual std::vector<Vector2> vertices(unsigned int lseg = 1) const final
Return the vertices.
Note
the number of segments is ignored in this representation
- Parameters
lseg – the number of segments used to approximate and eventually curved line
- Returns
vector for vertices in 2D
-
ConvexPolygonBounds() = delete
-
class ConvexPolygonBoundsBase : public Acts::PlanarBounds
- #include <Acts/Surfaces/ConvexPolygonBounds.hpp>
base class for convex polygon bounds
This class serves as a base class for the actual bounds class. The only deriving type is the templated
ConvexPolygonBounds.Subclassed by Acts::ConvexPolygonBounds< N >, Acts::ConvexPolygonBounds< PolygonDynamic >
Public Functions
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
- Parameters
sl – is the ostream to be written into
-
virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
virtual std::ostream &toStream(std::ostream &sl) const final
-
struct CovarianceCache
- #include <Acts/Propagator/CovarianceTransport.hpp>
Helper struct holding the necessary cache for the Covariance transport in various parametrisations.
Public Functions
-
CovarianceCache() = default
Defaulted constructor, gives invalid cache.
-
CovarianceCache(const FreeVector &freeParameters, const FreeSquareMatrix &freeCovariance)
Construction from free.
- Parameters
freeParameters – The free parameters
freeCovariance – The free covariance to be propagated
-
CovarianceCache(const GeometryContext &gctx, const Surface &surface, const Vector3 &position, const BoundVector &boundParameters, const BoundSquareMatrix &boundCovariance)
Constructor from bound & surface.
This constructor will set the variant covariance type to a bound matrix, remember the surface & establish the jacobian between bound and free parametrisation.
- Parameters
gctx – The current geometry context
surface – The surface of the bound representation
position – The position of the representation
boundParameters – The bound parameters at the surface
boundCovariance – The bound covariance to be propagated
-
CovarianceCache(const Vector3 &position, const Vector3 &direction, const BoundSquareMatrix &boundCovariance)
Constructor from curvilinear.
This constructor will set the variant covariance type to a bound matrix, remember the surface & establish the jacobian between bound and free parametrisation.
- Parameters
position – The position of the representation
direction – The direction of at the representation
boundCovariance – The bound covariance to be propagated
Public Members
-
std::optional<ActsMatrix<8, 7>> anglesToDirectionJacobian = std::nullopt
Options for starting from free.
-
bool applyTransport = false
Internal cache state, indicates correct setup.
-
const Surface *atSurface = nullptr
Internal cache state, at surface indication.
-
std::optional<BoundToFreeMatrix> boundToFreeJacobian = std::nullopt
Optional for starting from bound or curvilinear.
-
VariantCovariance covariance
Variant: the currently held covariance.
-
std::optional<ActsMatrix<7, 8>> directionToAnglesJacobian = std::nullopt
-
FreeVector freeToPathDerivatives = FreeVector::Zero()
Non-variant: the free derivatives.
-
FreeMatrix freeTransportJacobian = FreeMatrix::Identity()
Non-variant: the free transport jacobian.
-
CovarianceCache() = default
-
class CuboidVolumeBounds : public Acts::VolumeBounds
- #include <Acts/Geometry/CuboidVolumeBounds.hpp>
Bounds for a cubical Volume, the orientedSurfaces(…) method creates a vector of 6 surfaces:
BoundarySurfaceFace [index]:
negativeFaceXY [0] : Rectangular Acts::PlaneSurface, parallel to \( xy \) plane at negative \( z \)
positiveFaceXY [1] : Rectangular Acts::PlaneSurface, parallel to \( xy \) plane at positive \( z \)
negativeFaceXY [2] : Rectangular Acts::PlaneSurface, attached to \( yz \) plane at negative \( x \)
positiveFaceXY [3] : Rectangular Acts::PlaneSurface, attached to \( yz \) plane at negative \( x \)
negativeFaceXY [4] : Rectangular Acts::PlaneSurface, parallel to \( zx \) plane at negative \( y \)
positiveFaceXY [5] : Rectangular Acts::PlaneSurface, parallel to \( zx \) plane at positive \( y \)
Public Types
-
enum BoundValues
for streaming and access
Values:
-
enumerator eHalfLengthX
-
enumerator eHalfLengthY
-
enumerator eHalfLengthZ
-
enumerator eSize
-
enumerator eHalfLengthX
Public Functions
-
CuboidVolumeBounds() = delete
-
CuboidVolumeBounds(const CuboidVolumeBounds &bobo)
Copy Constructor.
- Parameters
bobo – is the source volume bounds to be copied
-
inline CuboidVolumeBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor - from a fixed size array.
- Parameters
values – iw the bound values
-
CuboidVolumeBounds(double halex, double haley, double halez) noexcept(false)
Constructor - the box boundaries.
- Parameters
halex – is the half length of the cube in x
haley – is the half length of the cube in y
halez – is the half length of the cube in z
-
~CuboidVolumeBounds() override = default
-
virtual Volume::BoundingBox boundingBox(const Transform3 *trf = nullptr, const Vector3 &envelope = {0, 0, 0}, const Volume *entity = nullptr) const final
Construct bounding box for this shape.
- Parameters
trf – Optional transform
envelope – Optional envelope to add / subtract from min/max
entity – Entity to associate this bounding box with
- Returns
Constructed bounding box
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
inline virtual bool inside(const Vector3 &pos, double tol = 0.) const override
This method checks if position in the 3D volume frame is inside the cylinder.
- Parameters
pos – is the position in volume frame to be checked
tol – is the absolute tolerance to be applied
-
CuboidVolumeBounds &operator=(const CuboidVolumeBounds &bobo)
Assignment operator.
- Parameters
bobo – is the source volume bounds to be assigned
-
virtual OrientedSurfaces orientedSurfaces(const Transform3 &transform = Transform3::Identity()) const override
Oriented surfaces, i.e.
the decomposed boundary surfaces and the according navigation direction into the volume given the normal vector on the surface
It will throw an exception if the orientation prescription is not adequate
- Parameters
transform – is the 3D transform to be applied to the boundary surfaces to position them in 3D space
- Returns
a vector of surfaces bounding this volume
-
virtual std::ostream &toStream(std::ostream &sl) const override
Output Method for std::ostream.
- Parameters
sl – is ostream operator to be dumped into
-
inline virtual VolumeBounds::BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
class CuboidVolumeBuilder : public Acts::ITrackingVolumeBuilder
- #include <Acts/Geometry/CuboidVolumeBuilder.hpp>
This class builds a box detector with a configurable amount of surfaces in it.
The idea is to allow a quick configuration of a detector for mostly unit test applications. Therefore this class does not demand to be a universal construction factory but a raw first draft of the idea of factory that may be extended in the future.
Public Functions
-
CuboidVolumeBuilder() = default
Default constructor without a configuration.
-
inline CuboidVolumeBuilder(Config &cfg)
Constructor that sets the config.
- Parameters
cfg – [in] Configuration of the detector
-
std::pair<double, double> binningRange(const GeometryContext &gctx, const VolumeConfig &cfg) const
This function evaluates the minimum and maximum of the binning as given by the configurations of the surfaces and layers.
The ordering depends on the binning value specified in the configuration of the volume.
- Parameters
gctx – [in] the geometry context for this building
cfg – [in] Container with the given surfaces and layers
- Returns
Pair containing the minimum and maximum along the binning direction
-
std::shared_ptr<const Layer> buildLayer(const GeometryContext &gctx, LayerConfig &cfg) const
This function creates a layer with a surface encapsulated with a given configuration.
The surface gets a detector element attached if the template parameter is non-void.
- Parameters
gctx – [in] the geometry context for this building
cfg – [inout] Configuration of the layer and the surface
- Returns
Pointer to the created layer
-
std::shared_ptr<const Surface> buildSurface(const GeometryContext &gctx, const SurfaceConfig &cfg) const
This function creates a surface with a given configuration.
A detector element is attached if the template parameter is non-void.
- Parameters
gctx – [in] the geometry context for this building
cfg – [in] Configuration of the surface
- Returns
Pointer to the created surface
-
std::shared_ptr<TrackingVolume> buildVolume(const GeometryContext &gctx, VolumeConfig &cfg) const
This function creates a TrackingVolume with a configurable number of layers and surfaces.
Each surface gets a detector element attached if the template parameter is non-void.
- Parameters
gctx – [in] the geometry context for this building
cfg – [inout] Configuration of the TrackingVolume
- Returns
Pointer to the created TrackingVolume
-
inline void setConfig(Config &cfg)
Setter of the config.
- Parameters
cfg – [in] Configuration that is set
-
void sortVolumes(std::vector<std::pair<TrackingVolumePtr, Vector3>> &tapVec, BinningValue bValue) const
This function builds a world TrackingVolume based on a given configuration.
- Parameters
gctx – [in] the geometry context for this building
- Returns
Pointer to the created TrackingGeometry
-
struct Config
- #include <Acts/Geometry/CuboidVolumeBuilder.hpp>
This struct stores the configuration of the tracking geometry.
Public Members
-
std::vector<VolumeConfig> volumeCfg = {}
-
std::vector<VolumeConfig> volumeCfg = {}
-
struct LayerConfig
- #include <Acts/Geometry/CuboidVolumeBuilder.hpp>
This struct stores the data for the construction of a PlaneLayer.
Public Members
-
bool active = false
-
size_t binsY = 1
-
size_t binsZ = 1
-
std::array<ActsScalar, 2u> envelopeX = {0, 0}
-
std::array<ActsScalar, 2u> envelopeY = {0, 0}
-
std::array<ActsScalar, 2u> envelopeZ = {0, 0}
-
std::optional<RotationMatrix3> rotation = {std::nullopt}
-
std::vector<SurfaceConfig> surfaceCfg
-
std::vector<std::shared_ptr<const Surface>> surfaces
-
bool active = false
-
struct SurfaceConfig
- #include <Acts/Geometry/CuboidVolumeBuilder.hpp>
This struct stores the data for the construction of a single PlaneSurface.
Public Members
-
std::function<DetectorElementBase*(const Transform3&, std::shared_ptr<const RectangleBounds>, double)> detElementConstructor
-
Vector3 position
-
std::shared_ptr<const RectangleBounds> rBounds = nullptr
-
RotationMatrix3 rotation = RotationMatrix3::Identity()
-
std::shared_ptr<const ISurfaceMaterial> surMat = nullptr
-
double thickness = 0.
-
std::function<DetectorElementBase*(const Transform3&, std::shared_ptr<const RectangleBounds>, double)> detElementConstructor
-
struct VolumeConfig
- #include <Acts/Geometry/CuboidVolumeBuilder.hpp>
This struct stores the data for the construction of a cuboid TrackingVolume with a given number of PlaneLayers.
Public Members
-
std::vector<LayerConfig> layerCfg
-
std::vector<std::shared_ptr<const Layer>> layers
-
Vector3 length
-
std::string name = "Volume"
-
Vector3 position
-
std::vector<std::shared_ptr<TrackingVolume>> trackingVolumes
-
std::vector<VolumeConfig> volumeCfg
-
std::shared_ptr<const IVolumeMaterial> volumeMaterial = nullptr
-
std::vector<LayerConfig> layerCfg
-
CuboidVolumeBuilder() = default
-
class CugraphTrackBuilding : public Acts::TrackBuildingBase
- #include <Acts/Plugins/ExaTrkX/CugraphTrackBuilding.hpp>
Public Functions
-
inline CugraphTrackBuilding(std::unique_ptr<const Logger> logger)
-
virtual std::vector<std::vector<int>> operator()(std::any nodes, std::any edges, std::any edge_weights, std::vector<int> &spacepointIDs) override
Perform track building.
- Parameters
nodes – Node tensor with shape (n_nodes, n_node_features)
edges – Edge-index tensor with shape (2, n_edges)
edgeWeights – Edge-weights of the previous edge classification phase
spacepointIDs – IDs of the nodes (must have size=n_nodes)
- Returns
tracks (as vectors of node-IDs)
-
inline CugraphTrackBuilding(std::unique_ptr<const Logger> logger)
-
class CutoutCylinderVolumeBounds : public Acts::VolumeBounds
- #include <Acts/Geometry/CutoutCylinderVolumeBounds.hpp>
Class which implements a cutout cylinder.
This shape is basically a cylinder, with another, smaller cylinder subtracted from the center. ——————— rmax | | | |———| | rmed | | | | —— —— rmin — hlZc — ——— hlZ —-—
Public Types
-
enum BoundValues
for streaming and access
Values:
-
enumerator eMinR
-
enumerator eMedR
-
enumerator eMaxR
-
enumerator eHalfLengthZ
-
enumerator eHalfLengthZcutout
-
enumerator eSize
-
enumerator eMinR
Public Functions
-
CutoutCylinderVolumeBounds() = delete
-
inline CutoutCylinderVolumeBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor - from a fixed size array.
- Parameters
values – The bound values
-
inline CutoutCylinderVolumeBounds(double rmin, double rmed, double rmax, double hlZ, double hlZc) noexcept(false)
Constructor from defining parameters.
- Parameters
rmin – Minimum radius at the “choke points”
rmed – The medium radius (outer radius of the cutout)
rmax – The outer radius of the overall shape
hlZ – The longer halflength of the shape
hlZc – The cutout halflength of the shape
-
~CutoutCylinderVolumeBounds() override = default
-
virtual Volume::BoundingBox boundingBox(const Transform3 *trf = nullptr, const Vector3 &envelope = {0, 0, 0}, const Volume *entity = nullptr) const final
Construct bounding box for this shape.
- Parameters
trf – Optional transform
envelope – Optional envelope to add / subtract from min/max
entity – Entity to associate this bounding box with
- Returns
Constructed bounding box
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
virtual bool inside(const Vector3 &gpos, double tol = 0) const override
Inside method to test whether a point is inside the shape.
- Parameters
gpos – The point to test
tol – The tolerance to test with
- Returns
Whether the point is inside or not.
-
virtual OrientedSurfaces orientedSurfaces(const Transform3 &transform = Transform3::Identity()) const override
Oriented surfaces, i.e.
the decomposed boundary surfaces and the according navigation direction into the volume given the normal vector on the surface
It will throw an exception if the orientation prescription is not adequate
- Parameters
transform – is the 3D transform to be applied to the boundary surfaces to position them in 3D space
- Returns
a vector of surfaces bounding this volume
-
virtual std::ostream &toStream(std::ostream &sl) const override
Write information about this instance to an outstream.
- Parameters
sl – The outstream
- Returns
The outstream
-
inline virtual VolumeBounds::BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
enum BoundValues
-
class CylinderBounds : public Acts::SurfaceBounds
- #include <Acts/Surfaces/CylinderBounds.hpp>
Bounds for a cylindrical Surface.
These bounds may be used for a CylinderSurface In case of bounds for a StraightLineSurface the radius determines the radius within a localPosition is regarded as inside bounds.
CylinderBounds also enhance the possibility of a cylinder segment with an opening angle \( 2\cdot\phi_{half}\) around an average \( \phi \) angle \( \phi_{ave} \).
CylinderBounds also supports beveled sides defined by an angle. Different angles can be defined on both sides of the cylinder. A positive angle is defined as “extruding” from the defined Zlength, while a negative angle is “intruding” on the Zlength.
- - +
\ | / \ | / \ | / \ | / |/______________|/ 2 * ZhalfLength
Public Types
-
enum BoundValues
Values:
-
enumerator eR
-
enumerator eHalfLengthZ
-
enumerator eHalfPhiSector
-
enumerator eAveragePhi
-
enumerator eBevelMinZ
-
enumerator eBevelMaxZ
-
enumerator eSize
-
enumerator eR
Public Functions
-
CylinderBounds() = delete
-
inline CylinderBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor - from fixed size array.
- Parameters
values – The parameter values
-
inline CylinderBounds(double r, double halfZ, double halfPhi = M_PI, double avgPhi = 0., double bevelMinZ = 0., double bevelMaxZ = 0.) noexcept(false)
Constructor - full cylinder.
- Parameters
r – The radius of the cylinder
halfZ – The half length in z
halfPhi – The half opening angle
avgPhi – (optional) The phi value from which the opening angle spans
bevelMinZ – (optional) The bevel on the negative z side
bevelMaxZ – (optional) The bevel on the positive z sid The bevel on the positive z side
-
~CylinderBounds() override = default
-
inline bool coversFullAzimuth() const
Returns true for full phi coverage.
-
std::vector<Vector3> createCircles(const Transform3 trans, size_t lseg) const
Create the bows/circles on either side of the cylinder.
- Parameters
trans – is the global transform
lseg – are the numbero if phi segments
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck) const final
Inside check for the bounds object driven by the boundary check directive Each Bounds has a method inside, which checks if a LocalPosition is inside the bounds Inside can be called without/with tolerances.
- Parameters
lposition – Local position (assumed to be in right surface frame)
bcheck – boundary check directive
- Returns
boolean indicator for the success of this operation
-
bool inside3D(const Vector3 &position, const BoundaryCheck &bcheck = true) const
Specialized method for CylinderBounds that checks if a global position is within the cylinder cover.
- Parameters
position – is the position in the cylinder frame
bcheck – is the boundary check directive
- Returns
boolean indicator for operation success
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
-
virtual BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
class CylinderLayer : public Acts::CylinderSurface, public Acts::Layer
- #include <Acts/Geometry/CylinderLayer.hpp>
Class to describe a cylindrical detector layer for tracking, it inhertis from both, Layer base class and CylinderSurface class.
Public Functions
-
CylinderLayer() = delete
-
CylinderLayer(const CylinderLayer &cla) = delete
-
~CylinderLayer() override = default
-
CylinderLayer &operator=(const CylinderLayer&) = delete
-
virtual const CylinderSurface &surfaceRepresentation() const override
Transforms the layer into a Surface representation This is for positioning and extrapolation.
-
virtual CylinderSurface &surfaceRepresentation() override
Public Static Functions
Factory for shared Layer pointer create a shared, fully deployed CylinderLayer.
- Parameters
transform – is the 3D transform that places the layer in 3D space
cbounds – are the cylindrical bounds of the layer
surfaceArray – is the Binned Array that holds the sensitive surfaces
thickness – is the layer thickness (along the normal)
ad – is the approach descriptor for approaching the layer
laytyp – is the layer type
- Returns
The return object is a shared pointer to the layer.
-
CylinderLayer() = delete
-
class CylinderSurface : public Acts::Surface
- #include <Acts/Surfaces/CylinderSurface.hpp>
Class for a CylinderSurface in the TrackingGeometry.
It inherits from Surface.
The cylinder surface has a special role in the TrackingGeometry, since it builds the surfaces of all TrackingVolumes at container level for a cylindrical tracking geometry.
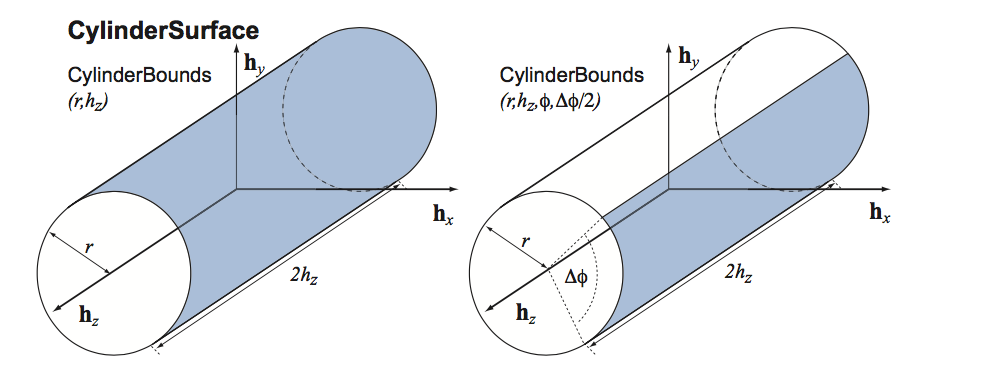
Subclassed by Acts::CylinderLayer
Public Functions
-
CylinderSurface() = delete
-
~CylinderSurface() override = default
-
virtual AlignmentToPathMatrix alignmentToPathDerivative(const GeometryContext &gctx, const FreeVector ¶meters) const final
Calculate the derivative of path length at the geometry constraint or point-of-closest-approach w.r.t.
alignment parameters of the surface (i.e. local frame origin in global 3D Cartesian coordinates and its rotation represented with extrinsic Euler angles)
- Parameters
gctx – The current geometry context object, e.g. alignment
parameters – is the free parameters
- Returns
Derivative of path length w.r.t. the alignment parameters
-
virtual Vector3 binningPosition(const GeometryContext &gctx, BinningValue bValue) const final
The binning position method - is overloaded for r-type binning.
- Parameters
gctx – The current geometry context object, e.g. alignment
bValue – is the type of global binning to be done
- Returns
is the global position to be used for binning
-
virtual const CylinderBounds &bounds() const final
This method returns the CylinderBounds by reference.
-
virtual Result<Vector2> globalToLocal(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, double tolerance = s_onSurfaceTolerance) const final
Global to local transformation.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the global position to be transformed
direction – is the global momentum direction (ignored in this operation)
tolerance – optional tolerance within which a point is considered valid on surface
- Returns
a Result<Vector2> which can be !ok() if the operation fails
-
virtual SurfaceIntersection intersect(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck = false, ActsScalar tolerance = s_onSurfaceTolerance) const final
Straight line intersection schema from position/direction.
If possible returns both solutions for the cylinder
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The position to start from
direction – The direction at start
bcheck – the Boundary Check
tolerance – the tolerance used for the intersection
- Returns
SurfaceIntersection object (contains intersection & surface)
-
virtual ActsMatrix<2, 3> localCartesianToBoundLocalDerivative(const GeometryContext &gctx, const Vector3 &position) const final
Calculate the derivative of bound track parameters local position w.r.t.
position in local 3D Cartesian coordinates
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The position of the parameters in global
- Returns
Derivative of bound local position w.r.t. position in local 3D cartesian coordinates
-
virtual Vector3 localToGlobal(const GeometryContext &gctx, const Vector2 &lposition, const Vector3 &direction) const final
Local to global transformation.
- Parameters
gctx – The current geometry context object, e.g. alignment
lposition – is the local position to be transformed
direction – is the global momentum direction (ignored in this operation)
- Returns
The global position by value
-
virtual std::string name() const override
Return method for properly formatted output string.
-
inline Vector3 normal(const GeometryContext &gctx) const
Normal vector return without argument.
-
virtual Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const final
Return method for surface normal information.
Note
for a Cylinder a local position is always required for the normal vector
- Parameters
gctx – The current geometry context object, e.g. alignment
lposition – is the local position for which the normal vector is requested
- Returns
normal vector at the local position by value
-
Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const = 0
Normal vector return without argument.
-
Vector3 normal(const GeometryContext &gctx, const Vector3 &position) const
Normal vector return without argument.
-
virtual Vector3 normal(const GeometryContext &gctx, const Vector3 &position) const final
Return method for surface normal information.
Note
for a Cylinder a local position is always required for the normal vector
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the global position for which the normal vector is requested
- Returns
normal vector at the global position by value
-
CylinderSurface &operator=(const CylinderSurface &other)
Assignment operator.
- Parameters
other – is the source cylinder for the copy
-
virtual double pathCorrection(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const final
Path correction due to incident of the track.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the global position as a starting point
direction – is the global momentum direction at the starting point
- Returns
is the correction factor due to incident
-
virtual Polyhedron polyhedronRepresentation(const GeometryContext &gctx, size_t lseg) const override
Return a Polyhedron for a cylinder.
- Parameters
gctx – The current geometry context object, e.g. alignment
lseg – Number of segments along curved lines, it represents the full 2*M_PI coverange, if lseg is set to 1 only the extrema are given
- Returns
A list of vertices and a face/facett description of it
-
virtual RotationMatrix3 referenceFrame(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const final
Return the measurement frame - this is needed for alignment, in particular The measurement frame of a cylinder is the tangential plane at a given position.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the position where the measurement frame is defined
direction – is the momentum direction vector (ignored)
- Returns
rotation matrix that defines the measurement frame
-
virtual Vector3 rotSymmetryAxis(const GeometryContext &gctx) const
Return method for the rotational symmetry axis.
- Parameters
gctx – The current geometry context object, e.g. alignment
- Returns
the z-Axis of transform
-
virtual SurfaceType type() const override
Return the surface type.
-
CylinderSurface() = delete
-
class CylinderVolumeBounds : public Acts::VolumeBounds
- #include <Acts/Geometry/CylinderVolumeBounds.hpp>
[0] and [1] at positive \( \phi \)
Bounds for a cylindrical Volume, the orientedSurfaces(..) method creates a vector of up to 6 surfaces:
case A) 3 Surfaces (full cylindrical tube): BoundarySurfaceFace [index]:
negativeFaceXY [0] : Acts::DiscSurface with \( r_{inner}=0 \), parallel to \( xy \) plane at negative \( z\)
positiveFaceXY [1] : Acts::DiscSurface with \( r_{inner}=0 \), parallel to \( xy \) plane at positive \( z\)
cylinderCover [2] : Acts::CylinderSurface confining the Acts::Volume
case B) 4 Surfaces (tube with inner and outer radius): BoundarySurfaceFace [index]:
negativeFaceXY [0] : Acts::DiscSurface with \( r_{inner}>0 \), parallel to \( xy \) plane at negative \( z\)
positiveFaceXY [1] : Acts::DiscSurface with \( r_{inner}>0 \), parallel to \( xy \) plane at positive \( z\)
tubeOuterCover [2] : Acts::CylinderSurface with \( r = r_{outer} \)
tubeInnerCover [3] : Acts::CylinderSurface with \( r = r_{inner} \)
case C) 6 Surfaces (sectoral tube with inner and outer radius): BoundarySurfaceFace [index]:
negativeFaceXY [0] : Acts::DiscSurface with \( r_{inner}>0\) and \( \phi < \pi \), parallel to \( xy \) plane at negative \(z\)
positiveFaceXY [1] : Acts::DiscSurface with \( r_{inner}>0 \) and \( \phi < \pi \), parallel to \( xy \) plane at positive \(z\)
tubeSectorOuterCover [2] : Acts::CylinderSurface with \( r = r_{outer}\)
tubeSectorInnerCover [3] : Acts::CylinderSurface with \( r = r_{inner} \)
tubeSectorNegativePhi [4] : Rectangular Acts::PlaneSurface attached to [0] and [1] at negative \( \phi \)
tubeSectorNegativePhi [5] :
Public Types
-
enum BoundValues
for streaming and access
Values:
-
enumerator eMinR
-
enumerator eMaxR
-
enumerator eHalfLengthZ
-
enumerator eHalfPhiSector
-
enumerator eAveragePhi
-
enumerator eBevelMinZ
-
enumerator eBevelMaxZ
-
enumerator eSize
-
enumerator eMinR
Public Functions
-
CylinderVolumeBounds() = delete
-
CylinderVolumeBounds(const CylinderBounds &cBounds, double thickness) noexcept(false)
Constructor - extruded from cylinder bounds and thickness.
- Parameters
cBounds – the cylinder bounds
thickness – of the extrusion
-
CylinderVolumeBounds(const CylinderVolumeBounds &cylbo) = default
Copy Constructor.
- Parameters
cylbo – is the source cylinder volume bounds for the copy
-
CylinderVolumeBounds(const RadialBounds &rBounds, double thickness) noexcept(false)
Constructor - extruded from radial bounds and thickness.
- Parameters
rBounds – the Radial bounds
thickness –
-
inline CylinderVolumeBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor - from a fixed size array.
- Parameters
values – The bound values
-
inline CylinderVolumeBounds(double rmin, double rmax, double halfz, double halfphi = M_PI, double avgphi = 0., double bevelMinZ = 0., double bevelMaxZ = 0.) noexcept(false)
Constructor.
- Parameters
rmin – The inner radius of the cylinder
rmax – The outer radius of the cylinder
halfz – The half length in z
halfphi – The half lopening angle
avgphi – The average phi value
bevelMinZ – The bevel angle, in radians, for the negative side
bevelMaxZ – The bevel angle, in radians, for the positive side
-
~CylinderVolumeBounds() override = default
-
inline virtual double binningBorder(BinningValue bValue) const override
Binning borders in double.
- Parameters
bValue – is the type used for the binning
-
inline virtual Vector3 binningOffset(BinningValue bValue) const override
Binning offset - overloaded for some R-binning types.
- Parameters
bValue – is the type used for the binning
-
virtual Volume::BoundingBox boundingBox(const Transform3 *trf = nullptr, const Vector3 &envelope = {0, 0, 0}, const Volume *entity = nullptr) const final
Construct bounding box for this shape.
- Parameters
trf – Optional transform
envelope – Optional envelope to add / subtract from min/max
entity – Entity to associate this bounding box with
- Returns
Constructed bounding box
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
inline virtual bool inside(const Vector3 &pos, double tol = 0.) const override
This method checks if position in the 3D volume frame is inside the cylinder.
- Parameters
pos – is a global position to be checked
tol – is the tolerance for the check
-
CylinderVolumeBounds &operator=(const CylinderVolumeBounds &cylbo) = default
-
virtual OrientedSurfaces orientedSurfaces(const Transform3 &transform = Transform3::Identity()) const override
Oriented surfaces, i.e.
the decomposed boundary surfaces and the according navigation direction into the volume given the normal vector on the surface
It will throw an exception if the orientation prescription is not adequate
- Parameters
transform – is the 3D transform to be applied to the boundary surfaces to position them in 3D space
- Returns
a vector of surfaces bounding this volume
-
virtual std::ostream &toStream(std::ostream &sl) const override
Output Method for std::ostream.
-
inline virtual VolumeBounds::BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
class CylinderVolumeBuilder : public Acts::ITrackingVolumeBuilder
- #include <Acts/Geometry/CylinderVolumeBuilder.hpp>
A volume builder to be used for building a concentrical cylindrical volumes.
a) configured volume
b) wrapping around a cylindrical/disk layer config
All are optionally wrapped around a given volume which has to by a cylinder volume and which has to be center at z == 0
To receive the tracking volume it is possible to also hand over a triple of layers, which is a C++ tuple of three pointers to layer vectors (defined in the ITrackingVolumeBuilder). This functionality is needed for a possible translation of an geometry existing in another format. The first entry represents the layers of the negative endcap, the second the layers of the barrel and the third the layers of the positive endcap. If the one of these pointers is a nullptr no layers will be created for this volume
For the endcap region it is possible to check for a ring layout, in which case an attempt to split into individual ring volumes is done
Public Functions
-
CylinderVolumeBuilder(const Config &cvbConfig, std::unique_ptr<const Logger> logger = getDefaultLogger("CylinderVolumeBuilder", Logging::INFO))
Constructor.
- Parameters
cvbConfig – [in] is the configuration struct to steer the builder
logger – [in] logging instance
-
~CylinderVolumeBuilder() override
Destructor.
-
VolumeConfig analyzeContent(const GeometryContext &gctx, const LayerVector &lVector, const MutableTrackingVolumeVector &mtvVector) const
Analyze the config to gather needed dimension.
- Parameters
gctx – [in] the geometry context for this building
lVector – [in] is the vector of layers that are parsed
mtvVector – [in] Vector of mutable tracking volumes to analyze
- Returns
a VolumeConfig representing this layer
-
inline Config getConfiguration() const
Get configuration method.
Return the configuration object.
- Returns
a copy of the config object
-
void setConfiguration(const Config &cvbConfig)
Set configuration method.
- Parameters
cvbConfig – [in] is the new configuration to be set
-
void setLogger(std::unique_ptr<const Logger> newLogger)
set logging instance
- Parameters
newLogger – [in] is the logging instance to be set
-
virtual MutableTrackingVolumePtr trackingVolume(const GeometryContext &gctx, TrackingVolumePtr existingVolume = nullptr, VolumeBoundsPtr externalBounds = nullptr) const override
CylinderVolumeBuilder main call method.
- Parameters
gctx – [in] geometry context for which this cylinder volume is built
existingVolume – [in] is an (optional) volume to be included
externalBounds – [in] are (optional) external confinement constraints
- Returns
a mutable pointer to a new TrackingVolume which includes the optionally provided existingVolume consistently for further processing
-
struct Config
- #include <Acts/Geometry/CylinderVolumeBuilder.hpp>
Nested configuration struct for this CylinderVolumeBuilder.
Public Members
-
std::array<std::shared_ptr<const ISurfaceMaterial>, 6> boundaryMaterial{nullptr, nullptr, nullptr, nullptr, nullptr, nullptr}
—————–— MB (outer [1]) ————— | MB [2] NEC MB [3] | B | MB [4] PEC MB [5] | —————–— MB (inner [0]) —————
-
bool buildToRadiusZero = false
Build the volume to the beam line.
-
bool checkRingLayout = false
Check for endcap ring layout.
-
std::shared_ptr<const IConfinedTrackingVolumeBuilder> ctVolumeBuilder = nullptr
Builder to construct confined volumes within the volume.
-
std::shared_ptr<const ILayerBuilder> layerBuilder = nullptr
Builder to construct layers within the volume.
-
std::pair<double, double> layerEnvelopeR = {1. * UnitConstants::mm, 1. * UnitConstants::mm}
Additional envelope in R to create rMin, rMax.
-
double layerEnvelopeZ = 1. * UnitConstants::mm
the additional envelope in Z to create zMin, zMax
-
double ringTolerance = 0 * UnitConstants::mm
Tolerance for endcap ring association.
-
std::shared_ptr<const ITrackingVolumeHelper> trackingVolumeHelper = nullptr
The tracking volume helper for construction.
-
std::shared_ptr<const IVolumeMaterial> volumeMaterial = nullptr
The world material.
-
std::string volumeName = ""
The string based indenfication.
-
int volumeSignature = -1
Volume signature.
-
std::array<std::shared_ptr<const ISurfaceMaterial>, 6> boundaryMaterial{nullptr, nullptr, nullptr, nullptr, nullptr, nullptr}
-
class CylinderVolumeHelper : public Acts::ITrackingVolumeHelper
- #include <Acts/Geometry/CylinderVolumeHelper.hpp>
The concrete implementation for cylindrical TrackingVolume objects of the ITrackingVolumeCreator interface.
Public Functions
-
CylinderVolumeHelper(const Config &cvhConfig, std::unique_ptr<const Logger> logger = getDefaultLogger("CylinderVolumeHelper", Logging::INFO))
Constructor.
- Parameters
cvhConfig – is the configuration struct for this builder
logger – logging instance
-
~CylinderVolumeHelper() override = default
-
virtual MutableTrackingVolumePtr createContainerTrackingVolume(const GeometryContext &gctx, const TrackingVolumeVector &volumes) const override
Create a container volumes from sub volumes, input volumes are ordered in R or Z by convention.
- Parameters
gctx – [in] the geometry context for this building
volumes – the volumes to be contained
- Returns
shared pointer to a new TrackingVolume
Create a gap volume from dimensions and.
- Parameters
gctx – [in] the geometry context for this building
mtvVector – Vector of confined TrackingVolumes
volumeMaterial – dense material properties for this TrackingVolume
rMin – minimum radius
rMax – maximum radius
zMin – minimum z
zMax – maximum z
layerPositions – custom layer positions
cylinder – type of layers
volumeName – : volume name to be given
bType – (optional) BinningType - arbitrary(default) or equidistant
- Returns
shared pointer to a new TrackingVolume
Create a gap volume from dimensions and.
Note
this TrackingVolume is restricted to Translation only
- Parameters
gctx – [in] the geometry context for this building
mtvVector – Vector of confined TrackingVolumes
volumeMaterial – dense material properties for this TrackingVolume
rMin – minimum radius
rMax – maximum radius
zMin – minimum z
zMax – maximum z
materialLayers – number of material layers (equidistant binning)
cylinder – type of layers
volumeName – volume name to be given
- Returns
shared pointer to a new TrackingVolume
Create a TrackingVolume* from a set of layers and (optional) parameters.
- Parameters
gctx – is the geometry context for witch the volume is built
layers – vector of static layers confined by the TrackingVolume if no bounds or HepTransform is given, they define the size together with the volume enevlope parameters
volumeMaterial – material properties for this TrackingVolume
mtvVector – Vector of confined TrackingVolumes
rMin – minimum radius
rMax – maximum radius
zMin – minimum z
zMax – maximum z
volumeName – volume name to be given
bType – (optional) BinningType - arbitrary(default) or equidistant
- Returns
shared pointer to a new TrackingVolume
Create a TrackingVolume* from a set of layers and (optional) parameters.
- Parameters
gctx – is the geometry context for witch the volume is built
layers – vector of static layers confined by the TrackingVolume if no bounds or HepTransform is given, they define the size together with the volume enevlope parameters
volumeMaterial – material properties for this TrackingVolume
volumeBounds – confinement of this TrackingVolume
mtvVector – (optional) Vector of confined TrackingVolumes
transform – (optional) placement of this TrackingVolume
volumeName – volume name to be given
bType – (optional) BinningType - arbitrary(default) or equidistant
- Returns
shared pointer to a new TrackingVolume
-
inline Config getConfiguration() const
Get configuration method.
-
void setConfiguration(const Config &cvhConfig)
Set configuration method.
- Parameters
cvhConfig – is the configuration struct assigned
-
void setLogger(std::unique_ptr<const Logger> newLogger)
Set logging instance.
- Parameters
newLogger – is the logger instance to be set
-
struct Config
- #include <Acts/Geometry/CylinderVolumeHelper.hpp>
Nested configuration struct for this CylinderVolumeHelper.
Public Members
-
std::shared_ptr<const ILayerArrayCreator> layerArrayCreator = nullptr
a tool for coherent LayerArray creation
-
int passiveLayerPhiBins = 1
bins in phi for the passive layer
-
int passiveLayerRzBins = 100
bins in r/z for the passive layer
-
double passiveLayerThickness = 1
thickness of passive layers
-
std::shared_ptr<const ITrackingVolumeArrayCreator> trackingVolumeArrayCreator = nullptr
Helper Tool to create TrackingVolume.
-
std::shared_ptr<const ILayerArrayCreator> layerArrayCreator = nullptr
-
CylinderVolumeHelper(const Config &cvhConfig, std::unique_ptr<const Logger> logger = getDefaultLogger("CylinderVolumeHelper", Logging::INFO))
-
class DD4hepDetectorElement : public Acts::TGeoDetectorElement
- #include <Acts/Plugins/DD4hep/DD4hepDetectorElement.hpp>
DetectorElement class implementation for DD4hep geometry.
DetectorElement plugin for DD4hep detector elements. DD4hep is based on TGeo shapes, therefore the DD4hepDetectorElement inherits from TGeoDetectorElement. The full geometrical information is provided by the TGeoDetectorElement. The DD4hepDetectorElement extends the TGeoDetectorElement by containing a segmentation for the readout.
Public Types
-
using ContextType = GeometryContext
Broadcast the context type.
Public Functions
Constructor.
Example options are:
”XYZ” -> identical frame definition (default value)
”YZX” -> node y axis is tracking x axis, etc.
”XzY” -> negative node z axis is tracking y axis, etc.
Note
In the translation from a 3D geometry (TGeo) which only knows tubes to a 2D geometry (Tracking geometry) a distinction if the module should be described as a cylinder or a disc surface needs to be done. Since this information can not be taken just from the geometry description (both can be described as TGeoTubeSeg), one needs to set the flag ‘isDisc’ in case a volume with shape
TGeoTubeSegshould be translated to a disc surface. Per default it will be translated into a cylindrical surface.- Parameters
scalor – is the scale factor for unit conversion if needed
isDisc – in case the sensitive detector module should be translated as disc (e.g. for endcaps) this flag should be set to true
digitizationModule – Optional digitization configuration for the element
material – Optional material of detector element
detElement – The DD4hep DetElement which should be linked to a surface
axes – is the axis orientation with respect to the tracking frame it is a string of the three characters x, y and z (standing for the three axes) There is a distinction between capital and lower case characters :
capital -> positive orientation of the axis
lower case -> negative orientation of the axis
-
~DD4hepDetectorElement() override = default
-
using ContextType = GeometryContext
-
class DD4hepLayerBuilder : public Acts::ILayerBuilder
- #include <Acts/Plugins/DD4hep/DD4hepLayerBuilder.hpp>
build layers of one cylinder-endcap setup from DD4hep input
This class is an implementation of the Acts::ILayerBuilder, creating the central (layers of barrel), the negative and positive layers (layers of endcaps) of one hierarchy (e.g. PixelDetector, StripDetector,…) with input from DD4hep.
Public Functions
-
DD4hepLayerBuilder(const Acts::DD4hepLayerBuilder::Config &config, std::unique_ptr<const Logger> logger)
Constructor.
- Parameters
config – is the configuration struct
logger – is the logging instance
-
~DD4hepLayerBuilder() override
Destructor.
-
virtual const LayerVector centralLayers(const GeometryContext &gctx) const final
LayerBuilder interface method.
- Parameters
gctx – the geometry context for this build call
- Returns
the layers at the central sector
-
inline Config getConfiguration() const
get the configuration object
-
inline virtual const std::string &identification() const final
Name identification.
- Returns
the string based identification of this configuration
-
virtual const LayerVector negativeLayers(const GeometryContext &gctx) const final
LayerBuilder interface method.
- Parameters
gctx – the geometry context for this build call
- Returns
the layers at negative side
-
virtual const LayerVector positiveLayers(const GeometryContext &gctx) const final
LayerBuilder interface method.
- Parameters
gctx – the geometry context for this build call
- Returns
the layers at positive side
-
void setConfiguration(const Config &config)
set the configuration object
- Parameters
config – is the configuration struct
-
void setLogger(std::unique_ptr<const Logger> logger)
set logging instance
-
struct Config
- #include <Acts/Plugins/DD4hep/DD4hepLayerBuilder.hpp>
nested configuration struct for steering of the layer builder
Public Members
-
BinningType bTypePhi = equidistant
the binning type of the contained surfaces in phi (equidistant/arbitrary)
-
BinningType bTypeR = equidistant
the binning type of the contained surfaces in r (equidistant/arbitrary)
-
BinningType bTypeZ = equidistant
the binning type of the contained surfaces in z (equidistant/arbitrary)
-
std::vector<dd4hep::DetElement> centralLayers
the DD4hep::DetElements of the layers of the central volume (barrel)
Note
if the current volume has no layers this parameter will not be set
-
std::string configurationName = "undefined"
string based identification
-
double defaultThickness = UnitConstants::fm
In case no surfaces (to be contained by the layer) are handed over, the layer thickness will be set to this value.
- Attention
The default thickness should be set thin enough that no touching or overlapping with the next layer can happen.
Note
Layers containing surfaces per default are not allowed to be attached to each other (navigation will bail at this point). However, to allow material layers (not containing surfaces) to be attached to each other, this default thickness is needed. In this way, the layer will be thin (with space to the next layer), but the material will have the’real’ thickness.
-
std::shared_ptr<const LayerCreator> layerCreator = nullptr
layer creator which is internally used to build layers
-
std::vector<dd4hep::DetElement> negativeLayers
the DD4hep::DetElements of the layers of the negative volume (negative endcap)
Note
if the current volume has no endcaps or no layers this parameter will not be set
-
std::vector<dd4hep::DetElement> positiveLayers
the DD4hep::DetElements of the layers of the positive volume (positive endcap)
Note
if the current volume has no endcaps or no layers this parameter will not be set
-
BinningType bTypePhi = equidistant
-
DD4hepLayerBuilder(const Acts::DD4hepLayerBuilder::Config &config, std::unique_ptr<const Logger> logger)
-
class DD4hepVolumeBuilder : public Acts::IConfinedTrackingVolumeBuilder
- #include <Acts/Plugins/DD4hep/DD4hepVolumeBuilder.hpp>
build confined TrackingVolumes of one cylinder setup from DD4hep input.
This class is an implementation of the Acts::IConfinedTrackingVolumeBuilder, creating the central (volumes of barrel), the negative and positive volumes (volumes of endcaps) of one hierarchy (e.g. ECal, HCal…) with input from DD4hep.
Public Functions
-
DD4hepVolumeBuilder(const Acts::DD4hepVolumeBuilder::Config &config, std::unique_ptr<const Logger> logger)
Constructor.
- Parameters
config – [in] is the configuration struct
logger – [in] is the logging instance
-
~DD4hepVolumeBuilder() override
Destructor.
-
virtual MutableTrackingVolumeVector centralVolumes() const final
Builder method for cylindrical, confined volume.
- Returns
The vector of TrackingVolumes at the central sector
-
inline Config getConfiguration() const
Get the configuration object.
- Returns
The used configuration struct
-
inline virtual const std::string &identification() const final
Name identification.
- Returns
The string based identification of this configuration
-
void setConfiguration(const Config &config)
Set the configuration object.
- Parameters
config – [in] is the configuration struct
-
void setLogger(std::unique_ptr<const Logger> logger)
Set logging instance.
- Parameters
logger – [in] Logger in use
-
struct Config
- #include <Acts/Plugins/DD4hep/DD4hepVolumeBuilder.hpp>
Nested configuration struct for steering of the volume builder.
Public Members
-
std::vector<dd4hep::DetElement> centralVolumes
Vector of central confined volumes.
-
std::string configurationName = "undefined"
string based identification
-
std::vector<dd4hep::DetElement> centralVolumes
-
DD4hepVolumeBuilder(const Acts::DD4hepVolumeBuilder::Config &config, std::unique_ptr<const Logger> logger)
-
template<typename, typename H = void, DelegateType = DelegateType::NonOwning>
class Delegate
-
template<typename R, typename H, DelegateType O, typename ...Args>
class Delegate<R(Args...), H, O> - #include <Acts/Utilities/Delegate.hpp>
Delegate type that allows type erasure of a callable without allocation and with a single level of indirection.
This type can support:
a free function pointer
a pointer to a member function alongside an instance pointer
Note
Delegateby default does not assume ownership of the instance. In that case You need to ensure that the lifetime of the callable instance is longer than that of theDelegate. If you setOtoDelegateType::Owning, it will assume ownership.Note
Currently
Delegateonly supports callables that areconst- Template Parameters
R – Return type of the function signature
H – Holder type that is used to store an instance
O – Ownership type of the delegate: Owning or NonOwning
Args – Types of the arguments of the function signatures
Public Functions
-
Delegate() = default
-
template<typename Callable, typename = isNoFunPtr<Callable>>
Delegate(Callable&&) = delete Constructor from rvalue reference is deleted, should catch construction with temporary objects and thus invalid pointers.
-
template<typename Callable, typename = isNoFunPtr<Callable>>
inline Delegate(Callable &callable) Constructor with a possibly stateful function object.
Note
Delegatedoes not assume owner ship overcallable. You need to ensure it’s lifetime is longer than that ofDelegate.- Template Parameters
Callable – Type of the callable
- Parameters
callable – The callable (function object or lambda)
-
Delegate(const Delegate&) = default
-
Delegate(Delegate&&) = default
-
inline Delegate(function_type callable)
Constructor with an explicit runtime callable.
Note
The function signature requires the first argument of the callable is
const void*. i.e. if the signature of the delegate isvoid(int), the callable’s signature has to bevoid(const void*, int).- Parameters
callable – The runtime value of the callable
-
template<auto Callable>
inline void connect() Connect a free function pointer.
Note
The function pointer must be
constexprforDelegateto accept it- Template Parameters
Callable – The compile-time free function pointer
-
template<typename Callable, typename = isNoFunPtr<Callable>>
void connect(Callable&&) = delete Connection with rvalue reference is deleted, should catch assignment from temporary objects and thus invalid pointers.
-
template<typename Callable, typename = isNoFunPtr<Callable>>
inline void connect(Callable &callable) Assignment operator with possibly stateful function object.
Note
Delegatedoes not assume owner ship overcallable. You need to ensure it’s lifetime is longer than that ofDelegate.- Template Parameters
Callable – Type of the callable
- Parameters
callable – The callable (function object or lambda)
-
template<auto Callable, typename Type, DelegateType T = kOwnership, typename = std::enable_if_t<T == DelegateType::NonOwning>>
inline void connect(const Type *instance) Connect a member function to be called on an instance.
Note
Delegatedoes not assume owner ship overinstance. You need to ensure it’s lifetime is longer than that ofDelegate.- Template Parameters
Callable – The compile-time member function pointer
Type – The type of the instance the member function should be called on
- Parameters
instance – The instance on which the member function pointer should be called on
-
inline void connect(function_type callable)
Connect anything that is assignable to the function pointer.
Note
The function signature requires the first argument of the callable is
const void*. i.e. if the signature of the delegate isvoid(int), the callable’s signature has to bevoid(const void*, int).- Parameters
callable – The runtime value of the callable
-
template<auto Callable, typename Type>
inline void connect(std::unique_ptr<const Type> instance) Connect a member function to be called on an instance.
Note
Delegateassumes owner ship overinstance.- Template Parameters
Callable – The compile-time member function pointer
Type – The type of the instance the member function should be called on
- Parameters
instance – The instance on which the member function pointer should be called on
-
inline bool connected() const
Return whether this delegate is currently connected.
- Returns
True if this delegate is connected
-
inline void disconnect()
Disconnect this delegate, meaning it cannot be called anymore.
-
template<typename holder_t = holder_type, typename = std::enable_if_t<!std::is_same_v<holder_t, void>>>
inline const holder_type *instance() const
-
inline operator bool() const
Return whether this delegate is currently connected.
- Returns
True if this delegate is connected
-
inline return_type operator()(Args... args) const
The call operator that exposes the functionality of the
Delegatetype.- Parameters
args – The arguments to call the contained function with
- Returns
Return value of the contained function
-
template<typename Callable, typename = isNoFunPtr<Callable>>
void operator=(Callable&&) = delete Assignment operator from rvalue reference is deleted, should catch assignment from temporary objects and thus invalid pointers.
-
template<typename Callable, typename = isNoFunPtr<Callable>>
inline void operator=(Callable &callable) Assignment operator with possibly stateful function object.
Note
Delegatedoes not assume owner ship overcallable. You need to ensure it’s lifetime is longer than that ofDelegate.- Template Parameters
Callable – Type of the callable
- Parameters
callable – The callable (function object or lambda)
-
inline void operator=(function_type callable)
Assignment operator with an explicit runtime callable.
Note
The function signature requires the first argument of the callable is
const void*. i.e. if the signature of the delegate isvoid(int), the callable’s signature has to bevoid(const void*, int).- Parameters
callable – The runtime value of the callable
-
template<typename action_list_t = ActionList<>, typename aborter_list_t = AbortList<>>
struct DenseStepperPropagatorOptions : public Acts::PropagatorOptions<ActionList<>, AbortList<>> - #include <Acts/Propagator/DenseEnvironmentExtension.hpp>
Public Functions
-
DenseStepperPropagatorOptions(const DenseStepperPropagatorOptions<action_list_t, aborter_list_t> &dspo) = default
Copy Constructor.
-
inline DenseStepperPropagatorOptions(const GeometryContext &gctx, const MagneticFieldContext &mctx)
Constructor with GeometryContext.
- Parameters
gctx – The current geometry context object, e.g. alignment
mctx – The current magnetic fielc context object
-
template<typename extended_aborter_list_t>
inline DenseStepperPropagatorOptions<action_list_t, extended_aborter_list_t> extend(extended_aborter_list_t aborters) const Expand the Options with extended aborters.
- Template Parameters
extended_aborter_list_t – Type of the new aborter list
- Parameters
aborters – The new aborter list to be used (internally)
Public Members
-
bool includeGgradient = true
Boolean flag for inclusion of d(dEds)d(q/p) into energy loss.
-
bool meanEnergyLoss = true
Toggle between mean and mode evaluation of energy loss.
-
double momentumCutOff = 0.
Cut-off value for the momentum in SI units.
-
DenseStepperPropagatorOptions(const DenseStepperPropagatorOptions<action_list_t, aborter_list_t> &dspo) = default
-
class DiamondBounds : public Acts::PlanarBounds
- #include <Acts/Surfaces/DiamondBounds.hpp>
Bounds for a double trapezoidal (“diamond”), planar Surface.
Public Types
-
enum BoundValues
Values:
-
enumerator eHalfLengthXnegY
-
enumerator eHalfLengthXzeroY
-
enumerator eHalfLengthXposY
-
enumerator eHalfLengthYneg
-
enumerator eHalfLengthYpos
-
enumerator eSize
-
enumerator eHalfLengthXnegY
Public Functions
-
DiamondBounds() = delete
-
inline DiamondBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor - from fixed size array.
- Parameters
values – The parameter values
-
inline DiamondBounds(double halfXnegY, double halfXzeroY, double halfXposY, double halfYneg, double halfYpos) noexcept(false)
Constructor for convex hexagon symmetric about the y axis.
- Parameters
halfXnegY – is the halflength in x at minimal y
halfXzeroY – is the halflength in x at y = 0
halfXposY – is the halflength in x at maximal y
halfYneg – is the halflength into y < 0
halfYpos – is the halflength into y > 0
-
~DiamondBounds() override = default
-
virtual const RectangleBounds &boundingBox() const final
Bounding box parameters.
- Returns
rectangle bounds for a bounding box
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck) const final
Inside check for the bounds object driven by the boundary check directive Each Bounds has a method inside, which checks if a LocalPosition is inside the bounds Inside can be called without/with tolerances.
- Parameters
lposition – Local position (assumed to be in right surface frame)
bcheck – boundary check directive
- Returns
boolean indicator for the success of this operation
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
- Parameters
sl – is the ostream in which it is dumped
-
virtual BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
virtual std::vector<Vector2> vertices(unsigned int lseg = 1) const final
Return the vertices.
Note
the number of segments is ignored for this representation
- Parameters
lseg – the number of segments used to approximate and eventually curved line
- Returns
vector for vertices in 2D
-
enum BoundValues
-
struct DigitizationCell
- #include <Acts/Digitization/DigitizationCell.hpp>
pair of ints for definition of a cell
Public Functions
-
inline DigitizationCell(size_t ch0, size_t ch1, float d = 0.)
-
inline void addCell(const DigitizationCell &dc, bool analogueReadout)
To merge cells in case they are at the same position.
Note
this function is needed because possible derived classes may calculate the energy deposit differently. Furthermore this allows to apply an energy cut, because the energy deposit can also be stored for digital readout.
- Parameters
dc – the cell to be added to the current cell
analogueReadout – flag indicating if we have analgue readout
-
inline double depositedEnergy() const
the deposited energy
Note
this function is needed because possible derived classes may calculate the energy deposit differently. Furthermore this allows to apply an energy cut, because the energy deposit can also be stored for digital readout.
Public Members
-
size_t channel0 = 0
-
size_t channel1 = 1
-
float data = 0.
-
inline DigitizationCell(size_t ch0, size_t ch1, float d = 0.)
-
class DigitizationModule
- #include <Acts/Digitization/DigitizationModule.hpp>
Class that holds the surfaces for a planar digitization detector module.
It needs a descriptor to design different pixel/strixels/strip setups (with a segmentation class) in order to define the readout segmentation
The digitizaiton is done in the local frame of the surface.
The lorentz angle is assumed to be only in x-direction and constant for the module, it is measured from the local z-direction towards the local x-direction.
The readout direction defines the charge drift either: a) towards the surface at -halfThickness if readout is defined at -1 b) towards the surface at +halfThickness if readout is defined at +1
Conventions:
3D positions are within the 3D frame of the module
2D positions are corrected to parameter surface at the center of the module (and not the readout surface)
The lorenzShift is the correction from the readout surface to the parameter surface
Public Functions
Constructor from a Segmentation descriptor.
- Parameters
moduleSegmentation – is the segmentation descriptions
halfThickness – is the half thickness of the module
readoutDirection – is the readout drift direction
lorentzAngle – is the lorentz drift angle
energyThreshold – Optional energy threshold for digitization
analogue – Run analogue digitization (defaults to false)
-
virtual ~DigitizationModule() = default
Virtual Destructor.
-
inline bool analogue() const
Indicates if the readout of the module is analogue, default is digital.
-
inline const SurfacePtrVector &boundarySurfaces() const
Return the bounding surfaces including top and bottom.
-
const DigitizationCell cell(const Vector2 &position) const
Get the digitization cell from a position.
- Parameters
position – The position to query
- Returns
-
inline DigitizationStep digitizationStep(const Vector3 &start, const Vector3 &end) const
Fill the associated digitization cell from this start and end position, correct for lorentz effect if needed.
- Parameters
start – is the start position of the step
end – is the end position of the step
- Returns
the digitization step
-
inline double energyThreshold() const
Return the energy threshold per cell of the module.
-
inline double halfThickness() const
Return the module thickness.
-
inline double lorentzAngle() const
Return the lorentz Angle.
-
inline int readoutDirection() const
Return the readout direction.
-
inline const Segmentation &segmentation() const
return the segmenation
-
const SurfacePtrVector segmentationSurfaces(const DigitizationCell &entryCids, const DigitizationCell &exitCids) const
Return the internal test segmentation surfaces to test between entry and exit given by their cell id’s - the boundaries are not given.
- Parameters
entryCids – are the entry digitisation cell ids
exitCids – are the exit digitisation cell ids
- Returns
object is a vector of shared surfaces
-
inline const SurfacePtrVector &segmentationSurfacesX() const
Return all surfaces in X - excluding the boundaries.
-
inline const SurfacePtrVector &segmentationSurfacesY() const
Return all surfaces in Y - excluding the boundaries.
-
SurfacePtrVector stepSurfaces(const Vector3 &start, const Vector3 &end) const
Return the test surfaces between these points.
- Parameters
start – is the start position of the step
end – is the end position of the step
- Returns
stepSurfaces are the surfaces to test
-
class DigitizationSourceLink
- #include <Acts/Digitization/DigitizationSourceLink.hpp>
Source link to connect digitization clusters back to truth information.
Public Functions
-
DigitizationSourceLink() = default
Construct and invalid source link.
Must be default constructible to satisfy SourceLinkConcept.
-
DigitizationSourceLink(const DigitizationSourceLink&) = default
-
DigitizationSourceLink(DigitizationSourceLink&&) = default
-
inline DigitizationSourceLink(GeometryIdentifier gid, std::vector<std::size_t> indices = {})
Constructor from geometry identifier and truth indices.
- Parameters
gid – is the geometry identifier
indices – are the truth indices
-
inline GeometryIdentifier geometryId() const
-
inline const std::vector<std::size_t> &indices() const
Access all associated truth indices.
-
DigitizationSourceLink &operator=(const DigitizationSourceLink&) = default
-
DigitizationSourceLink &operator=(DigitizationSourceLink&&) = default
-
DigitizationSourceLink() = default
-
struct DigitizationStep
- #include <Acts/Digitization/DigitizationCell.hpp>
DigitizationStep for further handling.
Public Functions
-
inline DigitizationStep()
this is the cell position
Standard constructor
-
inline DigitizationStep(double sl, double dl, const DigitizationCell &dc, const Vector3 &entryP, const Vector3 &exitP, const Vector2 &projectedPosition, const Vector2 &cellPosition)
Constructor with arguments.
- Parameters
sl – step length of this step
dl – drift length of this step
dc – is the digitization zell (with indices)
entryP – is the entry position into the cell
exitP – is the exit position from the cell
projectedPosition – is the position on the readout surface
cellPosition – is the nominal position of the cell
Public Members
-
double driftLength = {0.}
this is the path length within the cell
-
DigitizationCell stepCell
this is the path length of the setp center to the readout surface
-
Vector2 stepCellCenter
this is the projected position at the readout surface
-
Vector3 stepEntry
this is the cell identifier of the segment
-
Vector3 stepExit
this is the Entry point into the segment
-
double stepLength = {0.}
-
Vector2 stepReadoutProjected
this is the Exit point from the segment
-
inline DigitizationStep()
-
class Direction
- #include <Acts/Definitions/Direction.hpp>
The direction is always with respect to a given momentum, surface normal or other general axes.
Public Functions
-
inline constexpr Direction() = default
-
inline constexpr Direction(Value value)
-
inline constexpr std::size_t index() const
Convert dir to index [0,1] which allows to store direction dependent objects in std::array<T, 2u>
- Returns
either 0 or 1
-
inline constexpr Direction invert() const
Reverse the direction.
- Returns
an opposite direction
-
inline constexpr bool operator!=(Direction other) const
-
inline constexpr bool operator==(Direction other) const
-
inline constexpr int sign() const
Turns the direction into a signed value.
- Returns
a signed value
-
std::string toString() const
Public Static Functions
-
static inline constexpr Direction fromIndex(std::size_t index)
Convert and index [0,1] to a direction e.g.
for sorting in std::array<T, 2u>
- Parameters
index – is the direction at input
-
static inline constexpr Direction fromScalar(ActsScalar scalar)
This turns a signed value into a direction.
Will assert on zero.
- Parameters
scalar – is the signed value
- Returns
a direction enum
-
static inline constexpr Direction fromScalarZeroAsPositive(ActsScalar scalar)
This turns a signed value into a direction and 0 will be handled as a positive direction.
Only use this when you are convinced that the 0 case is properly handled downstream.
- Parameters
scalar – is the signed value
- Returns
a direction enum
-
inline constexpr Direction() = default
- #include <Acts/Propagator/DirectNavigator.hpp>
DirectNavigator class.
This is a fully guided navigator that progresses through a pre-given sequence of surfaces.
This can either be used as a validation tool, for truth tracking, or track refitting
Public Types
The sequentially crossed surfaces.
Public Functions
Initialize call - start of propagation.
- Template Parameters
propagator_state_t – The state type of the propagagor
stepper_t – The type of stepper used for the propagation
- Parameters
state – [inout] is the propagation state object
stepper – [in] Stepper in use
Navigator post step call.
- Template Parameters
propagator_state_t – is the type of Propagatgor state
stepper_t – is the used type of the Stepper by the Propagator
- Parameters
state – [inout] is the mutable propagator state object
stepper – [in] Stepper in use
Navigator pre step call.
- Template Parameters
propagator_state_t – is the type of Propagatgor state
stepper_t – is the used type of the Stepper by the Propagator
- Parameters
state – [inout] is the mutable propagator state object
stepper – [in] Stepper in use
Reset state.
- Parameters
state – is the state to reset
ssurface – is the new starting surface
tsurface – is the target surface
- #include <Acts/Propagator/DirectNavigator.hpp>
Nested Actor struct, called Initializer.
This is needed for the initialization of the surface sequence
Public Types
Public Functions
Defaulting the constructor.
Actor operator call.
- Template Parameters
statet – Type of the full propagator state
stepper_t – Type of the stepper
navigator_t – Type of the navigator
- Parameters
state – the entire propagator state
r – the result of this Actor
Public Members
The Surface sequence.
- #include <Acts/Propagator/DirectNavigator.hpp>
Actor result / state.
Public Members
- #include <Acts/Propagator/DirectNavigator.hpp>
Nested State struct.
It acts as an internal state which is created for every propagation/extrapolation step and keep thread-local navigation information
Public Members
Navigation state - external interface: the current surface.
Navigation state: the current volume.
Navigation state - external interface: a break has been detected.
Iterator the next surface.
Externally provided surfaces - expected to be ordered along the path.
Navigation state - starting layer.
Navigation state - external interface: the start surface.
Navigation state: the start volume.
Navigation state - target layer.
Navigation state - external interface: target is reached.
Navigation state - external interface: the target surface.
Navigation state: the target volume.
-
class DiscBounds : public Acts::SurfaceBounds
- #include <Acts/Surfaces/DiscBounds.hpp>
common base class for all bounds that are in a r/phi frame
simply introduced to avoid wrong bound assignments to surfaces
Subclassed by Acts::AnnulusBounds, Acts::DiscTrapezoidBounds, Acts::RadialBounds
Public Functions
-
virtual double binningValuePhi() const = 0
Returns a refererance phi for binning.
-
virtual double binningValueR() const = 0
Returns a reference radius for binning.
-
virtual bool coversFullAzimuth() const = 0
Returns true for full phi coverage.
-
virtual bool insideRadialBounds(double R, double tolerance = 0.) const = 0
Checks if it’s inside the radius.
-
virtual double rMax() const = 0
Return method for outer Radius.
-
virtual double rMin() const = 0
Return method for inner Radius.
-
virtual std::vector<Vector2> vertices(unsigned int lseg) const = 0
Return the vertices.
Note
that the extremas are given, which may slightly alter the number of segments returned
- Parameters
lseg – the number of segments used to approximate and eventually curved line, the number refers to full 2*PI
- Returns
vector for vertices in 2D
-
class DiscLayer : public virtual Acts::DiscSurface, public Acts::Layer
- #include <Acts/Geometry/DiscLayer.hpp>
Class to describe a disc-like detector layer for tracking, it inhertis from both, Layer base class and DiscSurface class.
Public Functions
-
DiscLayer() = delete
-
DiscLayer(const DiscLayer &cla) = delete
-
~DiscLayer() override = default
-
virtual const DiscSurface &surfaceRepresentation() const override
Transforms the layer into a Surface representation for extrapolation.
- Returns
This method returns a surface reference
-
virtual DiscSurface &surfaceRepresentation() override
Public Static Functions
Factory constructor with DiscSurface components.
- Parameters
transform – is the transform to place the layer in the 3D frame
dbounds – are the disc bounds that describe the layer dimensions
surfaceArray – is the array of sensitive surfaces
thickness – is the layer thickness (along the normal vector)
ad – is the approach descriptor that provides the approach surface
laytyp – is the layer type
- Returns
a sharted pointer to the new layer
-
DiscLayer() = delete
-
class DiscSurface : public Acts::Surface
- #include <Acts/Surfaces/DiscSurface.hpp>
Class for a disc surface (or a segment thereof)
The DiscSurface is defined by the local polar coordinates \( (r,phi) \).
The surface transform positions the disc such that the origin is at \( r=0 \), independent of the provided
DiscBounds. The normal vector of the disc (i.e., the local \(z\)-axis) is given by \( \vec e_{z} = \vec e_{r} \times\vec e_{phi} \).The disc surface The only surface type for which the covariance matrix is NOT given in the reference frame. A conversion from polar to cartesian coordinates needs to happen to transfer the local coordinates onto the cartesian reference frame coordinates.
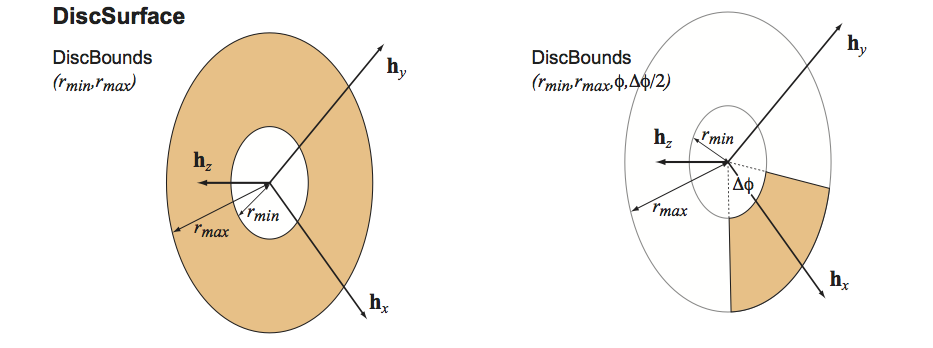
Subclassed by Acts::DiscLayer
Public Functions
-
DiscSurface() = delete
-
~DiscSurface() override = default
-
virtual Vector3 binningPosition(const GeometryContext &gctx, BinningValue bValue) const final
The binning position The position calculated for a certain binning type.
- Parameters
gctx – The current geometry context object, e.g. alignment
bValue – The binning type to be used
- Returns
position that can beused for this binning
-
virtual double binningPositionValue(const GeometryContext &gctx, BinningValue bValue) const final
Implement the binningValue.
Note
This calls the parent method except for binR
- Parameters
gctx – The current geometry context object, e.g. alignment
bValue – is the dobule in which you want to bin
- Returns
float to be used for the binning schema
-
virtual const SurfaceBounds &bounds() const final
This method returns the bounds by reference.
-
virtual BoundToFreeMatrix boundToFreeJacobian(const GeometryContext &gctx, const BoundVector &boundParams) const final
Calculate the jacobian from local to global which the surface knows best, hence the calculation is done here.
- Parameters
gctx – The current geometry context object, e.g. alignment
boundParams – is the bound parameters vector
- Returns
Jacobian from local to global
-
virtual FreeToBoundMatrix freeToBoundJacobian(const GeometryContext &gctx, const FreeVector ¶meters) const final
Calculate the jacobian from global to local which the surface knows best, hence the calculation is done here.
- Parameters
gctx – The current geometry context object, e.g. alignment
parameters – is the free parameters
- Returns
Jacobian from global to local
-
virtual Result<Vector2> globalToLocal(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, double tolerance = s_onSurfaceTolerance) const final
Global to local transformation.
Note
the direction is ignored for Disc surfaces in this calculateion
- Parameters
gctx – The current geometry context object, e.g. alignment
position – global 3D position - considered to be on surface but not inside bounds (check is done)
direction – global 3D momentum direction (optionally ignored)
tolerance – optional tolerance within which a point is considered valid on surface
- Returns
a Result<Vector2> which can be !ok() if the operation fails
-
Vector2 globalToLocalCartesian(const GeometryContext &gctx, const Vector3 &position, double tol = 0.) const
Special method for DiscSurface : global<->local from cartesian coordinates.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is a global cartesian 3D position
tol – The absolute tolerance parameter
- Returns
value is a local polar
-
virtual SurfaceIntersection intersect(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck = false, ActsScalar tolerance = s_onSurfaceTolerance) const final
Straight line intersection schema.
Mathematical motivation:
the equation of the plane is given by: \( \vec n \cdot \vec x = \vec n \cdot \vec p,\) where \( \vec n = (n_{x}, n_{y}, n_{z})\) denotes the normal vector of the plane, \( \vec p = (p_{x}, p_{y}, p_{z})\) one specific point on the plane and \( \vec x = (x,y,z) \)
all possible points on the plane.
Given a line with:
\( \vec l(u) = \vec l_{1} + u \cdot \vec v \),
the solution for
\( u \) can be written: \( u = \frac{\vec n (\vec p - \vec l_{1})}{\vec n \vec v}\) If the denominator is 0 then the line lies:either in the plane
perpendicular to the normal of the plane
Note
expected to be normalized (no checking)
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The global position as a starting point
direction – The global direction at the starting point
bcheck – The boundary check prescription
tolerance – the tolerance used for the intersection
- Returns
The SurfaceIntersection object
-
virtual ActsMatrix<2, 3> localCartesianToBoundLocalDerivative(const GeometryContext &gctx, const Vector3 &position) const final
Calculate the derivative of bound track parameters local position w.r.t.
position in local 3D Cartesian coordinates
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The position of the parameters in global
- Returns
Derivative of bound local position w.r.t. position in local 3D cartesian coordinates
-
Vector3 localCartesianToGlobal(const GeometryContext &gctx, const Vector2 &lposition) const
Special method for DiscSurface : local<->global transformation when provided cartesian coordinates.
- Parameters
gctx – The current geometry context object, e.g. alignment
lposition – is local 2D position in cartesian coordinates
- Returns
value is a global cartesian 3D position
-
Vector2 localCartesianToPolar(const Vector2 &lcart) const
Special method for Disc surface : local<->local transformations polar <-> cartesian.
- Parameters
lcart – is local 2D position in cartesian coordinates
- Returns
value is a local position in polar coordinates
-
Vector2 localPolarToCartesian(const Vector2 &lpolar) const
Special method for DiscSurface : local<->local transformations polar <-> cartesian.
- Parameters
lpolar – is a local position in polar coordinates
- Returns
values is local 2D position in cartesian coordinates
-
Vector2 localPolarToLocalCartesian(const Vector2 &locpol) const
Special method for DiscSurface : local<->local transformations polar <-> cartesian.
- Parameters
locpol – is a local position in polar coordinates
- Returns
values is local 2D position in cartesian coordinates
-
virtual Vector3 localToGlobal(const GeometryContext &gctx, const Vector2 &lposition, const Vector3 &direction) const final
Local to global transformation For planar surfaces the momentum direction is ignored in the local to global transformation.
- Parameters
gctx – The current geometry context object, e.g. alignment
lposition – local 2D position in specialized surface frame
direction – global 3D momentum direction (optionally ignored)
- Returns
global position by value
-
virtual std::string name() const override
Return properly formatted class name for screen output.
-
inline Vector3 normal(const GeometryContext &gctx) const
Normal vector return without argument.
-
virtual Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const final
Normal vector return.
- Parameters
gctx – The current geometry context object, e.g. alignment
lposition – The local position is ignored
- Returns
a Vector3 by value
-
Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const = 0
Normal vector return without argument.
-
Vector3 normal(const GeometryContext &gctx, const Vector3 &position) const
Normal vector return without argument.
-
DiscSurface &operator=(const DiscSurface &other)
Assignment operator.
- Parameters
other – The source sourface for the assignment
-
virtual double pathCorrection(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const final
Path correction due to incident of the track.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The global position as a starting point
direction – The global momentum direction at the starting point
- Returns
The correction factor due to incident
-
virtual Polyhedron polyhedronRepresentation(const GeometryContext &gctx, size_t lseg) const override
Return a Polyhedron for the surfaces.
- Parameters
gctx – The current geometry context object, e.g. alignment
lseg – Number of segments along curved lines, it represents the full 2*M_PI coverange, if lseg is set to 1 only the extrema are given
- Returns
A list of vertices and a face/facett description of it
-
virtual SurfaceType type() const override
Return the surface type.
-
DiscSurface() = delete
-
class DiscTrapezoidBounds : public Acts::DiscBounds
- #include <Acts/Surfaces/DiscTrapezoidBounds.hpp>
Class to describe the bounds for a planar DiscSurface.
By providing an argument for hphisec, the bounds can be restricted to a phi-range around the center position.
Public Types
-
enum BoundValues
Values:
-
enumerator eHalfLengthXminR
-
enumerator eHalfLengthXmaxR
-
enumerator eMinR
-
enumerator eMaxR
-
enumerator eAveragePhi
-
enumerator eStereo
-
enumerator eSize
-
enumerator eHalfLengthXminR
Public Functions
-
DiscTrapezoidBounds() = delete
-
inline DiscTrapezoidBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor - from fixed size array.
- Parameters
values – The parameter values
-
DiscTrapezoidBounds(double halfXminR, double halfXmaxR, double minR, double maxR, double avgPhi = M_PI_2, double stereo = 0.) noexcept(false)
Constructor for a symmetric Trapezoid giving min X length, max X length, Rmin and R max.
- Parameters
halfXminR – half length in X at min radius
halfXmaxR – half length in X at maximum radius
minR – inner radius
maxR – outer radius
avgPhi – average phi value
stereo – optional stero angle applied
-
~DiscTrapezoidBounds() override = default
-
inline virtual double binningValuePhi() const final
Return a reference phi for binning.
-
inline virtual double binningValueR() const final
Return a reference radius for binning.
-
inline virtual bool coversFullAzimuth() const final
Returns true for full phi coverage - obviously false here.
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
inline double halfLengthY() const
This method returns the half length in Y (this is Rmax -Rmin)
-
inline double halfPhiSector() const
This method returns the halfPhiSector which is covered by the disc.
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck = true) const final
This method checks if the radius given in the LocalPosition is inside [rMin,rMax] if only tol0 is given and additional in the phi sector is tol1 is given.
- Parameters
lposition – is the local position to be checked (in polar coordinates)
bcheck – is the boundary check directive
-
inline virtual bool insideRadialBounds(double R, double tolerance = 0.) const final
Checks if this is inside the radial coverage given the a tolerance.
-
inline double rCenter() const
This method returns the center radius.
-
inline virtual double rMax() const final
This method returns outer radius.
-
inline virtual double rMin() const final
This method returns inner radius.
-
inline double stereo() const
This method returns the stereo angle.
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
-
virtual SurfaceBounds::BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
virtual std::vector<Vector2> vertices(unsigned int lseg) const final
This method returns the xy coordinates of the four corners of the bounds in module coorindates (in xy)
Note
that the number of segments are ignored for this surface
- Parameters
lseg – the number of segments used to approximate and eventually curved line
- Returns
vector for vertices in 2D
-
enum BoundValues
-
template<class T>
class DistanceSorterT - #include <Acts/Geometry/GeometryObjectSorter.hpp>
This will check on absolute distance.
Public Functions
-
inline DistanceSorterT(BinningValue bValue, Vector3 reference)
Constructor from a binning value.
- Parameters
bValue – is the value in which the binning is done
reference – is the reference point
-
inline DistanceSorterT(BinningValue bValue, Vector3 reference)
-
template<typename input_track_t = BoundTrackParameters, typename linearizer_t = DummyTrackLinearizer>
class DummyVertexFitter - #include <Acts/Vertexing/DummyVertexFitter.hpp>
Dummy vertex fitter class, only to be used for ensuring interfaces where a vertex fitter type is required but no fitter is actually needed.
Public Types
-
using InputTrack_t = input_track_t
-
using Linearizer_t = linearizer_t
-
using Propagator_t = void
Public Functions
-
DummyVertexFitter() = delete
-
Result<Vertex<input_track_t>> fit(const std::vector<input_track_t>&, const linearizer_t&, const VertexingOptions<input_track_t>&) const
Dummy fit method.
-
using InputTrack_t = input_track_t
-
class EdgeClassificationBase
- #include <Acts/Plugins/ExaTrkX/Stages.hpp>
Subclassed by Acts::OnnxEdgeClassifier, Acts::TorchEdgeClassifier
Public Functions
-
virtual ~EdgeClassificationBase() = default
-
virtual std::tuple<std::any, std::any, std::any> operator()(std::any nodes, std::any edges) = 0
Perform edge classification.
- Parameters
nodes – Node tensor with shape (n_nodes, n_node_features)
edges – Edge-index tensor with shape (2, n_edges)
- Returns
(node_tensor, edge_tensor, score_tensor)
-
virtual ~EdgeClassificationBase() = default
-
template<typename extensionlist_t = StepperExtensionList<DefaultExtension>, typename auctioneer_t = detail::VoidAuctioneer>
class EigenStepper - #include <Acts/Propagator/EigenStepper.hpp>
Runge-Kutta-Nystroem stepper based on Eigen implementation for the following ODE:
r = (x,y,z) … global position T = (Ax,Ay,Az) … momentum direction (normalized)
dr/ds = T dT/ds = q/p * (T x B)
with s being the arc length of the track, q the charge of the particle, p the momentum magnitude and B the magnetic field
Public Types
-
using BoundState = std::tuple<BoundTrackParameters, Jacobian, double>
-
using Covariance = BoundSquareMatrix
-
using CurvilinearState = std::tuple<CurvilinearTrackParameters, Jacobian, double>
-
using Jacobian = BoundMatrix
Jacobian, Covariance and State definitions.
Public Functions
Constructor requires knowledge of the detector’s magnetic field.
-
inline double absoluteMomentum(const State &state) const
Absolute momentum accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
Result<BoundState> boundState(State &state, const Surface &surface, bool transportCov = true, const FreeToBoundCorrection &freeToBoundCorrection = FreeToBoundCorrection(false)) const
Create and return the bound state at the current position.
This transports (if necessary) the covariance to the surface and creates a bound state. It does not check if the transported state is at the surface, this needs to be guaranteed by the propagator
- Parameters
state – [in] State that will be presented as
BoundStatesurface – [in] The surface to which we bind the state
transportCov – [in] Flag steering covariance transport
freeToBoundCorrection – [in] Correction for non-linearity effect during transform from free to bound
- Returns
A bound state:
the parameters at the surface
the stepwise jacobian towards it (from last bound)
and the path length (from start - for ordering)
-
inline double charge(const State &state) const
Charge access.
- Parameters
state – [in] The stepping state (thread-local cache)
-
CurvilinearState curvilinearState(State &state, bool transportCov = true) const
Create and return a curvilinear state at the current position.
This transports (if necessary) the covariance to the current position and creates a curvilinear state.
- Parameters
state – [in] State that will be presented as
CurvilinearStatetransportCov – [in] Flag steering covariance transport
- Returns
A curvilinear state:
the curvilinear parameters at given position
the stepweise jacobian towards it (from last bound)
and the path length (from start - for ordering)
-
inline Vector3 direction(const State &state) const
Momentum direction accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline Result<Vector3> getField(State &state, const Vector3 &pos) const
Get the field for the stepping, it checks first if the access is still within the Cell, and updates the cell if necessary.
- Parameters
state – [inout] is the propagation state associated with the track the magnetic field cell is used (and potentially updated)
pos – [in] is the field position
-
inline double getStepSize(const State &state, ConstrainedStep::Type stype) const
Get the step size.
- Parameters
state – [in] The stepping state (thread-local cache)
stype – [in] The step size type to be returned
-
template<typename charge_t>
State makeState(std::reference_wrapper<const GeometryContext> gctx, std::reference_wrapper<const MagneticFieldContext> mctx, const GenericBoundTrackParameters<charge_t> &par, double ssize = std::numeric_limits<double>::max()) const
-
inline Vector3 momentum(const State &state) const
Momentum accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline std::string outputStepSize(const State &state) const
Output the Step Size - single component.
- Parameters
state – [in,out] The stepping state (thread-local cache)
-
inline double overstepLimit(const State&) const
Overstep limit.
-
inline Vector3 position(const State &state) const
Global particle position accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline double qOverP(const State &state) const
QoP direction accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline void releaseStepSize(State &state) const
Release the Step size.
- Parameters
state – [in,out] The stepping state (thread-local cache)
-
void resetState(State &state, const BoundVector &boundParams, const BoundSquareMatrix &cov, const Surface &surface, const double stepSize = std::numeric_limits<double>::max()) const
Resets the state.
- Parameters
state – [inout] State of the stepper
boundParams – [in] Parameters in bound parametrisation
cov – [in] Covariance matrix
surface – [in] The reference surface of the bound parameters
stepSize – [in] Step size
-
void setIdentityJacobian(State &state) const
Method that reset the Jacobian to the Identity for when no bound state are available.
- Parameters
state – [inout] State of the stepper
-
inline void setStepSize(State &state, double stepSize, ConstrainedStep::Type stype = ConstrainedStep::actor, bool release = true) const
Set Step size - explicitly with a double.
- Parameters
state – [in,out] The stepping state (thread-local cache)
stepSize – [in] The step size value
stype – [in] The step size type to be set
release – [in] Do we release the step size?
Perform a Runge-Kutta track parameter propagation step.
Note
The state contains the desired step size. It can be negative during backwards track propagation, and since we’re using an adaptive algorithm, it can be modified by the stepper class during propagation.
- Parameters
state – [inout] the propagation state
navigator – [in] the navigator of the propagation
-
inline double time(const State &state) const
Time access.
- Parameters
state – [in] The stepping state (thread-local cache)
-
void transportCovarianceToBound(State &state, const Surface &surface, const FreeToBoundCorrection &freeToBoundCorrection = FreeToBoundCorrection(false)) const
Method for on-demand transport of the covariance to a new curvilinear frame at current position, or direction of the state.
Note
no check is done if the position is actually on the surface
- Template Parameters
surface_t – the Surface type
- Parameters
state – [inout] State of the stepper
surface – [in] is the surface to which the covariance is forwarded to
freeToBoundCorrection – [in] Correction for non-linearity effect during transform from free to bound
-
void transportCovarianceToCurvilinear(State &state) const
Method for on-demand transport of the covariance to a new curvilinear frame at current position, or direction of the state.
- Parameters
state – [inout] State of the stepper
-
void update(State &state, const FreeVector &freeParams, const BoundVector &boundParams, const Covariance &covariance, const Surface &surface) const
Method to update a stepper state to the some parameters.
- Parameters
state – [inout] State object that will be updated
freeParams – [in] Free parameters that will be written into
stateboundParams – [in] Corresponding bound parameters used to update jacToGlobal in
statecovariance – [in] The covariance that will be written into
statesurface – [in] The surface used to update the jacToGlobal
-
void update(State &state, const Vector3 &uposition, const Vector3 &udirection, double qOverP, double time) const
Method to update the stepper state.
- Parameters
state – [inout] State object that will be updated
uposition – [in] the updated position
udirection – [in] the updated direction
qOverP – [in] the updated qOverP value
time – [in] the updated time value
-
template<typename object_intersection_t>
inline void updateStepSize(State &state, const object_intersection_t &oIntersection, bool release = true) const Update step size.
This method intersects the provided surface and update the navigation step estimation accordingly (hence it changes the state). It also returns the status of the intersection to trigger onSurface in case the surface is reached.
- Parameters
state – [in,out] The stepping state (thread-local cache)
oIntersection – [in] The ObjectIntersection to layer, boundary, etc
release – [in] boolean to trigger step size release
-
inline Intersection3D::Status updateSurfaceStatus(State &state, const Surface &surface, Direction navDir, const BoundaryCheck &bcheck, ActsScalar surfaceTolerance = s_onSurfaceTolerance, const Logger &logger = getDummyLogger()) const
Update surface status.
It checks the status to the reference surface & updates the step size accordingly
- Parameters
state – [inout] The stepping state (thread-local cache)
surface – [in] The surface provided
navDir – [in] The navigation direction
bcheck – [in] The boundary check for this status update
surfaceTolerance – [in] Surface tolerance used for intersection
logger – [in] A
Loggerinstance
-
struct State
- #include <Acts/Propagator/EigenStepper.hpp>
State for track parameter propagation.
It contains the stepping information and is provided thread local by the propagator
Public Functions
-
State() = delete
-
template<typename charge_t>
inline explicit State(const GeometryContext &gctx, MagneticFieldProvider::Cache fieldCacheIn, const GenericBoundTrackParameters<charge_t> &par, double ssize = std::numeric_limits<double>::max()) Constructor from the initial bound track parameters.
Note
the covariance matrix is copied when needed
- Template Parameters
charge_t – Type of the bound parameter charge
- Parameters
gctx – [in] is the context object for the geometry
fieldCacheIn – [in] is the cache object for the magnetic field
par – [in] The track parameters at start
ssize – [in] is the maximum step size
Public Members
-
double absCharge = UnitConstants::e
The absolute charge as the free vector can be 1/p or q/p.
-
auctioneer_t auctioneer
Auctioneer for choosing the extension.
-
Vector3 B_first
Magnetic field evaulations.
-
Vector3 B_last
-
Vector3 B_middle
-
Covariance cov = Covariance::Zero()
-
bool covTransport = false
Covariance matrix (and indicator) associated with the initial error on track parameters.
-
FreeVector derivative = FreeVector::Zero()
The propagation derivative.
-
extensionlist_t extension
List of algorithmic extensions.
-
MagneticFieldProvider::Cache fieldCache
This caches the current magnetic field cell and stays (and interpolates) within it as long as this is valid.
See step() code for details.
-
std::reference_wrapper<const GeometryContext> geoContext
The geometry context.
-
BoundToFreeMatrix jacToGlobal = BoundToFreeMatrix::Zero()
Jacobian from local to the global frame.
-
FreeMatrix jacTransport = FreeMatrix::Identity()
Pure transport jacobian part from runge kutta integration.
-
Vector3 k1
k_i of the RKN4 algorithm
-
Vector3 k2
-
Vector3 k3
-
Vector3 k4
-
std::array<double, 4> kQoP = {}
k_i elements of the momenta
-
FreeVector pars = FreeVector::Zero()
Internal free vector parameters.
-
double pathAccumulated = 0.
Accummulated path length state.
-
double previousStepSize = 0.
Last performed step (for overstep limit calculation)
-
struct Acts::EigenStepper::State::[anonymous] stepData
Storage of magnetic field and the sub steps during a RKN4 step.
-
ConstrainedStep stepSize
Adaptive step size of the runge-kutta integration.
-
State() = delete
-
using BoundState = std::tuple<BoundTrackParameters, Jacobian, double>
-
class ElementFraction
- #include <Acts/Material/MaterialComposition.hpp>
Memory-efficient storage of the relative fraction of an element.
This can be used to define materials that are compounds of multiple elements with varying fractions. The element is identified by its atomic number stored as a single byte (allows up to 256 elements; more than we need). Its fraction is also stored as a single byte with values between 0 and
This gives an accuracy of 1/256 ~ 0.5 %.
The element fraction allows you to store element composition in merged materials with a large number of bins. Depending on the detector and the description granularity this can be a lot of information and thus requires the reduced memory footprint. This is really only needed for nuclear interaction in the fast simulation where the reduced fractional accuracy is not a problem. The fractional accuracy should be much better than the parametrization uncertainty for hadronic interactions.
Public Functions
-
ElementFraction() = delete
Must always be created with valid data.
-
ElementFraction(const ElementFraction&) = default
-
ElementFraction(ElementFraction&&) = default
-
inline constexpr ElementFraction(unsigned int e, float f)
Construct from atomic number and relative fraction.
- Parameters
e – is the atomic number of the element
f – is the relative fraction and must be a value in [0,1]
-
inline explicit constexpr ElementFraction(unsigned int e, unsigned int w)
Construct from atomic number and integer weight.
- Parameters
e – is the atomic number of the element
w – is the integer weight and must be a value in [0,256)
-
~ElementFraction() = default
-
inline constexpr uint8_t element() const
The element atomic number.
-
inline constexpr float fraction() const
The relative fraction of this element.
-
ElementFraction &operator=(const ElementFraction&) = default
-
ElementFraction &operator=(ElementFraction&&) = default
-
class EllipseBounds : public Acts::PlanarBounds
- #include <Acts/Surfaces/EllipseBounds.hpp>
Class to describe the bounds for a planar ellispoid surface.
By providing an argument for hphisec, the bounds can be restricted to a phi-range around the center position.
Public Types
-
enum BoundValues
Values:
-
enumerator eInnerRx
-
enumerator eInnerRy
-
enumerator eOuterRx
-
enumerator eOuterRy
-
enumerator eHalfPhiSector
-
enumerator eAveragePhi
-
enumerator eSize
-
enumerator eInnerRx
Public Functions
-
EllipseBounds() = delete
-
inline EllipseBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor - from fixed size array.
- Parameters
values – The parameter values
-
inline EllipseBounds(double innerRx, double innerRy, double outerRx, double outerRy, double halfPhi = M_PI, double averagePhi = 0.) noexcept(false)
Constructor for full of an ellipsoid ring.
- Parameters
innerRx – The inner ellipse radius in x
innerRy – The inner ellipse radius in y
outerRx – The outer ellipse radius in x
outerRy – The outer ellipse radius in y
halfPhi – spanning phi sector (is set to pi as default)
averagePhi – average phi (is set to 0. as default)
-
~EllipseBounds() override = default
-
virtual const RectangleBounds &boundingBox() const final
Bounding box parameters.
- Returns
rectangle bounds for a bounding box
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck) const final
This method checks if the point given in the local coordinates is between two ellipsoids if only tol0 is given and additional in the phi sector is tol1 is given.
- Parameters
lposition – Local position (assumed to be in right surface frame)
bcheck – boundary check directive
- Returns
boolean indicator for the success of this operation
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
-
virtual BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
virtual std::vector<Vector2> vertices(unsigned int lseg) const final
Return the vertices.
Note
the number of segments to may be altered by also providing the extremas in all direction
- Parameters
lseg – the number of segments used to approximate and eventually curved line, here it refers to the full 2PI Ellipse
- Returns
vector for vertices in 2D
-
enum BoundValues
-
struct EndOfWorldReached
- #include <Acts/Propagator/StandardAborters.hpp>
This is the condition that the end of World has been reached it then triggers an propagation abort.
Public Functions
-
EndOfWorldReached() = default
boolean operator for abort condition without using the result
- Template Parameters
propagator_state_t – Type of the propagator state
navigator_t – Type of the navigator
- Parameters
state – [inout] The propagation state object
navigator – [in] The navigator object
-
EndOfWorldReached() = default
-
struct EventDataView3D
- #include <Acts/Visualization/EventDataView3D.hpp>
Public Static Functions
-
static inline std::vector<Vector3> createEllipse(double lambda0, double lambda1, double theta, size_t lseg, double offset, const Vector2 &lposition = Vector2(0., 0.), const Transform3 &transform = Transform3::Identity())
Helper method to draw the ellipse points.
- Parameters
lambda0 – The Eigenvalue in 0
lambda1 – The Eigenvalue in 1
theta – The angle between the x/y frame and EV frame
lseg – The number of segments
offset – The out of plane offset for visibility
lposition – The local anker point of the ellipse
transform – The transform to global
-
static inline std::array<double, 3> decomposeCovariance(const ActsSquareMatrix<2> &covariance)
Helper to find the eigen values and corr angle.
- Parameters
covariance – The covariance matrix
-
template<typename parameters_t>
static inline void drawBoundTrackParameters(IVisualization3D &helper, const parameters_t ¶meters, const GeometryContext &gctx = GeometryContext(), double momentumScale = 1., double locErrorScale = 1., double angularErrorScale = 1., const ViewConfig &parConfig = s_viewParameter, const ViewConfig &covConfig = s_viewParameter, const ViewConfig &surfConfig = s_viewSensitive) Helper method to draw bound parameters object.
- Parameters
helper – [in, out] The visualization helper
parameters – The bound parameters to be drawn
gctx – The geometry context for which it is drawn
momentumScale – The scale of the momentum
locErrorScale – The scale of the local error
angularErrorScale – The sclae of the angular error
parConfig – The visualization options for the parameter
covConfig – The visualization option for the covariance
surfConfig – The visualization option for the surface
-
static void drawCovarianceAngular(IVisualization3D &helper, const Vector3 &position, const Vector3 &direction, const ActsSquareMatrix<2> &covariance, double directionScale = 1, double angularErrorScale = 1, const ViewConfig &viewConfig = s_viewParameter)
Helper method to draw error cone of a direction.
- Parameters
helper – [in, out] The visualization helper
position – Where the cone originates from
direction – The direction parameters
covariance – The 2x2 covariance matrix for phi/theta
directionScale – The direction arrow length
angularErrorScale – The local Error scale
viewConfig – The visualization parameters
-
static void drawCovarianceCartesian(IVisualization3D &helper, const Vector2 &lposition, const SquareMatrix2 &covariance, const Transform3 &transform, double locErrorScale = 1, const ViewConfig &viewConfig = s_viewParameter)
Helper method to draw error ellipse.
- Parameters
helper – [in, out] The visualization helper
lposition – The local position
covariance – The covariance matrix
transform – The reference Frame transform
locErrorScale – The local Error scale
viewConfig – The visualization parameters
-
static inline void drawMeasurement(IVisualization3D &helper, const Vector2 &lposition, const SquareMatrix2 &covariance, const Transform3 &transform, const double locErrorScale = 1., const ViewConfig &measurementConfig = s_viewMeasurement)
Helper method to draw a single measurement.
TODO: Expand to 1D measurements
- Parameters
helper – [in, out] The visualization helper
lposition – calibrated measurement
covariance – calibrated covariance
transform – reference surface transformed with the geometry context
locErrorScale – The scale of the local error
measurementConfig – The visualization options for the measurement
-
template<typename traj_t>
static inline void drawMultiTrajectory(IVisualization3D &helper, const traj_t &multiTraj, const size_t &entryIndex, const GeometryContext &gctx = GeometryContext(), double momentumScale = 1., double locErrorScale = 1., double angularErrorScale = 1., const ViewConfig &surfaceConfig = s_viewSensitive, const ViewConfig &measurementConfig = s_viewMeasurement, const ViewConfig &predictedConfig = s_viewPredicted, const ViewConfig &filteredConfig = s_viewFiltered, const ViewConfig &smoothedConfig = s_viewSmoothed) Helper method to draw one trajectory stored in a MultiTrajectory object.
- Parameters
helper – [in, out] The visualization helper
multiTraj – The MultiTrajectory storing the trajectory to be drawn
entryIndex – The trajectory entry index
gctx – The geometry context for which it is drawn
momentumScale – The scale of the momentum
locErrorScale – The scale of the local error
angularErrorScale – The scale of the angular error
surfaceConfig – The visualization options for the surface
measurementConfig – The visualization options for the measurement
predictedConfig – The visualization options for the predicted measurement
filteredConfig – The visualization options for the filtered parameters
smoothedConfig – The visualization options for the smoothed parameters
-
static inline std::vector<Vector3> createEllipse(double lambda0, double lambda1, double theta, size_t lseg, double offset, const Vector2 &lposition = Vector2(0., 0.), const Transform3 &transform = Transform3::Identity())
-
struct ExaTrkXTime
- #include <Acts/Plugins/ExaTrkX/ExaTrkXTiming.hpp>
Collection of timing information of the Exa.TrkX algorithm.
Public Functions
-
inline void summary(const Logger &logger) const
Public Members
-
float building = 0.0
-
float embedding = 0.0
-
float filtering = 0.0
-
float gnn = 0.0
-
float labeling = 0.0
-
float total = 0.0
-
inline void summary(const Logger &logger) const
-
class ExaTrkXTimer
- #include <Acts/Plugins/ExaTrkX/ExaTrkXTiming.hpp>
A timer to allow easy timing.
Public Functions
-
inline ExaTrkXTimer(bool disabled = false)
-
inline double elapsed()
-
inline double elapsedSeconds()
-
inline void start()
-
inline void stop()
-
inline double stopAndGetElapsedTime()
-
inline ExaTrkXTimer(bool disabled = false)
-
class Extent
- #include <Acts/Geometry/Extent.hpp>
A class representing the geometric extent of an object in its possible dimensions, these can be all dimensions that are described as BinningValues.
The extent object can have an optional envelope in all of those values
Note
that the consistency of the different envelopes is not checked
Public Functions
-
Extent(const ExtentEnvelope &envelope = zeroEnvelopes)
Constructor with (optional)
- Parameters
envelope –
-
void addConstrain(const Extent &rhs, const ExtentEnvelope &envelope = zeroEnvelopes)
Constrain an extent by another one, this is.
values that are already constrained are not touched
values not constrained by
values that are constrained by the external one, but not by the current one, are touched
- Parameters
rhs – are not touched
envelope – an envelope applied to the constrained value
-
bool constrains(BinningValue bValue = binValues) const
Constraints check.
- Parameters
bValue – is the binning value, if all the check on all is done
-
bool contains(const Extent &rhs, BinningValue bValue = binValues) const
Contains check.
- Parameters
rhs – the extent that is check if it is contained
bValue – is the binning value, if set to binValues the check on all is done
- Returns
true if the rhs is contained
-
inline ExtentEnvelope &envelope()
Return the envelope - non-const access.
-
inline const ExtentEnvelope &envelope() const
Return the envelope - const access.
-
void extend(const Extent &rhs, const std::vector<BinningValue> &bValues = s_binningValues, bool applyEnv = true)
Extend with another geometric extent, usually pushes the current range to the boundaries of the rhs extent, unless the current extent is already bigger.
Note
the extent can also simply set an envelope which then is applied to the current one
Note
that the histogram values can not be filled in this call
- Parameters
rhs – is the other source Extent
bValues – the binning values
applyEnv – boolean to steer if envelope should be applied on the constraint values, if only an envelope is given but the value not constraint, then it is always applied
-
void extend(const Vector3 &vtx, const std::vector<BinningValue> &bValues = s_binningValues, bool applyEnv = true, bool fillHistograms = false)
Extend with a position vertex.
- Parameters
vtx – the vertex to be used for extending
bValues – the binning values
applyEnv – boolean to steer if envelope should be applied
fillHistograms – is a boolean flag to steer whether the values to fill this extent should be stored
-
template<typename vector_iterator_t>
inline void extend(const vector_iterator_t &start, const vector_iterator_t &end, const std::vector<BinningValue> &bValues = s_binningValues, bool applyEnv = true, bool fillHistograms = false) Extend with a set of vectors by iterators.
- Parameters
start – the start iterator of the loop
end – the end iterator of the loop
bValues – the binning values
applyEnv – boolean to steer if envelope should be applied
fillHistograms – is a boolean flag to steer whether the values to fill this extent should be stored
-
bool intersects(const Extent &rhs, BinningValue bValue = binValues) const
Intersection checks.
- Parameters
rhs – the extent that is check for intersection
bValue – is the binning value, if set to binValues the check on all is done
- Returns
true if the rhs intersects
-
inline ActsScalar interval(BinningValue bValue) const
Access the parameter interval (i.e.
the range span)
- Parameters
bValue – the binning identification
-
inline ActsScalar max(BinningValue bValue) const
Access the maximum parameter.
- Parameters
bValue – the binning identification
-
inline ActsScalar medium(BinningValue bValue) const
Access the midpoint.
- Parameters
bValue – the binning identification
-
inline ActsScalar min(BinningValue bValue) const
Access the minimum parameter.
- Parameters
bValue – the binning identification
-
inline bool operator!=(const Extent &e) const
Define a comparison operator.
-
bool operator==(const Extent &e) const
Define a comparison operator.
-
inline const RangeXD<binValues, ActsScalar> range() const
Return the N-dimension range.
-
inline Range1D<ActsScalar> &range(BinningValue bValue)
Return the individual 1-dimensional range.
- Parameters
bValue – is the binning value to be returned
- Returns
a one dimensional arrange
-
inline const Range1D<ActsScalar> &range(BinningValue bValue) const
Return the individual 1-dimensional range.
- Parameters
bValue – is the binning value to be returned
- Returns
a one dimensional arrange
-
template<unsigned int kSUBDIM>
inline RangeXD<kSUBDIM, ActsScalar> range(const std::array<BinningValue, kSUBDIM> &binValues) const Return an D-dimensional sub range according to the the given.
- Parameters
binValues –
-
void set(BinningValue bValue, ActsScalar min, ActsScalar max)
Set a range for a dedicated binning value.
- Parameters
bValue – the binning identification
min – the minimum parameter
max – the maximum parameter
-
void setEnvelope(const ExtentEnvelope &envelope = zeroEnvelopes)
(re-)Set the envelope
- Parameters
envelope – new envelope to be set
-
std::string toString(const std::string &indent = "") const
Convert to output stream for screen output.
- Parameters
indent – indentation for the screen display
-
inline const std::array<std::vector<ActsScalar>, binValues> &valueHistograms() const
Return the histogram store.
The histogram store can be used for automated binning detection
-
Extent(const ExtentEnvelope &envelope = zeroEnvelopes)
-
template<typename Derived, typename ...States>
class FiniteStateMachine - #include <Acts/Utilities/FiniteStateMachine.hpp>
Implementation of a finite state machine engine.
Allows setting up a system of states and transitions between them. States are definedd as empty structs (footprint: 1 byte). Transitions call functions using overload resolution. This works by subclassing this class, providing the deriving type as the first template argument (CRTP) and providing methods like
event_return on_event(const S&, const E&);
The arguments are the state
Sand the triggered eventE. Their values can be discarded (you can attach values to events of course, if you like) The return type of these functions is effectivelystd::optional<State>, so you can either returnstd::nulloptto remain in the same state, or an instance of another state. That state will then become active.You can also define a method template, which will serve as a catch-all handler (due to the fact that it will match any state/event combination):
template <typename State, typename Event> event_return on_event(const State&, const Event&) const { return Terminated{}; }
If for a given state and event no suitable overload of
on_event(and you also haven’t defined a catch-all as described above), a transition toTerminatedwill be triggered. This is essentially equivalent to the method template above.If this triggers, it will switch to the
Terminatedstate (which is always included in the FSM).Additionally, the FSM will attempt to call functions like
when entering/exiting a state. This can be used to perform actions regardless of the source or destination state in a transition to a given state. This is also fired in case a transition tovoid on_enter(const State&); void on_exit(const State&);
Terminatedoccurs.The base class also calls
during event processing, and allow for things like event and transition logging.void on_process(const Event&); void on_process(const State&, const Event&); void on_process(const State1& const Event&, const State2&);
The
on_event,on_enter,on_exitandon_processmethods need to be implemented exhaustively, i.e. for all state/event combinations. This might require you to add catch-all no-op functions likeand so on.template <typename...Args> event_return on_event(Args&&...args) {} // noop
The public interface for the user of the FSM are the
template <typename... Args> void setState(StateVariant state, Args&&... args); template <typename Event, typename... Args> void dispatch(Event&& event, Args&&... args) {
setStatetriggers a transition to a given state,dispatchtriggers processing on an event from the given state. Both will call the appropriateon_exitandon_enteroverloads. Both also accept an arbitrary number of additional arguments that are passed to theon_event,on_exitandon_enteroverloads.- Template Parameters
Derived – Class deriving from the FSM
States – Argument pack with the state types that the FSM can be handled.
Public Types
-
using StateVariant = std::variant<Terminated, States...>
Variant type allowing tagged type erased storage of the current state of the FSM.
Public Functions
-
inline FiniteStateMachine()
Default constructor.
The default state is taken to be the first in the
Statestemplate arguments
-
inline FiniteStateMachine(StateVariant state)
Constructor from an explicit state.
The FSM is initialized to this state.
- Parameters
state – Initial state for the FSM.
-
template<typename Event, typename ...Args>
inline void dispatch(Event &&event, Args&&... args) Public interface to handle an event.
Will call the appropriate event handlers and perform any required transitions.
- Template Parameters
Event – Type of the event being triggered
Args – Additional arguments being passed to overload handlers.
- Parameters
event – Instance of the event being triggere
args – Additional arguments
-
inline const StateVariant &getState() const noexcept
Get the current state of the FSM (as a variant).
- Returns
StateVariant The current state of the FSM.
-
template<typename S>
inline bool is() const noexcept Returns whether the FSM is in the specified state.
Alternative version directly taking only the template argument.
- Template Parameters
State – type to check against
- Returns
Whether the FSM is in the given state.
-
template<typename S>
inline bool is(const S &state) const noexcept Returns whether the FSM is in the specified state.
- Template Parameters
State – type to check against
- Parameters
state – State instance to check against
- Returns
Whether the FSM is in the given state.
-
template<typename State, typename ...Args>
inline void setState(State state, Args&&... args) Sets the state to a given one.
Triggers
on_exitandon_enterfor the given states.- Template Parameters
State – Type of the target state
Args – Additional arguments passed through callback overloads.
- Parameters
state – Instance of the target state
args – The additional arguments
-
inline bool terminated() const noexcept
Returns whether the FSM is in the terminated state.
- Returns
Whether the FSM is in the terminated state.
-
struct Terminated
- #include <Acts/Utilities/FiniteStateMachine.hpp>
Contractual termination state.
Is transitioned to if State+Event do not have a transition defined.
Public Static Attributes
-
static constexpr std::string_view name = "Terminated"
Name of this state (useful for logging)
-
static constexpr std::string_view name = "Terminated"
-
template<typename value_t, size_t DIM, size_t SIDES>
class Frustum - #include <Acts/Utilities/Frustum.hpp>
Class representing a frustum shape.
The frustum is defined using an origin, a direction and an opening angle. These parameters are then used to calculate a number of side planes, each having a position and a normal vector. The “near plane” is assumed to coincide with the origin point, and the normal with the “direction” of the frustum. No far plane is defined.
- Template Parameters
value_t – The floating point value to use
DIM – The number of dimensions of ambient space
SIDES – The number of sides (= side planes) the frustum has (exactly 2 in 2D, minimum 3 in 3D)
Public Types
-
using value_type = value_t
Re expose the value type.
Public Functions
-
template<size_t D = DIM, std::enable_if_t<D == 2, int> = 0>
Frustum(const VertexType &origin, const VertexType &dir, value_type opening_angle) Constructor for the 2D case.
Note
The
opening_angleis defined as the angle between opposing side planes. The opening angle needs to be < pi.- Parameters
origin – The origin of the frustum
dir – The direction of the frustum
opening_angle – The opening angle
-
template<size_t D = DIM, std::enable_if_t<D == 3, int> = 0>
Frustum(const VertexType &origin, const VertexType &dir, value_type opening_angle) Constructor for the 3D case.
Note
The
opening_angleis defined as the angle between opposing side planes. The opening angle needs to be < pi.- Parameters
origin – The origin of the frustum
dir – The direction of the frustum
opening_angle – The opening angle
-
inline const VertexType &dir() const
Getter for the direction of the frustum.
- Returns
The direction of the frustum
-
template<size_t D = DIM, std::enable_if_t<D == 3, int> = 0>
void draw(IVisualization3D &helper, value_type far_distance = 10) const Draw a representation of this frustum using a visualization helper.
Note
This is only available for the 3D case.
- Parameters
helper – The visualization helper
far_distance – The distance to the virtual “far plane” at which point the side planes terminate visually.
-
inline const std::array<VertexType, SIDES + 1> &normals() const
Getter for the normal vectors of the planes defining this frustum.
Note
The size of the array that is returned is fixed to
number of sides + 1- Returns
Array containing the normal vectors for all planes.
-
inline const VertexType &origin() const
Getter for the oriogin of the frustum.
- Returns
The origin of the frustum
-
template<size_t D = DIM, std::enable_if_t<D == 2, int> = 0>
std::ostream &svg(std::ostream &os, value_type w, value_type h, value_type far_distance = 1, value_type unit = 20.) const Draw a representation of this frustum as an SVG string to an outstream.
Note
This is only available for the 2D case.
- Parameters
os – The out stream to write to
w – The width of the output SVG
h – The height of the output SVG
far_distance – The distance to the virtual “far line” at which point the side lines terminate visually.
unit – Multiplicative factor to apply to internal distances
-
Frustum<value_t, DIM, SIDES> transformed(const transform_type &trf) const
Transforms this frustum using a given transform and returns a new instance.
- Parameters
trf – The transform to apply
- Returns
A copy of this frustum with the transform
trfapplied.
-
class FsmwMode1dFinder
- #include <Acts/Vertexing/FsmwMode1dFinder.hpp>
Calculates the mode of a unidimenensional distribution using the Fraction of Sample Mode with Weights algorithm For reference, see: On a Fast, Robust Estimator of the Mode: Comparisons to Other Robust Estimators with Applications, David R.
Bickel, Rudolf Fruehwirth, arXiv:math/0505419 It’s like an iterative “Half Sample Mode”, but the fraction you take at each step can be configured by the user. Configuration possibilities: (1) fraction (default is 50 %) (2) firstFraction (default is 50 %)
Public Functions
-
FsmwMode1dFinder() = default
Default constructor.
-
FsmwMode1dFinder(double firstFraction, double fraction)
Overload constructor.
- Parameters
firstFraction – first fraction in FSMW algorithm
fraction – all other fractions in FSMW algorithm
-
Result<double> getMode(std::vector<std::pair<double, double>> inputVector) const
Function to calculate mode with FSMW algorithm.
- Parameters
inputVector – Input collection to calculate mode from
- Returns
mode value
-
FsmwMode1dFinder() = default
-
template<typename input_track_t, typename linearizer_t>
class FullBilloirVertexFitter - #include <Acts/Vertexing/FullBilloirVertexFitter.hpp>
Vertex fitter class implementing the Billoir vertex fitter.
This class implements the Billoir vertex fitter from Ref. (1). It is also useful to have a look at Ref. (2). Note that the Billoir vertex fitter outputs one 4D vertex position and nTrack momenta at this very point.
Ref. (1): Fast vertex fitting with a local parametrization of tracks. Author(s) Billoir, P ; Qian, S In: Nucl. Instrum. Methods Phys. Res., A 311 (1992) 139-150 DOI 10.1016/0168-9002(92)90859-3
Ref. (2): Pattern Recognition, Tracking and Vertex Reconstruction in Particle Detectors. Author(s) Fruehwirth, R ; Strandli, A
- Template Parameters
input_track_t – Track object type
linearizer_t – Track linearizer type
Public Types
-
using InputTrack_t = input_track_t
-
using Linearizer_t = linearizer_t
-
using Propagator_t = typename linearizer_t::Propagator_t
Public Functions
-
template<typename T = input_track_t, std::enable_if_t<std::is_same<T, BoundTrackParameters>::value, int> = 0>
inline FullBilloirVertexFitter(const Config &cfg) Constructor used if input_track_t type == BoundTrackParameters.
- Parameters
cfg – Configuration object
-
inline FullBilloirVertexFitter(const Config &cfg, std::function<BoundTrackParameters(input_track_t)> func)
Constructor for user-defined input_track_t type =! BoundTrackParameters.
- Parameters
cfg – Configuration object
func – Function extracting BoundTrackParameters from input_track_t object
-
Result<Vertex<input_track_t>> fit(const std::vector<const input_track_t*> ¶mVector, const linearizer_t &linearizer, const VertexingOptions<input_track_t> &vertexingOptions, State &state) const
Fit method, fitting vertex for provided tracks with constraint.
- Parameters
paramVector – Vector of track objects to fit vertex to
linearizer – The track linearizer
vertexingOptions – Vertexing options
state – The state object
- Returns
Fitted vertex
-
struct Config
- #include <Acts/Vertexing/FullBilloirVertexFitter.hpp>
Public Members
-
int maxIterations = 5
Maximum number of iterations in fitter.
-
int maxIterations = 5
-
struct State
- #include <Acts/Vertexing/FullBilloirVertexFitter.hpp>
Public Functions
-
inline State(MagneticFieldProvider::Cache fieldCache)
The state constructor.
- Parameters
fieldCache – The magnetic field cache
Public Members
-
Linearizer_t::State linearizerState
The linearizer state.
-
inline State(MagneticFieldProvider::Cache fieldCache)
-
class GainMatrixSmoother
- #include <Acts/TrackFitting/GainMatrixSmoother.hpp>
Kalman trajectory smoother based on gain matrix formalism.
This implements not a single smoothing step, but the full backwards smoothing procedure for a filtered, forward trajectory using the stored linearization.
Public Types
-
using GetCovariance = Acts::Delegate<TrackStateTraits<MultiTrajectoryTraits::MeasurementSizeMax, false>::Covariance(void*)>
-
using GetParameters = Acts::Delegate<TrackStateTraits<MultiTrajectoryTraits::MeasurementSizeMax, false>::Parameters(void*)>
Public Functions
-
Result<void> calculate(void *ts, void *prev_ts, const GetParameters &filtered, const GetCovariance &filteredCovariance, const GetParameters &smoothed, const GetParameters &predicted, const GetCovariance &predictedCovariance, const GetCovariance &smoothedCovariance, const GetCovariance &jacobian, const Logger &logger) const
-
template<typename traj_t>
inline Result<void> operator()(const GeometryContext &gctx, traj_t &trajectory, size_t entryIndex, const Logger &logger = getDummyLogger()) const Run the Kalman smoothing for one trajectory.
- Parameters
gctx – [in] The geometry context for the smoothing
trajectory – [inout] The trajectory to be smoothed
entryIndex – [in] The index of state to start the smoothing
logger – [in] Where to write logging information to
-
using GetCovariance = Acts::Delegate<TrackStateTraits<MultiTrajectoryTraits::MeasurementSizeMax, false>::Covariance(void*)>
-
class GainMatrixUpdater
- #include <Acts/TrackFitting/GainMatrixUpdater.hpp>
Kalman update step using the gain matrix formalism.
Public Functions
-
template<typename traj_t>
inline Result<void> operator()(const GeometryContext &gctx, typename traj_t::TrackStateProxy trackState, Direction direction = Direction::Forward, const Logger &logger = getDummyLogger()) const Run the Kalman update step for a single trajectory state.
- Template Parameters
kMeasurementSizeMax –
- Parameters
gctx – [in] The current geometry context object, e.g. alignment
trackState – [inout] The track state
direction – [in] The navigation direction
logger – [in] Where to write logging information to
-
template<typename traj_t>
-
template<int mainGridSize = 2000, int trkGridSize = 15>
class GaussianGridTrackDensity - #include <Acts/Vertexing/GaussianGridTrackDensity.hpp>
Implements a 1-dim density grid to be filled with track Gaussian distributions.
Each single track is modelled as a 2(!)-dim Gaussian distribution grid in the d0-z0 plane, but only the overlap with the z-axis (i.e. a 1-dim density vector) needs to be calculated. The position of the highest track density (of either a single bin or the sum of a certain region) can be determined. Single tracks can be cached and removed from the overall density.
- Template Parameters
mainGridSize – The size of the z-axis 1-dim main density grid
trkGridSize – The 2(!)-dim grid size of a single track, i.e. a single track is modelled as a (trkGridSize x trkGridSize) grid in the d0-z0 plane. Note: trkGridSize has to be an odd value.
Public Types
-
using MainGridVector = Eigen::Matrix<float, mainGridSize, 1>
-
using TrackGridVector = Eigen::Matrix<float, trkGridSize, 1>
Public Functions
-
inline GaussianGridTrackDensity(const Config &cfg)
-
std::pair<int, TrackGridVector> addTrack(const BoundTrackParameters &trk, MainGridVector &mainGrid) const
Adds a single track to the overall grid density.
- Parameters
trk – The track to be added
mainGrid – The main 1-dim density grid along the z-axis
- Returns
A pair storing information about the z-bin position the track was added (int) and the 1-dim density contribution of the track itself
-
Result<float> getMaxZPosition(MainGridVector &mainGrid) const
Returns the z position of maximum track density.
- Parameters
mainGrid – The main 1-dim density grid along the z-axis
- Returns
The z position of maximum track density
-
Result<std::pair<float, float>> getMaxZPositionAndWidth(MainGridVector &mainGrid) const
Returns the z position of maximum track density and the estimated width.
- Parameters
mainGrid – The main 1-dim density grid along the z-axis
- Returns
The z position of maximum track density and width
-
void removeTrackGridFromMainGrid(int zBin, const TrackGridVector &trkGrid, MainGridVector &mainGrid) const
Removes a track from the overall grid density.
- Parameters
zBin – The center z-bin position the track needs to be removed from
trkGrid – The 1-dim density contribution of the track
mainGrid – The main 1-dim density grid along the z-axis
-
struct Config
- #include <Acts/Vertexing/GaussianGridTrackDensity.hpp>
The configuration struct.
Public Functions
-
inline Config(float zMinMax_ = 100)
Note
The value of
zMinMax_together withmainGridSizedetermines the overall bin size to be used as seen below- Parameters
zMinMax_ – The minimum and maximum z-values (in mm) that should be covered by the main 1-dim density grid along the z-axis
Public Members
-
float binSize
-
float maxRelativeDensityDev = 0.01
-
bool useHighestSumZPosition = false
-
float zMinMax
-
inline Config(float zMinMax_ = 100)
-
template<typename input_track_t>
class GaussianTrackDensity - #include <Acts/Vertexing/GaussianTrackDensity.hpp>
Class to model tracks as 2D density functions based on their d0 and z0 perigee parameters (mean value) and covariance matrices (determining the width of the function)
Public Functions
-
GaussianTrackDensity() = default
Default constructor.
-
inline GaussianTrackDensity(const Config &cfg)
Constructor with config.
-
double globalMaximum(State &state, const std::vector<const input_track_t*> &trackList, const std::function<BoundTrackParameters(input_track_t)> &extractParameters) const
Calculates the z position of the global maximum.
- Parameters
state – The track density state
trackList – All input tracks
extractParameters – Function extracting BoundTrackParameters from InputTrack
- Returns
z position of the global maximum
-
std::pair<double, double> globalMaximumWithWidth(State &state, const std::vector<const input_track_t*> &trackList, const std::function<BoundTrackParameters(input_track_t)> &extractParameters) const
Calculates z position of global maximum with Gaussian width for density function.
Strategy: The global maximum must be somewhere near a track. Since we can calculate the first and second derivatives, at each point we can determine a) whether the function is curved up (minimum) or down (maximum) b) the distance to nearest maximum, assuming either Newton (parabolic) or Gaussian local behavior. For each track where the second derivative is negative, find step to nearest maximum, take that step and then do one final refinement. The largest density encountered in this procedure (after checking all tracks) is considered the maximum.
- Parameters
state – The track density state
trackList – All input tracks
extractParameters – Function extracting BoundTrackParameters from InputTrack
- Returns
Pair of position of global maximum and Gaussian width
-
struct Config
- #include <Acts/Vertexing/GaussianTrackDensity.hpp>
The Config struct.
Public Functions
-
inline Config(double d0Sig = 3.5, double z0Sig = 12.)
Public Members
-
double d0MaxSignificance
-
double d0SignificanceCut
-
bool isGaussianShaped = true
-
double z0MaxSignificance
-
double z0SignificanceCut
-
inline Config(double d0Sig = 3.5, double z0Sig = 12.)
-
struct State
- #include <Acts/Vertexing/GaussianTrackDensity.hpp>
The State struct.
Public Functions
-
inline State(unsigned int nTracks)
Public Members
-
std::vector<TrackEntry> trackEntries
-
inline State(unsigned int nTracks)
-
struct TrackEntry
- #include <Acts/Vertexing/GaussianTrackDensity.hpp>
Struct to store information for a single track.
Public Functions
-
TrackEntry() = default
Default constructor.
-
inline TrackEntry(double z_, double c0_, double c1_, double c2_, double lowerBound_, double upperBound_)
Constructor initializing all members.
- Parameters
z_ – Trial z position
c0_ – z-independent term in exponent
c1_ – Linear coefficient in exponent
c2_ – Quadratic coefficient in exponent
lowerBound_ – The lower bound
upperBound_ – The upper bound
Public Members
-
double c0 = 0
-
double c1 = 0
-
double c2 = 0
-
double lowerBound = 0
-
double upperBound = 0
-
double z = 0
-
TrackEntry() = default
-
GaussianTrackDensity() = default
-
class GenericApproachDescriptor : public Acts::ApproachDescriptor
- #include <Acts/Geometry/GenericApproachDescriptor.hpp>
Class to decide and return which approaching surface to be taken, it’s a generic descriptor for n surfaces.
It is templated in order to allow for BoundarySurfaces from representing volumes of layers to be re-used
Public Functions
A generic approach descriptor for new Acts::Surface objects passing ownership.
- Parameters
aSurfaces – are the approach surfaces
-
~GenericApproachDescriptor() override = default
A generic approach descriptor with n surfaces to test.
-
virtual ObjectIntersection<Surface> approachSurface(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck) const override
Get the approach surface to the layer.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The global position to start the approach from
direction – The momentum vector
bcheck – The boundary check prescription
- Returns
: a SurfaceIntersection
-
virtual const std::vector<const Surface*> &containedSurfaces() const override
return all contained surfaces of this approach descriptor
-
virtual std::vector<const Surface*> &containedSurfaces() override
Non-const version.
-
virtual void registerLayer(const Layer &lay) override
Register the Layer to the surfaces.
- Parameters
lay – is the layer to be registered
-
template<class charge_t>
class GenericBoundTrackParameters - #include <Acts/EventData/GenericBoundTrackParameters.hpp>
Track parameters bound to a reference surface for a single track.
This is intended as a user-facing data class that adds additional accessors and charge/momentum interpretation on top of the pure parameters vector. All parameters and their corresponding covariance matrix are stored in bound parametrization. The specific definition of the local spatial parameters is defined by the associated surface.
Note
This class holds shared ownership on its reference surface.
- Template Parameters
charge_t – Helper type to interpret the particle charge/momentum
Subclassed by Acts::GenericCurvilinearTrackParameters< charge_t >
Public Types
-
using CovarianceMatrix = BoundSquareMatrix
-
using ParametersVector = BoundVector
-
using Scalar = ActsScalar
Public Functions
-
GenericBoundTrackParameters() = delete
Parameters are not default constructible due to the charge type.
-
GenericBoundTrackParameters(const GenericBoundTrackParameters&) = default
-
GenericBoundTrackParameters(GenericBoundTrackParameters&&) = default
Construct from a parameters vector on the surface and particle charge.
In principle, only the charge magnitude is needed her to allow unambiguous extraction of the absolute momentum. The particle charge is required as an input here to be consistent with the other constructors below that that also take the charge as an input. The charge sign is only used in debug builds to check for consistency with the q/p parameter.
- Parameters
surface – Reference surface the parameters are defined on
params – Bound parameters vector
q – Particle charge
cov – Bound parameters covariance matrix
Construct from a parameters vector on the surface.
This constructor is only available if there are no potential charge ambiguities, i.e. the charge type is default-constructible.
- Parameters
surface – Reference surface the parameters are defined on
params – Bound parameters vector
cov – Bound parameters covariance matrix
-
~GenericBoundTrackParameters() = default
-
inline Scalar absoluteMomentum() const
Absolute momentum.
-
inline Scalar charge() const
Particle electric charge.
-
inline std::optional<CovarianceMatrix> &covariance()
Optional covariance matrix.
-
inline const std::optional<CovarianceMatrix> &covariance() const
Optional covariance matrix.
-
inline Vector3 direction() const
Unit direction three-vector, i.e.
the normalized momentum three-vector.
-
inline Vector4 fourPosition(const GeometryContext &geoCtx) const
Space-time position four-vector.
This uses the associated surface to transform the local position on the surface to globalcoordinates. This requires a geometry context to select the appropriate transformation and might be a computationally expensive operation.
- Parameters
geoCtx – [in] Geometry context for the local-to-global transformation
-
template<BoundIndices kIndex>
inline Scalar get() const Access a single parameter value identified by its index.
- Template Parameters
kIndex – Track parameter index
-
inline Vector2 localPosition() const
Local spatial position two-vector.
-
inline Vector3 momentum() const
Momentum three-vector.
-
GenericBoundTrackParameters &operator=(const GenericBoundTrackParameters&) = default
-
GenericBoundTrackParameters &operator=(GenericBoundTrackParameters&&) = default
-
inline ParametersVector ¶meters()
Parameters vector.
-
inline const ParametersVector ¶meters() const
Parameters vector.
-
inline Scalar phi() const
Phi direction.
-
inline Vector3 position(const GeometryContext &geoCtx) const
Spatial position three-vector.
This uses the associated surface to transform the local position on the surface to globalcoordinates. This requires a geometry context to select the appropriate transformation and might be a computationally expensive operation.
- Parameters
geoCtx – [in] Geometry context for the local-to-global transformation
-
inline Scalar qOverP() const
Charge over momentum.
-
inline RotationMatrix3 referenceFrame(const GeometryContext &geoCtx) const
Reference frame in which the local error is defined.
For planar surfaces, this is the transformation local-to-global rotation matrix. For non-planar surfaces, it is the local-to-global rotation matrix of the tangential plane at the track position.
- Parameters
geoCtx – [in] Geometry context for the local-to-global transformation
-
inline const Surface &referenceSurface() const
Reference surface onto which the parameters are bound.
-
inline Scalar theta() const
Theta direction.
-
inline Scalar time() const
Time coordinate.
-
inline Scalar transverseMomentum() const
Transverse momentum.
Public Static Functions
Factory to construct from four-position, direction, absolute momentum, and charge.
Note
The returned result indicates whether the free parameters could successfully be converted to on-surface parameters.
- Parameters
surface – Reference surface the parameters are defined on
geoCtx – Geometry context for the local-to-global transformation
pos4 – Track position/time four-vector
dir – Track direction three-vector; normalization is ignored.
p – Absolute momentum
q – Particle charge
cov – Bound parameters covariance matrix
Factory to construct from four-position, direction, and charge-over-momentum.
Note
This factory is only available if there are no potential charge ambiguities, i.e. the charge type is default-constructible. The position must be located on the surface.
Note
The returned result indicates whether the free parameters could successfully be converted to on-surface parameters.
- Parameters
surface – Reference surface the parameters are defined on
geoCtx – Geometry context for the local-to-global transformation
pos4 – Track position/time four-vector
dir – Track direction three-vector; normalization is ignored.
qOverP – Charge-over-momentum-like parameter
cov – Bound parameters covariance matrix
-
class GenericCuboidVolumeBounds : public Acts::VolumeBounds
- #include <Acts/Geometry/GenericCuboidVolumeBounds.hpp>
Public Functions
-
GenericCuboidVolumeBounds() = delete
-
GenericCuboidVolumeBounds(const std::array<Acts::Vector3, 8> &vertices) noexcept(false)
Constructor from a set of vertices.
The ordering is considered to be:
the first 4 vertices are the “top” face
the second 4 vertices are the “bottom” face
both faces are given in counter clock wise order
- Parameters
vertices – The set of input vertices
-
GenericCuboidVolumeBounds(const std::array<double, BoundValues::eSize> &values) noexcept(false)
Constructor from a fixed size array.
- Parameters
values – The input values
-
~GenericCuboidVolumeBounds() override = default
-
virtual Volume::BoundingBox boundingBox(const Transform3 *trf = nullptr, const Vector3 &envelope = {0, 0, 0}, const Volume *entity = nullptr) const final
Construct bounding box for this shape.
- Parameters
trf – Optional transform
envelope – Optional envelope to add / subtract from min/max
entity – Entity to associate this bounding box with
- Returns
Constructed bounding box
-
void draw(IVisualization3D &helper, const Transform3 &transform = Transform3::Identity()) const
Draw this shape using a visualization helper.
- Parameters
helper – The visualizatin helper
transform – Optional transformation matrix
-
virtual bool inside(const Vector3 &gpos, double tol = 0.) const override
Checking if position given in volume frame is inside.
- Parameters
gpos – is the global position to be checked
tol – is the tolerance applied for the inside check
- Returns
boolean indicating if the position is inside
-
virtual OrientedSurfaces orientedSurfaces(const Transform3 &transform = Transform3::Identity()) const override
Oriented surfaces, i.e.
the decomposed boundary surfaces and the according navigation direction into the volume given the normal vector on the surface
It will throw an exception if the orientation prescription is not adequate
- Parameters
transform – is the 3D transform to be applied to the boundary surfaces to position them in 3D space
- Returns
a vector of surfaces bounding this volume
-
virtual std::ostream &toStream(std::ostream &sl) const override
- Parameters
sl – is the output stream to be written into
-
inline virtual VolumeBounds::BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
struct BoundValues
- #include <Acts/Geometry/GenericCuboidVolumeBounds.hpp>
This struct helps to symmetrize with the the other volume bounds classes.
Public Static Attributes
-
static constexpr size_t eSize = 24
-
static constexpr size_t eSize = 24
-
GenericCuboidVolumeBounds() = delete
-
template<typename charge_t>
class GenericCurvilinearTrackParameters : public Acts::GenericBoundTrackParameters<charge_t> - #include <Acts/EventData/GenericCurvilinearTrackParameters.hpp>
Curvilinear track parameters for a single track.
This is intended as a user-facing data class that adds additional accessors and charge/momentum interpretation on top of the pure parameters vector. All parameters and their corresponding covariance matrix are stored in curvilinear parametrization.
See also
GenericBoundTrackParameters
- Template Parameters
charge_t – Helper type to interpret the particle charge/momentum
Public Types
-
using CovarianceMatrix = BoundSquareMatrix
-
using ParametersVector = BoundVector
-
using Scalar = ActsScalar
Public Functions
-
GenericCurvilinearTrackParameters() = delete
Parameters are not default constructible due to the charge type.
-
GenericCurvilinearTrackParameters(const GenericCurvilinearTrackParameters&) = default
-
inline GenericCurvilinearTrackParameters(const Vector4 &pos4, const Vector3 &dir, Scalar p, Scalar q, std::optional<CovarianceMatrix> cov = std::nullopt)
Construct from four-position, direction, absolute momentum, and charge.
- Parameters
pos4 – Track position/time four-vector
dir – Track direction three-vector; normalization is ignored.
p – Absolute momentum
q – Particle charge
cov – Curvilinear bound parameters covariance matrix
-
template<typename T = charge_t, std::enable_if_t<std::is_default_constructible_v<T>, int> = 0>
inline GenericCurvilinearTrackParameters(const Vector4 &pos4, const Vector3 &dir, Scalar qOverP, std::optional<CovarianceMatrix> cov = std::nullopt) Construct from four-position, direction, and charge-over-momentum.
This constructor is only available if there are no potential charge ambiguities, i.e. the charge interpretation type is default-constructible.
- Parameters
pos4 – Track position/time four-vector
dir – Track direction three-vector; normalization is ignored.
qOverP – Charge-over-momentum-like parameter
cov – Curvilinear bound parameters covariance matrix
-
inline GenericCurvilinearTrackParameters(const Vector4 &pos4, Scalar phi, Scalar theta, Scalar p, Scalar q, std::optional<CovarianceMatrix> cov = std::nullopt)
Construct from four-position, angles, absolute momentum, and charge.
- Parameters
pos4 – Track position/time four-vector
phi – Transverse track direction angle
theta – Longitudinal track direction angle
p – Absolute momentum
q – Particle charge
cov – Curvilinear bound parameters covariance matrix
-
template<typename T = charge_t, std::enable_if_t<std::is_default_constructible_v<T>, int> = 0>
inline GenericCurvilinearTrackParameters(const Vector4 &pos4, Scalar phi, Scalar theta, Scalar qOverP, std::optional<CovarianceMatrix> cov = std::nullopt) Construct from four-position, angles, and charge-over-momentum.
This constructor is only available if there are no potential charge ambiguities, i.e. the charge interpretation type is default-constructible.
- Parameters
pos4 – Track position/time four-vector
phi – Transverse track direction angle
theta – Longitudinal track direction angle
qOverP – Charge-over-momentum-like parameter
cov – Curvilinear bound parameters covariance matrix
-
GenericCurvilinearTrackParameters(GenericCurvilinearTrackParameters&&) = default
-
~GenericCurvilinearTrackParameters() = default
-
inline Vector4 fourPosition() const
Space-time position four-vector.
-
GenericCurvilinearTrackParameters &operator=(const GenericCurvilinearTrackParameters&) = default
-
GenericCurvilinearTrackParameters &operator=(GenericCurvilinearTrackParameters&&) = default
-
inline Vector3 position() const
Spatial position three-vector.
-
template<class charge_t>
class GenericFreeTrackParameters - #include <Acts/EventData/GenericFreeTrackParameters.hpp>
Track parameters not bound to a surface for a single track.
Parameters and covariance matrix are stored using the free parametrization defined in
enum FreeIndices.- Template Parameters
charge_t – Helper type to interpret the particle charge
Public Types
-
using CovarianceMatrix = FreeSquareMatrix
-
using ParametersVector = FreeVector
-
using Scalar = ActsScalar
Public Functions
-
GenericFreeTrackParameters() = delete
Parameters are not default constructible due to the charge type.
-
GenericFreeTrackParameters(const GenericFreeTrackParameters&) = default
-
inline GenericFreeTrackParameters(const ParametersVector ¶ms, Scalar q, std::optional<CovarianceMatrix> cov = std::nullopt)
Construct from a parameters vector and particle charge.
In principle, only the charge magnitude is needed her to allow unambiguous extraction of the absolute momentum. The particle charge is required as an input here to be consistent with the other constructors below that that also take the charge as an input. The charge sign is only used in debug builds to check for consistency with the q/p parameter.
- Parameters
params – Free parameters vector
q – Particle charge
cov – Free parameters covariance matrix
-
template<typename T = charge_t, std::enable_if_t<std::is_default_constructible_v<T>, int> = 0>
inline GenericFreeTrackParameters(const ParametersVector ¶ms, std::optional<CovarianceMatrix> cov = std::nullopt) Construct from a parameters vector.
This constructor is only available if there are no potential charge ambiguities, i.e. the charge interpretation type is default-constructible.
- Parameters
params – Free parameters vector
cov – Free parameters covariance matrix
- Template Parameters
T – Internal helper template be able to check charge type
-
inline GenericFreeTrackParameters(const Vector4 &pos4, Scalar phi, Scalar theta, Scalar p, Scalar q, std::optional<CovarianceMatrix> cov = std::nullopt)
Construct from four-position, angles, absolute momentum, and charge.
- Parameters
pos4 – Track position/time four-vector
phi – Transverse track direction angle
theta – Longitudinal track direction angle
p – Absolute momentum
q – Particle charge
cov – Free parameters covariance matrix
-
template<typename T = charge_t, std::enable_if_t<std::is_default_constructible_v<T>, int> = 0>
inline GenericFreeTrackParameters(const Vector4 &pos4, Scalar phi, Scalar theta, Scalar qOverP, std::optional<CovarianceMatrix> cov = std::nullopt) Construct from four-position, angles, and charge-over-momentum.
This constructor is only available if there are no potential charge ambiguities, i.e. the charge interpretation type is default-constructible.
- Parameters
pos4 – Track position/time four-vector
phi – Transverse track direction angle
theta – Longitudinal track direction angle
qOverP – Charge-over-momentum-like parameter
cov – Free parameters covariance matrix
-
GenericFreeTrackParameters(GenericFreeTrackParameters&&) = default
-
~GenericFreeTrackParameters() = default
-
inline Scalar absoluteMomentum() const
Absolute momentum.
-
inline Scalar charge() const
Particle electric charge.
-
inline const std::optional<CovarianceMatrix> &covariance() const
Optional covariance matrix.
-
inline Vector3 direction() const
Unit direction three-vector, i.e. the normalized momentum three-vector.
-
inline Vector4 fourPosition() const
Space-time position four-vector.
-
template<FreeIndices kIndex>
inline Scalar get() const Access a single parameter value identified by its index.
- Template Parameters
kIndex – Track parameter index
-
inline Vector3 momentum() const
Momentum three-vector.
-
GenericFreeTrackParameters &operator=(const GenericFreeTrackParameters&) = default
-
GenericFreeTrackParameters &operator=(GenericFreeTrackParameters&&) = default
-
inline const ParametersVector ¶meters() const
Parameters vector.
-
inline Scalar phi() const
Phi direction.
-
inline Vector3 position() const
Spatial position three-vector.
-
inline Scalar qOverP() const
Charge over momentum.
-
inline Scalar theta() const
Theta direction.
-
inline Scalar time() const
Time coordinate.
-
inline Scalar transverseMomentum() const
Transverse momentum.
-
template<ACTS_CONCEPT charge_t(ChargeConcept)>
class GenericParticleHypothesis - #include <Acts/EventData/GenericParticleHypothesis.hpp>
Particle hypothesis used in reconstruction.
The reconstruction hypothesis consists of absolute PDG code, mass and absolute charge.
Public Types
-
using ChargeType = charge_t
Public Functions
-
template<typename other_charge_t>
inline constexpr GenericParticleHypothesis(const GenericParticleHypothesis<other_charge_t> &other) Copy from another charge hypothesis.
Note
This enables implicit conversion.
-
inline GenericParticleHypothesis(PdgParticle absPdg)
Creates a particle hypothesis using the absolute PDG.
The mass and charge is looked up using findMass and findCharge. If the lookup fails an exception is thrown.
- Parameters
absPdg – the absolute PDG
-
inline constexpr GenericParticleHypothesis(PdgParticle absPdg, float mass, ChargeType chargeType)
Creates a particle hypothesis using absolute PDG, mass and the charge type.
- Parameters
absPdg – the absolute PDG
mass – the particle mass
chargeType – the type of charge
-
inline constexpr float absoluteCharge() const noexcept
Get the hypothesized absolute charge.
-
inline constexpr PdgParticle absolutePdg() const noexcept
Get the hypothesized absolute PDG.
-
inline constexpr const ChargeType &chargeType() const noexcept
Get the hypothesized charge type.
-
template<typename T>
inline constexpr auto extractCharge(T qOverP) const noexcept Extracts the signed charge from the
q over ptrack parameter using the charge hypothesis.- Parameters
qOverP – the
q over ptrack parameter.
-
template<typename T>
inline constexpr auto extractMomentum(T qOverP) const noexcept Extracts the signed charge from the
q over ptrack parameter using the charge hypothesis.- Parameters
qOverP – the
q over ptrack parameter.
-
inline constexpr float mass() const noexcept
Get the hypothesized mass.
-
using ChargeType = charge_t
-
template<typename value_t>
class GeometryHierarchyMap - #include <Acts/Geometry/GeometryHierarchyMap.hpp>
Store values mapped into the geometry hierarchy.
The core functionality is to find an equivalent element, i.e. an identifier-value pair, for a given geometry identifier via
Trailing zero levels of stored geometry identifiers are used as broadcast values to refer to higher-level objects within the geometry, e.g. a geometry identifier with vanishing approach and sensitive index identifies a layer. An entry will all geometry identifier levels set to zero acts as the global default value.auto it = container.find(GeometryIdentifier(...)); if (it != container.end()) { ... }
The container also supports range-based iteration over all stored elements
and index-based access to stored elements and associated geometry identifiersfor (const auto& element : container) { ... }
Adding elements is potentially expensive as the internal lookup structure must be updated. In addition, modifying an element in-place could change its identifier which would also break the lookup. Thus, the container can not be modified after construction to prevent misuse.GeometryIdentifier id3 = container.idAt(3); const auto& element4 = container.valueAt(4);
Note
No guarantees are given for the element order when using range-based or index-based access. Any apparent ordering must be considered an implementation detail and might change.
- Template Parameters
value_t – stored value type
Public Types
-
using InputElement = typename std::pair<GeometryIdentifier, value_t>
Combined geometry identifier and value element. Only used for input.
-
using Iterator = typename std::vector<value_t>::const_iterator
-
using Size = typename std::vector<value_t>::size_type
-
using Value = value_t
Public Functions
-
GeometryHierarchyMap() = default
-
GeometryHierarchyMap(const GeometryHierarchyMap&) = default
-
GeometryHierarchyMap(GeometryHierarchyMap&&) = default
-
inline GeometryHierarchyMap(std::initializer_list<InputElement> elements)
Construct the container from an initializer list.
- Parameters
elements – input initializer list
-
inline GeometryHierarchyMap(std::vector<InputElement> elements)
Construct the container from the given elements.
- Parameters
elements – input elements (must be unique with respect to identifier)
-
~GeometryHierarchyMap() = default
-
inline Iterator begin() const
Return an iterator pointing to the beginning of the stored values.
-
inline bool empty() const
Check if any elements are stored.
-
inline Iterator end() const
Return an iterator pointing to the end of the stored values.
-
inline Iterator find(GeometryIdentifier id) const
Find the most specific value for a given geometry identifier.
This can be either from the element matching exactly to the given geometry id, if it exists, or from the element for the next available higher level within the geometry hierarchy.
- Parameters
id – geometry identifier for which information is requested
- Return values
iterator – to an existing value
<tt>.end()</tt> – iterator if no matching element exists
-
inline GeometryIdentifier idAt(Size index) const
Access the geometry identifier for the i-th element with bounds check.
- Throws
std::out_of_range – for invalid indices
-
GeometryHierarchyMap &operator=(const GeometryHierarchyMap&) = default
-
GeometryHierarchyMap &operator=(GeometryHierarchyMap&&) = default
-
inline Size size() const
Return the number of stored elements.
-
template<typename value_t, class decorator_t = void>
class GeometryHierarchyMapJsonConverter - #include <Acts/Plugins/Json/GeometryHierarchyMapJsonConverter.hpp>
Convert a geometry hierarchy map to/from Json.
The value type is expected to be directly convertible to/from a Json object. It has to be either a fundamental type or appropriate
to_json(json&, const value_t&)andfrom_json(const json&, value_t&)functions must be available. See the relevant nlohmann::json documentation for further information.A user-defined identifier is stored in the encoded Json object that is used to identify which value type is stored in the file. The identifier is checked for consistency when decoding the Json object.
- Template Parameters
value_t – value type stored in the geometry hierarchy map
Public Functions
-
inline GeometryHierarchyMapJsonConverter(std::string valueIdentifier)
Construct the converter.
- Parameters
valueIdentifier – user-defined identifier for the stored value
-
Container fromJson(const nlohmann::json &encoded) const
Decode a Json object into a geometry hierarchy map.
- Parameters
encoded – Json object that should be decoded
- Throws
std::invalid_argument – in case of format errors
- Returns
Decoded geometry hierarchy map
-
nlohmann::json toJson(const Container &container, const decorator_t *decorator) const
Encode the geometry hierarchy map into a Json object.
- Parameters
container – Geometry hierarchy map that should be encoded
decorator – nullptr or a decorator to add extra values to the json output
- Returns
Encoded Json object
Public Static Functions
-
static inline GeometryIdentifier decodeIdentifier(const nlohmann::json &encoded)
Decode a geometry identifier from a json object.
- Parameters
encoded – is the json object that carries the encoded identifier
- Returns
a valid geometry Identifier
-
static inline nlohmann::json encodeIdentifier(const GeometryIdentifier &id)
Encode the geometry identifier.
- Parameters
id – is the geometry identifier that will be encoded
-
class GeometryIdentifier
- #include <Acts/Geometry/GeometryIdentifier.hpp>
Identifier for geometry nodes within the geometry hierarchy.
An identifier can be split into the following components. They define a hierarchy of objects starting from the high-level volumes:
Volume
Boundary surfaces (for a volume)
Layers (confined within a volume)
Approach surfaces (for a layer)
Sensitive surfaces (confined to a layer, also called modules)
Public Types
-
using Value = uint64_t
Public Functions
-
GeometryIdentifier() = default
Construct default GeometryIdentifier with all values set to zero.
-
GeometryIdentifier(const GeometryIdentifier&) = default
-
GeometryIdentifier(GeometryIdentifier&&) = default
-
inline constexpr GeometryIdentifier(Value encoded)
Construct from an already encoded value.
-
~GeometryIdentifier() = default
-
inline constexpr Value approach() const
Return the approach identifier.
-
inline constexpr Value boundary() const
Return the boundary identifier.
-
inline constexpr Value extra() const
Return the extra identifier Usage can be experiment-specific, like tagging which kind of detector a surface object corresponds to, or which subsystem it belongs to.
-
inline constexpr Value layer() const
Return the layer identifier.
-
GeometryIdentifier &operator=(const GeometryIdentifier&) = default
-
GeometryIdentifier &operator=(GeometryIdentifier&&) = default
-
inline constexpr Value sensitive() const
Return the sensitive identifier.
-
inline constexpr GeometryIdentifier &setApproach(Value approach)
Set the approach identifier.
-
inline constexpr GeometryIdentifier &setBoundary(Value boundary)
Set the boundary identifier.
-
inline constexpr GeometryIdentifier &setExtra(Value extra)
Set the extra identifier.
-
inline constexpr GeometryIdentifier &setLayer(Value layer)
Set the layer identifier.
-
inline constexpr GeometryIdentifier &setSensitive(Value sensitive)
Set the sensitive identifier.
-
inline constexpr GeometryIdentifier &setVolume(Value volume)
Set the volume identifier.
-
inline constexpr Value value() const
Return the encoded value.
-
inline constexpr Value volume() const
Return the volume identifier.
-
struct GeometryIdentifierHook
- #include <Acts/Geometry/GeometryIdentifier.hpp>
Base class for hooks that can be used to modify the Geometry Identifier during construction.
Most common use case is setting the extra bit fields.
Public Functions
-
virtual ~GeometryIdentifierHook() = default
-
virtual Acts::GeometryIdentifier decorateIdentifier(Acts::GeometryIdentifier identifier, const Acts::Surface &surface) const
-
virtual ~GeometryIdentifierHook() = default
-
class GeometryObject
- #include <Acts/Geometry/GeometryObject.hpp>
Base class to provide GeometryIdentifier interface:
simple set and get
It also provides the binningPosition method for Geometry geometrical object to be binned in BinnedArrays
Subclassed by Acts::Layer, Acts::Surface, Acts::Volume
Public Functions
-
GeometryObject() = default
Defaulted constructor.
-
inline GeometryObject(const GeometryIdentifier &geometryId)
Constructor from a value.
- Parameters
geometryId – the geometry identifier of the object
-
GeometryObject(const GeometryObject&) = default
Defaulted copy constructor.
-
inline void assignGeometryId(const GeometryIdentifier &geometryId)
Set the value.
- Parameters
geometryId – the geometry identifier to be assigned
-
virtual Vector3 binningPosition(const GeometryContext &gctx, BinningValue bValue) const = 0
Force a binning position method.
- Parameters
gctx – The current geometry context object, e.g. alignment
bValue – is the value in which you want to bin
- Returns
vector 3D used for the binning schema
-
inline virtual double binningPositionValue(const GeometryContext &gctx, BinningValue bValue) const
Implement the binningValue.
- Parameters
gctx – The current geometry context object, e.g. alignment
bValue – is the dobule in which you want to bin
- Returns
float to be used for the binning schema
-
inline const GeometryIdentifier &geometryId() const
- Returns
the geometry id by reference
-
inline GeometryObject &operator=(const GeometryObject &geometryId)
Assignment operator.
- Parameters
geometryId – the source geometryId
-
template<class T>
class GeometryObjectSorterT - #include <Acts/Geometry/GeometryObjectSorter.hpp>
Public Functions
Constructor from a binning value.
- Parameters
gctx – The geometry context to use
bValue – is the value in which the binning is done
transform – is an optional transform to be performed
-
struct GeometryView3D
- #include <Acts/Visualization/GeometryView3D.hpp>
Public Static Functions
-
static void drawArrowBackward(IVisualization3D &helper, const Vector3 &start, const Vector3 &end, double arrowLength, double arrowWidth, const ViewConfig &viewConfig = s_viewLine)
Convenience function : arrow pointing back.
- Parameters
helper – [inout] The visualization helper
start – The start point
end – The end point
arrowLength – wrt thickness
arrowWidth – wrt thickness
viewConfig – The drawing configuration for this segment
-
static void drawArrowForward(IVisualization3D &helper, const Vector3 &start, const Vector3 &end, double arrowLength, double arrowWidth, const ViewConfig &viewConfig = s_viewLine)
Convenience function : arrow pointing forward.
- Parameters
helper – [inout] The visualization helper
start – The start point
end – The end point
arrowLength – wrt thickness
arrowWidth – wrt thickness
viewConfig – The drawing configuration for this segment
-
static void drawArrowsBoth(IVisualization3D &helper, const Vector3 &start, const Vector3 &end, double arrowLength, double arrowWidth, const ViewConfig &viewConfig = s_viewLine)
Convenience function : arrow pointing both directions.
- Parameters
helper – [inout] The visualization helper
start – The start point
end – The end point
arrowLength – wrt thickness
arrowWidth – wrt thickness
viewConfig – The drawing configuration for this segment
-
static void drawDetectorVolume(IVisualization3D &helper, const Acts::Experimental::DetectorVolume &volume, const GeometryContext &gctx, const Transform3 &transform = Transform3::Identity(), const ViewConfig &connected = ViewConfig({0, 255, 0}), const ViewConfig &unconnected = ViewConfig({255, 0, 0}), const ViewConfig &viewConfig = s_viewSensitive)
Helper method to draw DetectorVolume objects.
- Parameters
helper – [inout] The visualization helper
volume – The DetectorVolume to be drawn
gctx – The geometry context for which it is drawn
transform – An option additional transform
connected – The config for connected portals
unconnected – The config for unconnected portals
viewConfig – The drawing configuration
-
static void drawLayer(IVisualization3D &helper, const Layer &layer, const GeometryContext &gctx, const ViewConfig &layerConfig = s_viewPassive, const ViewConfig &sensitiveConfig = s_viewSensitive, const ViewConfig &gridConfig = s_viewGrid, const std::string &outputDir = ".")
Helper method to draw AbstractVolume objects.
- Parameters
helper – [inout] The visualization helper
layer – The tracking layer to be drawn
gctx – The geometry context for which it is drawn
layerConfig – The drawing configuration for passive surfaces
sensitiveConfig – The drawing configuration for sensitive surfaces
gridConfig – The drawing configuration for grid display
outputDir – Directory to write to
-
static void drawPolyhedron(IVisualization3D &helper, const Polyhedron &polyhedron, const ViewConfig &viewConfig = s_viewVolume)
Helper method to draw Polyhedron objects.
- Parameters
helper – [inout] The visualization helper
polyhedron – The surface to be drawn
viewConfig – The drawing configuration
-
static void drawPortal(IVisualization3D &helper, const Experimental::Portal &portal, const GeometryContext &gctx, const Transform3 &transform = Transform3::Identity(), const ViewConfig &connected = ViewConfig({0, 255, 0}), const ViewConfig &disconnected = ViewConfig({255, 0, 0}))
Helper method to draw portals objects.
- Parameters
helper – [inout] The visualization helper
portal – The portal to be drawn
gctx – The geometry context for which it is drawn
transform – An option additional transform
connected – The config for connected portals
disconnected – The config for disconnected portals
-
static void drawSegment(IVisualization3D &helper, const Vector3 &start, const Vector3 &end, const ViewConfig &viewConfig = s_viewLine)
Convenience function : line.
- Parameters
helper – [inout] The visualization helper
start – The start point
end – The end point
viewConfig – The drawing configuration for this segment
-
static void drawSegmentBase(IVisualization3D &helper, const Vector3 &start, const Vector3 &end, int arrows = 0, double arrowLength = 0., double arrowWidth = 0., const ViewConfig &viewConfig = s_viewLine)
Helper method to draw lines - base for all lines.
- Parameters
helper – [inout] The visualization helper
start – The start point
end – The end point
arrows – [ -1 | 0 | 1 | 2 ] = [ start | none | end | both ]
arrowLength – wrt halflength
arrowWidth – wrt thickness
viewConfig – The drawing configuration for this segment
-
static void drawSurface(IVisualization3D &helper, const Surface &surface, const GeometryContext &gctx, const Transform3 &transform = Transform3::Identity(), const ViewConfig &viewConfig = s_viewSensitive)
Helper method to draw Surface objects.
- Parameters
helper – [inout] The visualization helper
surface – The surface to be drawn
gctx – The geometry context for which it is drawn
transform – An option additional transform
viewConfig – The drawing configuration
-
static void drawSurfaceArray(IVisualization3D &helper, const SurfaceArray &surfaceArray, const GeometryContext &gctx, const Transform3 &transform = Transform3::Identity(), const ViewConfig &sensitiveConfig = s_viewSensitive, const ViewConfig &passiveConfig = s_viewPassive, const ViewConfig &gridConfig = s_viewGrid, const std::string &outputDir = ".")
Helper method to draw SurfaceArray objects.
- Parameters
helper – [inout] The visualization helper
surfaceArray – The surface to be drawn
gctx – The geometry context for which it is drawn
transform – An option additional transform
sensitiveConfig – The drawing configuration for sensitive surfaces
passiveConfig – The drawing configuration for passive surfaces
gridConfig – The drawing configuration for grid
outputDir – Directory to write to
-
static void drawTrackingVolume(IVisualization3D &helper, const TrackingVolume &tVolume, const GeometryContext &gctx, const ViewConfig &containerView = s_viewVolume, const ViewConfig &volumeView = s_viewVolume, const ViewConfig &layerView = s_viewPassive, const ViewConfig &sensitiveView = s_viewSensitive, const ViewConfig &gridView = s_viewGrid, bool writeIt = true, const std::string &tag = "", const std::string &outputDir = ".")
Helper method to draw AbstractVolume objects.
- Parameters
helper – [inout] The visualization helper
tVolume – The tracking volume to be drawn
gctx – The geometry context for which it is drawn
containerView – The drawing configuration for a container volume
volumeView – The drawing configuration for the navigation level volume
layerView – The drawing configuration for passive surfaces
sensitiveView – The drawing configuration for sensitive surfaces
gridView – The drawing configuration for grid display
writeIt – The prescription to write it or not
tag – The (optional) additional output tag
outputDir – Directory to write to
-
static void drawVolume(IVisualization3D &helper, const AbstractVolume &volume, const GeometryContext &gctx, const Transform3 &transform = Transform3::Identity(), const ViewConfig &viewConfig = s_viewVolume)
Helper method to draw AbstractVolume objects.
- Parameters
helper – [inout] The visualization helper
volume – The volume to be drawn
gctx – The geometry context for which it is drawn
transform – An option additional transform
viewConfig – The drawing configuration for boundary surfaces
-
static void drawArrowBackward(IVisualization3D &helper, const Vector3 &start, const Vector3 &end, double arrowLength, double arrowWidth, const ViewConfig &viewConfig = s_viewLine)
-
class GlueVolumesDescriptor
- #include <Acts/Geometry/GlueVolumesDescriptor.hpp>
Descriptor class to hold GlueVolumes of a TrackingGeometry object.
Should ease the wrapping of a TrackingGeometry object describing one Detector by another one.
Public Functions
-
GlueVolumesDescriptor() = default
Constructor.
Constructor - with arguments.
- Parameters
gvs – are the glue volume arrays mapped to the volume faces
-
~GlueVolumesDescriptor() = default
Destructor.
-
inline const std::vector<BoundarySurfaceFace> &glueFaces() const
Retrieve the available Glue Faces.
- Returns
the list of faces for which glue information is there
-
std::shared_ptr<const TrackingVolumeArray> glueVolumes(BoundarySurfaceFace bsf) const
Retrieve the glue volumes.
- Parameters
bsf – is the boundary surface face for which you want to get the array
- Returns
the shared pointer to the TrackingVolume array
Register the volumes.
- Parameters
bsf – is the boundary surface face where the volume array is attached
gvs – is the array of volumes to be attached
-
std::string screenOutput() const
Dump it to the screen.
-
GlueVolumesDescriptor() = default
-
class GraphConstructionBase
- #include <Acts/Plugins/ExaTrkX/Stages.hpp>
Subclassed by Acts::OnnxMetricLearning, Acts::TorchMetricLearning
Public Functions
-
virtual ~GraphConstructionBase() = default
-
virtual std::tuple<std::any, std::any> operator()(std::vector<float> &inputValues, std::size_t numNodes) = 0
Perform the graph construction.
- Parameters
inputValues – Flattened input data
numNodes – number of nodes. inputValues.size() / numNodes then gives the number of features
- Returns
(node_tensor, edge_tensore)
-
virtual ~GraphConstructionBase() = default
-
class GreedyAmbiguityResolution
- #include <Acts/AmbiguityResolution/GreedyAmbiguityResolution.hpp>
Evicts tracks that seem to be duplicates or fakes.
This algorithm takes a greedy approach in the sense that it will remove the track which looks “most
duplicate/fake” first and continues the same process with the rest. That process continues until the final state conditions are met.
The implementation works as follows: 1) Calculate shared hits per track. 2) If the maximum shared hits criteria is met, we are done. This is the configurable amount of shared hits we are ok with in our experiment. 3) Else, remove the track with the highest relative shared hits (i.e. shared hits / hits). 4) Back to square 1.
Public Functions
-
inline GreedyAmbiguityResolution(const Config &cfg, std::unique_ptr<const Logger> logger = getDefaultLogger("GreedyAmbiguityResolution", Logging::INFO))
-
template<typename track_container_t, typename traj_t, template<typename> class holder_t, typename source_link_hash_t, typename source_link_equality_t>
void computeInitialState(const TrackContainer<track_container_t, traj_t, holder_t> &tracks, State &state, source_link_hash_t &&sourceLinkHash, source_link_equality_t &&sourceLinkEquality) const Computes the initial state for the input data.
This function accumulates information that will later be used to accelerate the ambiguity resolution.
- Parameters
tracks – The input track container.
state – An empty state object which is expected to be default constructed.
sourceLinkHash – A functor to acquire a hash from a given source link.
sourceLinkEquality – A functor to check equality of two source links.
-
void resolve(State &state) const
Updates the state iteratively by evicting one track after the other until the final state conditions are met.
- Parameters
state – A state object that was previously filled by the initialization.
-
struct Config
- #include <Acts/AmbiguityResolution/GreedyAmbiguityResolution.hpp>
Public Members
-
std::uint32_t maximumIterations = 1000
Maximum number of iterations.
Maximum amount of shared hits per track.
-
size_t nMeasurementsMin = 7
Minimum number of measurement to form a track.
-
std::uint32_t maximumIterations = 1000
-
struct State
- #include <Acts/AmbiguityResolution/GreedyAmbiguityResolution.hpp>
Public Members
-
std::vector<std::vector<std::size_t>> measurementsPerTrack
-
std::size_t numberOfTracks = {}
-
boost::container::flat_set<std::size_t> selectedTracks
-
std::vector<float> trackChi2
-
boost::container::flat_map<std::size_t, boost::container::flat_set<std::size_t>> tracksPerMeasurement
-
std::vector<int> trackTips
-
std::vector<std::vector<std::size_t>> measurementsPerTrack
-
inline GreedyAmbiguityResolution(const Config &cfg, std::unique_ptr<const Logger> logger = getDefaultLogger("GreedyAmbiguityResolution", Logging::INFO))
-
template<int mainGridSize = 2000, int trkGridSize = 15, typename vfitter_t = DummyVertexFitter<>>
class GridDensityVertexFinder - #include <Acts/Vertexing/GridDensityVertexFinder.hpp>
Vertex finder that makes use of a track density grid.
Each single track is modelled as a 2(!)-dim Gaussian distribution grid in the d0-z0 plane, but only the overlap with the z-axis (i.e. a 1-dim density vector) needs to be calculated. All track contributions along the beam axis (main density grid) a superimposed and the z-value of the bin with the highest track density is returned as a vertex candidate.
- Template Parameters
mainGridSize – The size of the z-axis 1-dim main density grid
trkGridSize – The 2(!)-dim grid size of a single track, i.e. a single track is modelled as a (trkGridSize x trkGridSize) grid in the d0-z0 plane. Note: trkGridSize has to be an odd value.
Public Types
-
using MainGridVector = typename GridDensity::MainGridVector
-
using TrackGridVector = typename GridDensity::TrackGridVector
Public Functions
-
template<typename T = InputTrack_t, std::enable_if_t<std::is_same<T, BoundTrackParameters>::value, int> = 0>
inline GridDensityVertexFinder() Default constructor used if InputTrack_t type == BoundTrackParameters.
-
template<typename T = InputTrack_t, std::enable_if_t<std::is_same<T, BoundTrackParameters>::value, int> = 0>
inline GridDensityVertexFinder(const Config &cfg) Constructor used if InputTrack_t type == BoundTrackParameters.
- Parameters
cfg – Configuration object
-
inline GridDensityVertexFinder(const Config &cfg, const std::function<BoundTrackParameters(InputTrack_t)> &func)
Constructor for user-defined InputTrack_t type =! BoundTrackParameters.
- Parameters
cfg – Configuration object
func – Function extracting BoundTrackParameters from InputTrack_t object
-
inline GridDensityVertexFinder(const std::function<BoundTrackParameters(InputTrack_t)> &func)
Constructor for user-defined InputTrack_t type =! BoundTrackParameters with default Config object.
- Parameters
func – Function extracting BoundTrackParameters from InputTrack_t object
-
Result<std::vector<Vertex<InputTrack_t>>> find(const std::vector<const InputTrack_t*> &trackVector, const VertexingOptions<InputTrack_t> &vertexingOptions, State &state) const
Function that finds single vertex candidate.
- Parameters
trackVector – Input track collection
vertexingOptions – Vertexing options
state – The state object to cache the density grid and density contributions of each track, to be used if cacheGridStateForTrackRemoval == true
- Returns
Vector of vertices, filled with a single vertex (for consistent interfaces)
-
struct Config
- #include <Acts/Vertexing/GridDensityVertexFinder.hpp>
The Config struct.
Public Functions
-
inline Config(const GridDensity &gDensity)
- Parameters
gDensity – The grid density
-
inline Config(float zMinMax = 100)
- Parameters
zMinMax – min and max z value of big z-axis grid
Public Members
-
bool cacheGridStateForTrackRemoval = true
-
double d0SignificanceCut = maxD0TrackSignificance * maxD0TrackSignificance
-
bool estimateSeedWidth = false
-
GridDensity gridDensity
-
double maxD0TrackSignificance = 3.5
-
double maxZ0TrackSignificance = 12.
-
double z0SignificanceCut = maxZ0TrackSignificance * maxZ0TrackSignificance
-
inline Config(const GridDensity &gDensity)
-
struct State
- #include <Acts/Vertexing/GridDensityVertexFinder.hpp>
The State struct.
Only needed if cacheGridStateForTrackRemoval == true
Public Members
-
std::map<const InputTrack_t*, std::pair<int, TrackGridVector>> binAndTrackGridMap
-
bool isInitialized = false
-
MainGridVector mainGrid = MainGridVector::Zero()
-
std::map<const InputTrack_t*, bool> trackSelectionMap
-
std::vector<const InputTrack_t*> tracksToRemove
-
std::map<const InputTrack_t*, std::pair<int, TrackGridVector>> binAndTrackGridMap
-
template<typename propagator_t, typename propagator_options_t = PropagatorOptions<>>
class HelicalTrackLinearizer - #include <Acts/Vertexing/HelicalTrackLinearizer.hpp>
Linearizes the track parameters at the PCA to a user-provided point (linPoint).
The track parameters are written as a function of the global PCA position and the momentum of the particle at the PCA. The linearization then reads (see Eq. 5.7 in Ref. (1)):
q = A (r - r_0) + B (p - p_0) + c,
where q are the Perigee parameters wrt linPoint, {r_0} r is the {initial} 4D PCA position, {p_0} p is the {initial} momentum (phi, theta, q/p) at the PCA, and c is the constant term of the expansion. A and B are matrices of derivatives, denoted hereafter as “positionJacobian” and “momentumJacobian” respectively.
This class computes A and B using the analytic formulae of Ref. (1).
Ref. (1) - CERN-THESIS-2010-027, Giacinto Piacquadio (Freiburg U.)
- Template Parameters
propagator_t – Propagator type
propagator_options_t – Propagator options type
Public Types
-
using Propagator_t = propagator_t
Public Functions
-
inline HelicalTrackLinearizer(const Config &config, std::unique_ptr<const Logger> _logger = getDefaultLogger("HelTrkLinProp", Logging::INFO))
Constructor.
- Parameters
config – Configuration object
_logger – a logger instance
-
Result<LinearizedTrack> linearizeTrack(const BoundTrackParameters ¶ms, const Vector4 &linPoint, const Acts::GeometryContext &gctx, const Acts::MagneticFieldContext &mctx, State &state) const
Function that linearizes BoundTrackParameters at the PCA to a given Perigee surface.
Note
Transverse plane of the Perigee corresponding to
linPointis parallel to the global x-y plane- Parameters
params – Parameters to linearize
linPoint – Point which defines the Perigee.
gctx – Geometry context
mctx – Magnetic field context
state – Linearizer state object
- Returns
Linearized track
-
struct Config
- #include <Acts/Vertexing/HelicalTrackLinearizer.hpp>
Configuration struct.
Public Functions
@ Config constructor if magnetic field is present
- Parameters
bIn – The magnetic field
prop – The propagator
Config constructor without B field -> uses NullBField.
- Parameters
prop – The propagator
Public Members
-
std::shared_ptr<const MagneticFieldProvider> bField
-
double minQoP = 1e-15
-
std::shared_ptr<const Propagator_t> propagator
-
ActsScalar targetTolerance = 1e-12
Tolerance determining how close we need to get to the Perigee surface to reach it during propagation.
-
struct State
- #include <Acts/Vertexing/HelicalTrackLinearizer.hpp>
State struct.
Public Functions
-
inline State(MagneticFieldProvider::Cache fieldCacheIn)
The state constructor.
- Parameters
fieldCacheIn – The magnetic field cache
Public Members
-
MagneticFieldProvider::Cache fieldCache
Magnetic field cache.
-
inline State(MagneticFieldProvider::Cache fieldCacheIn)
-
class HomogeneousSurfaceMaterial : public Acts::ISurfaceMaterial
- #include <Acts/Material/HomogeneousSurfaceMaterial.hpp>
It extends the ISurfaceMaterial virtual base class to describe a simple homogeneous material on a surface.
Public Functions
-
HomogeneousSurfaceMaterial() = default
Default Constructor - defaulted.
-
HomogeneousSurfaceMaterial(const HomogeneousSurfaceMaterial &hsm) = default
Copy Constructor.
- Parameters
hsm – is the source material
-
HomogeneousSurfaceMaterial(const MaterialSlab &full, double splitFactor = 1., MappingType mappingType = MappingType::Default)
Explicit constructor.
- Parameters
full – are the full material properties
splitFactor – is the split for pre/post update
mappingType – is the type of surface mapping associated to the surface
-
HomogeneousSurfaceMaterial(HomogeneousSurfaceMaterial &&hsm) = default
Copy Move Constructor.
- Parameters
hsm – is the source material
-
~HomogeneousSurfaceMaterial() override = default
Destructor.
-
inline double factor(Direction pDir, MaterialUpdateStage mStage) const
The inherited methods - for scale access.
-
inline virtual const MaterialSlab &materialSlab(const Vector2 &lp) const final
Return method for full material description of the Surface.
from local coordinate on the surface
Note
the input parameter is ignored
- Parameters
lp – is the local position used for the (eventual) lookup
- Returns
const MaterialSlab
-
const MaterialSlab &materialSlab(const Vector2 &lp) const = 0
The inherited methods - for MaterialSlab access.
-
inline MaterialSlab materialSlab(const Vector2 &lp, Direction pDir, MaterialUpdateStage mStage) const
The inherited methods - for MaterialSlab access.
-
inline virtual const MaterialSlab &materialSlab(const Vector3 &gp) const final
Return method for full material description of the Surface.
from the global coordinates
Note
the input parameter is ignored
- Parameters
gp – is the global position used for the (eventual) lookup
- Returns
const MaterialSlab
-
const MaterialSlab &materialSlab(const Vector3 &gp) const = 0
The inherited methods - for MaterialSlab access.
-
inline MaterialSlab materialSlab(const Vector3 &gp, Direction pDir, MaterialUpdateStage mStage) const
The inherited methods - for MaterialSlab access.
-
inline virtual const MaterialSlab &materialSlab(size_t bin0, size_t bin1) const final
Direct access via bins to the MaterialSlab.
Note
the input parameters are ignored
- Parameters
bin0 – is the material bin in dimension 0
bin1 – is the material bin in dimension 1
-
const MaterialSlab &materialSlab(size_t bin0, size_t bin1) const = 0
The inherited methods - for MaterialSlab access.
-
virtual HomogeneousSurfaceMaterial &operator*=(double scale) final
Scale operator.
it is effectively a thickness scaling
- Parameters
scale – is the scale factor
-
HomogeneousSurfaceMaterial &operator=(const HomogeneousSurfaceMaterial &hsm) = default
Assignment operator.
- Parameters
hsm – is the source material
-
HomogeneousSurfaceMaterial &operator=(HomogeneousSurfaceMaterial &&hsm) = default
Assignment Move operator.
- Parameters
hsm – is the source material
-
inline bool operator==(const HomogeneousSurfaceMaterial &hsm) const
Equality operator.
- Parameters
hsm – is the source material
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
- Parameters
sl – The outoput stream
-
HomogeneousSurfaceMaterial() = default
-
class HomogeneousVolumeMaterial : public Acts::IVolumeMaterial
- #include <Acts/Material/HomogeneousVolumeMaterial.hpp>
It extends the IVolumeMaterial base class to describe a simple homogeneous material in a volume.
Public Functions
-
HomogeneousVolumeMaterial(const HomogeneousVolumeMaterial &hvm) = default
Copy Constructor.
- Parameters
hvm – is the source material
-
HomogeneousVolumeMaterial(const Material &material)
Explicit constructor.
- Parameters
material – is the material held by this
-
HomogeneousVolumeMaterial(HomogeneousVolumeMaterial &&hvm) = default
Copy Move Constructor.
- Parameters
hvm – is the source material
-
~HomogeneousVolumeMaterial() override = default
Destructor.
-
inline virtual const Material material(const Vector3 &position) const final
Access to actual material.
Note
positionis ignored- Parameters
position – is the request position for the material call
-
HomogeneousVolumeMaterial &operator=(const HomogeneousVolumeMaterial &hvm) = default
Assignment operator.
- Parameters
hvm – is the source material
-
inline bool operator==(const HomogeneousVolumeMaterial &hvm) const
Equality operator.
- Parameters
hvm – is the source material
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
- Parameters
sl – The outoput stream
-
HomogeneousVolumeMaterial(const HomogeneousVolumeMaterial &hvm) = default
-
class IAxis
- #include <Acts/Utilities/IAxis.hpp>
Common base class for all Axis instance.
This allows generice handling such as for inspection.
Public Functions
-
virtual std::vector<ActsScalar> getBinEdges() const = 0
Return a vector of bin edges.
- Returns
Vector which contains the bin edges
-
virtual detail::AxisBoundaryType getBoundaryType() const = 0
returns the boundary type set in the template param
- Returns
AxisBoundaryTypeof this axis
-
virtual ActsScalar getMax() const = 0
get maximum of binning range
- Returns
maximum of binning range
-
virtual ActsScalar getMin() const = 0
get minimum of binning range
- Returns
minimum of binning range
-
virtual size_t getNBins() const = 0
get total number of bins
- Returns
total number of bins (excluding under-/overflow bins)
-
virtual bool isEquidistant() const = 0
returns whether the axis is equidistant
- Returns
bool is equidistant
-
virtual bool isVariable() const = 0
returns whether the axis is variable
- Returns
bool is variable
-
virtual std::vector<ActsScalar> getBinEdges() const = 0
-
class IConfinedTrackingVolumeBuilder
- #include <Acts/Geometry/IConfinedTrackingVolumeBuilder.hpp>
This is an interface class for constructing TrackingVolumes whose are confined in a mother-TrackingVolume.
Subclassed by Acts::DD4hepVolumeBuilder
Public Functions
-
virtual ~IConfinedTrackingVolumeBuilder() = default
Virtual destructor.
-
virtual MutableTrackingVolumeVector centralVolumes() const = 0
Interface for constructing a vector of confined TrackingVolumes.
-
virtual const std::string &identification() const = 0
Interface for retrieving the identification string of the confined volumes.
-
virtual ~IConfinedTrackingVolumeBuilder() = default
-
class IdentifiedDetectorElement : public DetectorElementBase
- #include <Acts/Plugins/Identification/IdentifiedDetectorElement.hpp>
The identified detector element.
It adds the Identifier defnition and a forward declaration of the DigitizationModule to the detector elements
The identifier can be overwritten with by the use of the ACTS_CORE_IDENTIFIER_PLUGIN
Subclassed by Acts::TGeoDetectorElement
Public Functions
-
virtual const std::shared_ptr<const DigitizationModule> digitizationModule() const = 0
Retrieve the DigitizationModule.
-
virtual Identifier identifier() const = 0
Retrieve the Identifier.
-
virtual const std::shared_ptr<const DigitizationModule> digitizationModule() const = 0
-
struct Identity
- #include <Acts/Utilities/Identity.hpp>
Function object which maps a value to itself by perfect forwarding This is a backport of C++20’s std::identity.
Public Functions
-
template<typename T>
inline constexpr auto operator()(T &&v) const
-
template<typename T>
-
template<typename SpacePoint>
class IExperimentCuts - #include <Acts/Seeding/IExperimentCuts.hpp>
IExperimentCutscan be used to increase or decrease seed weights based on the space points used in a seed.Seed weights are also influenced by the SeedFilter default implementation. This tool is also used to decide if a seed passes a seed weight cut. As the weight is stored in seeds, there are two distinct methods.
Public Functions
-
virtual ~IExperimentCuts() = default
-
virtual std::vector<typename CandidatesForMiddleSp<const InternalSpacePoint<SpacePoint>>::value_type> cutPerMiddleSP(std::vector<typename CandidatesForMiddleSp<const InternalSpacePoint<SpacePoint>>::value_type> seedCandidates) const = 0
- Parameters
seedCandidates – contains collection of seed candidates created for one middle space point in a std::tuple format
- Returns
vector of seed candidates that pass the cut
-
virtual float seedWeight(const InternalSpacePoint<SpacePoint> &bottom, const InternalSpacePoint<SpacePoint> &middle, const InternalSpacePoint<SpacePoint> &top) const = 0
Returns seed weight bonus/malus depending on detector considerations.
- Parameters
bottom – bottom space point of the current seed
middle – middle space point of the current seed
top – top space point of the current seed
- Returns
seed weight to be added to the seed’s weight
-
virtual bool singleSeedCut(float weight, const InternalSpacePoint<SpacePoint> &bottom, const InternalSpacePoint<SpacePoint> &middle, const InternalSpacePoint<SpacePoint> &top) const = 0
- Parameters
weight – the current seed weight
bottom – bottom space point of the current seed
middle – middle space point of the current seed
top – top space point of the current seed
- Returns
true if the seed should be kept, false if the seed should be discarded
-
virtual ~IExperimentCuts() = default
-
class ILayerArrayCreator
- #include <Acts/Geometry/ILayerArrayCreator.hpp>
Interface class ILayerArrayCreators, it inherits from IAlgTool.
It receives the LayerVector and creaets an array with NaivgationLayer objects filled in between.
Subclassed by Acts::LayerArrayCreator
Public Functions
-
virtual ~ILayerArrayCreator() = default
Virtual destructor.
-
virtual std::unique_ptr<const LayerArray> layerArray(const GeometryContext &gctx, const LayerVector &layers, double min, double max, BinningType btype = arbitrary, BinningValue bvalue = binX) const = 0
LayerArrayCreator interface method.
- Parameters
gctx – is the geometry context for witch the volume is built
layers – are the layers to be moved into an array
min – is the minimul value for binning
max – is the maximum value for binning
btype – is the binning type
bvalue – is the value in which the binning should be done
- Returns
unique pointer to a new LayerArray
-
virtual ~ILayerArrayCreator() = default
-
class ILayerBuilder
- #include <Acts/Geometry/ILayerBuilder.hpp>
Interface class for ILayerBuilders in a typical | EC- | Central | EC+ | detector setup.
Subclassed by Acts::DD4hepLayerBuilder, Acts::PassiveLayerBuilder, Acts::TGeoLayerBuilder
Public Functions
-
virtual ~ILayerBuilder() = default
Virtual destructor.
-
virtual const LayerVector centralLayers(const GeometryContext &gctx) const = 0
LayerBuilder interface method.
- Parameters
gctx – is the geometry context under which the geometry is built
- Returns
the layers at the central sector
-
virtual const std::string &identification() const = 0
Name identification.
- Returns
the string based identification
-
virtual const LayerVector negativeLayers(const GeometryContext &gctx) const = 0
LayerBuilder interface method.
- Parameters
gctx – is the geometry context under which the geometry is built
- Returns
the layers at negative side
-
virtual const LayerVector positiveLayers(const GeometryContext &gctx) const = 0
LayerBuilder interface method.
- Parameters
gctx – is the geometry context under which the geometry is built
- Returns
the layers at positive side
-
virtual ~ILayerBuilder() = default
-
class IMaterialDecorator
- #include <Acts/Material/IMaterialDecorator.hpp>
Virtual base class for decorators that allow to load material onto a TrackingGeometry.
The geometry allows material to be assigned either to surfaces or to volumes, hence there are two decorate interface methods.
Subclassed by Acts::JsonMaterialDecorator
Public Functions
-
virtual ~IMaterialDecorator() = default
Virtual Destructor.
-
virtual void decorate(Surface &surface) const = 0
Decorate a surface.
- Parameters
surface – the non-cost surface that is decorated
-
virtual void decorate(TrackingVolume &volume) const = 0
Decorate a TrackingVolume.
- Parameters
volume – the non-cost volume that is decorated
-
virtual ~IMaterialDecorator() = default
-
struct ImpactParametersAndSigma
- #include <Acts/Vertexing/ImpactPointEstimator.hpp>
Public Members
-
double IPd0 = 0.
-
double IPz0 = 0.
-
double IPz0SinTheta = 0.
-
double PVsigmad0 = 0.
-
double PVsigmaz0 = 0.
-
double PVsigmaz0SinTheta = 0.
-
double sigmad0 = 0.
-
double sigmaz0 = 0.
-
double sigmaz0SinTheta = 0.
-
double IPd0 = 0.
-
template<typename input_track_t, typename propagator_t, typename propagator_options_t = PropagatorOptions<>>
class ImpactPointEstimator - #include <Acts/Vertexing/ImpactPointEstimator.hpp>
Estimator for impact point calculations.
Public Functions
-
inline ImpactPointEstimator(const Config &cfg)
Constructor.
- Parameters
cfg – Configuration object
-
Result<double> calculate3dDistance(const GeometryContext &gctx, const BoundTrackParameters &trkParams, const Vector3 &vtxPos, State &state) const
Calculates 3D distance between a track and a 3D point.
- Parameters
gctx – The geometry context
trkParams – Track parameters
vtxPos – Position to calculate distance to
state – The state object
- Returns
Distance
-
Result<BoundTrackParameters> estimate3DImpactParameters(const GeometryContext &gctx, const Acts::MagneticFieldContext &mctx, const BoundTrackParameters &trkParams, const Vector3 &vtxPos, State &state) const
Creates track parameters bound to plane at point of closest approach in 3d to given reference position.
The parameters and errors are defined on the plane intersecting the track at point of closest approach, with track orthogonal to the plane and center of the plane defined as the given reference point (vertex).
- Parameters
gctx – The geometry context
mctx – The magnetic field context
trkParams – Track parameters
vtxPos – Reference position (vertex)
state – The state object
- Returns
New track params
-
Result<ImpactParametersAndSigma> estimateImpactParameters(const BoundTrackParameters &track, const Vertex<input_track_t> &vtx, const GeometryContext &gctx, const MagneticFieldContext &mctx) const
Estimates the impact parameters and their errors of a given track w.r.t.
a vertex by propagating the trajectory state towards the vertex position.
- Parameters
track – Track to estimate IP from
vtx – Vertex the track belongs to
gctx – The geometry context
mctx – The magnetic field context
-
Result<double> get3DLifetimeSignOfTrack(const BoundTrackParameters &track, const Vertex<input_track_t> &vtx, const Acts::Vector3 &direction, const GeometryContext &gctx, const MagneticFieldContext &mctx) const
Estimates the sign of the 3D lifetime of a given track w.r.t.
a vertex and a direction (e.g. a jet direction)
- Parameters
track – Track to estimate the IP from
vtx – Vertex the track belongs to
direction – The direction
gctx – The geometry context
mctx – The magnetic field context
- Returns
The value of the 3D lifetime
-
Result<double> get3dVertexCompatibility(const GeometryContext &gctx, const BoundTrackParameters *trkParams, const Vector3 &vertexPos) const
Estimates the compatibility of a track to a vertex position based on the 3d distance between the track and the vertex.
- Parameters
gctx – The Geometry context
trkParams – Track parameters at point of closest approach in 3d as retrieved by estimate3DImpactParameters
vertexPos – The vertex position
- Returns
The compatibility value
-
Result<std::pair<double, double>> getLifetimesSignOfTrack(const BoundTrackParameters &track, const Vertex<input_track_t> &vtx, const Acts::Vector3 &direction, const GeometryContext &gctx, const MagneticFieldContext &mctx) const
Estimates the sign of the 2D and Z lifetime of a given track w.r.t.
a vertex and a direction (e.g. a jet direction) by propagating the trajectory state towards the vertex position and computing the scalar product with the direction vector
- Parameters
track – Track to estimate the IP from
vtx – Vertex the track belongs to
direction – The direction
gctx – The geometry context
mctx – The magnetic field context
- Returns
A pair holding the sign for the 2D an Z lifetimes
-
struct Config
- #include <Acts/Vertexing/ImpactPointEstimator.hpp>
Public Functions
Config constructor if magnetic field is present.
- Parameters
bIn – The magnetic field
prop – The propagator
Config constructor without B field -> uses NullBField provided)
- Parameters
prop – The propagator
Public Members
-
std::shared_ptr<const MagneticFieldProvider> bField
Magnetic field.
-
int maxIterations = 20
Max. number of iterations in Newton method.
-
double maxRho = 1e+15
Maximum curvature value.
-
double minQoP = 1e-15
Minimum q/p value.
-
double precision = 1.e-10
Desired precision in deltaPhi in Newton method.
-
std::shared_ptr<const propagator_t> propagator
Propagator.
-
struct State
- #include <Acts/Vertexing/ImpactPointEstimator.hpp>
State struct.
Public Functions
-
inline State(MagneticFieldProvider::Cache fieldCacheIn)
The state constructor.
- Parameters
fieldCacheIn – The magnetic field cache
Public Members
-
MagneticFieldProvider::Cache fieldCache
Magnetic field cache.
-
inline State(MagneticFieldProvider::Cache fieldCacheIn)
-
inline ImpactPointEstimator(const Config &cfg)
-
class InfiniteBounds : public Acts::SurfaceBounds
- #include <Acts/Surfaces/InfiniteBounds.hpp>
templated boundless extension to forward the interface Returns all inside checks to true and can templated for all bounds
Public Functions
-
InfiniteBounds() = default
-
~InfiniteBounds() override = default
-
inline virtual bool inside(const Vector2&, const BoundaryCheck&) const final
Method inside() returns true for any case.
ignores input parameters
- Returns
always true
-
inline virtual std::ostream &toStream(std::ostream &os) const final
Output Method for std::ostream.
-
inline virtual SurfaceBounds::BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Access method for bound values, this is a dynamically sized vector containing the parameters needed to describe these bounds.
- Returns
of the stored values for this SurfaceBounds object
-
InfiniteBounds() = default
-
template<typename SpacePoint>
class InternalSeed - #include <Acts/Seeding/InternalSeed.hpp>
Public Functions
-
InternalSeed(InternalSpacePoint<SpacePoint> &s0, InternalSpacePoint<SpacePoint> &s1, InternalSpacePoint<SpacePoint> &s2, float z, bool qualitySeed = false)
-
InternalSeed &operator=(const InternalSeed &seed)
-
inline bool qualitySeed() const
-
inline float z() const
Public Members
-
const std::array<InternalSpacePoint<SpacePoint>*, 3> sp
-
InternalSeed(InternalSpacePoint<SpacePoint> &s0, InternalSpacePoint<SpacePoint> &s1, InternalSpacePoint<SpacePoint> &s2, float z, bool qualitySeed = false)
-
template<typename SpacePoint>
class InternalSpacePoint - #include <Acts/Seeding/InternalSpacePoint.hpp>
Public Functions
-
InternalSpacePoint() = delete
-
inline InternalSpacePoint(const InternalSpacePoint<SpacePoint> &sp)
-
inline InternalSpacePoint(std::size_t index, const SpacePoint &sp, const Acts::Vector3 &globalPos, const Acts::Vector2 &offsetXY, const Acts::Vector2 &variance)
-
~InternalSpacePoint() = default
-
inline std::size_t index() const
-
InternalSpacePoint<SpacePoint> &operator=(const InternalSpacePoint<SpacePoint>&) = delete
-
inline float phi() const
-
inline const float &radius() const
-
inline const SpacePoint &sp() const
-
inline const float &varianceR() const
-
inline const float &varianceZ() const
-
inline const float &x() const
-
inline const float &y() const
-
inline const float &z() const
-
InternalSpacePoint() = delete
-
template<typename grid_t>
class InterpolatedBFieldMap : public Acts::InterpolatedMagneticField - #include <Acts/MagneticField/InterpolatedBFieldMap.hpp>
interpolate magnetic field value from field values on a given grid
This class implements a magnetic field service which is initialized by a field map defined by:
a list of field values on a regular grid in some n-Dimensional space,
a transformation of global 3D coordinates onto this n-Dimensional space.
a transformation of local n-Dimensional magnetic field coordinates into global (cartesian) 3D coordinates
The magnetic field value for a given global position is then determined by:
mapping the position onto the grid,
looking up the magnetic field values on the closest grid points,
doing a linear interpolation of these magnetic field values.
- Template Parameters
grid_t – The Grid type which provides the field storage and interpolation
Public Functions
-
inline InterpolatedBFieldMap(Config cfg)
default constructor
-
inline Result<Vector3> getField(const Vector3 &position) const
retrieve field at given position
- Parameters
position – [in] global 3D position
- Returns
magnetic field value at the given position
- Pre
The given
positionmust lie within the range of the underlying magnetic field map.
-
inline virtual Result<Vector3> getField(const Vector3 &position, MagneticFieldProvider::Cache &cache) const final
Retrieve magnetic field value at a given location.
Requires a cache object created through makeCache().
- Parameters
position – [in] global 3D position for the lookup
cache – [inout] Field provider specific cache object
- Returns
magnetic field vector at given position
-
inline Result<FieldCell> getFieldCell(const Vector3 &position) const
retrieve field cell for given position
- Parameters
position – [in] global 3D position
- Returns
field cell containing the given global position
- Pre
The given
positionmust lie within the range of the underlying magnetic field map.
-
inline virtual Result<Vector3> getFieldGradient(const Vector3 &position, ActsMatrix<3, 3> &derivative, MagneticFieldProvider::Cache &cache) const final
Retrieve magnetic field value its its gradient.
Requires a cache object created through makeCache().
Note
currently the derivative is not calculated
Note
Cache is not used currently
- Parameters
position – [in] global 3D position
derivative – [out] gradient of magnetic field vector as (3x3) matrix
cache – [inout] Field provider specific cache object
- Returns
magnetic field vector
-
inline virtual Vector3 getFieldUnchecked(const Vector3 &position) const final
Get a field value without checking if the lookup position is within the interpolation domain.
- Parameters
position – The lookup position in 3D
- Returns
The field value at
position
-
inline const Grid &getGrid() const
Get a const reference on the underlying grid structure.
- Returns
grid reference
-
inline virtual std::vector<double> getMax() const final
get the maximum value of all axes of the field map
- Returns
vector returning the maxima of all field map axes
-
inline virtual std::vector<double> getMin() const final
get the minimum value of all axes of the field map
- Returns
vector returning the minima of all field map axes
-
inline virtual std::vector<size_t> getNBins() const final
get the number of bins for all axes of the field map
- Returns
vector returning number of bins for all field map axes
-
inline virtual bool isInside(const Vector3 &position) const final
check whether given 3D position is inside look-up domain
- Parameters
position – [in] global 3D position
- Returns
trueif position is inside the defined look-up grid, otherwisefalse
-
inline bool isInsideLocal(const ActsVector<DIM_POS> &gridPosition) const
check whether given 3D position is inside look-up domain
- Parameters
gridPosition – [in] local N-D position
- Returns
trueif position is inside the defined look-up grid, otherwisefalse
-
inline virtual MagneticFieldProvider::Cache makeCache(const MagneticFieldContext &mctx) const final
Make an opaque cache for the magnetic field.
Instructs the specific implementation to generate a
Cacheinstance for magnetic field lookup.- Parameters
mctx – The magnetic field context to generate cache for
- Returns
Cache The opaque cache object
Public Static Attributes
-
static constexpr size_t DIM_POS = Grid::DIM
-
struct Cache
- #include <Acts/MagneticField/InterpolatedBFieldMap.hpp>
Public Functions
-
inline Cache(const MagneticFieldContext &mctx)
Constructor with magnetic field context.
- Parameters
mctx – the magnetic field context
-
inline Cache(const MagneticFieldContext &mctx)
-
struct Config
- #include <Acts/MagneticField/InterpolatedBFieldMap.hpp>
Config structure for the interpolated B field map.
Public Members
-
Grid grid
grid storing magnetic field values
-
double scale = 1.
global B-field scaling factor
Note
Negative values for
scaleare accepted and will invert the direction of the magnetic field.
-
std::function<Vector3(const FieldType&, const Vector3&)> transformBField
calculating the global 3D coordinates (cartesian) of the magnetic field with the local n dimensional field and the global 3D position as input
- std::function< ActsVector< DIM_POS >const Vector3 &)> transformPos
mapping of global 3D coordinates (cartesian) onto grid space
-
Grid grid
-
struct FieldCell
- #include <Acts/MagneticField/InterpolatedBFieldMap.hpp>
struct representing smallest grid unit in magnetic field grid
This type encapsulate all required information to perform linear interpolation of magnetic field values within a confined 3D volume.
Public Functions
-
inline FieldCell(std::array<double, DIM_POS> lowerLeft, std::array<double, DIM_POS> upperRight, std::array<Vector3, N> fieldValues)
default constructor
- Parameters
lowerLeft – [in] generalized lower-left corner of hyper box (containing the minima of the hyper box along each Dimension)
upperRight – [in] generalized upper-right corner of hyper box (containing the maxima of the hyper box along each Dimension)
fieldValues – [in] field values at the hyper box corners sorted in the canonical order defined in Acts::interpolate
-
inline Vector3 getField(const ActsVector<DIM_POS> &position) const
retrieve field at given position
- Parameters
position – [in] global 3D position
- Returns
magnetic field value at the given position
- Pre
The given
positionmust lie within the current field cell.
-
inline bool isInside(const ActsVector<DIM_POS> &position) const
check whether given 3D position is inside this field cell
- Parameters
position – [in] global 3D position
- Returns
trueif position is inside the current field cell, otherwisefalse
Public Static Attributes
-
static constexpr unsigned int N = 1 << DIM_POS
number of corner points defining the confining hyper-box
-
inline FieldCell(std::array<double, DIM_POS> lowerLeft, std::array<double, DIM_POS> upperRight, std::array<Vector3, N> fieldValues)
-
class InterpolatedMagneticField : public Acts::MagneticFieldProvider
- #include <Acts/MagneticField/InterpolatedBFieldMap.hpp>
Subclassed by Acts::InterpolatedBFieldMap< grid_t >
Public Functions
-
virtual Vector3 getFieldUnchecked(const Vector3 &position) const = 0
Get a field value without checking if the lookup position is within the interpolation domain.
- Parameters
position – The lookup position in 3D
- Returns
The field value at
position
-
virtual std::vector<double> getMax() const = 0
get the maximum value of all axes of the field map
- Returns
vector returning the maxima of all field map axes
-
virtual std::vector<double> getMin() const = 0
get the minimum value of all axes of the field map
- Returns
vector returning the minima of all field map axes
-
virtual std::vector<size_t> getNBins() const = 0
get the number of bins for all axes of the field map
- Returns
vector returning number of bins for all field map axes
-
virtual bool isInside(const Vector3 &position) const = 0
check whether given 3D position is inside look-up domain
- Parameters
position – [in] global 3D position
- Returns
trueif position is inside the defined look-up grid, otherwisefalse
-
virtual Vector3 getFieldUnchecked(const Vector3 &position) const = 0
-
template<typename Mapper_t>
class InterpolatedMaterialMap : public Acts::IVolumeMaterial - #include <Acts/Material/InterpolatedMaterialMap.hpp>
Interpolate material classification values from material values on a given grid.
This class implements a material service which is initialized by a material map defined by:
a list of material values on a regular grid in some n-Dimensional space,
a transformation of global 3D coordinates onto this n-Dimensional space.
a transformation of local n-Dimensional material coordinates into global (cartesian) 3D coordinates
The material value for a given global position is then determined by:
mapping the position onto the grid,
looking up the material classification values on the closest grid points,
doing a linear interpolation of these values.
Warning
Each classification number of the material is interpolated independently and thus does not consider any correlations that exists between these values. This might work out since the used material is already a mean of the materials in a certain bin and can therewith be treated as a collection of numbers.
- Template Parameters
G – Type of the grid
Public Functions
-
inline InterpolatedMaterialMap(Mapper_t &&mapper)
Create interpolated map.
- Parameters
mapper – [in] Material map
-
inline InterpolatedMaterialMap(Mapper_t &&mapper, BinUtility bu)
Create interpolated map.
- Parameters
mapper – [in] Material map
bu – [in]
BinUtilityfor build from
-
inline const BinUtility &binUtility() const
Return the BinUtility.
-
inline const Mapper_t &getMapper() const
Convenience method to access underlying material mapper.
- Returns
The material mapper
-
inline Material getMaterial(const Vector3 &position) const
Retrieve the interpolated material.
- Parameters
position – [in] Global 3D position
- Returns
material at given position
-
inline Material getMaterial(const Vector3 &position, Cache &cache) const
Retrieve material.
- Parameters
position – [in] Global 3D position
cache – [inout] Cache object. Contains material cell used for interpolation
- Returns
material at given position
-
inline Material getMaterialGradient(const Vector3 &position, ActsMatrix<5, 5> &derivative) const
Retrieve material value & its “gradient”.
Note
Currently the derivative is not calculated
- Parameters
position – [in] Global 3D position
derivative – [out] “Gradient” of material as (5x5) matrix
- Returns
Material
-
inline Material getMaterialGradient(const Vector3 &position, ActsMatrix<5, 5> &derivative, Cache &cache) const
Retrieve material value & its “gradient”.
Note
Currently the derivative is not calculated
Note
Cache is not used currently
- Parameters
position – [in] Global 3D position
derivative – [out] “Gradient” of material as (5x5) matrix
cache – [inout] Cache object. Contains cell used for
- Returns
Material
-
inline bool isInside(const Vector3 &position) const
Check whether given 3D position is inside look-up domain.
- Parameters
position – [in] Global 3D position
- Returns
trueif position is inside the defined map, otherwisefalse
-
inline virtual const Material material(const Vector3 &position) const override
Retrieve the binned material.
- Parameters
position – [in] Global 3D position
- Returns
Material at given position
-
inline virtual std::ostream &toStream(std::ostream &sl) const override
Output Method for std::ostream.
- Parameters
sl – The outoput stream
-
struct Cache
- #include <Acts/Material/InterpolatedMaterialMap.hpp>
Temporary storage of a certain cell to improve material access.
Public Members
-
bool initialized = false
Boolean statement if the cell is initialized.
-
std::optional<typename Mapper_t::MaterialCell> matCell
Stored material cell.
-
bool initialized = false
-
template<unsigned int DIM>
struct Intersection - #include <Acts/Utilities/Intersection.hpp>
Intersection struct used for position.
Public Types
-
using Status = IntersectionStatus
Status enum.
Public Functions
-
Intersection() = default
Default constructor.
-
inline Intersection(const ActsVector<DIM> &sinter, double slength, Status sstatus)
Constructor with arguments.
- Parameters
sinter – is the position of the intersection
slength – is the path length to the intersection
sstatus – is an enum indicating the status of the intersection
-
inline explicit operator bool() const
Bool() operator for validity checking.
-
inline bool operator<(const Intersection<DIM> &si) const
Smaller operator for sorting,.
it respects the validity of the intersection
- Parameters
si – is the intersection for testing
-
inline bool operator>(const Intersection<DIM> &si) const
Greater operator for sorting,.
it respects the validity of the intersection
- Parameters
si – is the intersection for testing
Public Members
-
ActsVector<DIM>::Scalar pathLength{std::numeric_limits<double>::infinity()}
Signed path length to the intersection (if valid)
-
ActsVector<DIM> position = ActsVector<DIM>::Zero()
Position of the intersection.
-
using Status = IntersectionStatus
-
template<typename T>
struct IsReadOnlyMultiTrajectory
-
template<>
struct IsReadOnlyMultiTrajectory<ConstVectorMultiTrajectory> : public std::true_type - #include <Acts/EventData/VectorMultiTrajectory.hpp>
-
template<>
struct IsReadOnlyMultiTrajectory<VectorMultiTrajectory> : public std::false_type - #include <Acts/EventData/VectorMultiTrajectory.hpp>
-
template<typename T>
struct IsReadOnlyTrackContainer
-
template<>
struct IsReadOnlyTrackContainer<ConstVectorTrackContainer> : public std::true_type - #include <Acts/EventData/VectorTrackContainer.hpp>
-
template<>
struct IsReadOnlyTrackContainer<VectorTrackContainer> : public std::false_type - #include <Acts/EventData/VectorTrackContainer.hpp>
-
class ISurfaceMaterial
- #include <Acts/Material/ISurfaceMaterial.hpp>
Virtual base class of surface based material description.
MaterialSlab that are associated to a surface, extended by certain special representations (binned, homogeneous)
Subclassed by Acts::BinnedSurfaceMaterial, Acts::HomogeneousSurfaceMaterial, Acts::ProtoSurfaceMaterial
Public Functions
-
ISurfaceMaterial() = default
Constructor.
-
inline ISurfaceMaterial(double splitFactor)
Constructor.
- Parameters
splitFactor – is the splitting ratio between pre/post update
-
inline ISurfaceMaterial(double splitFactor, Acts::MappingType mappingType)
Constructor.
- Parameters
splitFactor – is the splitting ratio between pre/post update
mappingType – is the type of surface mapping associated to the surface
-
virtual ~ISurfaceMaterial() = default
Destructor.
-
inline double factor(Direction pDir, MaterialUpdateStage mStage) const
Update pre factor.
- Parameters
pDir – is the positive direction through the surface
mStage – is the material update directive (onapproach, full, onleave)
-
inline MappingType mappingType() const
Return the type of surface material mapping.
-
virtual const MaterialSlab &materialSlab(const Vector2 &lp) const = 0
Return method for full material description of the Surface.
from local coordinate on the surface
- Parameters
lp – is the local position used for the (eventual) lookup
- Returns
const MaterialSlab
-
inline MaterialSlab materialSlab(const Vector2 &lp, Direction pDir, MaterialUpdateStage mStage) const
Return method for fully scaled material description of the Surface.
from local coordinate on the surface
- Parameters
lp – is the local position used for the (eventual) lookup
pDir – is the positive direction through the surface
mStage – is the material update directive (onapproach, full, onleave)
- Returns
MaterialSlab
-
virtual const MaterialSlab &materialSlab(const Vector3 &gp) const = 0
Return method for full material description of the Surface.
from the global coordinates
- Parameters
gp – is the global position used for the (eventual) lookup
- Returns
const MaterialSlab
-
inline MaterialSlab materialSlab(const Vector3 &gp, Direction pDir, MaterialUpdateStage mStage) const
Return method for full material description of the Surface.
from the global coordinates
- Parameters
gp – is the global position used for the (eventual) lookup
pDir – is the positive direction through the surface
mStage – is the material update directive (onapproach, full, onleave)
- Returns
MaterialSlab
-
virtual const MaterialSlab &materialSlab(size_t bin0, size_t bin1) const = 0
Direct access via bins to the MaterialSlab.
- Parameters
bin0 – is the material bin in dimension 0
bin1 – is the material bin in dimension 1
-
virtual ISurfaceMaterial &operator*=(double scale) = 0
Scale operator.
- Parameters
scale – is the scale factor applied
-
virtual std::ostream &toStream(std::ostream &sl) const = 0
Output Method for std::ostream, to be overloaded by child classes.
Friends
-
inline friend std::ostream &operator<<(std::ostream &out, const ISurfaceMaterial &sm)
output stream operator
Prints information about this object to the output stream using the virtual ISurfaceMaterial::toStream method
- Returns
modified output stream object
-
ISurfaceMaterial() = default
-
template<typename vfitter_t, typename sfinder_t>
class IterativeVertexFinder - #include <Acts/Vertexing/IterativeVertexFinder.hpp>
Implements an iterative vertex finder.
Brief description of the algorithm implemented: Iterative vertex finder which iteratively finds and fits vertices:
A list of seed tracks (
seedTracks, which is the same as the input track list to the finder at the very first iteration) is used to retrieve a single vertex seed using the ZScanVertexFinder.All tracks compatible with the current vertex seed are kept and used for fitting the single vertex. 3.1 If the vertex is a ‘good’ vertex (i.e. meets requirements) and no track reassignment after first fit is required, go to step 4. If vertex is not a good vertex, remove all tracks in perigeesToFit from seedTracks. 3.2 If vertex meets requirements and track reassignment after first fit is required, iterate over all previously found vertices (“old vertex”) and over all their tracksAtVertex. Compare compatibility of each track with old vertex and current vertex. If track is more compatible with current vertex, remove track from old vertex, put track back to perigeesToFit and refit current vertex with additional track.
If good vertex,
removeUsedCompatibleTracksmethod is called, which removes all used tracks that are compatible with the fitted vertex fromperigeesToFitandseedTracks. It also removes outliers tracks from tracksAtVertex if not compatible.Add vertex to vertexCollection
Repeat until no seedTracks are left or max. number of vertices found
- Template Parameters
vfitter_t – Vertex fitter type
sfinder_t – Seed finder type
Public Types
-
using InputTrack_t = typename vfitter_t::InputTrack_t
-
using IPEstimator = ImpactPointEstimator<InputTrack_t, Propagator_t>
Public Functions
-
inline IterativeVertexFinder(Config &cfg, std::function<BoundTrackParameters(InputTrack_t)> func, std::unique_ptr<const Logger> logger = getDefaultLogger("IterativeVertexFinder", Logging::INFO))
Constructor for user-defined InputTrack_t type =! BoundTrackParameters.
- Parameters
cfg – Configuration object
func – Function extracting BoundTrackParameters from InputTrack_t object
logger – The logging instance
-
template<typename T = InputTrack_t, std::enable_if_t<std::is_same<T, BoundTrackParameters>::value, int> = 0>
inline IterativeVertexFinder(Config &cfg, std::unique_ptr<const Logger> logger = getDefaultLogger("IterativeVertexFinder", Logging::INFO)) Constructor used if InputTrack_t type == BoundTrackParameters.
- Parameters
cfg – Configuration object
logger – The logging instance
-
Result<std::vector<Vertex<InputTrack_t>>> find(const std::vector<const InputTrack_t*> &trackVector, const VertexingOptions<InputTrack_t> &vertexingOptions, State &state) const
Finds vertices corresponding to input trackVector.
- Parameters
trackVector – Input tracks
vertexingOptions – Vertexing options
state – State for fulfilling interfaces
- Returns
Collection of vertices found by finder
-
struct Config
- #include <Acts/Vertexing/IterativeVertexFinder.hpp>
Configuration struct.
Public Functions
-
inline Config(const vfitter_t &fitter, Linearizer_t lin, sfinder_t sfinder, const IPEstimator &est)
Config constructor.
- Parameters
fitter – Vertex fitter
lin – Track linearizer
sfinder – The seed finder
est – ImpactPointEstimator
Public Members
-
bool createSplitVertices = false
-
double cutOffTrackWeight = 0.01
-
double cutOffTrackWeightReassign = 1
If
reassignTracksAfterFirstFitis set this threshold will be used to decide if a track should be checked for reassignment to other vertices.
-
bool doMaxTracksCut = false
-
IPEstimator ipEst
ImpactPointEstimator.
-
Linearizer_t linearizer
Linearized track factory.
-
double maximumChi2cutForSeeding = 36.
-
int maxTracks = 5000
-
int maxVertices = 50
-
bool reassignTracksAfterFirstFit = false
-
sfinder_t seedFinder
Vertex seed finder.
-
double significanceCutSeeding = 10
-
int splitVerticesTrkInvFraction = 2
-
vfitter_t vertexFitter
Vertex fitter.
-
inline Config(const vfitter_t &fitter, Linearizer_t lin, sfinder_t sfinder, const IPEstimator &est)
-
struct State
- #include <Acts/Vertexing/IterativeVertexFinder.hpp>
State struct.
Public Functions
-
inline State(const MagneticFieldProvider &field, const Acts::MagneticFieldContext &magContext)
Public Members
-
vfitter_t::State fitterState
The fitter state.
-
IPEstimator::State ipState
The IP estimator state.
-
Linearizer_t::State linearizerState
The inearizer state.
-
inline State(const MagneticFieldProvider &field, const Acts::MagneticFieldContext &magContext)
-
class ITGeoDetectorElementSplitter
- #include <Acts/Plugins/TGeo/ITGeoDetectorElementSplitter.hpp>
ITGeoElementSplitter.
Interface class that allows to define splitting of TGeoElements into sub-elements
Subclassed by Acts::TGeoCylinderDiscSplitter
Public Functions
-
virtual ~ITGeoDetectorElementSplitter() = default
Take a geometry context and TGeoElement and split it into sub elements.
Note
If no split is performed the unsplit detector element is returned
- Parameters
gctx – is a geometry context object
tgde – is a TGeoDetectorElement that is eventually split
- Returns
a vector of TGeoDetectorElement objects
-
virtual ~ITGeoDetectorElementSplitter() = default
-
class ITGeoIdentifierProvider
- #include <Acts/Plugins/TGeo/ITGeoIdentifierProvider.hpp>
ITGeoIdentierProvider.
Interface class that provides an Identifier from a TGeoNode
Public Functions
-
virtual Identifier identify(const GeometryContext &gctx, const TGeoNode &tgnode) const = 0
Take a geometry context and a TGeoNode and provide an identifier.
- Parameters
gctx – is a geometry context object
tgnode – is a TGeoNode that is translated
-
virtual Identifier identify(const GeometryContext &gctx, const TGeoNode &tgnode) const = 0
-
class ITrackingGeometryBuilder
- #include <Acts/Geometry/ITrackingGeometryBuilder.hpp>
Interface class for the TrackingGeometry building, this is used by the TrackingGeometrySvc to build the geometry.
The TrackingGeometry is written to the detector store and thus not created as a std::shared_ptr.
The TrackingGeometry is returned as a non-const object in order to recreate from conditions callback if necessary.
Subclassed by Acts::KDTreeTrackingGeometryBuilder, Acts::TrackingGeometryBuilder
Public Functions
-
virtual ~ITrackingGeometryBuilder() = default
Virtual destructor.
-
virtual std::unique_ptr<const TrackingGeometry> trackingGeometry(const GeometryContext &gctx) const = 0
TrackingGeometry Interface method.
- Parameters
gctx – is the geometry context for witch the geometry is built
- Returns
unique pointer to a newly created TrackingGeometry
-
virtual ~ITrackingGeometryBuilder() = default
-
class ITrackingGeometryJsonDecorator
- #include <Acts/Plugins/Json/ITrackingGeometryJsonDecorator.hpp>
helper class to add extra information to surface or volume json objects
Public Functions
-
virtual ~ITrackingGeometryJsonDecorator() = default
-
virtual void decorate(const Acts::Surface &surface, nlohmann::json &json) const = 0
Add extra elements to the json object already filled for the given surface.
- Parameters
surface – the surface which was used to fill the json object
json – the json object that is enhanced
-
virtual void decorate(const Acts::TrackingVolume &volume, nlohmann::json &json) const = 0
Add extra elements to the json object already filled for the given volume.
- Parameters
volume – the volume which was used to fill the json object
json – the json object that is enhanced
-
virtual ~ITrackingGeometryJsonDecorator() = default
-
class ITrackingVolumeArrayCreator
- #include <Acts/Geometry/ITrackingVolumeArrayCreator.hpp>
Interface class ITrackingVolumeArrayCreators It inherits from IAlgTool.
It is designed to centralize the code to create Arrays of Tracking Volumes for both:
confinement in another TrackingVolume
navigation and glueing
Arrays for glueing and confinement are often the same, therefore the newly created TrackingVolumeArray is done by a shared_ptr
Subclassed by Acts::TrackingVolumeArrayCreator
Public Functions
-
virtual ~ITrackingVolumeArrayCreator() = default
Virtual destructor.
-
virtual std::shared_ptr<const TrackingVolumeArray> trackingVolumeArray(const GeometryContext &gctx, const TrackingVolumeVector &vols, BinningValue bVal) const = 0
TrackingVolumeArrayCreator interface method - creates array depending on the binning type.
- Parameters
gctx – [in] the geometry context for this building
vols – are the TrackingVolumes ordered in a tracker
bVal – is the binning value for the volume binning
- Returns
sahred pointer to a new TrackingVolumeArray
-
class ITrackingVolumeBuilder
- #include <Acts/Geometry/ITrackingVolumeBuilder.hpp>
Interface class ITrackingVolumeBuilders.
this returns the sub-detector tracking volume that is wrapped by the next outer one in the TrackingGeometry building process
If an innerVolume is given, this is wrapped If a VolumeBounds object is given this defines the maximum extent.
Subclassed by Acts::CuboidVolumeBuilder, Acts::CylinderVolumeBuilder
Public Functions
-
virtual ~ITrackingVolumeBuilder() = default
Virtual destructor.
-
virtual MutableTrackingVolumePtr trackingVolume(const GeometryContext &gctx, TrackingVolumePtr oppositeVolume = nullptr, VolumeBoundsPtr outsideBounds = nullptr) const = 0
ITrackingVolumeBuilder interface method.
- Parameters
gctx – is the geometry context for witch the volume is built
oppositeVolume – is an (optional) volume to be wrapped
outsideBounds – is an (optional) outside confinement
- Returns
shared pointer to a newly created TrackingVolume
-
virtual ~ITrackingVolumeBuilder() = default
-
class ITrackingVolumeHelper
- #include <Acts/Geometry/ITrackingVolumeHelper.hpp>
Interface class ITrackingVolumeHelper tools, it inherits from IAlgTool.
The ITrackingVolumeHelper is a tool to pack a set of layers into a volume, or - to wrap several volumes into a container volume.
TrackingVolumes only exist as std::shared_ptr
Subclassed by Acts::CylinderVolumeHelper
Public Functions
-
virtual ~ITrackingVolumeHelper() = default
Virtual destructor.
-
virtual MutableTrackingVolumePtr createContainerTrackingVolume(const GeometryContext &gctx, const TrackingVolumeVector &volumes) const = 0
Create a one level higher TrackingVolue.
- Parameters
gctx – is the geometry context for witch the volume is built
volumes – the volumes to be contained
- Returns
shared pointer to a new TrackingVolume
Create a gap volume from dimensions and.
- Parameters
gctx – is the geometry context for witch the volume is built
mtvVector – Vector of confined TrackingVolumes
volumeMaterial – material properties for this TrackingVolume
loc0Min, loc0Max, loc1Min, loc1Max – local position in space,
layerPositions – custom layer positions
cylinder – type of layers
volumeName – : volume name to be given
btype – (optional) BinningType - arbitrary(default) or equidistant
- Returns
shared pointer to a new TrackingVolume
Create a gap volume from dimensions and.
- Parameters
gctx – is the geometry context for witch the volume is built
mtvVector – Vector of confined TrackingVolumes
volumeMaterial – material properties for this TrackingVolume
loc0Min, loc0Max, loc1Min, loc1Max – : local position in space, this TrackingVolume is restricted to Translation only
materialLayers – number of material layers (equidistant binning)
cylinder – type of layers
volumeName – volume name to be given
- Returns
shared pointer to a new TrackingVolume
Create a TrackingVolume* from a set of layers and (optional) parameters.
- Parameters
gctx – is the geometry context for witch the volume is built
layers – vector of static layers confined by the TrackingVolume if no bounds or HepTransform is given, they define the size together with the volume enevlope parameters
volumeMaterial – material properties for this TrackingVolume
mtvVector – Vector of confined TrackingVolumes
loc0Min, loc0Max, loc1Min, loc1Max – : local position in space, this TrackingVolume is restricted to Translation only
volumeName – volume name to be given
btype – (optional) BinningType - arbitrary(default) or equidistant
- Returns
shared pointer to a new TrackingVolume
Create a TrackingVolume* from a set of layers and (optional) parameters.
- Parameters
gctx – is the geometry context for witch the volume is built
layers – vector of static layers confined by the TrackingVolume if no bounds or HepTransform is given, they define the size together with the volume enevlope parameters
volumeMaterial – material properties for this TrackingVolume
volumeBounds – confinement of this TrackingVolume
mtvVector – (optional) Vector of confined TrackingVolumes
transform – (optional) placement of this TrackingVolume
volumeName – volume name to be given
btype – (optional) BinningType - arbitrary(default) or equidistant
- Returns
shared pointer to a new TrackingVolume
-
virtual ~ITrackingVolumeHelper() = default
-
class IVisualization3D
- #include <Acts/Visualization/IVisualization3D.hpp>
Partially abstract base class which provides an interface to visualization helper classes.
It provides a number of methods that all the helpers need to conform to.
Subclassed by Acts::ObjVisualization3D< T >, Acts::PlyVisualization3D< T >
Public Types
-
using FaceType = std::vector<size_t>
Public Functions
-
virtual void clear() = 0
Remove all contents of this helper.
-
virtual void face(const std::vector<Vector3> &vtxs, ColorRGB color = {120, 120, 120}) = 0
Draw a face that connects a list of vertices.
Note
Depending on the helper implementation, out of plane vertices might be handled differently.
- Parameters
vtxs – The vertices that make up the face
color – The color of the face
-
virtual void faces(const std::vector<Vector3> &vtxs, const std::vector<FaceType> &faces, ColorRGB color = {120, 120, 120}) = 0
Draw a faces that connects a list of vertices - expert only.
Note
Depending on the helper implementation, out of plane vertices might be handled differently.
- Parameters
vtxs – The vertices that make up the faceS
faces – The face presectiotions (i.e. connecting vertices)
color – The color of the face
-
virtual void line(const Vector3 &a, const Vector3 &b, ColorRGB color = {120, 120, 120}) = 0
Draw a line from a vertex to another.
- Parameters
a – The start vertex
b – The end vertex
color – The color of the line
-
virtual void vertex(const Vector3 &vtx, ColorRGB color = {120, 120, 120}) = 0
Draw a vertex at a given location and a color.
- Parameters
vtx – The vertex position
color – The color
-
virtual void write(const std::string &path) const = 0
Write the content of the helper to an outstream.
Note
will change to std::filesystem::path once gcc9 is standard
- Parameters
path – is the file system path for writing the file
-
virtual void write(std::ostream &os) const = 0
Write the content of the helper to an outstream.
- Parameters
os – The output stream for file
-
using FaceType = std::vector<size_t>
-
class IVolumeMaterial
- #include <Acts/Material/IVolumeMaterial.hpp>
Material associated with a Volume (homogeneous, binned, interpolated)
Virtual base class of volume material description.
Subclassed by Acts::HomogeneousVolumeMaterial, Acts::InterpolatedMaterialMap< Mapper_t >, Acts::ProtoVolumeMaterial
Public Functions
-
virtual ~IVolumeMaterial() = default
Virtual Destructor.
-
virtual const Material material(const Vector3 &position) const = 0
Access to actual material.
- Parameters
position – is the request position for the material call
-
virtual std::ostream &toStream(std::ostream &sl) const = 0
Output Method for std::ostream, to be overloaded by child classes.
Friends
-
inline friend std::ostream &operator<<(std::ostream &out, const IVolumeMaterial &vm)
output stream operator
Prints information about this object to the output stream using the virtual IVolumeeMaterial::toStream method
- Returns
modified output stream object
-
virtual ~IVolumeMaterial() = default
-
class IVolumeMaterialJsonDecorator
- #include <Acts/Plugins/Json/IVolumeMaterialJsonDecorator.hpp>
helper class to add extra information to surface or volume json objects
Public Functions
-
virtual ~IVolumeMaterialJsonDecorator() = default
-
virtual void decorate(const Acts::ISurfaceMaterial &material, nlohmann::json &json) const = 0
Add extra elements to the json object already filled for the given surface material.
- Parameters
material – the surface material which was used to fill the json object
json – the json object that is enhanced
-
virtual void decorate(const Acts::IVolumeMaterial &material, nlohmann::json &json) const = 0
Add extra elements to the json object already filled for the given volume material.
- Parameters
material – the volume material which was used to fill the json object
json – the json object that is enhanced
-
virtual ~IVolumeMaterialJsonDecorator() = default
-
struct jsonKey
- #include <Acts/Plugins/Json/GeometryJsonKeys.hpp>
store in a single place the different key used for the material mapping
Public Members
-
std::string binkey = "binUtility"
The bin key.
-
std::string datakey = "data"
The data key.
-
std::string mapkey = "mapMaterial"
The mapping key, add surface to mapping procedure if true.
-
std::string maptype = "mappingType"
The mapping type key, used to select the type od material mapping for the surface.
-
std::string materialkey = "material"
The material key.
-
std::string namekey = "NAME"
The name identification.
-
std::string transfokeys = "transformation"
The local to global transformation key.
-
std::string typekey = "type"
The type key -> proto, else.
-
std::string binkey = "binUtility"
-
class JsonMaterialDecorator : public Acts::IMaterialDecorator
- #include <Acts/Plugins/Json/JsonMaterialDecorator.hpp>
Material decorator from Json format.
This reads in material maps for surfaces and volumes from a json file
Public Types
-
using SurfaceMaterialMap = std::map<GeometryIdentifier, std::shared_ptr<const ISurfaceMaterial>>
-
using VolumeMaterialMap = std::map<GeometryIdentifier, std::shared_ptr<const IVolumeMaterial>>
Public Functions
-
JsonMaterialDecorator(const MaterialMapJsonConverter::Config &rConfig, const std::string &jFileName, Acts::Logging::Level level, bool clearSurfaceMaterial = true, bool clearVolumeMaterial = true)
-
virtual void decorate(Surface &surface) const final
Decorate a surface.
- Parameters
surface – the non-cost surface that is decorated
-
virtual void decorate(TrackingVolume &volume) const final
Decorate a TrackingVolume.
- Parameters
volume – the non-cost volume that is decorated
-
using SurfaceMaterialMap = std::map<GeometryIdentifier, std::shared_ptr<const ISurfaceMaterial>>
-
template<typename propagator_t, typename traj_t>
class KalmanFitter - #include <Acts/TrackFitting/KalmanFitter.hpp>
Kalman fitter implementation.
The Kalman filter contains an Actor and a Sequencer sub-class. The Sequencer has to be part of the Navigator of the Propagator in order to initialize and provide the measurement surfaces.
The Actor is part of the Propagation call and does the Kalman update and eventually the smoothing. Updater, Smoother and Calibrator are given to the Actor for further use:
The Updater is the implemented kalman updater formalism, it runs via a visitor pattern through the measurements.
The Smoother is called at the end of the filtering by the Actor.
Measurements are not required to be ordered for the KalmanFilter, measurement ordering needs to be figured out by the navigation of the propagator.
The void components are provided mainly for unit testing.
- Template Parameters
propagator_t – Type of the propagation class
Public Functions
-
inline KalmanFitter(propagator_t pPropagator, std::unique_ptr<const Logger> _logger = getDefaultLogger("KalmanFitter", Logging::INFO))
-
template<typename source_link_iterator_t, typename start_parameters_t, typename parameters_t = BoundTrackParameters, typename track_container_t, template<typename> class holder_t, bool _isdn = isDirectNavigator>
inline auto fit(source_link_iterator_t it, source_link_iterator_t end, const start_parameters_t &sParameters, const KalmanFitterOptions<traj_t> &kfOptions, const std::vector<const Surface*> &sSequence, TrackContainer<track_container_t, traj_t, holder_t> &trackContainer) const -> std::enable_if_t<_isdn, Result<typename TrackContainer<track_container_t, traj_t, holder_t>::TrackProxy>> Fit implementation of the forward filter, calls the the filter and smoother/reversed filter.
Note
The input measurements are given in the form of
SourceLinks. It’scalibrator_t'sjob to turn them into calibrated measurements used in the fit.- Template Parameters
source_link_iterator_t – Iterator type used to pass source links
start_parameters_t – Type of the initial parameters
parameters_t – Type of parameters used for local parameters
track_container_t – Type of the track container backend
holder_t – Type defining track container backend ownership
- Parameters
it – Begin iterator for the fittable uncalibrated measurements
end – End iterator for the fittable uncalibrated measurements
sParameters – The initial track parameters
kfOptions – KalmanOptions steering the fit
sSequence – surface sequence used to initialize a DirectNavigator
trackContainer – Input track container storage to append into
- Returns
the output as an output track
-
template<typename source_link_iterator_t, typename start_parameters_t, typename parameters_t = BoundTrackParameters, typename track_container_t, template<typename> class holder_t, bool _isdn = isDirectNavigator>
inline auto fit(source_link_iterator_t it, source_link_iterator_t end, const start_parameters_t &sParameters, const KalmanFitterOptions<traj_t> &kfOptions, TrackContainer<track_container_t, traj_t, holder_t> &trackContainer) const -> std::enable_if_t<!_isdn, Result<typename TrackContainer<track_container_t, traj_t, holder_t>::TrackProxy>> Fit implementation of the forward filter, calls the the filter and smoother/reversed filter.
Note
The input measurements are given in the form of
SourceLinks. It’s the calibrators job to turn them into calibrated measurements used in the fit.- Template Parameters
source_link_iterator_t – Iterator type used to pass source links
start_parameters_t – Type of the initial parameters
parameters_t – Type of parameters used for local parameters
track_container_t – Type of the track container backend
holder_t – Type defining track container backend ownership
- Parameters
it – Begin iterator for the fittable uncalibrated measurements
end – End iterator for the fittable uncalibrated measurements
sParameters – The initial track parameters
kfOptions – KalmanOptions steering the fit
trackContainer – Input track container storage to append into
- Returns
the output as an output track
-
template<typename traj_t>
struct KalmanFitterExtensions - #include <Acts/TrackFitting/KalmanFitter.hpp>
Extension struct which holeds delegates to customize the KF behavior.
Public Types
-
using Calibrator = Delegate<void(const GeometryContext&, const CalibrationContext&, const SourceLink&, TrackStateProxy)>
-
using ConstTrackStateProxy = typename traj_t::ConstTrackStateProxy
-
using OutlierFinder = Delegate<bool(ConstTrackStateProxy)>
-
using Parameters = typename TrackStateProxy::Parameters
-
using ReverseFilteringLogic = Delegate<bool(ConstTrackStateProxy)>
-
using Smoother = Delegate<Result<void>(const GeometryContext&, traj_t&, size_t, const Logger&)>
-
using TrackStateProxy = typename traj_t::TrackStateProxy
-
using Updater = Delegate<Result<void>(const GeometryContext&, TrackStateProxy, Direction, const Logger&)>
Public Functions
-
inline KalmanFitterExtensions()
Default constructor which connects the default void components.
Public Members
-
Calibrator calibrator
The Calibrator is a dedicated calibration algorithm that allows to calibrate measurements using track information, this could be e.g.
sagging for wires, module deformations, etc.
-
OutlierFinder outlierFinder
Determines whether a measurement is supposed to be considered as an outlier.
-
ReverseFilteringLogic reverseFilteringLogic
Decides whether the smoothing stage uses linearized transport or full reverse propagation.
-
Smoother smoother
The smoother back-propagates measurement information along the track.
-
SourceLinkSurfaceAccessor surfaceAccessor
Retrieves the associated surface from a source link.
-
Updater updater
The updater incorporates measurement information into the track parameters.
-
using Calibrator = Delegate<void(const GeometryContext&, const CalibrationContext&, const SourceLink&, TrackStateProxy)>
-
template<typename traj_t>
struct KalmanFitterOptions - #include <Acts/TrackFitting/KalmanFitter.hpp>
Combined options for the Kalman fitter.
- Template Parameters
traj_t – The trajectory type
Public Functions
-
KalmanFitterOptions() = delete
Contexts are required and the options must not be default-constructible.
-
inline KalmanFitterOptions(const GeometryContext &gctx, const MagneticFieldContext &mctx, std::reference_wrapper<const CalibrationContext> cctx, KalmanFitterExtensions<traj_t> extensions_, const PropagatorPlainOptions &pOptions, const Surface *rSurface = nullptr, bool mScattering = true, bool eLoss = true, bool rFiltering = false, double rfScaling = 1.0, const FreeToBoundCorrection &freeToBoundCorrection_ = FreeToBoundCorrection(false))
PropagatorOptions with context.
- Parameters
gctx – The goemetry context for this fit
mctx – The magnetic context for this fit
cctx – The calibration context for this fit
extensions_ – The KF extensions
pOptions – The plain propagator options
rSurface – The reference surface for the fit to be expressed at
mScattering – Whether to include multiple scattering
eLoss – Whether to include energy loss
rFiltering – Whether to run filtering in reversed direction as smoothing
rfScaling – Scale factor for the covariance matrix before the backward filtering
freeToBoundCorrection_ – Correction for non-linearity effect during transform from free to bound
Public Members
-
std::reference_wrapper<const CalibrationContext> calibrationContext
context object for the calibration
-
bool energyLoss = true
Whether to consider energy loss.
-
KalmanFitterExtensions<traj_t> extensions
-
FreeToBoundCorrection freeToBoundCorrection
Whether to include non-linear correction during global to local transformation.
-
std::reference_wrapper<const GeometryContext> geoContext
Context object for the geometry.
-
std::reference_wrapper<const MagneticFieldContext> magFieldContext
Context object for the magnetic field.
-
bool multipleScattering = true
Whether to consider multiple scattering.
-
PropagatorPlainOptions propagatorPlainOptions
The trivial propagator options.
-
const Surface *referenceSurface = nullptr
The reference Surface.
-
bool reversedFiltering = false
Whether to run filtering in reversed direction overwrite the ReverseFilteringLogic.
-
double reversedFilteringCovarianceScaling = 1.0
Factor by which the covariance of the input of the reversed filtering is scaled.
This is only used in the backwardfiltering (if reversedFiltering is true or if the ReverseFilteringLogic return true for the track of interest)
-
template<typename traj_t>
struct KalmanFitterResult - #include <Acts/TrackFitting/KalmanFitter.hpp>
Public Members
-
bool finished = false
-
std::optional<BoundTrackParameters> fittedParameters
-
traj_t *fittedStates = {nullptr}
-
size_t lastMeasurementIndex = SIZE_MAX
-
size_t lastTrackIndex = SIZE_MAX
-
size_t measurementHoles = 0
-
size_t measurementStates = 0
-
std::vector<const Surface*> missedActiveSurfaces
-
std::vector<const Surface*> passedAgainSurfaces
-
size_t processedStates = 0
-
bool reversed = false
-
bool smoothed = false
-
bool finished = false
-
template<std::size_t Dims, typename Type, typename Scalar = double, template<typename, std::size_t> typename Vector = std::array, std::size_t LeafSize = 4>
class KDTree - #include <Acts/Utilities/KDTree.hpp>
A general k-d tree with fast range search.
This is a generalized k-d tree, with a configurable number of dimension, scalar type, content type, index type, vector type, and leaf size. This class is purposefully generalized to support a wide range of use cases.
A k-d tree is, in essence, a k-dimensional binary search tree. Each internal node splits the content of the tree in half, with the pivot point being an orthogonal hyperplane in one of the k dimensions. This allows us to efficiently look up points within certain k-dimensional ranges.
This particular class is mostly a wrapper class around an underlying node class which does all the actual work.
Note
This type is completely immutable after construction.
- Template Parameters
Dims – The number of dimensions.
Type – The type of value contained in the tree.
Scalar – The scalar type used to construct position vectors.
Vector – The general vector type used to construct coordinates.
LeafSize – The maximum number of elements stored in a leaf node.
Public Types
-
using const_iterator_t = typename vector_t::const_iterator
-
using iterator_t = typename vector_t::iterator
The type of iterators in our vectors.
-
using pair_t = std::pair<coordinate_t, Type>
The type of coordinate-value pairs.
-
using range_t = RangeXD<Dims, Scalar, Vector>
The type describing a multi-dimensional orthogonal range.
-
using value_t = Type
The type of value contained in this k-d tree.
-
using vector_t = std::vector<pair_t>
The type of a vector of coordinate-value pairs.
Public Functions
-
KDTree() = delete
-
inline KDTree(vector_t &&d)
Construct a k-d tree from a vector of position-value pairs.
This constructor takes an r-value reference to a vector of position-value pairs and constructs a k-d tree from those pairs.
- Parameters
d – The vector of position-value pairs to construct the k-d tree from.
-
inline const_iterator_t begin(void) const
-
inline const_iterator_t end(void) const
-
inline std::vector<Type> rangeSearch(const range_t &r) const
Perform an orthogonal range search within the k-d tree.
A range search operation is one that takes a k-d tree and an orthogonal range, and returns all values associated with coordinates in the k-d tree that lie within the orthogonal range. k-d trees can do this operation quickly.
- Parameters
r – The range to search for.
- Returns
The vector of all values that lie within the given range.
-
inline void rangeSearch(const range_t &r, std::vector<Type> &v) const
Perform an in-place orthogonal range search within the k-d tree.
This range search module operates in place, writing its results to the given output vector.
- Parameters
r – The range to search for.
v – The vector to write the output to.
-
template<typename OutputIt>
inline void rangeSearchInserter(const range_t &r, OutputIt i) const Perform an orthogonal range search within the k-d tree, writing the resulting values to an output iterator.
This method allows the user more control in where the result is written to.
- Template Parameters
OutputIt – The type of the output iterator.
- Parameters
r – The range to search for.
i – The iterator to write the output to.
-
template<typename OutputIt>
inline void rangeSearchInserterWithKey(const range_t &r, OutputIt i) const Perform an orthogonal range search within the k-d tree, writing the resulting values to an output iterator, including the keys.
Performs the same operation as the keyless version, but includes the key in the output.
- Template Parameters
OutputIt – The type of the output iterator.
- Parameters
r – The range to search for.
i – The iterator to write the output to.
-
template<typename Result>
inline std::vector<Result> rangeSearchMap(const range_t &r, std::function<Result(const coordinate_t&, const Type&)> f) const Perform an orthogonal range search within the k-d tree, applying a mapping function to the values found.
In some cases, we may wish to transform the values in some way. This method allows the user to provide a mapping function which takes a set of coordinates and a value and transforms them to a new value, which is returned.
Note
Your compiler may not be able to deduce the result type automatically, in which case you will need to specify it manually.
- Template Parameters
Result – The return type of the map operation.
- Parameters
r – The range to search for.
f – The mapping function to apply to key-value pairs.
- Returns
A vector of elements matching the range after the application of the mapping function.
-
template<typename Callable>
inline void rangeSearchMapDiscard(const range_t &r, Callable &&f) const Perform an orthogonal range search within the k-d tree, applying a a void-returning function with side-effects to each key-value pair.
This is the most general version of range search in this class, and every other operation can be reduced to this operation as long as we allow arbitrary side-effects.
Functional programmers will know this method as mapM_.
- Parameters
r – The range to search for.
f – The mapping function to apply to key-value pairs.
-
template<typename Result, typename OutputIt>
inline void rangeSearchMapInserter(const range_t &r, std::function<Result(const coordinate_t&, const Type&)> f, OutputIt i) const Perform an orthogonal range search within the k-d tree, applying a mapping function to the values found, and inserting them into an inserter.
Performs the same operation as the interter-less version, but allows the user additional control over the insertion process.
Note
Your compiler may not be able to deduce the result type automatically, in which case you will need to specify it manually.
- Template Parameters
Result – The return type of the map operation.
OutputIt – The type of the output iterator.
- Parameters
r – The range to search for.
f – The mapping function to apply to key-value pairs.
i – The inserter to insert the results into.
-
inline std::vector<pair_t> rangeSearchWithKey(const range_t &r) const
Perform an orthogonal range search within the k-d tree, returning keys as well as values.
Performs the same logic as the keyless version, but includes a copy of the key with each element.
- Parameters
r – The range to search for.
- Returns
The vector of all key-value pairs that lie within the given range.
-
inline void rangeSearchWithKey(const range_t &r, std::vector<pair_t> &v) const
Perform an in-place orthogonal range search within the k-d tree, including keys in the result.
Performs the same operation as the keyless version, but includes the keys in the results.
- Parameters
r – The range to search for.
v – The vector to write the output to.
-
inline std::size_t size(void) const
Return the number of elements in the k-d tree.
We simply defer this method to the root node of the k-d tree.
- Returns
The number of elements in the k-d tree.
-
class KDTreeTrackingGeometryBuilder : public Acts::ITrackingGeometryBuilder
- #include <Acts/Geometry/KDTreeTrackingGeometryBuilder.hpp>
A Tracking Geometry builder restricted to cylindrical geometries.
It takes some helper tools and a vector of surface objects, together with a ProtoDetector description that is used to query a KDTree for contained surfaces in structures defined by the proto volume.
Public Types
-
using SurfaceKDT = KDTree<2u, std::shared_ptr<Surface>, ActsScalar, std::array, 100>
Public Functions
-
KDTreeTrackingGeometryBuilder(const Config &cfg, std::unique_ptr<const Logger> logger = getDefaultLogger("KDTreeTrackingGeometryBuilder", Logging::INFO))
Constructor.
- Parameters
cfg – [in] is the configuration struct for this builder
logger – [in] logging instance
-
virtual std::unique_ptr<const TrackingGeometry> trackingGeometry(const GeometryContext &gctx) const final
TrackingGeometry Interface method.
- Parameters
gctx – geometry context of that building call
- Returns
a unique pointer to a TrackingGeometry
-
struct Config
- #include <Acts/Geometry/KDTreeTrackingGeometryBuilder.hpp>
Nested Configuration for this TrackingGeometryBuilder.
Public Members
-
std::shared_ptr<const GeometryIdentifierHook> geometryIdentifierHook = std::make_shared<GeometryIdentifierHook>()
Optional geometry identifier hook to be used during closure.
-
std::string hierarchyIndent = " "
For screen output.
-
std::shared_ptr<const LayerCreator> layerCreator = nullptr
The layer creator - for sensitives.
-
ProtoDetector protoDetector
The proto tracking geometry description.
-
std::vector<std::shared_ptr<Surface>> surfaces = {}
The created surfaces.
-
std::shared_ptr<const ITrackingVolumeHelper> trackingVolumeHelper = nullptr
The tracking volume helper for detector construction.
-
std::shared_ptr<const GeometryIdentifierHook> geometryIdentifierHook = std::make_shared<GeometryIdentifierHook>()
-
using SurfaceKDT = KDTree<2u, std::shared_ptr<Surface>, ActsScalar, std::array, 100>
-
class Layer : public virtual Acts::GeometryObject
- #include <Acts/Geometry/Layer.hpp>
Base Class for a Detector Layer in the Tracking Geometry.
An actual implemented Detector Layer inheriting from this base class has to inherit from a specific type of Surface as well. In addition, a Layer can carry:
A SurfaceArray of Surfaces holding the actual detector elements or subSurfaces. A pointer to the TrackingVolume (can only be set by such) An active/passive code : 0 - active 1 - passive [….] - other
The search type for compatible surfaces on a layer is [ the higher the number, the faster ]: ——— Layer internal ———————————————— -1 - provide all intersection tested without boundary check 0 - provide all intersection tested with boundary check 1 - provide overlap descriptor based without boundary check 2 - provide overlap descriptor based with boundary check
A layer can have substructure regarding:
m_ssRepresentingSurface -> always exists (1), can have material (2)
m_ssSensitiveSurfaces -> can or not exist (0,1), can have material (2)
m_ssApproachSurfaces -> can or not exist (0,1) cam have material (2)
Subclassed by Acts::ConeLayer, Acts::CylinderLayer, Acts::DiscLayer, Acts::NavigationLayer, Acts::PlaneLayer
Public Functions
-
Layer() = delete
Default Constructor - deleted.
-
Layer(const Layer&) = delete
Copy Constructor - deleted.
-
virtual ~Layer() = default
Destructor.
-
ApproachDescriptor *approachDescriptor()
Non-const version of the approach descriptor.
-
const ApproachDescriptor *approachDescriptor() const
Return method for the approach descriptor, can be nullptr.
Decompose Layer into (compatible) surfaces.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – Position parameter for searching
direction – Direction of the parameters for searching
options – The navigation options
- Returns
list of intersection of surfaces on the layer
-
virtual bool isOnLayer(const GeometryContext &gctx, const Vector3 &position, const BoundaryCheck &bcheck = true) const
geometrical isOnLayer() method
Note
using isOnSurface() with Layer specific tolerance
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the global position to be checked
bcheck – is the boundary check directive
- Returns
boolean that indicates success of the operation
-
LayerType layerType() const
return the LayerType
-
const Layer *nextLayer(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const
Fast navigation to next layer.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the start position for the search
direction – is the direction for the search
- Returns
the pointer to the next layer
-
Layer &operator=(const Layer &layer) = delete
Assignment operator - forbidden, layer assignment must not be ambiguous.
- Parameters
layer – is the source layer for assignment
-
const AbstractVolume *representingVolume() const
Return the abstract volume that represents the layer.
- Returns
the representing volume of the layer
-
virtual bool resolve(bool resolveSensitive, bool resolveMaterial, bool resolvePassive) const
Accept layer according to the following collection directives.
- Parameters
resolveSensitive – is the prescription to find the sensitive surfaces
resolveMaterial – is the precription to find material surfaces
resolvePassive – is the prescription to find all passive surfaces
- Returns
a boolean whether the layer is accepted for processing
-
template<typename options_t>
inline bool resolve(const options_t &options) const Accept layer according to the following collection directives.
- Template Parameters
options_t – Type of the options for navigation
- Returns
a boolean whether the layer is accepted for processing
-
SurfaceArray *surfaceArray()
Non-const version.
-
const SurfaceArray *surfaceArray() const
Return the entire SurfaceArray, returns a nullptr if no SurfaceArray.
Surface seen on approach for layers without sub structure, this is the surfaceRepresentation for layers with sub structure, this is the approachSurface.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – Position for searching
direction – Direction for searching
options – The navigation options
- Returns
the Surface intersection of the approach surface
-
virtual const Surface &surfaceRepresentation() const = 0
Transforms the layer into a Surface representation for extrapolation.
Note
the layer can be hosting many surfaces, but this is the global one to which one can extrapolate
-
virtual Surface &surfaceRepresentation() = 0
-
double thickness() const
Return the Thickness of the Layer this is by definition along the normal vector of the surfaceRepresentation.
-
const TrackingVolume *trackingVolume() const
Get the confining TrackingVolume.
- Returns
the pointer to the enclosing volume
-
class LayerArrayCreator : public Acts::ILayerArrayCreator
- #include <Acts/Geometry/LayerArrayCreator.hpp>
The LayerArrayCreator is a simple Tool that helps to construct LayerArrays from std::vector of Acts::CylinderLayer, Acts::DiscLayer, Acts::PlaneLayer.
It fills the gaps automatically with Acts::NavigationLayer to be processed easily in the Navigation of the Extrapolation process.
Public Functions
-
inline LayerArrayCreator(const Config&, std::unique_ptr<const Logger> logger = getDefaultLogger("LayerArrayCreator", Logging::INFO))
Constructor.
- Parameters
logger – logging instance
-
~LayerArrayCreator() override = default
Destructor.
-
virtual std::unique_ptr<const LayerArray> layerArray(const GeometryContext &gctx, const LayerVector &layersInput, double min, double max, BinningType bType = arbitrary, BinningValue bValue = binX) const override
LayerArrayCreator interface method.
- Parameters
gctx – is the geometry context for witch the array is built
layersInput – are the layers to be moved into an array
min – is the minimum value for binning
max – is the maximum value for binning
bType – is the binning type
bValue – is the value in which the binning should be done
- Returns
unique pointer to a newly created LayerArray
-
inline void setLogger(std::unique_ptr<const Logger> logger)
set logging instance
-
struct Config
- #include <Acts/Geometry/LayerArrayCreator.hpp>
This struct stores the configuration of the tracking geometry.
-
inline LayerArrayCreator(const Config&, std::unique_ptr<const Logger> logger = getDefaultLogger("LayerArrayCreator", Logging::INFO))
-
class LayerCreator
- #include <Acts/Geometry/LayerCreator.hpp>
The LayerCreator is able to build cylinde,r disc layers or plane layers from detector elements.
Public Functions
-
LayerCreator(const Config &lcConfig, std::unique_ptr<const Logger> logger = getDefaultLogger("LayerCreator", Logging::INFO))
Constructor.
- Parameters
lcConfig – is the configuration object
logger – logging instance
-
~LayerCreator() = default
Destructor.
-
void associateSurfacesToLayer(Layer &layer) const
returning a cylindrical layer
- Parameters
gctx – is the geometry context with which the geometry is built
surfaces – is the vector of pointers to sensitive surfaces represented by this layer
bTypePhi – binning type in phi (equidistant/arbitrary)
bTypeZ – binning type in z (equidistant/arbitrary)
_protoLayer – (optional) proto layer specifying the dimensions and envelopes
transform – is the (optional) transform of the layer
ad – possibility to hand over a specific ApproachDescriptor, which is needed for material mapping. Otherwise the default ApproachDescriptor will be taken used for this layer
- Pre
the pointers to the sensitive surfaces in the surfaces vectors all need to be valid, since no check is performed
- Returns
shared pointer to a newly created layer
returning a cylindrical layer
- Parameters
gctx – is the geometry context with which the geometry is built
surfaces – is the vector of pointers to sensitive surfaces represented by this layer
binsPhi – is number of bins the sensitive surfaces are ordered in phi
binsZ – is number of bins the sensitive surfaces are ordered in Z
_protoLayer – (optional) proto layer specifying the dimensions and envelopes
transform – is the (optional) transform of the layer
ad – possibility to hand over a specific ApproachDescriptor, which is needed for material mapping. Otherwise the default ApproachDescriptor will be taken used for this layer
- Pre
the pointers to the sensitive surfaces in the surfaces vectors all need to be valid, since no check is performed
- Returns
shared pointer to a newly created layer
returning a disc layer
- Parameters
gctx – is the geometry context with which the geometry is built
surfaces – is the vector of pointers to sensitive surfaces represented by this layer
bTypeR – binning type in r (equidistant/arbitrary)
bTypePhi – binning type in phi (equidistant/arbitrary)
transform – is the (optional) transform of the layer
_protoLayer – (optional) proto layer specifying the dimensions and envelopes
ad – possibility to hand over a specific ApproachDescriptor, which is needed for material mapping. Otherwise the default ApproachDescriptor will be taken used for this layer
- Pre
the pointers to the sensitive surfaces in the surfaces vectors all need to be valid, since no check is performed
- Returns
shared pointer to a newly created layer
returning a disc layer
- Parameters
gctx – is the geometry context with which the geometry is built
surfaces – is the vector of pointers to sensitive surfaces represented by this layer
binsR – is number of bins the sensitive surfaces are ordered in R
binsPhi – is number of bins the sensitive surfaces are ordered in Phi
transform – is the (optional) transform of the layer
_protoLayer – (optional) proto layer specifying the dimensions and envelopes
ad – possibility to hand over a specific ApproachDescriptor, which is needed for material mapping. Otherwise the default ApproachDescriptor will be taken used for this layer
- Pre
the pointers to the sensitive surfaces in the surfaces vectors all need to be valid, since no check is performed
- Returns
shared pointer to a newly created layer
-
inline Config getConfiguration() const
Access th configuration object.
returning a plane layer
- Parameters
gctx – is the geometry context with which the geometry is built
surfaces – [in] is the vector of pointers to sensitive surfaces represented by this layer
bins1 – [in] is the number of bins in the orthogonal direction to
bValuebins2 – [in] is the number of bins in the orthogonal direction to
bValuebValue – [in] Direction of the aligned surfaces
transform – [in] is the (optional) transform of the layer
_protoLayer – [in] (optional) proto layer specifying the dimensions and envelopes
ad – [in] possibility to hand over a specific ApproachDescriptor, which is needed for material mapping. Otherwise the default ApproachDescriptor will be taken used for this layer
- Pre
the pointers to the sensitive surfaces in the surfaces vectors all need to be valid, since no check is performed
- Returns
shared pointer to a newly created layer
-
void setConfiguration(const Config &lcConfig)
Set the configuration object.
- Parameters
lcConfig – is the configuration struct
-
void setLogger(std::unique_ptr<const Logger> newLogger)
set logging instance
- Parameters
newLogger – the logger instance
-
struct Config
- #include <Acts/Geometry/LayerCreator.hpp>
Configuration for the LayerCreator This is the nexted configuration struct for the LayerCreator class.
Public Functions
-
Config() = default
standard constructor
Public Members
-
double cylinderPhiTolerance = {0.1}
cylinder module phi tolerance : it counts at same phi, if …
-
double cylinderZtolerance = {10.}
cylinder module z tolerance : it counts at same z, if …
-
std::shared_ptr<const SurfaceArrayCreator> surfaceArrayCreator = nullptr
surface array helper
-
Config() = default
-
LayerCreator(const Config &lcConfig, std::unique_ptr<const Logger> logger = getDefaultLogger("LayerCreator", Logging::INFO))
-
struct LinCircle
- #include <Acts/Seeding/SeedFinderUtils.hpp>
A partial description of a circle in u-v space.
Public Functions
-
LinCircle() = default
-
inline LinCircle(float ct, float idr, float er, float u, float v, float X, float Y)
Public Members
-
float cotTheta = {0.}
-
float Er = {0.}
-
float iDeltaR = {0.}
-
float U = {0.}
-
float V = {0.}
-
float x = {0.}
-
float y = {0.}
-
LinCircle() = default
-
class LinearizedTrack
- #include <Acts/Vertexing/LinearizedTrack.hpp>
Class for linear expansion of track parameters in vicinity of vertex.
The measurement equation is linearized in the following way:
F_k= D_k (x_k - x_0k) + E_k (p_k - p_0k) + F^0_k
where F_k are the parameters at perigee nearest to the linearization point, x_k is the position of the vertex, p_k the track momentum at the vertex, and F^0_k is the constant term of expansion. D_k and E_k are matrices of derivatives, denoted hereafter as “positionJacobian” and “momentumJacobian” respectively.
Public Functions
-
LinearizedTrack() = default
-
inline LinearizedTrack(const BoundVector ¶msAtPCA, const BoundSquareMatrix &parCovarianceAtPCA, const BoundSquareMatrix &parWeightAtPCA, const Vector4 &linPoint, const ActsMatrix<eBoundSize, 4> &posJacobian, const ActsMatrix<eBoundSize, 3> &momJacobian, const Vector4 &position, const Vector3 &momentum, const BoundVector &constTerm)
Constructor taking perigee parameters and covariance matrix of track propagated to closest approach (PCA) of linearization point, position and momentum Jacobian and const term.
- Parameters
paramsAtPCA – Parameters at point of closest approach
parCovarianceAtPCA – Parameter covariance matrix at point of closest approach
parWeightAtPCA – The weight at the point of closest approach
linPoint – Linearization point
posJacobian – Position jacobian
momJacobian – Momentum jacobian
position – Position at point of closest approach
momentum – Momentum at point of closest approach
constTerm – Constant term in taylor expansion
Public Members
-
BoundVector constantTerm = {BoundVector::Zero()}
-
BoundSquareMatrix covarianceAtPCA = {BoundSquareMatrix::Zero()}
-
ActsMatrix<eBoundSize, 3> momentumJacobian = {ActsMatrix<eBoundSize, 3>::Zero()}
-
BoundVector parametersAtPCA = {BoundVector::Zero()}
-
ActsMatrix<eBoundSize, 4> positionJacobian = {ActsMatrix<eBoundSize, 4>::Zero()}
-
BoundSquareMatrix weightAtPCA = {BoundSquareMatrix::Zero()}
-
LinearizedTrack() = default
-
class LineBounds : public Acts::SurfaceBounds
- #include <Acts/Surfaces/LineBounds.hpp>
Bounds for a LineSurface.
Public Types
-
enum BoundValues
Values:
-
enumerator eR
-
enumerator eHalfLengthZ
-
enumerator eSize
-
enumerator eR
Public Functions
-
LineBounds() = delete
-
inline LineBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor - from fixed size array.
- Parameters
values – The parameter values
-
inline LineBounds(double r, double halfZ) noexcept(false)
Constructor.
- Parameters
r – is the radius of the cylinder, default = 0.
halfZ – is the half length in z, default = 0.
-
~LineBounds() override = default
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck) const final
Inside check for the bounds object driven by the boundary check directive Each Bounds has a method inside, which checks if a LocalPosition is inside the bounds Inside can be called without/with tolerances.
- Parameters
lposition – Local position (assumed to be in right surface frame)
bcheck – boundary check directive
- Returns
boolean indicator for the success of this operation
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
- Parameters
sl – is the ostream to be dumped into
-
virtual BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
enum BoundValues
-
class LineSurface : public Acts::Surface
- #include <Acts/Surfaces/LineSurface.hpp>
Base class for a linear surfaces in the TrackingGeometry to describe dirft tube, straw like detectors or the Perigee It inherits from Surface.
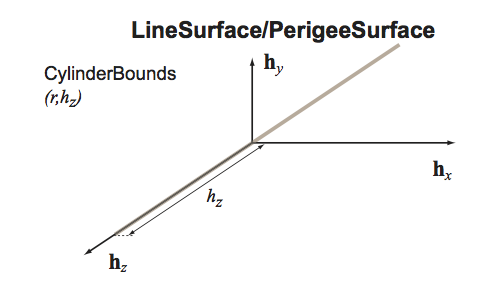
Note
It leaves the type() method virtual, so it can not be instantiated
Subclassed by Acts::PerigeeSurface, Acts::StrawSurface
Public Functions
-
LineSurface() = delete
-
~LineSurface() override = default
-
virtual AlignmentToPathMatrix alignmentToPathDerivative(const GeometryContext &gctx, const FreeVector ¶meters) const final
Calculate the derivative of path length at the geometry constraint or point-of-closest-approach w.r.t.
alignment parameters of the surface (i.e. local frame origin in global 3D Cartesian coordinates and its rotation represented with extrinsic Euler angles)
- Parameters
gctx – The current geometry context object, e.g. alignment
parameters – is the free parameters
- Returns
Derivative of path length w.r.t. the alignment parameters
-
virtual Vector3 binningPosition(const GeometryContext &gctx, BinningValue bValue) const final
The binning position is the position calculated for a certain binning type.
- Parameters
gctx – The current geometry context object, e.g. alignment
bValue – is the binning type to be used
- Returns
position that can beused for this binning
-
virtual const SurfaceBounds &bounds() const final
This method returns the bounds of the surface by reference.
-
virtual BoundToFreeMatrix boundToFreeJacobian(const GeometryContext &gctx, const BoundVector &boundParams) const final
Calculate the jacobian from local to global which the surface knows best, hence the calculation is done here.
- Parameters
gctx – The current geometry context object, e.g. alignment
boundParams – is the bound parameters vector
- Returns
Jacobian from local to global
-
virtual FreeToPathMatrix freeToPathDerivative(const GeometryContext &gctx, const FreeVector ¶meters) const final
Calculate the derivative of path length at the geometry constraint or point-of-closest-approach w.r.t.
free parameters
- Parameters
gctx – The current geometry context object, e.g. alignment
parameters – is the free parameters
- Returns
Derivative of path length w.r.t. free parameters
-
virtual Result<Vector2> globalToLocal(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, double tolerance = s_onSurfaceTolerance) const final
Specified for
LineSurface: global to local method without dynamic memory allocation.This method is the true global -> local transformation. It makes use of
globalToLocaland indicates the sign of theActs::eBoundLoc0by the given momentum direction.The calculation of the sign of the radius (or \( d_0 \)) can be done as follows: May \( \vec d = \vec m - \vec c \) denote the difference between the center of the line and the global position of the measurement/predicted state. Then, \( \vec d \) lies in the so-called measurement plane. The latter is determined by the two orthogonal vectors \( \vec{\texttt{measY}} = \vec{e}_z \) and \( \vec{\texttt{measX}} = \vec{\texttt{measY}} \times \frac{\vec{p}}{|\vec{p}|} \).
The sign of the radius (or \( d_{0} \) ) is then defined by the projection of \( \vec{d} \) on \( \vec{measX} \):\( sign = -sign(\vec{d} \cdot \vec{measX}) \)
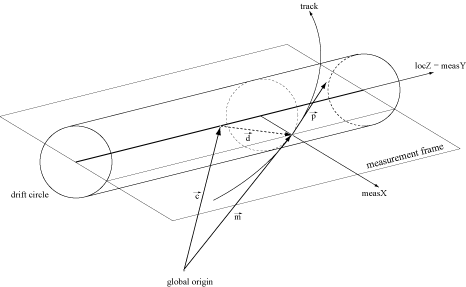
- Parameters
gctx – The current geometry context object, e.g. alignment
position – global 3D position - considered to be on surface but not inside bounds (check is done)
direction – global 3D momentum direction (optionally ignored)
tolerance – (unused)
- Returns
A
Result<Vector2>, which is set to!ok()if thepositionis not the point of closest approach to the line surface.
-
virtual SurfaceIntersection intersect(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck = false, ActsScalar tolerance = s_onSurfaceTolerance) const final
Calculate the straight-line intersection with the line surface.
Mathematical motivation:
Given two lines in parameteric form:
\( \vec l_{a}(u) = \vec m_a + u \cdot \vec e_{a} \)
\( \vec l_{b}(\mu) = \vec m_b + \mu \cdot \vec e_{b} \)
The vector between any two points on the two lines is given by:
\( \vec s(u, \mu) = \vec l_{b} - l_{a} = \vec m_{ab} + \mu \cdot \vec e_{b} - u \cdot \vec e_{a} \),
where \( \vec m_{ab} = \vec m_{b} - \vec m_{a} \).
\( \vec s(u_0, \mu_0) \) denotes the vector between the two closest points
\( \vec l_{a,0} = l_{a}(u_0) \) and \( \vec l_{b,0} = l_{b}(\mu_0) \)
and is perpendicular to both, \( \vec e_{a} \) and \( \vec e_{b} \).
This results in a system of two linear equations:
(i) \( 0 = \vec s(u_0, \mu_0) \cdot \vec e_a = \vec m_{ab} \cdot \vec e_a + \mu_0 \vec e_a \cdot \vec e_b - u_0 \)
(ii) \( 0 = \vec s(u_0, \mu_0) \cdot \vec e_b = \vec m_{ab} \cdot \vec e_b + \mu_0 - u_0 \vec e_b \cdot \vec e_a \)
Solving (i) and (ii) for \( u \) and \( \mu_0 \) yields:
\( u_0 = \frac{(\vec m_{ab} \cdot \vec e_a)-(\vec m_{ab} \cdot \vec e_b)(\vec e_a \cdot \vec e_b)}{1-(\vec e_a \cdot \vec e_b)^2} \)
\( \mu_0 = - \frac{(\vec m_{ab} \cdot \vec e_b)-(\vec m_{ab} \cdot \vec e_a)(\vec e_a \cdot \vec e_b)}{1-(\vec e_a \cdot \vec e_b)^2} \)
The function checks if \( u_0 \simeq 0\) to check if the current
positionis at the point of closest approach, i.e. the intersection point, in which case it will return anonSuraceintersection result. Otherwise, the path length frompositionto the point of closest approach ( \( u_0 \)) is returned in areachableintersection.Note
expected to be normalized
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The global position as a starting point
direction – The global direction at the starting point
bcheck – The boundary check directive for the estimate
tolerance – the tolerance used for the intersection
- Returns
is the intersection object
-
Vector3 lineDirection(const GeometryContext &gctx) const
-
virtual ActsMatrix<2, 3> localCartesianToBoundLocalDerivative(const GeometryContext &gctx, const Vector3 &position) const final
Calculate the derivative of bound track parameters local position w.r.t.
position in local 3D Cartesian coordinates
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The position of the parameters in global
- Returns
Derivative of bound local position w.r.t. position in local 3D cartesian coordinates
-
virtual Vector3 localToGlobal(const GeometryContext &gctx, const Vector2 &lposition, const Vector3 &direction) const final
Local to global transformation.
Note
for line surfaces the momentum direction is used in order to interpret the drift radius
- Parameters
gctx – The current geometry context object, e.g. alignment
lposition – is the local position to be transformed
direction – is the global momentum direction (used to sign the closest approach)
- Returns
global position by value
-
virtual std::string name() const override
Return properly formatted class name for screen output.
-
inline Vector3 normal(const GeometryContext &gctx) const
Normal vector return without argument.
-
virtual Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const final
The normal vector is undefined if we do not know the momentum.
- Parameters
gctx – The current geometry context object, e.g. alignment
lposition – is the local position is ignored
- Returns
a zero vector
-
Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const = 0
Normal vector return without argument.
-
Vector3 normal(const GeometryContext &gctx, const Vector3 &position) const
Normal vector return without argument.
-
LineSurface &operator=(const LineSurface &other)
Assignment operator.
- Parameters
other – is the source surface dor copying
-
virtual double pathCorrection(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const override
the pathCorrection for derived classes with thickness is by definition 1 for LineSurfaces
Note
input parameters are ignored
Note
there’s no material associated to the line surface
-
virtual RotationMatrix3 referenceFrame(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const final
Return the measurement frame - this is needed for alignment, in particular.
for StraightLine and Perigee Surface
the default implementation is the RotationMatrix3 of the transform
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the global position where the measurement frame is constructed
direction – is the momentum direction used for the measurement frame construction
- Returns
is a rotation matrix that indicates the measurement frame
-
LineSurface() = delete
-
class Logger
- #include <Acts/Utilities/Logger.hpp>
class for printing debug output
This class provides the user interface for printing debug messages with different levels of severity.
Public Functions
-
inline Logger(std::unique_ptr<Logging::OutputPrintPolicy> pPrint, std::unique_ptr<Logging::OutputFilterPolicy> pFilter)
construct from output print and filter policy
- Parameters
pPrint – [in] policy for printing debug messages
pFilter – [in] policy for filtering debug messages
-
inline std::unique_ptr<Logger> clone(const std::optional<std::string> &_name = std::nullopt, const std::optional<Logging::Level> &_level = std::nullopt) const
Make a copy of this logger, optionally changing the name or the level.
- Parameters
_name – the optional new name
_level – the optional new level
-
inline std::unique_ptr<Logger> clone(Logging::Level _level) const
Make a copy of the logger, with a new level.
Convenience function for if you only want to change the level but not the name.
- Parameters
_level – the new level
- Returns
the new logger
-
inline std::unique_ptr<Logger> cloneWithSuffix(const std::string &suffix, std::optional<Logging::Level> _level = std::nullopt) const
Make a copy of the logger, with a suffix added to the end of it’s name.
You can also optionally supply a new level
- Parameters
suffix – the suffix to add to the end of the name
_level – the optional new level
-
inline bool doPrint(const Logging::Level &lvl) const
decide whether a message with a given debug level has to be printed
- Parameters
lvl – [in] debug level of debug message
- Returns
trueif debug message should be printed, otherwisefalse
-
inline const Logging::OutputFilterPolicy &filterPolicy() const
Return the filter policy for this logger.
- Returns
the filter policy
-
inline Logging::Level level() const
Return the level of the filter policy of this logger.
- Returns
the level
-
inline void log(const Logging::Level &lvl, const std::string &input) const
log a debug message
- Parameters
lvl – [in] debug level of debug message
input – [in] text of debug message
-
inline const std::string &name() const
Return the name of the print policy of this logger.
- Returns
the name
-
inline const Logger &operator()() const
Helper function so a logger reference can be used as is with the logging macros.
-
inline const Logging::OutputPrintPolicy &printPolicy() const
Return the print policy for this logger.
- Returns
the print policy
-
inline Logger(std::unique_ptr<Logging::OutputPrintPolicy> pPrint, std::unique_ptr<Logging::OutputFilterPolicy> pFilter)
-
class MagneticFieldProvider
- #include <Acts/MagneticField/MagneticFieldProvider.hpp>
Base class for all magnetic field providers.
Subclassed by Acts::ConstantBField, Acts::InterpolatedMagneticField, Acts::NullBField, Acts::SolenoidBField
Public Types
-
using Cache = detail::SmallObjectCache
Opaque cache type that can store arbitrary implementation specific cache data.
Examples are an interpolation cell, or an experiment specific conditions data handle.
Public Functions
-
inline virtual ~MagneticFieldProvider()
-
virtual Result<Vector3> getField(const Vector3 &position, Cache &cache) const = 0
Retrieve magnetic field value at a given location.
Requires a cache object created through makeCache().
- Parameters
position – [in] global 3D position for the lookup
cache – [inout] Field provider specific cache object
- Returns
magnetic field vector at given position
-
virtual Result<Vector3> getFieldGradient(const Vector3 &position, ActsMatrix<3, 3> &derivative, Cache &cache) const = 0
Retrieve magnetic field value its its gradient.
Requires a cache object created through makeCache().
- Parameters
position – [in] global 3D position
derivative – [out] gradient of magnetic field vector as (3x3) matrix
cache – [inout] Field provider specific cache object
- Returns
magnetic field vector
-
virtual Cache makeCache(const MagneticFieldContext &mctx) const = 0
Make an opaque cache for the magnetic field.
Instructs the specific implementation to generate a
Cacheinstance for magnetic field lookup.- Parameters
mctx – The magnetic field context to generate cache for
- Returns
Cache The opaque cache object
-
using Cache = detail::SmallObjectCache
-
class Material
- #include <Acts/Material/Material.hpp>
Material description for interactions with matter.
The following parameters are used to specify the material and its interactions with traversing particles:
radiation length X0 (native length units)
nuclear interaction length L0 (native length units)
relative atomic mass Ar (unitless number)
nuclear charge number Z (elementary charge e)
molar density (native amount-of-substance unit / (native length unit)³)
The parameters can be effective or average parameters e.g. when a mixture of materials is described.
Note
Always use the opaque parameters vector to serialize/deserialize the material information. Since the internal storage might be different from the external accessors, this ensures that always the numerically optimal parameters are stored. Use the
ParametersVectortype and do not assume any particular size since we might consider to store more parameters in the future.Public Types
-
using ParametersVector = Eigen::Matrix<float, 5, 1>
Public Functions
-
Material() = default
Construct a vacuum representation.
-
Material(const Material &mat) = default
-
Material(const ParametersVector ¶meters)
Construct from an encoded parameters vector.
-
Material(Material &&mat) = default
-
~Material() = default
-
inline constexpr float Ar() const
Return the relative atomic mass.
-
inline constexpr float L0() const
Return the nuclear interaction length. Infinity in case of vacuum.
-
float massDensity() const
Return the mass density.
-
float meanExcitationEnergy() const
Return the mean electron excitation energy.
-
inline constexpr float molarDensity() const
Return the molar density.
-
inline constexpr float molarElectronDensity() const
Return the molar electron density.
-
inline constexpr operator bool() const
Check if the material is valid, i.e. it is not vacuum.
-
ParametersVector parameters() const
Encode the properties into an opaque parameters vector.
-
inline constexpr float X0() const
Return the radition length. Infinity in case of vacuum.
-
inline constexpr float Z() const
Return the nuclear charge number.
Public Static Functions
-
static Material fromMassDensity(float x0, float l0, float ar, float z, float massRho)
Construct from material parameters using the mass density.
Warning
Due to the choice of native mass units, using the mass density can lead to numerical problems. Typical mass densities lead to computations with values differing by 20+ orders of magnitude.
- Parameters
x0 – is the radiation length
l0 – is the nuclear interaction length
ar – is the relative atomic mass
z – is the nuclear charge number
massRho – is the mass density
-
static Material fromMolarDensity(float x0, float l0, float ar, float z, float molarRho)
Construct from material parameters using the molar density.
- Parameters
x0 – is the radiation length
l0 – is the nuclear interaction length
ar – is the relative atomic mass
z – is the nuclear charge number
molarRho – is the molar density
-
struct MaterialCollector
- #include <Acts/Material/MaterialCollector.hpp>
A Material Collector struct.
Public Types
-
using result_type = this_result
Public Functions
Collector action for the ActionList of the Propagator It checks if the state has a current surface, in which case the action is performed:
it records the surface given the configuration
- Template Parameters
propagator_state_t – is the type of Propagator state
stepper_t – Type of the stepper of the propagation
navigator_t – Type of the navigator of the propagation
- Parameters
state – is the mutable propagator state object
stepper – The stepper in use
navigator – The navigator in use
result – is the result object to be filled
logger – a logger instance
Public Members
-
bool detailedCollection = false
In the detailed collection mode the material per surface is collected, otherwise only the total pathlength in X0 or L0 are recorded.
-
struct this_result
- #include <Acts/Material/MaterialCollector.hpp>
Simple result struct to be returned.
Result of the material collection process It collects the overall X0 and L0 path lengths, and optionally a detailed per-material breakdown
-
using result_type = this_result
-
class MaterialComposition
- #include <Acts/Material/MaterialComposition.hpp>
Material composed from multiple elements with varying factions.
See also
ElementFraction for details.
Public Functions
-
MaterialComposition() = default
Construct an empty composition corresponding to vacuum.
-
MaterialComposition(const MaterialComposition&) = default
-
MaterialComposition(MaterialComposition&&) = default
-
inline MaterialComposition(std::vector<ElementFraction> elements)
Constructor from element fractions.
Rescales the fractions so they all add up to unity within the accuracy.
-
~MaterialComposition() = default
-
inline auto begin() const
-
inline auto end() const
-
inline operator bool() const
Check if the composed material is valid, i.e. it is not vacuum.
-
MaterialComposition &operator=(const MaterialComposition&) = default
-
MaterialComposition &operator=(MaterialComposition&&) = default
-
inline std::size_t size() const
Return the number of elements.
-
MaterialComposition() = default
-
struct MaterialHit
- #include <Acts/Material/MaterialCollector.hpp>
The information to be writtern out per hit surface.
-
struct MaterialInteraction
- #include <Acts/Material/MaterialInteraction.hpp>
The Material interaction struct It records the surface and the passed material This is only necessary recorded when configured.
Public Members
-
double deltaP = 0.0
The momentum change due to the interaction.
-
GeometryIdentifier intersectionID
The ID where the interaction occurred.
-
MaterialSlab materialSlab
The effective, passed material properties including the path correction.
-
double pathCorrection = 1.
The path correction factor due to non-zero incidence on the surface.
-
double sigmaPhi2 = 0.0
Expected phi variance due to the interactions.
-
double sigmaQoP2 = 0.0
Expected q/p variance due to the interactions.
-
double sigmaTheta2 = 0.0
Expected theta variance due to the interactions.
-
const Surface *surface = nullptr
The surface where the interaction occurred.
-
double time = 0.0
The particle time at the interaction.
-
bool updatedVolumeStep = false
Update the volume step to implement the proper step size.
-
const TrackingVolume *volume = nullptr
The volume where the interaction occurred.
-
double deltaP = 0.0
-
struct MaterialInteractor
- #include <Acts/Propagator/MaterialInteractor.hpp>
Material interactor propagator action.
Apply material interactions at a surface and update the track state.
Public Types
-
using result_type = RecordedMaterial
Public Functions
Interaction with detector material for the ActionList of the Propagator.
It checks if the state has a current surface, in which case the action is performed: the covariance is transported to the position, multiple scattering and energy loss is applied according to the configuration.
- Template Parameters
propagator_state_t – is the type of Propagagor state
stepper_t – Type of the stepper of the propagation
navigator_t – Type of the navigator of the propagation
- Parameters
state – is the mutable propagator state object
stepper – The stepper in use
navigator – The navigator in use
result – is the mutable result state object
logger – a logger instance
Public Members
-
bool energyLoss = true
Whether to consider energy loss.
-
bool multipleScattering = true
Whether to consider multiple scattering.
-
bool recordInteractions = false
Whether to record all material interactions.
-
using result_type = RecordedMaterial
-
class MaterialMapJsonConverter
- #include <Acts/Plugins/Json/MaterialMapJsonConverter.hpp>
read the material from Json
Public Types
-
using DetectorMaterialMaps = std::pair<SurfaceMaterialMap, VolumeMaterialMap>
-
using SurfaceMaterialMap = std::map<GeometryIdentifier, std::shared_ptr<const ISurfaceMaterial>>
-
using VolumeMaterialMap = std::map<GeometryIdentifier, std::shared_ptr<const IVolumeMaterial>>
Public Functions
-
MaterialMapJsonConverter(const Config &config, Acts::Logging::Level level)
Constructor.
- Parameters
config – configuration struct for the reader
level – The log level
-
~MaterialMapJsonConverter() = default
Destructor.
-
void convertToHierarchy(std::vector<std::pair<GeometryIdentifier, Acts::TrackingVolumeAndMaterial>> &volumeHierarchy, std::vector<std::pair<GeometryIdentifier, Acts::SurfaceAndMaterialWithContext>> &surfaceHierarchy, const Acts::TrackingVolume *tVolume)
Go through a volume to find subvolume, layers and surfaces.
Store volumes and surfaces in two vector used to initialised the geometry hierarchy.
- Parameters
volumeHierarchy – is a vector of volume to be filled
surfaceHierarchy – is a vector of surfaces to be filled
tVolume – is a volume
-
DetectorMaterialMaps jsonToMaterialMaps(const nlohmann::json &materialmaps)
Convert a json material map to a DetectorMaterialMaps.
- Parameters
materialmaps – The json material
-
nlohmann::json materialMapsToJson(const DetectorMaterialMaps &maps, const IVolumeMaterialJsonDecorator *decorator = nullptr)
Convert a DetectorMaterialMaps to json.
- Parameters
maps – The material map collection
decorator – nullptr or a decorator to add extra attributes
-
nlohmann::json trackingGeometryToJson(const TrackingGeometry &tGeometry, const ITrackingGeometryJsonDecorator *decorator = nullptr)
Convert a tracking geometry to json.
Can be used to initialise the material mapping process.
- Parameters
tGeometry – is the tracking geometry
decorator – nullptr or a decorator to add extra attributes
-
class Config
- #include <Acts/Plugins/Json/MaterialMapJsonConverter.hpp>
Configuration of the Converter.
Public Members
-
GeometryContext context = GeometryContext()
Default geometry context to extract surface transforms.
-
bool processApproaches = true
Steering to handle approach data.
-
bool processBoundaries = true
Steering to handle boundary data.
-
bool processDenseVolumes = false
Steering to handle volume data.
-
bool processNonMaterial = false
Add proto material to all surfaces.
-
bool processRepresenting = true
Steering to handle representing data.
-
bool processSensitives = true
Steering to handle sensitive data.
-
bool processVolumes = true
Steering to handle volume data.
-
GeometryContext context = GeometryContext()
-
using DetectorMaterialMaps = std::pair<SurfaceMaterialMap, VolumeMaterialMap>
-
template<typename G>
struct MaterialMapper - #include <Acts/Material/InterpolatedMaterialMap.hpp>
Struct for mapping global 3D positions to material values.
Global 3D positions are transformed into a
DIM_POSDimensional vector which is used to look up the material classification value in the underlying material map.Public Types
-
using Grid_t = G
Public Functions
-
inline MaterialMapper(std::function<ActsVector<DIM_POS>(const Vector3&)> transformPos, Grid_t grid)
Default constructor.
- Parameters
transformPos – [in] Mapping of global 3D coordinates (cartesian) onto grid space
grid – [in] Grid storing material classification values
-
inline const Grid_t &getGrid() const
Get a const reference on the underlying grid structure.
- Returns
Grid reference
-
inline Material getMaterial(const Vector3 &position) const
Retrieve interpolated material at given position.
- Parameters
position – [in] Global 3D position
- Returns
Material at the given position
- Pre
The given
positionmust lie within the range of the underlying map.
-
inline MaterialCell getMaterialCell(const Vector3 &position) const
Retrieve material cell for given position.
- Parameters
position – [in] Global 3D position
- Returns
material cell containing the given global position
- Pre
The given
positionmust lie within the range of the underlying map.
-
inline std::vector<double> getMax() const
Get the maximum value of all axes of the map.
- Returns
Vector returning the maxima of all map axes
-
inline std::vector<double> getMin() const
Get the minimum value of all axes of the map.
- Returns
Vector returning the minima of all map axes
-
inline std::vector<size_t> getNBins() const
Get the number of bins for all axes of the map.
- Returns
Vector returning number of bins for all map axes
-
inline bool isInside(const Vector3 &position) const
Check whether given 3D position is inside look-up domain.
- Parameters
position – [in] Global 3D position
- Returns
trueif position is inside the defined look-up grid, otherwisefalse
Public Static Attributes
-
static constexpr size_t DIM_POS = Grid_t::DIM
-
struct MaterialCell
- #include <Acts/Material/InterpolatedMaterialMap.hpp>
Struct representing smallest grid unit in material grid.
This type encapsulate all required information to perform linear interpolation of material classification values within a 3D volume.
Public Functions
-
inline MaterialCell(std::function<ActsVector<DIM_POS>(const Vector3&)> transformPos, std::array<double, DIM_POS> lowerLeft, std::array<double, DIM_POS> upperRight, std::array<Material::ParametersVector, N> materialValues)
Default constructor.
- Parameters
transformPos – [in] Mapping of global 3D coordinates onto grid space
lowerLeft – [in] Generalized lower-left corner of hyper box (containing the minima of the hyper box along each Dimension)
upperRight – [in] Generalized upper-right corner of hyper box (containing the maxima of the hyper box along each Dimension)
materialValues – [in] Material classification values at the hyper box corners sorted in the canonical order defined in Acts::interpolate
-
inline Material getMaterial(const Vector3 &position) const
Retrieve material at given position.
- Parameters
position – [in] Global 3D position
- Returns
Material at the given position
- Pre
The given
positionmust lie within the current cell.
-
inline bool isInside(const Vector3 &position) const
Check whether given 3D position is inside this cell.
- Parameters
position – [in] Global 3D position
- Returns
trueif position is inside the current cell, otherwisefalse
Public Static Attributes
-
static constexpr unsigned int N = 1 << DIM_POS
Number of corner points defining the confining hyper-box.
-
inline MaterialCell(std::function<ActsVector<DIM_POS>(const Vector3&)> transformPos, std::array<double, DIM_POS> lowerLeft, std::array<double, DIM_POS> upperRight, std::array<Material::ParametersVector, N> materialValues)
-
using Grid_t = G
-
class MaterialSlab
- #include <Acts/Material/MaterialSlab.hpp>
Material description for an object with defined thickness.
This is intended to describe concrete surface materials.
See also
Material for a description of the available parameters.
Public Functions
-
MaterialSlab() = default
Construct vacuum without thickness.
-
MaterialSlab(const Material &material, float thickness)
Construct from material description.
- Parameters
material – is the material description
thickness – is the thickness of the material
-
MaterialSlab(const MaterialSlab&) = default
-
MaterialSlab(const std::vector<MaterialSlab> &layers)
Construct by averaging the material properties over multiple layers.
The resulting object has the combined thickness of all layers but just one set of appropriately averaged material constants.
- Parameters
layers – Input layers to average over.
-
MaterialSlab(float thickness)
Construct vacuum with thickness.
-
MaterialSlab(MaterialSlab&&) = default
-
~MaterialSlab() = default
-
inline constexpr const Material &material() const
Access the (average) material parameters.
-
inline constexpr operator bool() const
Check if the material is valid, i.e. it is finite and not vacuum.
-
MaterialSlab &operator=(const MaterialSlab&) = default
-
MaterialSlab &operator=(MaterialSlab&&) = default
-
void scaleThickness(float scale)
Scale the material thickness by the given factor.
-
inline constexpr float thickness() const
Return the thickness.
-
inline constexpr float thicknessInL0() const
Return the nuclear interaction length fraction.
-
inline constexpr float thicknessInX0() const
Return the radiation length fraction.
-
MaterialSlab() = default
-
struct MaterialSurface
- #include <Acts/Material/SurfaceMaterialMapper.hpp>
selector for finding surface
Public Functions
-
inline bool operator()(const Surface &sf) const
-
inline bool operator()(const Surface &sf) const
-
struct MaterialVolume
- #include <Acts/Material/SurfaceMaterialMapper.hpp>
selector for finding volume
Public Functions
-
inline bool operator()(const TrackingVolume &vf) const
-
inline bool operator()(const TrackingVolume &vf) const
-
struct MaxMomentumReducerLoop
- #include <Acts/Propagator/MultiEigenStepperLoop.hpp>
Public Static Functions
-
template<typename stepper_state_t>
static inline ActsScalar absoluteMomentum(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline ActsScalar charge(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline FreeVector cov(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline Vector3 direction(const stepper_state_t &s)
-
template<typename component_range_t>
static inline const auto &maxAbsoluteMomentumIt(const component_range_t &cmps)
-
template<typename stepper_state_t>
static inline Vector3 momentum(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline FreeVector pars(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline Vector3 position(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline ActsScalar qOverP(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline ActsScalar time(const stepper_state_t &s)
-
template<typename stepper_state_t>
-
template<typename indices_t, size_t kSize>
class Measurement - #include <Acts/EventData/Measurement.hpp>
A measurement of a fixed-size subspace of the full parameters.
The measurement intentionally does not store a pointer/reference to the reference object in the geometry hierarchy, i.e. the surface or volume. The reference object can already be identified via the geometry identifier provided by the source link. Since a measurement must be anchored within the geometry hierarchy, all measurement surfaces and volumes must provide valid geometry identifiers. In all use-cases, e.g. Kalman filtering, a pointer/reference to the reference object is available before the measurement is accessed; e.g. the propagator provides the surface pointer during navigation, which is then used to lookup possible measurements.
The pointed-to geometry object would differ depending on the parameter type. This means either, that there needs to be an additional variable type or that a pointer to a base object is stored (requiring a
dynamic_castlater on). Both variants add additional complications. Since the geometry object is not required anyways (as discussed above), not storing it removes all these complications altogether.- Template Parameters
indices_t – Parameter index type, determines the full parameter space
kSize – Size of the parameter subset.
Public Types
-
using CovarianceMatrix = ActsSquareMatrix<kSize>
Matrix type for the measurement covariance.
-
using ExpansionMatrix = ActsMatrix<kFullSize, kSize>
-
using FullParametersVector = ActsVector<kFullSize>
Vector type containing all parameters in the same space.
-
using ParametersVector = ActsVector<kSize>
Vector type containing for measured parameter values.
-
using ProjectionMatrix = ActsMatrix<kSize, kFullSize>
-
using Scalar = ActsScalar
Public Functions
-
Measurement() = delete
A measurement can only be constructed with valid parameters.
-
Measurement(const Measurement&) = default
-
Measurement(Measurement&&) = default
-
template<typename parameters_t, typename covariance_t>
inline Measurement(SourceLink source, const std::array<indices_t, kSize> &indices, const Eigen::MatrixBase<parameters_t> ¶ms, const Eigen::MatrixBase<covariance_t> &cov) Construct from source link, subset indices, and measured data.
Note
The indices must be ordered and must describe/match the content of parameters and covariance.
- Template Parameters
parameters_t – Input parameters vector type
covariance_t – Input covariance matrix type
- Parameters
source – The link that connects to the underlying detector readout
indices – Which parameters are measured
params – Measured parameters values
cov – Measured parameters covariance
-
~Measurement() = default
-
inline bool contains(indices_t i) const
Check if a specific parameter is part of this measurement.
-
inline const CovarianceMatrix &covariance() const
Measured parameters covariance.
-
inline ExpansionMatrix expander() const
Expansion matrix from the measured subspace into the full space.
This is equivalent to the transpose of the projection matrix only in the case of a trivial projection matrix. While this is the case here, it is still recommended to use the expansion matrix directly in cases where it is explicitly used.
-
inline std::ostream &operator<<(std::ostream &os) const
-
Measurement &operator=(const Measurement&) = default
-
Measurement &operator=(Measurement&&) = default
-
inline const ParametersVector ¶meters() const
Measured parameters values.
-
inline ProjectionMatrix projector() const
Projection matrix from the full space into the measured subspace.
-
inline ParametersVector residuals(const FullParametersVector &reference) const
Compute residuals in the measured subspace.
This computes the difference
measured - referencetaking into account the allowed parameter ranges. Only the reference values in the measured subspace are used for the computation.- Parameters
reference – Reference parameters in the full space.
-
inline const SourceLink &sourceLink() const
Source link that connects to the underlying detector readout.
Public Static Functions
-
static inline constexpr size_t size()
Number of measured parameters.
-
class MeasurementSelector
- #include <Acts/TrackFinding/MeasurementSelector.hpp>
Measurement selection struct selecting those measurements compatible with the given track parameter against provided criteria on one surface.
The selection criteria could be allowed maximum chi2 and allowed maximum number of measurements on one surface
If there is no compatible measurement, the measurement with the minimum chi2 will be selected and the status will be tagged as an outlier
Public Types
-
using Config = Acts::GeometryHierarchyMap<MeasurementSelectorCuts>
Geometry-dependent cut configuration.
Different components on the geometry can require different cut settings. The configuration must either contain explicit settings for all geometry components that are used or contain a global default.
Public Functions
-
MeasurementSelector() = default
Default constructor.
-
inline MeasurementSelector(Config config)
Constructor with config and (non-owning) logger.
- Parameters
config – a config instance
-
template<typename traj_t>
inline Result<std::pair<typename std::vector<typename traj_t::TrackStateProxy>::iterator, typename std::vector<typename traj_t::TrackStateProxy>::iterator>> select(std::vector<typename traj_t::TrackStateProxy> &candidates, bool &isOutlier, const Logger &logger) const Function that select the measurements compatible with the given track parameter on a surface.
- Parameters
candidates – The track state candidates which already contain predicted parameters
isOutlier – The indicator for outlier or not
logger – The logger wrapper
- Returns
Pair of iterators into candidates marking the range of selected candidates
-
using Config = Acts::GeometryHierarchyMap<MeasurementSelectorCuts>
-
struct MeasurementSelectorCuts
- #include <Acts/TrackFinding/MeasurementSelector.hpp>
Selection cuts for associating measurements with predicted track parameters on a surface.
The default configuration only takes the best matching measurement without a cut on the local chi2.
Public Members
-
std::vector<double> chi2CutOff = {std::numeric_limits<double>::max()}
Maximum local chi2 contribution.
-
std::vector<double> etaBins
bins in |eta| to specify variable selections
-
std::vector<size_t> numMeasurementsCutOff = {1}
Maximum number of associated measurements on a single surface.
-
std::vector<double> chi2CutOff = {std::numeric_limits<double>::max()}
-
template<typename T, class decorator_t>
struct missing_specialization : public std::false_type - #include <Acts/Plugins/Json/GeometryHierarchyMapJsonConverter.hpp>
-
class MLTrackClassifier : public Acts::OnnxRuntimeBase
- #include </home/docs/checkouts/readthedocs.org/user_builds/acts/checkouts/v29.0.0/Plugins/Onnx/include/Acts/Plugins/Onnx/MLTrackClassifier.hpp>
Public Types
-
enum class TrackLabels
The labels for track quality.
Values:
-
enumerator eGood
-
enumerator eDuplicate
-
enumerator eFake
-
enumerator eGood
Public Functions
-
bool isDuplicate(std::vector<float> &inputFeatures, double decisionThreshProb) const
Check if the predicted track label is ‘duplicate’.
- Parameters
inputFeatures – The vector of input features for the trajectory to be classified
decisionThreshProb – The probability threshold used to predict the track label
- Returns
If the predicted track label is ‘duplicate’
-
TrackLabels predictTrackLabel(std::vector<float> &inputFeatures, double decisionThreshProb) const
Predict the track label.
- Parameters
inputFeatures – The vector of input features for the trajectory to be classified
decisionThreshProb – The probability threshold used to predict the track label
- Returns
The predicted track label of the trajectory
-
enum class TrackLabels
-
template<typename charge_t>
class MultiComponentBoundTrackParameters - #include <Acts/EventData/MultiComponentBoundTrackParameters.hpp>
This class is only a light wrapper around a surface and a vector of parameters.
Its main purpose is to provide many constructors for the underlying vector. Most accessors are generated from the GenericBoundTrackParameters equivalent and thus may be expensive
Note
This class holds shared ownership on its reference surface.
Note
The accessors for parameters, covariance, position, etc. are the weighted means of the components.
Note
If all covariances are zero, the accessor for the total covariance does return std::nullopt; TODO Add constructor from range and projector maybe?
- Template Parameters
charge_t – Helper type to interpret the particle charge/momentum
Public Types
-
using CovarianceMatrix = typename SingleParameters::CovarianceMatrix
-
using ParametersVector = typename SingleParameters::ParametersVector
-
using Scalar = typename SingleParameters::Scalar
Public Functions
-
MultiComponentBoundTrackParameters() = delete
Parameters are not default constructible due to the charge type.
-
MultiComponentBoundTrackParameters(const MultiComponentBoundTrackParameters&) = default
-
MultiComponentBoundTrackParameters(MultiComponentBoundTrackParameters&&) = default
Construct from a parameters vector on the surface and particle charge.
In principle, only the charge magnitude is needed her to allow unambiguous extraction of the absolute momentum. The particle charge is required as an input here to be consistent with the other constructors below that that also take the charge as an input. The charge sign is only used in debug builds to check for consistency with the q/p parameter.
- Parameters
surface – Reference surface the parameters are defined on
params – Bound parameters vector
q – Particle charge
cov – Bound parameters covariance matrix
Construct from a parameters vector on the surface.
This constructor is only available if there are no potential charge ambiguities, i.e. the charge type is default-constructible.
- Parameters
surface – Reference surface the parameters are defined on
params – Bound parameters vector
cov – Bound parameters covariance matrix
Construct from multiple components with charge_t.
Construct from multiple components with charge scalar q.
-
~MultiComponentBoundTrackParameters() = default
-
inline Scalar absoluteMomentum() const
Absolute momentum.
-
inline Scalar charge() const
Particle electric charge.
-
inline const auto &components() const
Access the parameters.
-
inline std::optional<CovarianceMatrix> covariance() const
Optional covariance matrix.
-
inline Vector3 direction() const
Unit direction three-vector, i.e.
the normalized momentum three-vector.
-
inline Vector4 fourPosition(const GeometryContext &geoCtx) const
Space-time position four-vector.
- Parameters
geoCtx – [in] Geometry context for the local-to-global transformation
-
inline Vector3 momentum() const
Momentum three-vector.
-
MultiComponentBoundTrackParameters &operator=(const MultiComponentBoundTrackParameters&) = default
-
MultiComponentBoundTrackParameters &operator=(MultiComponentBoundTrackParameters&&) = default
-
inline std::pair<double, SingleParameters> operator[](std::size_t i) const
Get the weight and a GenericBoundTrackParameters object for one component.
-
inline ParametersVector parameters() const
Parameters vector.
-
inline Vector3 position(const GeometryContext &geoCtx) const
Spatial position three-vector.
- Parameters
geoCtx – [in] Geometry context for the local-to-global transformation
-
inline const Surface &referenceSurface() const
Reference surface onto which the parameters are bound.
-
inline Scalar time() const
Time coordinate.
-
inline Scalar transverseMomentum() const
Transverse momentum.
-
template<typename extensionlist_t = StepperExtensionList<DefaultExtension>, typename component_reducer_t = WeightedComponentReducerLoop, typename auctioneer_t = detail::VoidAuctioneer>
class MultiEigenStepperLoop : public Acts::EigenStepper<StepperExtensionList<DefaultExtension>, detail::VoidAuctioneer> - #include <Acts/Propagator/MultiEigenStepperLoop.hpp>
Stepper based on the EigenStepper, but handles Multi-Component Tracks (e.g., for the GSF).
Internally, this only manages a vector of EigenStepper::States. This simplifies implementation, but has several drawbacks:
There are certain redundancies between the global State and the component states
The components do not share a single magnetic-field-cache
- Template Parameters
extensionlist_t – See EigenStepper for details
component_reducer_t – How to map the multi-component state to a single component
auctioneer_t – See EigenStepper for details
small_vector_size – A size-hint how much memory should be allocated by the small vector
Public Types
-
using BoundState = std::tuple<BoundTrackParameters, Jacobian, double>
-
using ConstComponentProxy = ComponentProxyBase<const typename State::Component>
A proxy struct which allows access to a single component of the multi-component state.
It has the semantics of a const reference, i.e. it requires a const reference of the single-component state it represents
-
using Covariance = BoundSquareMatrix
-
using CurvilinearState = std::tuple<CurvilinearTrackParameters, Jacobian, double>
-
using Jacobian = BoundMatrix
Jacobian, Covariance and State definitions.
-
using Reducer = component_reducer_t
The reducer type.
-
using SingleState = typename SingleStepper::State
Typedef to the State of the single component Stepper.
-
using SingleStepper = EigenStepper<extensionlist_t, auctioneer_t>
Typedef to the Single-Component Eigen Stepper.
Public Functions
Constructor from a magnetic field and a optionally provided Logger.
-
inline double absoluteMomentum(const State &state) const
Absolute momentum accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
template<typename charge_t>
inline Result<ComponentProxy> addComponent(State &state, const GenericBoundTrackParameters<charge_t> &pars, double weight) const Add a component to the Multistepper.
Note
: It is not ensured that the weights are normalized afterwards
Note
This function makes no garantuees about how new components are initialized, it is up to the caller to ensure that all components are valid in the end.
Note
The returned component-proxy is only garantueed to be valid until the component number is again modified
- Parameters
state – [inout] The stepping state (thread-local cache)
pars – [in] Parameters of the component to add
weight – [in] Weight of the component to add
-
Result<BoundState> boundState(State &state, const Surface &surface, bool transportCov = true, const FreeToBoundCorrection &freeToBoundCorrection = FreeToBoundCorrection(false)) const
Create and return the bound state at the current position.
This transports (if necessary) the covariance to the surface and creates a bound state. It does not check if the transported state is at the surface, this needs to be guaranteed by the propagator.
Note
This is done by combining the gaussian mixture on the specified surface. If the conversion to bound states of some components fails, these components are ignored unless all components fail. In this case an error code is returned.
- Parameters
state – [in] State that will be presented as
BoundStatesurface – [in] The surface to which we bind the state
transportCov – [in] Flag steering covariance transport
freeToBoundCorrection – [in] Flag steering non-linear correction during global to local correction
- Returns
A bound state:
the parameters at the surface
the stepwise jacobian towards it (from last bound)
and the path length (from start - for ordering)
-
inline double charge(const State &state) const
Charge access.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline void clearComponents(State &state) const
Reset the number of components.
- Parameters
state – [inout] The stepping state (thread-local cache)
-
inline auto componentIterable(State &state) const
Creates an iterable which can be plugged into a range-based for-loop to iterate over components.
Note
Use a for-loop with by-value semantics, since the Iterable returns a proxy internally holding a reference
-
inline auto constComponentIterable(const State &state) const
Creates an constant iterable which can be plugged into a range-based for-loop to iterate over components.
Note
Use a for-loop with by-value semantics, since the Iterable returns a proxy internally holding a reference
-
CurvilinearState curvilinearState(State &state, bool transportCov = true) const
Create and return a curvilinear state at the current position.
This transports (if necessary) the covariance to the current position and creates a curvilinear state.
Note
This is done as a simple average over the free representation and covariance of the components.
- Parameters
state – [in] State that will be presented as
CurvilinearStatetransportCov – [in] Flag steering covariance transport
- Returns
A curvilinear state:
the curvilinear parameters at given position
the stepweise jacobian towards it (from last bound)
and the path length (from start - for ordering)
-
inline Vector3 direction(const State &state) const
Momentum direction accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline Result<Vector3> getField(State &state, const Vector3 &pos) const
Get the field for the stepping, it checks first if the access is still within the Cell, and updates the cell if necessary.
Note
This uses the cache of the first component stored in the state
- Parameters
state – [inout] is the propagation state associated with the track the magnetic field cell is used (and potentially updated)
pos – [in] is the field position
-
inline double getStepSize(const State &state, ConstrainedStep::Type stype) const
Get the step size.
Note
This returns the smallest step size of all components. It uses std::abs for comparison to handle backward propagation and negative step sizes correctly.
- Parameters
state – [in] The stepping state (thread-local cache)
stype – [in] The step size type to be returned
-
template<typename charge_t>
inline State makeState(std::reference_wrapper<const GeometryContext> gctx, std::reference_wrapper<const MagneticFieldContext> mctx, const MultiComponentBoundTrackParameters<charge_t> &par, double ssize = std::numeric_limits<double>::max()) const Construct and initialize a state.
-
inline Vector3 momentum(const State &state) const
Momentum accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline std::size_t numberComponents(const State &state) const
Get the number of components.
- Parameters
state – [in,out] The stepping state (thread-local cache)
-
inline std::string outputStepSize(const State &state) const
Output the Step Size of all components into one std::string.
- Parameters
state – [in,out] The stepping state (thread-local cache)
-
inline double overstepLimit(const State &state) const
Overstep limit.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline Vector3 position(const State &state) const
Global particle position accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline double qOverP(const State &state) const
QoP access.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline void releaseStepSize(State &state) const
Release the step-size for all components.
- Parameters
state – [in,out] The stepping state (thread-local cache)
-
inline void removeMissedComponents(State &state) const
Remove missed components from the component state.
- Parameters
state – [in,out] The stepping state (thread-local cache)
-
inline void resetState(State &state, const BoundVector &boundParams, const BoundSquareMatrix &cov, const Surface &surface, const double stepSize = std::numeric_limits<double>::max()) const
Resets the state.
- Parameters
state – [inout] State of the stepper
boundParams – [in] Parameters in bound parametrisation
cov – [in] Covariance matrix
surface – [in] The reference surface of the bound parameters
stepSize – [in] Step size
-
inline void reweightComponents(State &state) const
Reweight the components.
- Parameters
state – [inout] The stepping state (thread-local cache)
-
inline void setStepSize(State &state, double stepSize, ConstrainedStep::Type stype = ConstrainedStep::actor, bool release = true) const
Set Step size - explicitly with a double.
- Parameters
state – [in,out] The stepping state (thread-local cache)
stepSize – [in] The step size value
stype – [in] The step size type to be set
release – [in] Do we release the step size?
Perform a Runge-Kutta track parameter propagation step.
The state contains the desired step size. It can be negative during backwards track propagation, and since we’re using an adaptive algorithm, it can be modified by the stepper class during propagation.
- Parameters
state – [inout] is the propagation state associated with the track parameters that are being propagated.
navigator – [in] is the navigator of the propagation
-
inline double time(const State &state) const
Time access.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline void transportCovarianceToBound(State &state, const Surface &surface, const FreeToBoundCorrection &freeToBoundCorrection = FreeToBoundCorrection(false)) const
Method for on-demand transport of the covariance to a new curvilinear frame at current position, or direction of the state.
Note
no check is done if the position is actually on the surface
- Template Parameters
surface_t – the Surface type
- Parameters
state – [inout] State of the stepper
surface – [in] is the surface to which the covariance is forwarded
freeToBoundCorrection – [in] Flag steering non-linear correction during global to local correction to
-
inline void transportCovarianceToCurvilinear(State &state) const
Method for on-demand transport of the covariance to a new curvilinear frame at current position, or direction of the state.
- Parameters
state – [inout] State of the stepper
-
template<typename object_intersection_t>
inline void updateStepSize(State &state, const object_intersection_t &oIntersection, bool release = true) const Update step size.
This method intersects the provided surface and update the navigation step estimation accordingly (hence it changes the state). It also returns the status of the intersection to trigger onSurface in case the surface is reached.
- Parameters
state – [in,out] The stepping state (thread-local cache)
oIntersection – [in] The ObjectIntersection to layer, boundary, etc
release – [in] boolean to trigger step size release
-
inline Intersection3D::Status updateSurfaceStatus(State &state, const Surface &surface, Direction navDir, const BoundaryCheck &bcheck, ActsScalar surfaceTolerance = s_onSurfaceTolerance, const Logger &logger = getDummyLogger()) const
Update surface status.
It checks the status to the reference surface & updates the step size accordingly
- Parameters
state – [inout] The stepping state (thread-local cache)
surface – [in] The surface provided
navDir – [in] The navigation direction
bcheck – [in] The boundary check for this status update
surfaceTolerance – [in] Surface tolerance used for intersection
logger – [in] A
Loggerinstance
Public Static Attributes
-
static constexpr int maxComponents = std::numeric_limits<int>::max()
How many components can this stepper manage?
-
struct ComponentProxy : public Acts::MultiEigenStepperLoop<extensionlist_t, component_reducer_t, auctioneer_t>::ComponentProxyBase<State::Component>
- #include <Acts/Propagator/MultiEigenStepperLoop.hpp>
A proxy struct which allows access to a single component of the multi-component state.
It has the semantics of a mutable reference, i.e. it requires a mutable reference of the single-component state it represents
Public Types
-
using Base = ComponentProxyBase<typename State::Component>
Public Functions
-
inline Result<BoundState> boundState(const Surface &surface, bool transportCov, const FreeToBoundCorrection &freeToBoundCorrection)
-
inline auto &cov()
-
inline const auto &cov() const
-
inline auto &derivative()
-
inline const auto &derivative() const
-
inline auto &jacobian()
-
inline const auto &jacobian() const
-
inline auto &jacToGlobal()
-
inline const auto &jacToGlobal() const
-
inline auto &jacTransport()
-
inline const auto &jacTransport() const
-
inline auto &pars()
-
inline const auto &pars() const
-
inline auto &pathAccumulated()
-
inline auto pathAccumulated() const
-
template<typename propagator_state_t>
inline auto singleState(const propagator_state_t &state) const
-
template<typename propagator_state_t>
inline auto singleState(propagator_state_t &state)
-
inline const auto &singleStepper(const MultiEigenStepperLoop &stepper) const
-
inline auto &status()
-
inline auto status() const
-
inline void update(const FreeVector &freeParams, const BoundVector &boundParams, const Covariance &covariance, const Surface &surface)
-
inline auto &weight()
-
inline auto weight() const
-
using Base = ComponentProxyBase<typename State::Component>
-
template<typename component_t>
struct ComponentProxyBase - #include <Acts/Propagator/MultiEigenStepperLoop.hpp>
A template class which contains all const member functions, that should be available both in the mutable ComponentProxy and the ConstComponentProxy.
- Template Parameters
component_t – Must be a const or mutable State::Component.
Public Functions
-
inline ComponentProxyBase(component_t &c)
-
inline const auto &cov() const
-
inline const auto &derivative() const
-
inline const auto &jacobian() const
-
inline const auto &jacToGlobal() const
-
inline const auto &jacTransport() const
-
inline const auto &pars() const
-
inline auto pathAccumulated() const
-
template<typename propagator_state_t>
inline auto singleState(const propagator_state_t &state) const
-
inline const auto &singleStepper(const MultiEigenStepperLoop &stepper) const
-
inline auto status() const
-
inline auto weight() const
Public Members
-
component_t &cmp
-
template<typename stepping_t, typename navigation_t, typename options_t, typename geoctx_t>
struct SinglePropState - #include <Acts/Propagator/MultiEigenStepperLoop.hpp>
A helper type for providinig a propagation state which can be used with functions expecting single-component steppers and states.
Public Functions
-
struct State
- #include <Acts/Propagator/MultiEigenStepperLoop.hpp>
Public Functions
-
State() = delete
No default constructor is provided.
Constructor from the initial bound track parameters.
Note
the covariance matrix is copied when needed
- Template Parameters
charge_t – Type of the bound parameter charge
- Parameters
gctx – [in] is the context object for the geometry
mctx – [in] is the context object for the magnetic field
bfield – [in] the shared magnetic filed provider
multipars – [in] The track multi-component track-parameters at start
ssize – [in] is the maximum step size
Public Members
-
SmallVector<Component> components
The components of which the state consists.
-
bool covTransport = false
-
std::reference_wrapper<const GeometryContext> geoContext
geoContext
-
std::reference_wrapper<const MagneticFieldContext> magContext
MagneticFieldContext.
-
double pathAccumulated = 0.
-
std::optional<std::size_t> stepCounterAfterFirstComponentOnSurface
Step-limit counter which limits the number of steps when one component reached a surface.
-
std::size_t steps = 0
-
struct Component
- #include <Acts/Propagator/MultiEigenStepperLoop.hpp>
The struct that stores the individual components.
-
State() = delete
-
template<typename T, std::size_t... BitsPerLevel>
class MultiIndex - #include <Acts/Utilities/MultiIndex.hpp>
A set of (hierarchical) indices bitpacked into a single value.
The underlying value is split into blocks of bits with variable size. Each block is a level within the index hierarchy and can be set and retrieved separately. The encoded MultiIndex can be ordered and compared for equality. The ordering follows the hierarchy, i.e. indices are first ordered by the highest level, then within the highest level by the second level and so on.
Public Types
-
enum [anonymous]
Values:
-
enumerator NumLevels
-
enumerator NumLevels
-
using Value = T
The type of their underlying storage value.
Public Functions
-
MultiIndex() = default
Construct a default MultiIndex with undefined values for each level.
-
MultiIndex(const MultiIndex&) = default
-
MultiIndex(MultiIndex&) = default
-
inline constexpr MultiIndex(Value encoded)
Construct a MultiIndex from an already encoded value.
-
inline constexpr Value level(std::size_t lvl) const
Get the value for the index level.
-
inline constexpr MultiIndex makeLastDescendant(std::size_t lvl) const
Create index with every level below the selected level maximized.
-
inline constexpr MultiIndex makeNextSibling(std::size_t lvl) const
Create index with the selected level increased and levels below zeroed.
-
MultiIndex &operator=(const MultiIndex&) = default
-
MultiIndex &operator=(MultiIndex&&) = default
-
inline constexpr MultiIndex &operator=(Value encoded)
Allow setting the MultiIndex from an already encoded value.
-
inline constexpr MultiIndex &set(std::size_t lvl, Value val)
Set the value of the index level.
-
inline constexpr Value value() const
Get the encoded value of all index levels.
Public Static Functions
-
static inline constexpr std::size_t bits(std::size_t lvl)
Get the number of bits for the associated level.
-
template<typename ...Us>
static inline constexpr MultiIndex Encode(Us&&... us) Construct a MultiIndex from values for multiple level.
This functionality must be implemented as a static, named constructor to avoid confusion with other constructors. If it would be implemented as a regular constructor, constructing a MultiIndex from a single encoded value and encoding only the first level would have the same signature and could not be distinguished.
-
static inline constexpr MultiIndex Zeros()
Construct a MultiIndex with all levels set to zero.
-
enum [anonymous]
-
struct MultiStepperSurfaceReached
- #include <Acts/Propagator/MultiStepperAborters.hpp>
This.
Public Functions
-
MultiStepperSurfaceReached() = default
boolean operator for abort condition without using the result
- Template Parameters
propagator_state_t – Type of the propagator state
stepper_t – Type of the stepper
navigator_t – Type of the navigator
- Parameters
state – [inout] The propagation state object
stepper – [in] Stepper used for propagation
navigator – [in] Navigator used for the propagation
logger – a logger instance
boolean operator for abort condition without using the result
- Template Parameters
propagator_state_t – Type of the propagator state
stepper_t – Type of the stepper
navigator_t – Type of the navigator
- Parameters
state – [inout] The propagation state object
stepper – [in] Stepper used for the propagation
navigator – [in] Navigator used for the propagation
targetSurface – [in] The target surface
logger – a logger instance
Public Members
-
bool averageOnSurface = true
If this is set, we are also happy if the mean of the components is on the surface.
How the averaging is performed depends on the stepper implementation
-
double averageOnSurfaceTolerance = 0.2
A configurable tolerance within which distance to the intersection we consider the surface as reached.
Has no effect if averageOnSurface is false
-
MultiStepperSurfaceReached() = default
-
template<typename derived_t>
class MultiTrajectory - #include <Acts/EventData/MultiTrajectory.hpp>
Store a trajectory of track states with multiple components.
This container supports both simple, sequential trajectories as well as combinatorial or multi-component trajectories. Each point can store a parent point such that the trajectory forms a directed, acyclic graph of sub-trajectories. From a set of endpoints, all possible sub-components can be easily identified. Some functionality is provided to simplify iterating over specific sub-components.
Public Types
-
using ConstTrackStateProxy = detail_lt::TrackStateProxy<Derived, MeasurementSizeMax, true>
-
using Derived = derived_t
-
using IndexType = typename TrackStateProxy::IndexType
-
using TrackStateProxy = detail_lt::TrackStateProxy<Derived, MeasurementSizeMax, false>
Public Functions
-
template<typename T, bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline constexpr void addColumn(const std::string &key) Add a column to the
MultiTrajectory.Note
This takes a string argument rather than a hashed string to maintain compatibility with backends.
- Template Parameters
T – Type of the column values to add
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline constexpr IndexType addTrackState(TrackStatePropMask mask = TrackStatePropMask::All, IndexType iprevious = kInvalid) Add a track state without providing explicit information.
Which components of the track state are initialized/allocated can be controlled via
mask- Parameters
mask – The bitmask that instructs which components to allocate and which to leave invalid
iprevious – index of the previous state, kInvalid if first
- Returns
Index of the newly added track state
-
template<typename F, bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline void applyBackwards(IndexType iendpoint, F &&callable) Apply a function to all previous states starting at a given endpoint.
Warning
If the trajectory contains multiple components with common points, this can have an impact on the other components.
- Parameters
iendpoint – index of the last state
callable – modifying functor to be called with each point
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline constexpr void clear() Clear the
MultiTrajectory. Leaves the underlying storage untouched.
-
inline auto &&convertToReadOnly() const
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline TrackStateProxy getTrackState(IndexType istate) Access a writable point on the trajectory by index.
- Parameters
istate – The index to access
- Returns
Read-write proxy to the stored track state
-
inline ConstTrackStateProxy getTrackState(IndexType istate) const
Access a read-only point on the trajectory by index.
- Parameters
istate – The index to access
- Returns
Read only proxy to the stored track state
-
inline constexpr bool hasColumn(HashedString key) const
Check if a column with a key
keyexists.- Parameters
key – Key to check for a column with
- Returns
True if the column exists, false if not.
-
inline constexpr IndexType size() const
Returns the number of track states contained.
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline auto trackStateRange(IndexType iendpoint) Range for the track states from
iendpointto the trajectory start.Note
Mutable version
- Parameters
iendpoint – Trajectory entry point to start from
- Returns
Iterator pair to iterate over
-
inline auto trackStateRange(IndexType iendpoint) const
Range for the track states from
iendpointto the trajectory start.Note
Const version
- Parameters
iendpoint – Trajectory entry point to start from
- Returns
Iterator pair to iterate over
Public Static Attributes
-
static constexpr IndexType kInvalid = TrackStateProxy::kInvalid
-
static constexpr unsigned int MeasurementSizeMax = MultiTrajectoryTraits::MeasurementSizeMax
-
static constexpr bool ReadOnly = IsReadOnlyMultiTrajectory<Derived>::value
Friends
- friend class detail_lt::TrackStateProxy< Derived, MeasurementSizeMax, false >
- friend class detail_lt::TrackStateProxy< Derived, MeasurementSizeMax, true >
-
using ConstTrackStateProxy = detail_lt::TrackStateProxy<Derived, MeasurementSizeMax, true>
- #include <Acts/Geometry/NavigationLayer.hpp>
Class to be used for gaps in Volumes as a navigational link.
Navigation Layers have a surface representation, but should usually never be propagated to.
Public Functions
Default Constructor - deleted.
Copy Constructor - deleted.
Destructor.
The binning position method.
- Parameters
gctx – The current geometry context object, e.g. alignment
bValue – is the value for which the binning position is requested
as default the center is given, but may be overloaded
- Returns
The return vector can be used for binning in a TrackingVolume
Geometric isOnLayer() method using isOnSurface() with Layer specific tolerance.
- Parameters
gctx – The current geometry context object, e.g. alignment
gp – is the global position for the check
bcheck – is the boundary check directive
- Returns
boolean that indicates if the position is on surface
Assignment operator - deleted.
Accept layer according to the following collection directives.
Note
navigation layers are never accepted
- Parameters
resolveSensitive – is the prescription to find the sensitive surfaces
resolveMaterial – is the precription to find material surfaces
resolvePassive – is the prescription to find all passive surfaces
- Returns
a boolean whether the layer is accepted for processing
Transforms the layer into a Surface representation for extrapolation In general, extrapolation to a surface should be avoided.
Public Static Functions
Factory Constructor - the surface representation is given by pointer (ownership passed)
- Parameters
sRepresentation – is the representation for extrapolation
thickness – is the thickness for the binning
- #include <Acts/Propagator/Navigator.hpp>
struct for the Navigation options that are forwarded to the geometry
- Template Parameters
propagator_state_t – Type of the object for navigation state
object_t – Type of the object for navigation to check against
Public Members
The boundary check directive.
object to check against: at end
External surface identifier for which the boundary check is ignored.
Force intersection with boundaries.
The overstep tolerance for this navigation step.
The maximum path limit for this navigation step.
Always look for material.
always look for passive
Always look for sensitive.
object to check against: at start
Target surface to exclude.
- #include <Acts/Propagator/Navigator.hpp>
Navigator class.
This is an Actor to be added to the ActorList in order to navigate through the static tracking geometry setup.
The current navigation stage is cached in the state struct and updated when necessary. If any surface in the extrapolation flow is hit, it is set to the propagation satate, such that other actors can deal with it. This navigation actor thus always needs to run first! It does two things: it figures out the order of volumes, layers and surfaces.
The current target surface is the surface pointed to by of the index for the surfaces, layers or volume boundaries. If a surface is found, the state.navigation.currentSurface pointer is set. This enables subsequent actors to react. Secondly, this actor uses the ordered indices to figure out which surface, layer or volume boundary is supposed to be hit next. It then sets the maximum step size to the path length found out by straight line intersection. If the state is not on surface, it also re-computes the step size, to make sure we end up at the desired surface.
Public Types
The navigation stage.
Values:
Public Functions
Constructor with configuration object.
- Parameters
cfg – The navigator configuration
_logger – a logger instance
Initialize call - start of propagation.
- Template Parameters
propagator_state_t – The state type of the propagagor
stepper_t – The type of stepper used for the propagation
- Parameters
state – [inout] is the propagation state object
stepper – [in] Stepper in use
- Returns
boolean return triggers exit to stepper
Navigator post step call, will be called in two modes.
(a) It initializes the Navigation stream if start volume is not yet defined:
initialize the volume
establish the start layer and start volume
set the current surface to the start surface
(b) It establishes the currentSurface status during the propagation flow, currentSurface can be
surfaces still to be handled within a layer
layers still to be handled within a volume
boundaries still to be handled to exit a volume
- Template Parameters
propagator_state_t – is the type of Propagatgor state
stepper_t – is the used type of the Stepper by the Propagator
- Parameters
state – [inout] is the mutable propagator state object
stepper – [in] Stepper in use
Navigator pre step call.
Call options (a) there are still surfaces to be resolved: handle those (b) there no surfaces but still layers to be resolved, handle those (c) there are no surfaces nor layers to be resolved, handle boundary
- Template Parameters
propagator_state_t – is the type of Propagatgor state
stepper_t – is the used type of the Stepper by the Propagator
- Parameters
state – [inout] is the mutable propagator state object
stepper – [in] Stepper in use
Reset state.
- Parameters
state – is the state
geoContext – is the geometry context
pos – is the global position
dir – is the direction of navigation
ssurface – is the new starting surface
tsurface – is the target surface
- #include <Acts/Propagator/Navigator.hpp>
Public Members
Whether to perform boundary checks for layer resolving (improves navigation for bended tracks)
stop at every material surface (whether it is passive or not)
stop at every surface regardless what it is
Configuration for this Navigator stop at every sensitive surface (whether it has material or not)
Tracking Geometry for this Navigator.
- #include <Acts/Propagator/Navigator.hpp>
Nested State struct.
It acts as an internal state which is created for every propagation/extrapolation step and keep thread-local navigation information
Public Functions
Public Members
Navigation state - external state: the current surface.
Navigation state: the current volume.
Externally provided surfaces - these are tried to be hit.
Force intersection with boundaries.
Indicator that the last VolumeHierarchy surface was reached skip the next layer targeting to the next boundary/volume.
the vector of boundary surfaces to work through
the current boundary index of the navigation state
Navigation state : a break has been detected.
the current layer index of the navigation state
the vector of navigation layers to work through
the current surface index of the navigation state
the vector of navigation surfaces to work through
Navigation state: the start layer.
Indicator for start layer treatment.
Navigation state: the start surface.
Navigation state: the start volume.
Navigation state: the target layer.
Indicator if the target is reached.
Navigation state: the target surface.
Navigation state: the target volume.
Navigation state: the world volume.
-
template<typename external_spacepoint_t>
struct Neighbour - #include <Acts/Seeding/Neighbour.hpp>
A class that helps in processing the neighbours, given a collection of middle space points The idea here is that in the seeding we look for compatible b-m and m-t doublets.
One of the requirements is that the bottom/top space point is at a suitable distance (in radius) w.r.t. the middle space point. We know however that the space points in each bin are sorted in radius. That means we can use this sorting in order to reduce the number of space point to consider when looking for compatible doublets. The idea is to keep track of first space point that is in the allowed bin, by storing its position using an iterator itr This helps us since the lower possible buondary is given by the first middle space point (its radius minus the mad deltaR defined by the user). The subsequent middle space point will have a higher radius. That means that there is no point in looking at neighbour space point before itr, since we know they will be out of range.
Public Functions
-
Neighbour() = delete
default constructor
-
Neighbour(Acts::SpacePointGrid<external_spacepoint_t> &&grid, std::size_t idx, const float lowerBound) = delete
Constructor with grid as rvalue.
- Parameters
grid – The grid containing the space points
idx – The global index of the bin in the grid
lowerBound – The lower bound of the allowed space points
-
Neighbour(const Acts::SpacePointGrid<external_spacepoint_t> &grid, std::size_t idx, const float lowerBound)
Constructor.
- Parameters
grid – The grid containing the space points
idx – The global index of the bin in the grid
lowerBound – The lower bound of the allowed space point
Public Members
-
std::size_t index
The global bin index on the grid.
-
Acts::SpacePointGrid<external_spacepoint_t>::value_type::const_iterator itr
The iterator containing the position of the first space point in the valid radius range.
-
Neighbour() = delete
-
struct Neutral
- #include <Acts/EventData/Charge.hpp>
Charge and momentum interpretation for neutral particles.
Public Functions
-
constexpr Neutral() = default
-
inline constexpr Neutral(float absQ) noexcept
Construct and verify the input charge magnitude (in debug builds).
This constructor is only provided to allow consistent construction.
-
inline constexpr float absQ() const noexcept
-
template<typename T>
inline constexpr auto extractCharge(T) const noexcept
-
template<typename T>
inline constexpr auto extractMomentum(T qOverP) const noexcept
Friends
- inline friend constexpr friend bool operator== (Neutral, Neutral) noexcept
Compare for equality.
This is always
trueasNeutralhas no internal state. Must be available to provide a consistent interface.
-
constexpr Neutral() = default
-
class NeutralParticleHypothesis : public Acts::GenericParticleHypothesis<Neutral>
- #include <Acts/EventData/ParticleHypothesis.hpp>
Specialized particle hypothesis for neutral particles.
Note
This serves as a factory for common neutral particles.
Public Functions
-
template<typename other_charge_t>
inline constexpr NeutralParticleHypothesis(const GenericParticleHypothesis<other_charge_t> &other)
-
inline NeutralParticleHypothesis(PdgParticle absPdg)
-
inline constexpr NeutralParticleHypothesis(PdgParticle absPdg, float mass)
Public Static Functions
-
static inline NeutralParticleHypothesis photon()
-
static inline NeutralParticleHypothesis pion0()
-
template<typename other_charge_t>
-
class NonNeutralCharge
- #include <Acts/EventData/Charge.hpp>
Charge and momentum interpretation for arbitrarily charged but not neutral particles.
Public Functions
-
inline constexpr NonNeutralCharge(float absQ) noexcept
Construct with the magnitude of the input charge.
-
inline constexpr NonNeutralCharge(SinglyCharged) noexcept
-
inline constexpr float absQ() const noexcept
-
template<typename T>
inline constexpr auto extractCharge(T qOverP) const noexcept
-
template<typename T>
inline constexpr auto extractMomentum(T qOverP) const noexcept
Friends
- inline friend constexpr friend bool operator== (NonNeutralCharge lhs, NonNeutralCharge rhs) noexcept
Compare for equality.
-
inline constexpr NonNeutralCharge(float absQ) noexcept
-
class NonNeutralChargedParticleHypothesis : public Acts::GenericParticleHypothesis<NonNeutralCharge>
- #include <Acts/EventData/ParticleHypothesis.hpp>
Specialized particle hypothesis for non-neutral particles.
Note
This serves as a factory for common non-neutral particles.
Public Functions
-
template<typename other_charge_t>
inline constexpr NonNeutralChargedParticleHypothesis(const GenericParticleHypothesis<other_charge_t> &other)
-
inline NonNeutralChargedParticleHypothesis(PdgParticle absPdg)
-
inline constexpr NonNeutralChargedParticleHypothesis(PdgParticle absPdg, float mass, NonNeutralCharge chargeType)
Public Static Functions
-
static inline NonNeutralChargedParticleHypothesis electron()
-
static inline NonNeutralChargedParticleHypothesis muon()
-
static inline NonNeutralChargedParticleHypothesis pion()
-
static inline NonNeutralChargedParticleHypothesis pionLike(float absQ)
-
template<typename other_charge_t>
-
class NullBField : public Acts::MagneticFieldProvider
- #include <Acts/MagneticField/NullBField.hpp>
Null bfield which returns 0 always.
Public Functions
-
NullBField() = default
Default constructor.
-
inline virtual Result<Vector3> getField(const Vector3 &position, MagneticFieldProvider::Cache &cache) const override
Retrieve magnetic field value at a given location.
Requires a cache object created through makeCache().
Note
The
positionis ignored and only kept as argument to provide a consistent interface with other magnetic field services.- Parameters
position – [in] global 3D position for the lookup
cache – [inout] Field provider specific cache object
- Returns
magnetic field vector at given position
-
inline virtual Result<Vector3> getFieldGradient(const Vector3 &position, ActsMatrix<3, 3> &derivative, MagneticFieldProvider::Cache &cache) const override
Retrieve magnetic field value its its gradient.
Requires a cache object created through makeCache().
Note
The
positionis ignored and only kept as argument to provide a consistent interface with other magnetic field services.Note
currently the derivative is not calculated
- Parameters
position – [in] global 3D position
derivative – [out] gradient of magnetic field vector as (3x3) matrix
cache – [inout] Field provider specific cache object
- Returns
magnetic field vector
-
inline bool isInside(const Vector3 &position) const
check whether given 3D position is inside look-up domain
Note
The method will always return true for the null B-Field
- Parameters
position – [in] global 3D position
- Returns
trueif position is inside the defined look-up grid, otherwisefalse
-
inline virtual Acts::MagneticFieldProvider::Cache makeCache(const Acts::MagneticFieldContext &mctx) const override
Make an opaque cache for the magnetic field.
Instructs the specific implementation to generate a
Cacheinstance for magnetic field lookup.- Parameters
mctx – The magnetic field context to generate cache for
- Returns
Cache The opaque cache object
-
struct Cache
- #include <Acts/MagneticField/NullBField.hpp>
Public Functions
-
inline Cache(const MagneticFieldContext&)
constructor with context
-
inline Cache(const MagneticFieldContext&)
-
NullBField() = default
-
template<typename propagator_t, typename propagator_options_t = PropagatorOptions<>>
class NumericalTrackLinearizer - #include <Acts/Vertexing/NumericalTrackLinearizer.hpp>
Linearizes the track parameters at the PCA to a user-provided point (linPoint).
The track parameters are written as a function of the global 4D PCA position and the momentum of the particle at the PCA (i.e., (phi, theta, q/p)). The linearization then reads (see Eq. 5.7 in Ref(1)):
q = A (r - r_0) + B (p - p_0) + c,
where q are the Perigee parameters wrt linPoint, {r_0} r is the {initial} 4D PCA position, {p_0} p is the {initial} momentum at the PCA, and c is the constant term of the expansion. A and B are matrices of derivatives, denoted hereafter as “positionJacobian” and “momentumJacobian” respectively. Note that, unlike in Ref. (1), we add the time to the parametrization, which adds a row and a column to A and a row to B.
This class computes A and B by wiggling one of the 7 parameters at the PCA and computing the new PCA wrt linPoint. The derivatives wrt the k-th parameter pk are then calculated via
(q(p1, p2, …, pk+delta, … p7) - q(p1, p2, …, pk, … p7))/delta,
where q(p1, p2, …, pk+delta, … p7) are the new Perigee parameters (corresponding to the new PCA to linPoint). Note that p1 corresponds to the x-position of the PCA, p2 corresponds to the y-position of the PCA, etc.
Ref.(1) - CERN-THESIS-2010-027, Giacinto Piacquadio (Freiburg U.)
Note
Connection to RiddersPropagator: The RiddersPropagator does a very similar thing to what this class does, but it wiggles BoundTrackParameters (FreeTrackParameters could also be used if Propagator.hpp and Propagator.ipp were adapted to accommodate them). Here, we wiggle neither BoundTrackParameters nor FreeTrackParameters, but rather the parameters described above.
- Template Parameters
propagator_t – Propagator type
propagator_options_t – Propagator options type
Public Types
-
using Propagator_t = propagator_t
Public Functions
-
inline NumericalTrackLinearizer(const Config &config, std::unique_ptr<const Logger> _logger = getDefaultLogger("NumTrkLinProp", Logging::INFO))
Constructor.
- Parameters
config – Configuration object
_logger – Logger instance
-
Result<LinearizedTrack> linearizeTrack(const BoundTrackParameters ¶ms, const Vector4 &linPoint, const Acts::GeometryContext &gctx, const Acts::MagneticFieldContext &mctx, State&) const
Function that linearizes BoundTrackParameters at the PCA to a given Perigee surface.
Note
Transverse plane of the Perigee corresponding to
linPointis parallel to the global x-y plane- Parameters
params – Parameters to linearize
linPoint – Point which defines the Perigee.
gctx – Geometry context
mctx – Magnetic field context
- Returns
Linearized track
-
struct Config
- #include <Acts/Vertexing/NumericalTrackLinearizer.hpp>
Configuration struct.
Public Functions
@ Config constructor if magnetic field is present
- Parameters
bIn – The magnetic field
prop – The propagator
Config constructor without B field -> uses NullBField.
- Parameters
prop – Propagator
Public Members
-
std::shared_ptr<const MagneticFieldProvider> bField
-
ActsScalar delta = 1e-8
Setting size of the perturbation delta for calculation of numerical derivatives (i.e., f’(x) ~ (f(x+delta) - f(x)) / delta)
-
std::shared_ptr<const Propagator_t> propagator
-
ActsScalar targetTolerance = 1e-12
Tolerance determining how close we need to get to a surface to reach it during propagation.
-
struct State
- #include <Acts/Vertexing/NumericalTrackLinearizer.hpp>
State struct.
Public Functions
-
inline State(MagneticFieldProvider::Cache fieldCacheIn)
State constructor.
- Parameters
fieldCacheIn – Magnetic field cache
Public Members
-
MagneticFieldProvider::Cache fieldCache
-
inline State(MagneticFieldProvider::Cache fieldCacheIn)
-
template<typename object_t, typename representation_t = object_t>
class ObjectIntersection - #include <Acts/Utilities/Intersection.hpp>
class extensions to return also the object and a representation
Public Functions
-
ObjectIntersection() = default
Default constructor.
-
template<typename T = representation_t, std::enable_if_t<std::is_same<T, object_t>::value, int> = 0>
inline ObjectIntersection(const Intersection3D &sInter, const object_t *sObject) Object intersection - symmetric setup.
- Parameters
sInter – is the intersection
sObject – is the object to be instersected
-
inline ObjectIntersection(const Intersection3D &sInter, const object_t *sObject, const representation_t *sRepresentation)
Object intersection.
- Parameters
sInter – is the intersection
sObject – is the object to be instersected
sRepresentation – is the object representation
-
inline explicit operator bool() const
Bool() operator for validity checking.
-
inline bool operator<(const ObjectIntersection<object_t, representation_t> &oi) const
Smaller operator for ordering & sorting.
This operator will ignore the alternative, but simply order the representing intersection
- Parameters
oi – is the source intersection for comparison
-
inline bool operator>(const ObjectIntersection<object_t, representation_t> &oi) const
Greater operator for ordering & sorting.
This operator will ignore the alternative, but simply order the representing intersection
- Parameters
oi – is the source intersection for comparison
-
inline void swapSolutions()
Allow swapping the intersection and the alternative.
Public Members
-
Intersection3D alternative = {}
The alternative intersections.
-
Intersection3D intersection = {}
The intersection itself.
-
const object_t *object = {nullptr}
The object that was (tried to be) intersected.
-
const representation_t *representation = {nullptr}
The representation of this object.
-
ObjectIntersection() = default
-
template<class T>
class ObjectSorterT - #include <Acts/Geometry/GeometryObjectSorter.hpp>
Public Functions
-
inline ObjectSorterT(BinningValue bValue)
Constructor from a binning value.
- Parameters
bValue – is the value in which the binning is done
-
inline BinningValue binningValue() const
-
inline ObjectSorterT(BinningValue bValue)
-
template<typename T = double>
class ObjVisualization3D : public Acts::IVisualization3D - #include <Acts/Visualization/ObjVisualization3D.hpp>
This helper produces output in the OBJ format.
Note that colors are not supported in this implementation.
Public Types
-
using LineType = std::pair<size_t, size_t>
Type of a line.
-
using ValueType = T
Stored value type, should be double or float.
-
using VertexType = Eigen::Matrix<ValueType, 3, 1>
Type of a vertex based on the value type.
Public Functions
-
inline ObjVisualization3D(unsigned int prec = 4, double scale = 1.)
Constructor that allows to set scalor and precision.
- Parameters
prec – The output precision with std::setprecision
scale – An (optional) scaling for the writing out
-
virtual void clear() final
Remove all contents of this helper.
-
virtual void face(const std::vector<Vector3> &vtxs, ColorRGB color = {0, 0, 0}) final
Draw a face that connects a list of vertices.
Note
Depending on the helper implementation, out of plane vertices might be handled differently.
- Parameters
vtxs – The vertices that make up the face
color – The color of the face
-
virtual void faces(const std::vector<Vector3> &vtxs, const std::vector<FaceType> &faces, ColorRGB color = {0, 0, 0}) final
Draw a faces that connects a list of vertices - expert only.
Note
Depending on the helper implementation, out of plane vertices might be handled differently.
- Parameters
vtxs – The vertices that make up the faceS
faces – The face presectiotions (i.e. connecting vertices)
color – The color of the face
-
virtual void line(const Vector3 &a, const Vector3 &b, ColorRGB color = {0, 0, 0}) final
Draw a line from a vertex to another.
- Parameters
a – The start vertex
b – The end vertex
color – The color of the line
-
virtual void vertex(const Vector3 &vtx, ColorRGB color = {0, 0, 0}) final
Draw a vertex at a given location and a color.
- Parameters
vtx – The vertex position
color – The color
-
virtual void write(const std::string &path) const final
Write the content of the helper to an outstream.
Note
will change to std::filesystem::path once gcc9 is standard
- Parameters
path – is the file system path for writing the file
-
virtual void write(std::ostream &os) const final
Write the content of the helper to an outstream.
- Parameters
os – The output stream for file
-
void write(std::ostream &os, std::ostream &mos) const
Write the object and the material file.
- Parameters
os – the output stream for the object
mos – the output stream for the auxiliary material file
-
using LineType = std::pair<size_t, size_t>
-
class OnnxEdgeClassifier : public Acts::EdgeClassificationBase
- #include <Acts/Plugins/ExaTrkX/OnnxEdgeClassifier.hpp>
Public Functions
-
~OnnxEdgeClassifier()
-
inline Config config() const
-
virtual std::tuple<std::any, std::any, std::any> operator()(std::any nodes, std::any edges) override
Perform edge classification.
- Parameters
nodes – Node tensor with shape (n_nodes, n_node_features)
edges – Edge-index tensor with shape (2, n_edges)
- Returns
(node_tensor, edge_tensor, score_tensor)
-
struct Config
- #include <Acts/Plugins/ExaTrkX/OnnxEdgeClassifier.hpp>
Public Members
-
float cut = 0.21
-
std::string modelPath
-
float cut = 0.21
-
~OnnxEdgeClassifier()
-
class OnnxMetricLearning : public Acts::GraphConstructionBase
- #include <Acts/Plugins/ExaTrkX/OnnxMetricLearning.hpp>
Public Functions
-
~OnnxMetricLearning()
-
inline Config config() const
-
virtual std::tuple<std::any, std::any> operator()(std::vector<float> &inputValues, std::size_t numNodes) override
Perform the graph construction.
- Parameters
inputValues – Flattened input data
numNodes – number of nodes. inputValues.size() / numNodes then gives the number of features
- Returns
(node_tensor, edge_tensore)
-
struct Config
- #include <Acts/Plugins/ExaTrkX/OnnxMetricLearning.hpp>
Public Members
-
int embeddingDim = 8
-
int knnVal = 500
-
std::string modelPath
-
float rVal = 1.6
-
int spacepointFeatures = 3
-
int embeddingDim = 8
-
~OnnxMetricLearning()
-
class OnnxRuntimeBase
- #include </home/docs/checkouts/readthedocs.org/user_builds/acts/checkouts/v29.0.0/Plugins/Onnx/include/Acts/Plugins/Onnx/OnnxRuntimeBase.hpp>
Subclassed by Acts::MLTrackClassifier
Public Functions
-
OnnxRuntimeBase() = default
Default constructor.
-
OnnxRuntimeBase(Ort::Env &env, const char *modelPath)
Parametrized constructor.
- Parameters
env – the ONNX runtime environment
modelPath – the path to the ML model in *.onnx format
-
~OnnxRuntimeBase() = default
Default destructor.
-
std::vector<std::vector<float>> runONNXInference(NetworkBatchInput &inputTensorValues) const
Run the ONNX inference function for a batch of input.
- Parameters
inputTensorValues – Vector of the input feature values of all the inputs used for prediction
- Returns
The vector of output (predicted) values
-
std::vector<float> runONNXInference(std::vector<float> &inputTensorValues) const
Run the ONNX inference function.
- Parameters
inputTensorValues – The input feature values used for prediction
- Returns
The output (predicted) values
-
std::vector<std::vector<std::vector<float>>> runONNXInferenceMultiOutput(NetworkBatchInput &inputTensorValues) const
Run the multi-output ONNX inference function for a batch of input.
- Parameters
inputTensorValues – Vector of the input feature values of all the inputs used for prediction
- Returns
The vector of output (predicted) values, one for each output
-
OnnxRuntimeBase() = default
-
template<typename, typename H = void>
class OwningDelegate
-
template<typename R, typename H, typename ...Args>
class OwningDelegate<R(Args...), H> : public Acts::Delegate<R(Args...), H, DelegateType::Owning> - #include <Acts/Utilities/Delegate.hpp>
Alias for an owning delegate.
-
struct ParticleData
- #include <Acts/Definitions/ParticleData.hpp>
Public Members
-
float charge = {}
-
float mass = {}
-
std::string_view name
-
float charge = {}
-
class ParticleHypothesis : public Acts::GenericParticleHypothesis<AnyCharge>
- #include <Acts/EventData/ParticleHypothesis.hpp>
Specialized particle hypothesis for any kind of charged particles.
Note
This serves as a factory for common particles with any kind of charge.
Public Functions
-
template<typename other_charge_t>
inline constexpr ParticleHypothesis(const GenericParticleHypothesis<other_charge_t> &other)
-
inline ParticleHypothesis(PdgParticle absPdg)
-
inline constexpr ParticleHypothesis(PdgParticle absPdg, float mass, AnyCharge chargeType)
Public Static Functions
-
static inline ParticleHypothesis electron()
-
static inline ParticleHypothesis muon()
-
static inline ParticleHypothesis photon()
-
static inline ParticleHypothesis pion()
-
static inline ParticleHypothesis pion0()
-
static inline ParticleHypothesis pionLike(float absQ)
-
template<typename other_charge_t>
-
class PassiveLayerBuilder : public Acts::ILayerBuilder
- #include <Acts/Geometry/PassiveLayerBuilder.hpp>
The PassiveLayerBuilder is able to build cylinder & disc layers with given dimensions and material.
The specifications of the layers have to be given by the configuration struct.
Public Functions
-
PassiveLayerBuilder(const Config &plConfig, std::unique_ptr<const Logger> logger = getDefaultLogger("PassiveLayerBuilder", Logging::INFO))
Constructor.
- Parameters
plConfig – is the ocnfiguration struct that steers behavior
logger – logging instance
-
~PassiveLayerBuilder() override = default
Destructor.
-
virtual const LayerVector centralLayers(const GeometryContext &gctx) const override
LayerBuilder interface method.
- Parameters
gctx – is the geometry context under which the geometry is built
- Returns
the layers at the central sector
-
inline Config getConfiguration() const
Get configuration method.
-
inline virtual const std::string &identification() const override
Name identification.
- Returns
the string based identification
-
virtual const LayerVector negativeLayers(const GeometryContext &gctx) const override
LayerBuilder interface method.
- Parameters
gctx – is the geometry context under which the geometry is built
- Returns
the layers at negative side
-
virtual const LayerVector positiveLayers(const GeometryContext &gctx) const override
LayerBuilder interface method.
- Parameters
gctx – is the geometry context under which the geometry is built
- Returns
the layers at positive side
-
void setConfiguration(const Config &plConfig)
Set configuration method.
- Parameters
plConfig – is a configuration struct it overwrites the current configuration
-
void setLogger(std::unique_ptr<const Logger> newLogger)
Set logging instance.
- Parameters
newLogger – the logger instance
-
struct Config
- #include <Acts/Geometry/PassiveLayerBuilder.hpp>
Configuration struct for the passive layer builder This nested struct is used to configure the layer building.
Public Members
-
std::vector<double> centralLayerHalflengthZ
central layer specs
-
std::vector<std::shared_ptr<const ISurfaceMaterial>> centralLayerMaterial
central layer specs
-
std::vector<double> centralLayerRadii
central layer specs
-
std::vector<double> centralLayerThickness
central layer specs
-
std::string layerIdentification
string based identification
-
std::vector<std::shared_ptr<const ISurfaceMaterial>> posnegLayerMaterial
p/n layer specs
-
std::vector<double> posnegLayerPositionZ
p/n layer specs
-
std::vector<double> posnegLayerRmax
p/n layer specs
-
std::vector<double> posnegLayerRmin
p/n layer specs
-
std::vector<double> posnegLayerThickness
p/n layer specs
-
std::vector<double> centralLayerHalflengthZ
-
PassiveLayerBuilder(const Config &plConfig, std::unique_ptr<const Logger> logger = getDefaultLogger("PassiveLayerBuilder", Logging::INFO))
-
struct PathLimitReached
- #include <Acts/Propagator/StandardAborters.hpp>
This is the condition that the pathLimit has been reached.
Public Functions
boolean operator for abort condition without using the result
- Template Parameters
propagator_state_t – Type of the propagator state
stepper_t – Type of the stepper
navigator_t – Type of the navigator
- Parameters
state – [inout] The propagation state object
stepper – [in] Stepper used for propagation
navigator – [in] Navigator used for propagation
logger – a logger instance
Public Members
-
double internalLimit = std::numeric_limits<double>::max()
Boolean switch for Loop protection.
-
class PerigeeSurface : public Acts::LineSurface
- #include <Acts/Surfaces/PerigeeSurface.hpp>
Class describing the Line to which the Perigee refers to.
The Surface axis is fixed to be the z-axis of the Tracking frame. It inherits from StraingLineSurface.

Public Functions
-
PerigeeSurface() = delete
Default Constructor - deleted.
-
~PerigeeSurface() override = default
Destructor - defaulted.
-
virtual std::string name() const final
Return properly formatted class name for screen output */.
-
PerigeeSurface &operator=(const PerigeeSurface &other)
Assignment operator.
- Parameters
other – is the source surface to be assigned
-
virtual Polyhedron polyhedronRepresentation(const GeometryContext &gctx, size_t lseg) const final
Return a Polyhedron for the surfaces.
Note
ignored
- Parameters
gctx – The current geometry context object, e.g. alignment
lseg – is ignored for a perigee
- Returns
A list of vertices and a face/facett description of it
-
virtual std::ostream &toStream(const GeometryContext &gctx, std::ostream &sl) const final
Output Method for std::ostream.
- Parameters
gctx – The current geometry context object, e.g. alignment
sl – is the ostream to be dumped into
- Returns
ostreamn object which was streamed into
-
virtual SurfaceType type() const final
Return the surface type.
-
PerigeeSurface() = delete
-
class PlanarBounds : public Acts::SurfaceBounds
- #include <Acts/Surfaces/PlanarBounds.hpp>
common base class for all bounds that are in a local x/y cartesian frame
simply introduced to avoid wrong bound assignments to surfaces
Subclassed by Acts::ConvexPolygonBoundsBase, Acts::DiamondBounds, Acts::EllipseBounds, Acts::RectangleBounds, Acts::TrapezoidBounds
Public Functions
-
virtual const RectangleBounds &boundingBox() const = 0
Bounding box parameters.
- Returns
rectangle bounds for a bounding box
-
virtual std::vector<Vector2> vertices(unsigned int lseg = 1) const = 0
Return the vertices.
Note
that the extremas are given, which may slightly alter the number of segments returned
- Parameters
lseg – the number of segments used to approximate and eventually curved line
- Returns
vector for vertices in 2D
-
class PlanarModuleCluster : public Acts::Measurement<BoundIndices, 3>
- #include <Acts/Digitization/PlanarModuleCluster.hpp>
Public Functions
Constructor from DigitizationCells.
- Parameters
surface – [in] The surface the cluster is on
sourceLink – [in] is the link to the truth information
cov – [in] is the covariance matrix
loc0 – [in] is the local position in the first coordinate
loc1 – [in] is the local position in the second coordinate
t – [in] Timestamp of the cluster
dCells – [in] is the vector of digitization cells
dModule – [in] an optional pointer to a digitization configuration
-
inline const std::vector<DigitizationCell> &digitizationCells() const
access to the digitization cells
- Returns
the vector to the digitization cells
-
inline const DigitizationModule *digitizationModule() const
access to the digitization module
- Returns
the pointer to the digitization module
-
inline const Surface &referenceObject() const
Module surface.
-
class PlanarModuleStepper
- #include <Acts/Digitization/PlanarModuleStepper.hpp>
Module for fast, geometric digitization this is a planar module stepper that calculates the step length in given segmentations and retrunes digitisation steps.
Public Functions
-
PlanarModuleStepper(std::unique_ptr<const Logger> mlogger = getDefaultLogger("PlanarModuleStepper", Logging::INFO))
Constructor.
- Parameters
mlogger – is the logging instance
-
~PlanarModuleStepper() = default
Destructor.
-
std::vector<DigitizationStep> cellSteps(const GeometryContext &gctx, const DigitizationModule &dmodule, const Vector2 &moduleIntersection, const Vector3 &trackDirection) const
Calculate the steps caused by this track - fast simulation interface.
- Parameters
gctx – The current geometry context object, e.g. alignment
dmodule – is the digitization module
moduleIntersection – is the 2d intersection at the module surface
trackDirection – is the track direction at the intersection
- Returns
is the vector of digitization steps
-
std::vector<DigitizationStep> cellSteps(const GeometryContext &gctx, const DigitizationModule &dmodule, const Vector3 &startPoint, const Vector3 &endPoint) const
Calculate the steps caused by this track - full simulation interface.
- Parameters
gctx – The current geometry context object, e.g. alignment
dmodule – is the digitization module
startPoint – is the starting position of the stepping
endPoint – is the end position of the stepping
- Returns
is the vector of digitization steps
-
inline void setLogger(std::unique_ptr<const Logger> logger)
Set logging instance.
- Parameters
logger – is the logging instance to be set
-
PlanarModuleStepper(std::unique_ptr<const Logger> mlogger = getDefaultLogger("PlanarModuleStepper", Logging::INFO))
-
class PlaneLayer : public virtual Acts::PlaneSurface, public Acts::Layer
- #include <Acts/Geometry/PlaneLayer.hpp>
Class to describe a planar detector layer for tracking, it inhertis from both, Layer base class and PlaneSurface class.
Public Functions
-
PlaneLayer() = delete
-
PlaneLayer(const PlaneLayer &pla) = delete
-
~PlaneLayer() override = default
-
PlaneLayer &operator=(const PlaneLayer&) = delete
-
virtual const PlaneSurface &surfaceRepresentation() const override
Transforms the layer into a Surface representation for extrapolation.
- Returns
returns a reference to a PlaneSurface
-
virtual PlaneSurface &surfaceRepresentation() override
Public Static Functions
Factory for a shared plane layer.
- Parameters
transform – which places the layer in the global frame
pbounds – the planar bounds that define the layer dimensions
surfaceArray – is the surface array that holds the sensitive surfaces
thickness – is the thickness of the layer (normal direction to plane)
ad – is the approach descriptor for describing the approach surface
laytyp – is the layer type
- Returns
shared pointer to a PlaneLayer
-
PlaneLayer() = delete
-
class PlaneSurface : public Acts::Surface
- #include <Acts/Surfaces/PlaneSurface.hpp>
Class for a planaer in the TrackingGeometry.
The PlaneSurface extends the Surface class with the possibility to convert local to global positions (vice versa).
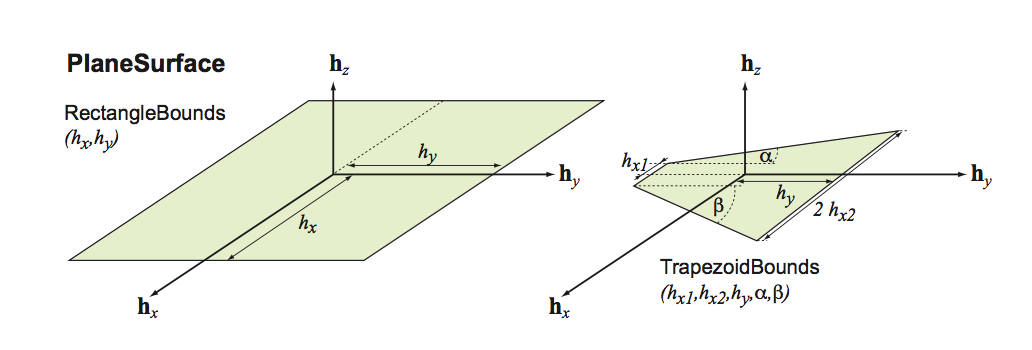
Subclassed by Acts::PlaneLayer
Public Functions
-
PlaneSurface() = delete
-
~PlaneSurface() override = default
-
virtual Vector3 binningPosition(const GeometryContext &gctx, BinningValue bValue) const final
The binning position is the position calculated for a certain binning type.
- Parameters
gctx – The current geometry context object, e.g. alignment
bValue – is the binning type to be used
- Returns
position that can beused for this binning
-
virtual const SurfaceBounds &bounds() const override
Return method for bounds object of this surfrace.
-
virtual Result<Vector2> globalToLocal(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, double tolerance = s_onSurfaceTolerance) const override
Global to local transformation.
Note
For planar surfaces the momentum direction is ignored in the global to local transformation
- Parameters
gctx – The current geometry context object, e.g. alignment
position – global 3D position - considered to be on surface but not inside bounds (check is done)
direction – global 3D momentum direction (optionally ignored) method symmetry)
tolerance – optional tolerance within which a point is considered valid on surface
- Returns
a Result<Vector2> which can be !ok() if the operation fails
-
virtual SurfaceIntersection intersect(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck = false, ActsScalar tolerance = s_onSurfaceTolerance) const final
Straight line intersection.
mathematical motivation:
the equation of the plane is given by: \( \vec n \cdot \vec x = \vec n \cdot \vec p,\) where \( \vec n = (n_{x}, n_{y}, n_{z})\) denotes the normal vector of the plane, \( \vec p = (p_{x}, p_{y}, p_{z})\) one specific point on the plane and \( \vec x = (x,y,z) \) all possible points on the plane.
Given a line with:\( \vec l(u) = \vec l_{1} + u \cdot \vec v \)
,
the solution for
\( u \) can be written: \( u = \frac{\vec n (\vec p - \vec l_{1})}{\vec n \vec v}\) If the denominator is 0 then the line lies:either in the plane
perpendicular to the normal of the plane
Note
expected to be normalized)
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The start position of the intersection attempt
direction – The direction of the intersection attempt, (
bcheck – The boundary check directive
tolerance – the tolerance used for the intersection
- Returns
the SurfaceIntersection object
-
virtual ActsMatrix<2, 3> localCartesianToBoundLocalDerivative(const GeometryContext &gctx, const Vector3 &position) const final
Calculate the derivative of bound track parameters local position w.r.t.
position in local 3D Cartesian coordinates
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The position of the parameters in global
- Returns
Derivative of bound local position w.r.t. position in local 3D cartesian coordinates
-
virtual Vector3 localToGlobal(const GeometryContext &gctx, const Vector2 &lposition, const Vector3 &direction) const override
Local to global transformation.
Note
For planar surfaces the momentum direction is ignored in the local to global transformation
- Parameters
gctx – The current geometry context object, e.g. alignment
lposition – local 2D position in specialized surface frame
direction – global 3D momentum direction (optionally ignored)
- Returns
the global position by value
-
virtual std::string name() const override
Return properly formatted class name for screen output.
-
inline Vector3 normal(const GeometryContext &gctx) const
Normal vector return without argument.
-
virtual Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const final
Normal vector return.
return a Vector3 by value
- Parameters
gctx – The current geometry context object, e.g. alignment
lposition – is the local position is ignored
-
Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const = 0
Normal vector return without argument.
-
Vector3 normal(const GeometryContext &gctx, const Vector3 &position) const
Normal vector return without argument.
-
PlaneSurface &operator=(const PlaneSurface &other)
Assignment operator.
- Parameters
other – The source PlaneSurface for assignment
-
virtual double pathCorrection(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const final
Method that calculates the correction due to incident angle.
Note
this is the final implementation of the pathCorrection function
- Parameters
gctx – The current geometry context object, e.g. alignment
position – global 3D position - considered to be on surface but not inside bounds (check is done)
direction – global 3D momentum direction (ignored for PlaneSurface)
- Returns
a double representing the scaling factor
-
virtual Polyhedron polyhedronRepresentation(const GeometryContext &gctx, size_t lseg) const override
Return a Polyhedron for the surfaces.
- Parameters
gctx – The current geometry context object, e.g. alignment
lseg – Number of segments along curved lines, it represents the full 2*M_PI coverange, if lseg is set to 1 only the extrema are given
- Returns
A list of vertices and a face/facett description of it
-
virtual SurfaceType type() const override
Return the surface type.
-
PlaneSurface() = delete
-
template<typename T = double>
class PlyVisualization3D : public Acts::IVisualization3D - #include <Acts/Visualization/PlyVisualization3D.hpp>
Helper to write out PlyVisualization3D visualization format.
Public Types
-
using ValueType = T
Stored value type, should be double or float.
-
using VertexType = Eigen::Matrix<ValueType, 3, 1>
Type of a vertex based on the value type.
Public Functions
-
virtual void clear() final
Remove all contents of this helper.
-
virtual void face(const std::vector<Vector3> &vtxs, ColorRGB color = {120, 120, 120}) final
Draw a face that connects a list of vertices.
Note
Depending on the helper implementation, out of plane vertices might be handled differently.
- Parameters
vtxs – The vertices that make up the face
color – The color of the face
-
virtual void faces(const std::vector<Vector3> &vtxs, const std::vector<FaceType> &faces, ColorRGB color = {120, 120, 120}) final
Draw a faces that connects a list of vertices - expert only.
Note
Depending on the helper implementation, out of plane vertices might be handled differently.
- Parameters
vtxs – The vertices that make up the faceS
faces – The face presectiotions (i.e. connecting vertices)
color – The color of the face
-
virtual void line(const Vector3 &a, const Vector3 &b, ColorRGB color = {120, 120, 120}) final
Draw a line from a vertex to another.
- Parameters
a – The start vertex
b – The end vertex
color – The color of the line
-
virtual void vertex(const Vector3 &vtx, ColorRGB color = {120, 120, 120}) final
Draw a vertex at a given location and a color.
- Parameters
vtx – The vertex position
color – The color
-
virtual void write(const std::string &path) const final
Write the content of the helper to an outstream.
Note
will change to std::filesystem::path once gcc9 is standard
- Parameters
path – is the file system path for writing the file
-
virtual void write(std::ostream &os) const final
Write the content of the helper to an outstream.
- Parameters
os – The output stream for file
-
using ValueType = T
-
class Polyhedron
- #include <Acts/Geometry/Polyhedron.hpp>
Struct which contains a cartesian approximation for any surface type.
It contains a list of cartesian vertices in the global frame, and additionally a list of lists of indices which indicate which vertices form a face. Each entry in
facesis a face, which is in turn a list of vertices that need to be connected to form a face. This allows theobjStringmethod to produce a ready-to-go obj output.Public Types
-
using FaceType = std::vector<size_t>
Public Functions
-
Polyhedron() = default
Default constructor.
-
inline Polyhedron(const std::vector<Vector3> &verticesIn, const std::vector<FaceType> &facesIn, const std::vector<FaceType> &triangularMeshIn, bool isExact = true)
Default constructor from a vector of vertices and a vector of faces.
Note
This creates copies of the input vectors
- Parameters
verticesIn – The 3D global vertices that make up the object
facesIn – List of lists of indices for faces.
triangularMeshIn – List of lists of indices for a triangular mesh
isExact – A dedicated flag if this is exact or not
-
Extent extent(const Transform3 &transform = Transform3::Identity()) const
Maximum extent of the polyhedron in space.
- Parameters
transform – An (optional) transform to apply to the vertices for estimation the extent with respect to a given coordinate frame
- Returns
ranges that describe the space taken by this surface
-
void merge(const Polyhedron &other)
Merge another Polyhedron into this one.
- Parameters
other – is the source representation
-
void move(const Transform3 &transform)
Move the polyhedron with a Transfrom3D.
- Parameters
transform – The additional transform applied
Public Members
-
bool exact = true
Is this an exact representation (approximating curved spaces)
-
std::vector<FaceType> faces
List of faces connecting the vertices.
each face is a list of vertices v corresponding to the vertex vector above
-
std::vector<FaceType> triangularMesh
List of faces connecting the vertices.
each face is a list of vertices v
in this case restricted to a triangular representation
-
std::vector<Vector3> vertices
List of 3D vertices as vectors.
-
using FaceType = std::vector<size_t>
-
template<typename stepper_t, typename navigator_t = detail::VoidNavigator>
class Propagator - #include <Acts/Propagator/Propagator.hpp>
Propagator for particles (optionally in a magnetic field)
The Propagator works with a state objects given at function call This state object contains the thread local state objects
Navigator::state_type for object navigation and screen output
Stepper::state_type state for the actual transport caching (pos,dir,field)
This Propagator class serves as high-level steering code for propagating track parameters. The actual implementation of the propagation has to be implemented in the stepper_t object, which has to provide the following:
a function for performing a single propagation step
a type mapping for: initial track parameter type -> type of final track parameters
a type mapping for: (initial track parameter type and destination surface type) -> type of final track parameters
a type mapping for: initial track parameter type -> type of internal state object
a type mapping for: (initial track parameter type and destination surface type) -> type of internal state object
- Template Parameters
stepper_t – Type of stepper implementation of the propagation
naviagor_t – Type of the navigator (optional)
Public Types
-
template<typename parameters_t, typename action_list_t>
using action_list_t_result_t = typename result_type_helper<parameters_t, action_list_t>::type Short-hand type definition for propagation result derived from an action list.
- Template Parameters
parameters_t – Type of the final track parameters
action_list_t – List of propagation action types
Type of the navigator in use for public scope.
Typedef the navigator state.
-
using Stepper = stepper_t
Type of the stepper in use for public scope.
-
using StepperState = typename Stepper::State
Type of state object used by the propagation implementation.
Public Functions
Constructor from implementation object.
- Parameters
stepper – The stepper implementation is moved to a private member
navigator – The navigator implementation, moved to a private member
_logger – a logger instance
-
template<typename parameters_t, typename propagator_options_t, typename path_aborter_t = PathLimitReached>
Result<action_list_t_result_t<CurvilinearTrackParameters, typename propagator_options_t::action_list_type>> propagate(const parameters_t &start, const propagator_options_t &options) const Propagate track parameters.
This function performs the propagation of the track parameters using the internal stepper implementation, until at least one abort condition is fulfilled or the maximum number of steps/path length provided in the propagation options is reached.
- Template Parameters
parameters_t – Type of initial track parameters to propagate
propagator_options_t – Type of the propagator options
path_aborter_t – The path aborter type to be added
- Parameters
start – [in] initial track parameters to propagate
options – [in] Propagation options, type Options<,>
- Returns
Propagation result containing the propagation status, final track parameters, and output of actions (if they produce any)
-
template<typename parameters_t, typename propagator_options_t, typename path_aborter_t = PathLimitReached>
Result<action_list_t_result_t<CurvilinearTrackParameters, typename propagator_options_t::action_list_type>> propagate(const parameters_t &start, const propagator_options_t &options, action_list_t_result_t<CurvilinearTrackParameters, typename propagator_options_t::action_list_type> &&inputResult) const Propagate track parameters.
This function performs the propagation of the track parameters using the internal stepper implementation, until at least one abort condition is fulfilled or the maximum number of steps/path length provided in the propagation options is reached.
- Template Parameters
parameters_t – Type of initial track parameters to propagate
propagator_options_t – Type of the propagator options
path_aborter_t – The path aborter type to be added
- Parameters
start – [in] initial track parameters to propagate
options – [in] Propagation options, type Options<,>
inputResult – [in] an existing result object to start from
- Returns
Propagation result containing the propagation status, final track parameters, and output of actions (if they produce any)
-
template<typename parameters_t, typename propagator_options_t, typename target_aborter_t = SurfaceReached, typename path_aborter_t = PathLimitReached>
Result<action_list_t_result_t<BoundTrackParameters, typename propagator_options_t::action_list_type>> propagate(const parameters_t &start, const Surface &target, const propagator_options_t &options) const Propagate track parameters - User method.
This function performs the propagation of the track parameters according to the internal implementation object until at least one abort condition is fulfilled, the destination surface is hit or the maximum number of steps/path length as given in the propagation options is reached.
- Template Parameters
parameters_t – Type of initial track parameters to propagate
propagator_options_t – Type of the propagator options
target_aborter_t – The target aborter type to be added
path_aborter_t – The path aborter type to be added
- Parameters
start – [in] Initial track parameters to propagate
target – [in] Target surface of to propagate to
options – [in] Propagation options
- Returns
Propagation result containing the propagation status, final track parameters, and output of actions (if they produce any)
-
template<typename parameters_t, typename propagator_options_t, typename target_aborter_t = SurfaceReached, typename path_aborter_t = PathLimitReached>
Result<action_list_t_result_t<BoundTrackParameters, typename propagator_options_t::action_list_type>> propagate(const parameters_t &start, const Surface &target, const propagator_options_t &options, action_list_t_result_t<BoundTrackParameters, typename propagator_options_t::action_list_type> inputResult) const Propagate track parameters - User method.
This function performs the propagation of the track parameters according to the internal implementation object until at least one abort condition is fulfilled, the destination surface is hit or the maximum number of steps/path length as given in the propagation options is reached.
- Template Parameters
parameters_t – Type of initial track parameters to propagate
propagator_options_t – Type of the propagator options
target_aborter_t – The target aborter type to be added
path_aborter_t – The path aborter type to be added
- Parameters
start – [in] Initial track parameters to propagate
target – [in] Target surface of to propagate to
options – [in] Propagation options
inputResult – [in] an existing result object to start from
- Returns
Propagation result containing the propagation status, final track parameters, and output of actions (if they produce any)
-
template<typename propagator_options_t>
struct State - #include <Acts/Propagator/Propagator.hpp>
private Propagator state for navigation and debugging
This struct holds the common state information for propagating which is independent of the actual stepper implementation.
- Template Parameters
parameters_t – Type of the track parameters
propagator_options_t – Type of the Objections object
Public Functions
Create the propagator state from the options.
- Template Parameters
propagator_options_t – the type of the propagator options
- Parameters
topts – The options handed over by the propagate call
steppingIn – Stepper state instance to begin with
navigationIn – Navigator state instance to begin with
Public Members
-
std::reference_wrapper<const GeometryContext> geoContext
Context object for the geometry.
Navigation state - internal state of the Navigator.
-
propagator_options_t options
These are the options - provided for each propagation step.
-
StepperState stepping
Stepper state - internal state of the Stepper.
-
template<typename action_list_t = ActionList<>, typename aborter_list_t = AbortList<>>
struct PropagatorOptions : public Acts::PropagatorPlainOptions - #include <Acts/Propagator/Propagator.hpp>
Options for propagate() call.
- Template Parameters
action_list_t – List of action types called after each propagation step with the current propagation and stepper state
aborter_list_t – List of abort conditions tested after each propagation step using the current propagation and stepper state
Public Functions
-
PropagatorOptions() = delete
Delete default constructor.
-
inline PropagatorOptions(const GeometryContext &gctx, const MagneticFieldContext &mctx)
PropagatorOptions with context.
-
PropagatorOptions(const PropagatorOptions<action_list_t, aborter_list_t> &po) = default
PropagatorOptions copy constructor.
-
template<typename extended_aborter_list_t>
inline PropagatorOptions<action_list_t, extended_aborter_list_t> extend(extended_aborter_list_t aborters) const Expand the Options with extended aborters.
- Template Parameters
extended_aborter_list_t – Type of the new aborter list
- Parameters
aborters – The new aborter list to be used (internally)
-
inline void setPlainOptions(const PropagatorPlainOptions &pOptions)
Set the plain options.
- Parameters
pOptions – The plain options
Public Members
-
aborter_list_t abortList
List of abort conditions.
-
action_list_t actionList
List of actions.
-
std::reference_wrapper<const GeometryContext> geoContext
The context object for the geometry.
-
std::reference_wrapper<const MagneticFieldContext> magFieldContext
The context object for the magnetic field.
-
struct PropagatorPlainOptions
- #include <Acts/Propagator/Propagator.hpp>
Class holding the trivial options in propagator options.
Subclassed by Acts::PropagatorOptions< ActionList<>, AbortList<> >, Acts::PropagatorOptions< action_list_t, aborter_list_t >
Public Members
-
PdgParticle absPdgCode = PdgParticle::ePionPlus
The |pdg| code for (eventual) material integration - pion default.
-
double loopFraction = 0.5
Allowed loop fraction, 1 is a full loop.
-
bool loopProtection = true
Loop protection step, it adapts the pathLimit.
-
double mass = 139.57018 * UnitConstants::MeV
The mass of the particle for (eventual) material integration - pion default.
-
unsigned int maxRungeKuttaStepTrials = 10000
Maximum number of Runge-Kutta steps for the stepper step call.
-
unsigned int maxSteps = 1000
Maximum number of steps for one propagate call.
-
double maxStepSize = std::numeric_limits<double>::max()
Absolute maximum step size.
-
double pathLimit = std::numeric_limits<double>::max()
Absolute maximum path length.
-
double stepSizeCutOff = 0.
Cut-off value for the step size.
-
double targetTolerance = s_onSurfaceTolerance
Required tolerance to reach target (surface, pathlength)
-
double tolerance = 1e-4
Tolerance for the error of the integration.
-
PdgParticle absPdgCode = PdgParticle::ePionPlus
-
template<typename parameters_t, typename ...result_list>
struct PropagatorResult : private detail::Extendable<result_list...> - #include <Acts/Propagator/Propagator.hpp>
Simple class holding result of propagation call.
- Template Parameters
parameters_t – Type of final track parameters
result_list – Result pack for additional propagation quantities
Public Members
-
std::optional<parameters_t> endParameters = std::nullopt
Final track parameters.
-
double pathLength = 0.
Signed distance over which the parameters were propagated.
-
unsigned int steps = 0
Number of propagation steps that were carried out.
-
std::optional<BoundMatrix> transportJacobian = std::nullopt
Full transport jacobian.
-
struct ProtoDetector
- #include <Acts/Detector/ProtoDetector.hpp>
A proto detector description being used to define an overall structure of either a TrackingGeometry or Experimental::Detector.
Public Functions
-
inline void harmonize(bool legacy = true)
Harmonize the detector information, this can run in two modes, steered by the.
The legacy mode prepares everything for
Acts::TrackingVolume, if off it creates a description forActs::Detector.- Parameters
legacy – boolean
-
std::string toString(const std::string &indent = "") const
Write the tracking volume to screen.
- Parameters
indent – the current indentation
-
inline void harmonize(bool legacy = true)
-
struct ProtoLayer
- #include <Acts/Geometry/ProtoLayer.hpp>
Encapsulates min/max boundaries that will be turned into a layer.
The struct allows this information to be obtained in a consistent way, or be caller provided.
Public Functions
-
ProtoLayer() = default
-
ProtoLayer(const GeometryContext &gctx, const std::vector<const Surface*> &surfaces)
Constructor.
Loops over a provided vector of surface and calculates the various min/max values in one go. Also takes into account the thickness of an associated DetectorElement, if it exists.
- Parameters
gctx – The current geometry context object, e.g. alignment
surfaces – The vector of surfaces to consider
Constructor.
Loops over a provided vector of surface and calculates the various min/max values in one go. Also takes into account the thickness of an associated DetectorElement, if it exists.
- Parameters
gctx – The current geometry context object, e.g. alignment
surfaces – The vector of surfaces to consider
-
void add(const GeometryContext &gctx, const Surface &surface)
Add a surface, this will also increase the extent.
- Parameters
gctx – The current geometry context object, e.g. alignment
surface – The surface which is added to the ProtoLayer
-
double max(BinningValue bval, bool addenv = true) const
- Parameters
bval – The accessed binning value
addenv – The steering if enevlope is added or not
-
double medium(BinningValue bval, bool addenv = true) const
- Parameters
bval – The accessed binning value
addenv – The steering if enevlope is added or not
-
double min(BinningValue bval, bool addenv = true) const
Get the parameters : min.
- Parameters
bval – The accessed binning value
addenv – The steering if enevlope is added or not
-
double range(BinningValue bval, bool addenv = true) const
- Parameters
bval – The accessed binning value
addenv – The steering if enevlope is added or not
-
inline const std::vector<const Surface*> &surfaces() const
Give access to the surfaces used/assigned to the ProtoLayer.
-
std::ostream &toStream(std::ostream &sl) const
Output to ostream.
- Parameters
sl – the input ostream
Public Members
-
ExtentEnvelope envelope = zeroEnvelopes
The envelope parameters.
-
Extent extent
The extent of the ProtoLayer.
-
ProtoLayer() = default
-
class ProtoLayerHelper
- #include <Acts/Geometry/ProtoLayerHelper.hpp>
This class is designed to parse a vector of Surfaces and sort them into corresponding proto layers.
Public Types
-
using SortingConfig = std::pair<BinningValue, double>
Public Functions
-
inline ProtoLayerHelper(const Config &config, std::unique_ptr<const Logger> logger = getDefaultLogger("ProtoLayerHelper", Logging::INFO))
Constructor with explicit config.
- Parameters
config – Explicit config struct
logger – logging instance
-
~ProtoLayerHelper() = default
-
std::vector<ProtoLayer> protoLayers(const GeometryContext &gctx, const std::vector<const Surface*> &surfaces, const SortingConfig &sorting) const
Sort the surfaces into ProtoLayers.
- Parameters
gctx – The geometry context (usually building context at this stage)
surfaces – The surfaces to be sorted into arrays
sorting – The sorting setup, one single sorting
- Returns
A vector of ProtoLayers
-
std::vector<ProtoLayer> protoLayers(const GeometryContext &gctx, const std::vector<const Surface*> &surfaces, const std::vector<SortingConfig> &sortings) const
Sort the surfaces into ProtoLayers, sequential sorting.
- Parameters
gctx – The geometry context (usually building context at this stage)
surfaces – The surfaces to be sorted into arrays
sortings – The sequential sorting setup
- Returns
A vector of ProtoLayers
-
struct Config
- #include <Acts/Geometry/ProtoLayerHelper.hpp>
-
using SortingConfig = std::pair<BinningValue, double>
-
class ProtoSurfaceMaterial : public Acts::ISurfaceMaterial
- #include <Acts/Material/ProtoSurfaceMaterial.hpp>
proxy to SurfaceMaterial hand over BinUtility
The ProtoSurfaceMaterial class acts as a proxy to the SurfaceMaterial to mark the layers and surfaces on which the material should be mapped on at construction time of the geometry and to hand over the granularity of of the material map with the bin Utility.
Public Functions
-
ProtoSurfaceMaterial() = default
Constructor without BinUtility - homogeneous material.
-
ProtoSurfaceMaterial(const BinUtility &binUtility, MappingType mappingType = MappingType::Default)
Constructor with BinUtility - multidimensional material.
- Parameters
binUtility – a BinUtility determining the granularity and binning of the material on the surface/layer
mappingType – is the type of surface mapping associated to the surface
-
ProtoSurfaceMaterial(const ProtoSurfaceMaterial &smproxy) = default
Copy constructor.
- Parameters
smproxy – The source proxy
-
ProtoSurfaceMaterial(ProtoSurfaceMaterial &&smproxy) = default
Copy move constructor.
- Parameters
smproxy – The source proxy
-
~ProtoSurfaceMaterial() override = default
Destructor.
-
inline const BinUtility &binUtility() const
Return the BinUtility.
-
inline virtual const MaterialSlab &materialSlab(const Vector2 &lp) const final
Return method for full material description of the Surface - from local coordinates.
- Parameters
lp – is local positioning vector
- Returns
will return dummy material
-
inline virtual const MaterialSlab &materialSlab(const Vector3 &gp) const final
Return method for full material description of the Surface - from the global coordinates.
- Parameters
gp – is the global positioning vector
- Returns
will return dummy material
-
inline virtual const MaterialSlab &materialSlab(size_t ib0, size_t ib1) const final
Direct access via bins to the MaterialSlab.
- Parameters
ib0 – indicates the first bin
ib1 – indicates the second bin
- Returns
will return dummy material
-
virtual ProtoSurfaceMaterial &operator*=(double scale) final
Scale operator.
- Parameters
scale – The value to scale this material by
-
ProtoSurfaceMaterial &operator=(const ProtoSurfaceMaterial &smproxy) = default
Assignment operator.
- Parameters
smproxy – The source proxy
-
ProtoSurfaceMaterial &operator=(ProtoSurfaceMaterial &&smproxy) = default
Assignment move operator.
- Parameters
smproxy – The source proxy
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream, to be overloaded by child classes.
-
ProtoSurfaceMaterial() = default
-
struct ProtoVolume
- #include <Acts/Detector/ProtoDetector.hpp>
A proto volume description being used to define an overall structure of either a TrackingVolume or Experimental::DetectorVolume.
Public Functions
-
void constrainDown(const ProtoVolume &ptVolume)
Constrain the daughter volumes with this volume.
- Parameters
ptVolume – is the proto volume from which the constrain is taken
-
void extendUp(ProtoVolume &ptVolume)
Extend the tracking volume with its own constituents, upwards here means that extents are promoted to the mother.
- Parameters
ptVolume – the protoVolume
-
void harmonize(bool legacy = true)
Harmonize the detector information, this can run in two modes, steered by the.
The legacy mode prepares everything for
Acts::TrackingVolume, if off it creates a description forActs::Detector.- Parameters
legacy – boolean
-
bool operator==(const ProtoVolume &ptVolume) const
Define an operator==.
- Parameters
ptVolume – the proto volume to be checked
-
void propagateMaxDown(BinningValue bValue)
Extend the tracking volume with its own constituents.
- Parameters
bValue – the binning value that is propagated
-
void propagateMinDown(BinningValue bValue)
Extend the tracking volume with its own constituents.
- Parameters
bValue – the binning value that is propagated
-
std::string toString(const std::string &indent = "") const
Write the tracking volume to screen.
- Parameters
indent – the current indentation
Public Members
-
Experimental::DetectorBlockBuilder blockBuilder
An attached Detector volume Builder - new detector schema.
-
std::optional<ContainerStructure> container = std::nullopt
Information about container structure - legacy building.
-
Extent extent
The extent of this volume.
-
std::optional<InternalStructure> internal = std::nullopt
Information about internal structure - legacy building.
-
std::string name = ""
Name of the proto volume.
-
struct ContainerStructure
- #include <Acts/Detector/ProtoDetector.hpp>
Public Members
-
std::vector<BinningData> constituentBinning = {}
The constituent binning if this a container.
-
std::vector<ProtoVolume> constituentVolumes = {}
Internal structure container.
-
bool layerContainer = false
Layer container flag.
-
std::vector<BinningData> constituentBinning = {}
-
struct InternalStructure
- #include <Acts/Detector/ProtoDetector.hpp>
Public Members
-
Surface::SurfaceType layerType = Surface::SurfaceType::Other
Possibility to provide a layer type information.
-
std::vector<BinningData> surfaceBinning = {}
Possibility to provide a surface binning.
-
Surface::SurfaceType layerType = Surface::SurfaceType::Other
-
void constrainDown(const ProtoVolume &ptVolume)
-
class ProtoVolumeMaterial : public Acts::IVolumeMaterial
- #include <Acts/Material/ProtoVolumeMaterial.hpp>
proxy to VolumeMaterial hand over BinUtility
The ProtoVolumeMaterial class acts as a proxy to the VolumeMaterial to mark the volume on which the material should be mapped on at construction time of the geometry and to hand over the granularity of of the material map with the bin Utility.
Public Functions
-
ProtoVolumeMaterial() = default
Constructor without BinUtility - homogeneous material.
-
ProtoVolumeMaterial(const BinUtility &binUtility)
Constructor with BinUtility - multidimensional material.
- Parameters
binUtility – a BinUtility determining the granularity and binning of the material on the volume
-
ProtoVolumeMaterial(const ProtoVolumeMaterial &vmproxy) = default
Copy constructor.
- Parameters
vmproxy – The source proxy
-
ProtoVolumeMaterial(ProtoVolumeMaterial &&vmproxy) = default
Copy move constructor.
- Parameters
vmproxy – The source proxy
-
~ProtoVolumeMaterial() override = default
Destructor.
-
inline const BinUtility &binUtility() const
Return the BinUtility.
Return the bin Utility.
-
ProtoVolumeMaterial &operator=(const ProtoVolumeMaterial &vmproxy) = default
Assignment operator.
- Parameters
vmproxy – The source proxy
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
- Parameters
sl – The outoput stream
-
ProtoVolumeMaterial() = default
-
class RadialBounds : public Acts::DiscBounds
- #include <Acts/Surfaces/RadialBounds.hpp>
Class to describe the bounds for a planar DiscSurface.
By providing an argument for hphisec, the bounds can be restricted to a phi-range around the center position.
Public Types
-
enum BoundValues
Values:
-
enumerator eMinR
-
enumerator eMaxR
-
enumerator eHalfPhiSector
-
enumerator eAveragePhi
-
enumerator eSize
-
enumerator eMinR
Public Functions
-
RadialBounds() = delete
-
inline RadialBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor from array values.
- Parameters
values – The bound values
-
inline RadialBounds(double minR, double maxR, double halfPhi = M_PI, double avgPhi = 0.) noexcept(false)
Constructor for full disc of symmetric disc around phi=0.
- Parameters
minR – The inner radius (0 for full disc)
maxR – The outer radius
halfPhi – The half opening angle (Pi for full angular coverage)
avgPhi – The average phi for the disc/ring sector
-
~RadialBounds() override = default
-
inline virtual double binningValuePhi() const final
Return a reference radius for binning.
-
inline virtual double binningValueR() const final
Return a reference radius for binning.
-
inline virtual bool coversFullAzimuth() const final
Returns true for full phi coverage.
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck) const final
For disc surfaces the local position in (r,phi) is checked.
- Parameters
lposition – local position to be checked
bcheck – boundary check directive
- Returns
is a boolean indicating the operation success
-
inline virtual bool insideRadialBounds(double R, double tolerance = 0.) const final
Checks if this is inside the radial coverage given the a tolerance.
-
inline virtual double rMax() const final
Return method for outer Radius.
-
inline virtual double rMin() const final
Return method for inner Radius.
-
virtual std::ostream &toStream(std::ostream &sl) const final
Outstream operator.
- Parameters
sl – is the ostream to be dumped into
-
virtual SurfaceBounds::BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
enum BoundValues
-
template<typename Type>
class Range1D - #include <Acts/Utilities/Range1D.hpp>
A one-dimensional range between two points.
This type describes a one-demensional range of values, designed to be used in the construction of more complex multi-dimensional types. The class provides functionality for growing and shrinking the range, as well as some other utilities. These ranges are half-open, including the minimum but excluding the maximum.
- Template Parameters
Type – The scalar type of the values contained in this range.
Public Functions
-
inline Range1D()
Construct a new degenerate range object.
This constructor coonstructs a degenerate range object with a maximum lower than the minimum. In other words, this range is empty.
-
inline Range1D(const Range1D<Type> &o)
Construct a new range object from an existing range.
This simply copies the values from the existing range to the new one. It’s the copy constructor.
- Parameters
o – The range to copy
-
inline Range1D(const std::pair<Type, Type> &p)
Construct a new range object from a pair of bounds.
Construct a new range object from a pair of values, the first of which is taken to be the minimum, and the second of which is taken to be the maximum.
- Parameters
p – The pair of values to use as the minimum and maximum
-
inline Range1D(Type min, Type max)
Construct a new range object from a lower and upper bound.
Construct a new range object given the values for the minimum and maximum. Note that it is perfectly possible to construct a degenerate range in this way.
- Parameters
min – The minimum value in the range (inclusive)
max – The maximum value in the range (exclusive)
-
inline bool contains(const Type &v) const
Determine if the range contains a given value.
A value is inside a range if and only if it is greater than the minimum and smaller than the maximum.
- Parameters
v – The value to check
- Returns
true The value is inside the range
- Returns
false The value is not inside the range
-
inline bool degenerate(void) const
Determine if this range is degenerate or not.
A degenerate range has a minimum higher than the maximum, and thus cannot contain any values.
- Returns
true The range is degenerate and has size zero
- Returns
false The range is not degenerate
-
inline void expand(const Type &min, const Type &max)
Expand a range on both ends.
Expand a range by decreasing the minimum value as well as increasing the maximum value. If either of the values are already larger or smaller (respectively) than the proposed values, then that particular boundary of the interval is not expanded.
Note
After this operation, the range is always equal to or larger than [min, max].
- Parameters
min – The proposed new minimum for the range
max – The proposed new maximum for the range
-
inline void expandMax(const Type &v)
Expand a range by increasing the maximum value.
Expand the range by increasing the maximum value. If the given value is smaller than the current maximum (in other words, if the proposed new range would be smaller than the current range), this is a no-op.
- Parameters
v – The proposed new maximum for the range
-
inline void expandMin(const Type &v)
Expand a range by decreasing the minimum value.
Expand the range by decreasing the minimum value. If the given value is larger than the current minimum (in other words, if the proposed new range would be smaller than the current range), this is a no-op.
- Parameters
v – The proposed new minimum for the range
-
inline Type max(void) const
Return the maximum value of the range (inclusive)
-
inline Type min(void) const
Return the minimum value of the range (inclusive)
-
inline Range1D<Type> operator&(const Range1D<Type> &o) const
Compute the intersection of two ranges.
The intersection of two ranges is the range containing all values contained in both ranges. If the two ranges do not intersect, the intersection is a degenerate range. This operation is commutative.
- Parameters
o – The range to compute the intersection with
- Returns
The intersection range between the two ranges
-
inline bool operator&&(const Range1D<Type> &o) const
Determine whether the range intersects another range.
The intersection of a range is the space where both ranges overlap. If the ranges overlap at all, they are said to intersect. This operation is commutative.
- Parameters
o – The other range to check
- Returns
true The ranges intersect
- Returns
false The ranges do not intersect
-
inline Range1D<Type> &operator&=(const Range1D<Type> &o)
Set the range to the intersection of itself and another range.
This is an assignment version of operator&, which updates the range on which it is called to ensure that the new range is the intersection of the old range and the new range.
- Parameters
o – The range to compute the intersection with
- Returns
This object
-
inline bool operator<=(const Range1D<Type> &o) const
Determine whether the left-hand range is a subset of the right-hand range.
A range is a subset of another range if and only if all values contained in the first range are also contained in the second range.
- Parameters
o – The other range to check
- Returns
true The left-hand range is a subset of the right-hand range
- Returns
false The left-hand range is not a subset of the right-hand range
-
inline Range1D<Type> &operator=(const Range1D<Type> &o)
Assignment operator.
Copy the right-hand range into the left-hand range, which means setting the minimum and maximum to equal the minimum and maximum of the right-hand side.
- Parameters
o – The range of values to copy
- Returns
This range
-
inline bool operator==(const Range1D<Type> &o) const
Determine whether the range is equal to another range.
Two ranges are equal if and only if their minima and maxima are the same.
Warning
This method relies on the existence of a well-defined notion of equality for the underlying types. Using this method on floating ranges may have unintended effecrs.
- Parameters
o – The other range to check
- Returns
true The ranges are equal
- Returns
false The ranges are not equal
-
inline bool operator>=(const Range1D<Type> &o) const
Determine whether the left-hand range is a superset of the right-hand range.
A range is a superset of another range if and only if all values contained in the second range are also contained in the first range.
- Parameters
o – The other range to check
- Returns
true The left-hand range is a superset of thr right-hand range
- Returns
false The left-hand range is not a superset of the right-hand range
-
inline void set(const Type &min, const Type &max)
Set the minimum and maximum value.
Override both the minimum and maximum value of the range, regardless of what they were set to.
Note
If you want to shrink or expand the range, use the shrink and expand methods.
Note
After this operation, the range should be exactly equal to [min, max]
- Parameters
min – The new minimum value of the range
max – The new maximum value of the range
-
inline void setMax(const Type &v)
Set the maximum value.
Override the maximum value of the range, regardless of what was already set.
Note
If you want to shrink or expand the range, use the shrink and expand methods.
- Parameters
v – The value to use as the new maximum
-
inline void setMin(const Type &v)
Set the minimum value.
Override the minimum value of the range, regardless of what was already set.
Note
If you want to shrink or expand the range, use the shrink and expand methods.
- Parameters
v – The value to use as the new minimum
-
inline void shrink(const Type &min, const Type &max)
Shrink a range on both ends.
Shrink a range by increasing the minimum value as well as decreasing the maximum value. If either of the values are already smaller or larger (respectively) than the proposed values, then that particular boundary of the interval is not shrunk.
Note
After this operation, the range is always equal to or smaller than [min, max].
- Parameters
min – The proposed new minimum for the range
max – The proposed new maximum for the range
-
inline void shrinkMax(const Type &v)
Shrink a range by decreasing the maximum value.
Shrink the range by decreasing the maximum value. If the given value is larger than the current maximum (in other words, if the proposed new range would be larger than the current range), this is a no-op.
- Parameters
v – The proposed new maximum for the range
-
inline void shrinkMin(const Type &v)
Shrink a range by increasing the minimum value.
Shrink the range by increasing the minimum value. If the given value is smaller than the current minimum (in other words, if the proposed new range would be larger than the current range), this is a no-op.
- Parameters
v – The proposed new minimum for the range
-
inline Type size(void) const
Compute the size of the range.
The size of a range is defined as the difference between the minimum and the maximum. For degenerate ranges, this is zero.
Warning
Due to the nature of numbers, the result of this function can be somewhat ambiguous. For natural numbers, you could argue that the range [n, n] has size 0 or size 1. In this case we say it has size 0. The uncountable nature of the reals means this doesn’t matter for them, but this can be awkward when working with integers.
- Returns
The size of the range
-
template<std::size_t Dims, typename Type, template<typename, std::size_t> typename Vector = std::array>
class RangeXD - #include <Acts/Utilities/RangeXD.hpp>
An orthogonal range in an arbitrary number of dimensions.
By combining a number one-dimensional ranges we can (under the assumption that our axes are orthogonal) construct an orthogonal range of values. In other words, a hyperrectangular volume in space.
- Template Parameters
Dims – The number of dimensions in our range
Type – The scalar type of our ranges
Vector – The vector type used to define coordinates
Public Types
Public Functions
-
inline bool contains(const coordinate_t &v) const
Determine whether the range contains a certain point.
This is true if and only if the range contains the point in all of its dimensions.
- Parameters
v – The coordinate to check for membership in the range
- Returns
true The coordinate is inside the range
- Returns
false The coordinate is outside the range
-
inline bool degenerate(void) const
Determine whether this range is degenerate.
A degenerate multi-dimensional range has no volume and cannot contain any values. This is the case if any of its dimensions are degenerate.
- Returns
true The range is degenerate
- Returns
false The range is not degenerate
-
inline RangeXD<Dims, Type, Vector> operator&(const RangeXD<Dims, Type, Vector> &o) const
Compute the intersection of this range with another range.
The intersection of one orthogonal range with another orthogonal range is in itself an orthogonal range. This operation is commutative. This intersection between two n-dimensional ranges is defined simply as the intersection in each dimension of the two ranges.
- Parameters
o – The orthogonal range to compute the intersection with
- Returns
The intersection between the ranges
-
inline bool operator&&(const RangeXD<Dims, Type, Vector> &r) const
Determine whether this range intersects another.
Two n-dimensional ranges intersect if and only if they intersect in every one of their n dimensions. Otherwise, they are disjoint.
- Parameters
r – The other range to check
- Returns
true The ranges intersect
- Returns
false The ranges do not intersect
-
inline RangeXD<Dims, Type, Vector> &operator&=(const RangeXD<Dims, Type, Vector> &o)
Update the range to the intersection with another range.
This is the assignment version of the operator& method, meaning that it updates the object on which it is called rather than producing a new range.
- Parameters
o – The range to compute the intersection with
- Returns
This object
-
inline bool operator<=(const RangeXD<Dims, Type, Vector> &o) const
Determine whether one range is a subset of another range.
One range is a subset of another range if and only if all points contained within the first set are also contained within the second set. Alternatively, this is equivalent to each of the first range’s one-dimensional ranges being a subset of the second range’s equivalent one-dimensional range.
- Parameters
o – The other range to compare to
- Returns
true The first range is a subset of the second range
- Returns
false The first range is not a subset of the second range
-
inline bool operator==(const RangeXD<Dims, Type, Vector> &o) const
Determine whether two ranges are equal.
Two n-dimensional ranges are equal if and only if they are equal in each of their n dimensions.
- Parameters
o – The other range to check for equality
- Returns
true The ranges are equal
- Returns
false The ranges are not equal
-
inline bool operator>=(const RangeXD<Dims, Type, Vector> &o) const
Determine whether one range is a superset of another range.
One range is a superset of another range if and only if all points contained within the second range are also contained within the first range. Alternatively, this is equivalent to each of the one-dimensional ranges in the first range being a superset of the corresponding one-dimensional range in the second range.
- Parameters
o – The other range to compare to
- Returns
true The left-hand range is a superset of the right-hand range
- Returns
false The left-hand range is not a superset of the right-hand range
-
inline Range1D<Type> &operator[](const std::size_t &i)
Access one of the dimensional ranges of the volume.
- Parameters
i – The index of the dimension to access
- Returns
A reference to the dimension contained in this range
-
inline const Range1D<Type> &operator[](const std::size_t &i) const
Access one of the dimensional ranges of the volume.
- Parameters
i – The index of the dimension to access
- Returns
A reference to the dimension contained in this range
-
inline std::string toString(void) const
Represent the range as a string.
This method produces a helpful string that can be used to debug the range if needed. Not really designed to be used in production code.
- Returns
A string representing the range
-
template<typename value_t, size_t DIM>
class Ray - #include <Acts/Utilities/Ray.hpp>
Class which models a ray.
It is defined by a starting point and a direction.
- Template Parameters
value_t – The floating point type to use
DIM – The number of dimensions in which this ray is defined (2 or 3)
Public Types
-
using value_type = value_t
Re expose the value type.
Public Functions
-
Ray(const VertexType &origin, const VertexType &dir)
Constructor from an origin point and a direction.
- Parameters
origin – The origin of the ray
dir – The direction of the ray
-
inline const VertexType &dir() const
Getter for the direction.
- Returns
The direction
-
template<size_t D = DIM, std::enable_if_t<D == 3, int> = 0>
void draw(IVisualization3D &helper, value_type far_distance = 10) const Helper to draw this ray using a given visualization helper.
- Parameters
helper – The visualization helper
far_distance – The “length” of the drawn line representing the ray
-
inline const vertex_array_type &idir() const
Getter for the element wise inverse of the direction.
- Returns
The element wise inverse.
-
inline const VertexType &origin() const
Getter for the origin.
- Returns
The origin
-
std::ostream &toStream(std::ostream &os) const
Write information on this instance to an outstream.
- Parameters
os – The out stream
- Returns
The out stream given as an argument
-
Ray<value_t, DIM> transformed(const transform_type &trf) const
Transforms this ray using a given transform and returns a new instance.
- Parameters
trf – The transform to apply
- Returns
Copy of this ray with the transform applied
-
struct RecordedMaterial
- #include <Acts/Material/MaterialInteraction.hpp>
Simple result struct to be returned It mainly acts as an internal state which is created for every propagation/extrapolation step.
Public Members
-
double materialInL0 = 0.
The accumulated materialInL0.
-
std::vector<MaterialInteraction> materialInteractions
This one is only filled when recordInteractions is switched on.
-
double materialInX0 = 0.
-
double materialInL0 = 0.
-
class RectangleBounds : public Acts::PlanarBounds
- #include <Acts/Surfaces/RectangleBounds.hpp>
Bounds for a rectangular, planar surface - it can be used to for rectangles that are symmetrically centered around (0.
/0.) and for generic shifted rectangles
Public Types
-
enum BoundValues
Values:
-
enumerator eMinX
-
enumerator eMinY
-
enumerator eMaxX
-
enumerator eMaxY
-
enumerator eSize
-
enumerator eMinX
Public Functions
-
RectangleBounds() = delete
-
inline RectangleBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor - from fixed size array - generic.
- Parameters
values – The parameter values
-
inline RectangleBounds(const Vector2 &min, const Vector2 &max) noexcept(false)
Constructor - from min/max - generic.
- Parameters
min – The left bottom corner
max – The right top corning
-
inline RectangleBounds(double halfX, double halfY) noexcept(false)
Constructor with halflength in x and y - symmetric.
- Parameters
halfX – halflength in X
halfY – halflength in Y
-
~RectangleBounds() override = default
-
virtual const RectangleBounds &boundingBox() const final
Bounding box parameters.
- Returns
rectangle bounds for a bounding box
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
inline double halfLengthX() const
Access to the half length in X.
-
inline double halfLengthY() const
Access to the half length in Y.
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck) const final
Inside check for the bounds object driven by the boundary check directive Each Bounds has a method inside, which checks if a LocalPosition is inside the bounds Inside can be called without/with tolerances.
- Parameters
lposition – Local position (assumed to be in right surface frame)
bcheck – boundary check directive
- Returns
boolean indicator for the success of this operation
-
inline const Vector2 &max() const
Get the max vertex defining the bounds.
- Returns
The max vertex
-
inline const Vector2 &min() const
Get the min vertex defining the bounds.
- Returns
The min vertex
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
- Parameters
sl – is the ostream for the dump
-
inline virtual BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Access method for bound values, this is a dynamically sized vector containing the parameters needed to describe these bounds.
- Returns
of the stored values for this SurfaceBounds object
-
virtual std::vector<Vector2> vertices(unsigned int lseg = 1) const final
Return the vertices.
Note
the number of segments is ignored in this representation
- Parameters
lseg – the number of segments used to approximate and eventually curved line
- Returns
vector for vertices in 2D
-
enum BoundValues
-
template<typename T, typename E = std::error_code>
class Result - #include <Acts/Utilities/Result.hpp>
Class which encapsulates either a valid result, or an error.
- Template Parameters
T – The valid result value
E – The error, defaults to
std::error_code
Public Functions
-
Result() = delete
Default construction is disallowed.
-
template<typename T2, typename _E = E, typename _T = T, typename = std::enable_if_t<(!std::is_same_v<_T, _E> && !std::is_constructible_v<_T, _E> && !std::is_convertible_v<_T, _E> && !std::is_constructible_v<_E, _T> && !std::is_convertible_v<_E, _T> && !(std::is_convertible_v<T2, _T> && std::is_convertible_v<T2, _E>))>>
inline Result(T2 value) noexcept Constructor from arbitrary value This constructor allows construction from any value.
This constructor is only enabled if T and E are unambiguous, meaning the cannot be implicitly converted and there is T cannot be constructed from E and vice-versa. This means that when this is invoked, the value can be propagated to the underlying variant, and the assignment will be correct, and error will be an error, and a value will be a value.
Note
If T and E are ambiguous, use the
successandfailurestatic factory methods.- Template Parameters
T2 – Type of the potential assignment
- Parameters
value – The potential value, could be an actual valid value or an error.
-
inline E error() && noexcept
Returns the error by-value.
Note
If
res.ok()this method will abort (noexcept)- Returns
The error
-
inline E &error() & noexcept
Returns a reference to the error stored in the result.
Note
If
res.ok()this method will abort (noexcept)- Returns
Reference to the error
-
inline bool ok() const noexcept
Checks whether this result contains a valid value, and no error.
- Returns
bool Whether result contains an error or not.
-
inline T &operator*() noexcept
Returns a reference into the variant to the valid value.
Note
If
!res.ok(), this method will abort (noexcept)- Returns
Reference to value stored in the variant.
-
inline T *operator->() noexcept
Allows to access members of the stored object with
res->foosimilar tostd::optional.Note
If
!res.ok(), this method will abort (noexcept)- Returns
Pointer to value stored in the variant.
-
inline Result<T, E> &operator=(Result<T, E> &&other)
Move assignment is allowed.
- Parameters
other – The other result instance, rvalue reference
- Returns
The assigned instance
-
template<typename T2, typename _E = E, typename _T = T, typename = std::enable_if_t<(!std::is_same_v<_T, _E> && !std::is_constructible_v<_T, _E> && !std::is_convertible_v<_T, _E> && !std::is_constructible_v<_E, _T> && !std::is_convertible_v<_E, _T> && !(std::is_convertible_v<T2, _T> && std::is_convertible_v<T2, _E>))>>
inline Result<T, E> &operator=(T2 value) noexcept Assignment operator from arbitrary value This operator allows construction from any value.
The same rules as for the
Result(T2 value)constructor apply.- Template Parameters
T2 – Type of the potential assignment
- Parameters
value – The potential value, could be an actual valid value or an error.
- Returns
The assigned instance
-
inline T &value() &
Retrieves the valid value from the result object.
Note
This is the lvalue version, returns a reference to the value
- Returns
The valid value as a reference
-
inline T value() &&
Retrieves the valid value from the result object.
Note
This is the rvalue version, returns the value by-value and moves out of the variant.
- Returns
The valid value by value, moved out of the variant.
-
template<typename E>
class Result<void, E> - #include <Acts/Utilities/Result.hpp>
Template specialization for the void case.
This specialization handles the case where there is no actual return value, but an error might be returned. Returning the error directly would make handling different from other functions using the
Result<T, E>mechanism.Result<void, E>does not have the dereference operator, and value methods. The staticsuccessfactory does not accept a value.Note
To ease usage, this
Result<void, E>is default constructible in the ok state, whereasResult<T, E>is not.- Template Parameters
E – The type of the error
Public Functions
-
Result() = default
Default constructor which initializes the result in the ok state.
-
template<typename E2>
inline Result(E2 error) noexcept Constructor from error.
This implicitly requires E2 to be convertible to E.
- Template Parameters
E2 – The type of the actual error
- Parameters
error – The instance of the actual error
-
inline Result(Result<void, E> &&other)
Move constructor.
- Parameters
other – The other result object, rvalue ref
-
inline E error() && noexcept
Returns the error by-value.
Note
If
res.ok()this method will abort (noexcept)- Returns
Reference to the error
-
inline E &error() & noexcept
Returns a reference to the error stored in the result.
Note
If
res.ok()this method will abort (noexcept)- Returns
Reference to the error
-
inline bool ok() const noexcept
Checks whether this result is in the ok state, and no error.
- Returns
bool Whether result contains an error or not.
-
Result<void, E> &operator=(const Result<void, E> &other) = default
The (self) assignment operator is deleted.
-
template<typename propagator_t>
class RiddersPropagator - #include <Acts/Propagator/RiddersPropagator.hpp>
This class performs the Ridders algorithm to estimate the propagation of the covariance to a certain point in space.
The algorithm is based on the small deviations of the start parameters based on their uncertainty at the beginning of the propgation. This deviation is represented here by a vector of relative deviations of these parameters and fix for all parameters. So, a common choice has to be found that is able to actually fit into the order of magnitude of the uncertainty of each parameter. Using these deviations, the propagation is repeated multiple times and the final covariance matrix at a given target surface is afterwards evaluated by first order derivatives of the final state parameters wrt. the initial parameters. Therefore this evaluation represents a first order approximation of the transport jacobian. Since performing multiple propagations and a numerical evaluation of the covariance requires more time than a single propagation towards a target + a common propagation of the covariance, this class just serves to verify the results of the latter classes.
Public Functions
-
inline RiddersPropagator(propagator_t &propagator, Config config = {})
Constructor using a propagator.
- Parameters
propagator – [in] Underlying propagator that will be used
config – [in] Config for the Ridders propagation
Constructor building a propagator.
- Template Parameters
stepper_t – Type of the stepper
navigator_t – Type of the navigator
- Parameters
stepper – [in] Stepper that will be used
navigator – [in] Navigator that will be used
config – [in] Config for the Ridders propagation
-
template<typename parameters_t, typename propagator_options_t>
Result<action_list_t_result_t<CurvilinearTrackParameters, typename propagator_options_t::action_list_type>> propagate(const parameters_t &start, const propagator_options_t &options) const Propagation method targeting curvilinear parameters.
- Template Parameters
parameters_t – Type of the start parameters
propagator_options_t – Type of the propagator options
- Parameters
start – [in] Start parameters
options – [in] Options of the propagations
- Returns
Result of the propagation
-
template<typename parameters_t, typename propagator_options_t>
Result<action_list_t_result_t<BoundTrackParameters, typename propagator_options_t::action_list_type>> propagate(const parameters_t &start, const Surface &target, const propagator_options_t &options) const Propagation method targeting bound parameters.
Note
If the target surface is a disc, the resulting covariance may be inconsistent. In this case a zero matrix is returned.
- Template Parameters
parameters_t – Type of the start parameters
propagator_options_t – Type of the propagator options
- Parameters
start – [in] Start parameters
target – [in] The target surface
options – [in] Options of the propagations
- Returns
Result of the propagation
-
struct Config
- #include <Acts/Propagator/RiddersPropagator.hpp>
Public Members
-
std::vector<double> deviations = {-4e-4, -2e-4, 2e-4, 4e-4}
Set of deltas which will be added to the nominal track parameters.
-
std::vector<double> deviationsDisc = {-3e-5, -1e-5, 1e-5, 3e-5}
See
deviations- these are applied for disc surfaces.
-
std::vector<double> deviations = {-4e-4, -2e-4, 2e-4, 4e-4}
-
inline RiddersPropagator(propagator_t &propagator, Config config = {})
-
struct SameSurfaceIntersection
- #include <Acts/Utilities/Intersection.hpp>
Public Functions
-
template<typename intersection_t>
inline bool operator()(const intersection_t &i1, const intersection_t &i2) const comparison operator
This is a struct to pick out intersection with identical surfaces
- Template Parameters
intersection_t – Type of the intersection object
- Parameters
i1 – First intersection to test
i2 – Second intersection to test
-
template<typename intersection_t>
-
template<typename SpacePoint>
class Seed - #include <Acts/Seeding/Seed.hpp>
Public Functions
-
Seed(const Seed&) = default
-
Seed(const SpacePoint &b, const SpacePoint &m, const SpacePoint &u, float vertex, float seedQuality = -std::numeric_limits<float>::infinity())
-
inline float seedQuality() const
-
inline const auto &sp() const
-
inline double z() const
-
Seed(const Seed&) = default
-
struct SeedConfirmationRangeConfig
- #include <Acts/Seeding/SeedConfirmationRangeConfig.hpp>
contains parameters for seed confirmation
Public Members
-
float minImpactSeedConf = 1. * Acts::UnitConstants::mm
-
std::size_t nTopForLargeR = 0
-
std::size_t nTopForSmallR = 0
-
float rMaxSeedConf = std::numeric_limits<float>::max()
-
float seedConfMaxZOrigin = 150. * Acts::UnitConstants::mm
-
float seedConfMinBottomRadius = 60. * Acts::UnitConstants::mm
-
float zMaxSeedConf = std::numeric_limits<float>::max()
-
float zMinSeedConf = std::numeric_limits<float>::lowest()
-
float minImpactSeedConf = 1. * Acts::UnitConstants::mm
-
template<typename external_spacepoint_t>
class SeedFilter - #include <Acts/Seeding/SeedFilter.hpp>
Filter seeds at various stages with the currently available information.
Public Functions
-
SeedFilter() = delete
-
SeedFilter(SeedFilterConfig config, IExperimentCuts<external_spacepoint_t> *expCuts = nullptr)
-
virtual ~SeedFilter() = default
-
virtual void filterSeeds_1SpFixed(Acts::SpacePointData &spacePointData, CandidatesForMiddleSp<const InternalSpacePoint<external_spacepoint_t>> &candidates_collector, std::size_t &numQualitySeeds, std::back_insert_iterator<std::vector<Seed<external_spacepoint_t>>> outIt) const
Filter seeds once all seeds for one middle space point have been created.
- Parameters
spacePointData – Auxiliary variables used by the seeding
candidates_collector – collection of seed candidates
numQualitySeeds – number of high quality seeds in seed confirmation
outIt – Output iterator for the seeds for all seeds with the same middle space point
-
virtual void filterSeeds_1SpFixed(Acts::SpacePointData &spacePointData, std::vector<typename CandidatesForMiddleSp<const InternalSpacePoint<external_spacepoint_t>>::value_type> &candidates, std::size_t &numQualitySeeds, std::back_insert_iterator<std::vector<Seed<external_spacepoint_t>>> outIt) const
Filter seeds once all seeds for one middle space point have been created.
- Parameters
spacePointData – Auxiliary variables used by the seeding
candidates – collection of seed candidates
numQualitySeeds – number of high quality seeds in seed confirmation
outIt – Output iterator for the seeds for all seeds with the same middle space point
-
virtual void filterSeeds_2SpFixed(Acts::SpacePointData &spacePointData, const InternalSpacePoint<external_spacepoint_t> &bottomSP, const InternalSpacePoint<external_spacepoint_t> &middleSP, const std::vector<const InternalSpacePoint<external_spacepoint_t>*> &topSpVec, const std::vector<float> &invHelixDiameterVec, const std::vector<float> &impactParametersVec, SeedFilterState &seedFilterState, CandidatesForMiddleSp<const InternalSpacePoint<external_spacepoint_t>> &candidates_collector) const
Create InternalSeeds for the all seeds with the same bottom and middle space point and discard all others.
- Parameters
spacePointData – Auxiliary variables used by the seeding
bottomSP – fixed bottom space point
middleSP – fixed middle space point
topSpVec – vector containing all space points that may be compatible with both bottom and middle space point
invHelixDiameterVec – vector containing 1/(2*r) values where r is the helix radius
impactParametersVec – vector containing the impact parameters
seedFilterState – holds quantities used in seed filter
candidates_collector – container for the seed candidates
-
inline const IExperimentCuts<external_spacepoint_t> *getExperimentCuts() const
-
inline const SeedFilterConfig getSeedFilterConfig() const
-
SeedFilter() = delete
-
struct SeedFilterConfig
- #include <Acts/Seeding/SeedFilterConfig.hpp>
Public Functions
-
inline SeedFilterConfig toInternalUnits() const
Public Members
-
SeedConfirmationRangeConfig centralSeedConfirmationRange
-
size_t compatSeedLimit = 2
-
float compatSeedWeight = 200.
-
float deltaInvHelixDiameter = 0.00003 * 1. / Acts::UnitConstants::mm
-
float deltaRMin = 5. * Acts::UnitConstants::mm
-
SeedConfirmationRangeConfig forwardSeedConfirmationRange
-
float impactWeightFactor = 1.
-
bool isInInternalUnits = false
-
std::size_t maxQualitySeedsPerSpMConf = std::numeric_limits<std::size_t>::max()
-
unsigned int maxSeedsPerSpM = 10
-
std::size_t maxSeedsPerSpMConf = std::numeric_limits<std::size_t>::max()
-
float numSeedIncrement = std::numeric_limits<float>::infinity()
-
bool seedConfirmation = false
-
float seedWeightIncrement = 0
-
bool useDeltaRorTopRadius = false
-
float zOriginWeightFactor = 1.
-
inline SeedFilterConfig toInternalUnits() const
-
struct SeedFilterState
- #include <Acts/Seeding/SeedFilter.hpp>
Public Members
-
size_t nTopSeedConf = 0
-
std::size_t numQualitySeeds = 0
-
std::size_t numSeeds = 0
-
float rMaxSeedConf = std::numeric_limits<float>::max()
-
float zOrigin = 0
-
size_t nTopSeedConf = 0
-
template<typename external_spacepoint_t, typename platform_t = void*>
class SeedFinder - #include <Acts/Seeding/SeedFinder.hpp>
Disallow default instantiation, copy, assignment
-
SeedFinder() = default
-
SeedFinder(const SeedFinder<external_spacepoint_t, platform_t>&) = delete
-
SeedFinder<external_spacepoint_t, platform_t> &operator=(const SeedFinder<external_spacepoint_t, platform_t>&) = default
-
template<template<typename...> typename container_t, typename sp_range_t>
void createSeedsForGroup(const Acts::SeedFinderOptions &options, SeedingState &state, const Acts::SpacePointGrid<external_spacepoint_t> &grid, std::back_insert_iterator<container_t<Seed<external_spacepoint_t>>> outIt, const sp_range_t &bottomSPs, const std::size_t middleSPs, const sp_range_t &topSPs, const Acts::Range1D<float> &rMiddleSPRange) const Create all seeds from the space points in the three iterators.
Can be used to parallelize the seed creation
Note
Ranges must return pointers.
Note
Ranges must be separate objects for each parallel call.
- Parameters
options – frequently changing configuration (like beam position)
state – State object that holds memory used
grid – The grid with space points
outIt – Output iterator for the seeds in the group
bottomSPs – group of space points to be used as innermost SP in a seed.
middleSPs – group of space points to be used as middle SP in a seed.
topSPs – group of space points to be used as outermost SP in a seed.
rMiddleSPRange – range object containing the minimum and maximum r for middle SP for a certain z bin.
-
template<typename sp_range_t>
std::vector<Seed<external_spacepoint_t>> createSeedsForGroup(const Acts::SeedFinderOptions &options, const Acts::SpacePointGrid<external_spacepoint_t> &grid, const sp_range_t &bottomSPs, const std::size_t middleSPs, const sp_range_t &topSPs) const Compatibility method for the new-style seed finding API.
This method models the old-style seeding API where we only need a container for the bottom, middle, and top space points. Also, the results are returned by value instead of inserted into an inserter.
Note
This method is a very simply wrapper around the more modern API.
Warning
The performance of the seeding code is far greater if the new API is used, and this is recommended for all new uses which do not require backwards-compatibility.
- Template Parameters
sp_range_t – container type for the seed point collections.
- Parameters
options – frequently changing configuration (like beam position)
grid – The grid with space points
bottomSPs – group of space points to be used as innermost SP in a seed.
middleSPs – group of space points to be used as middle SP in a seed.
topSPs – group of space points to be used as outermost SP in a seed.
- Returns
a vector of seeds.
Public Functions
-
SeedFinder(const Acts::SeedFinderConfig<external_spacepoint_t> &config)
The only constructor.
Requires a config object.
- Parameters
config – the configuration for the SeedFinder
-
~SeedFinder() = default
-
struct SeedingState
- #include <Acts/Seeding/SeedFinder.hpp>
Public Members
-
boost::container::small_vector<Acts::Neighbour<external_spacepoint_t>, 9> bottomNeighbours
-
CandidatesForMiddleSp<const InternalSpacePoint<external_spacepoint_t>> candidates_collector
-
std::vector<InternalSpacePoint<external_spacepoint_t>*> compatBottomSP
-
std::vector<InternalSpacePoint<external_spacepoint_t>*> compatTopSP
-
std::vector<float> curvatures
-
std::vector<float> impactParameters
-
std::vector<LinCircle> linCircleBottom
-
std::vector<LinCircle> linCircleTop
-
Acts::SpacePointData spacePointData
-
boost::container::small_vector<Acts::Neighbour<external_spacepoint_t>, 9> topNeighbours
-
std::vector<const InternalSpacePoint<external_spacepoint_t>*> topSpVec
-
boost::container::small_vector<Acts::Neighbour<external_spacepoint_t>, 9> bottomNeighbours
-
SeedFinder() = default
-
template<typename SpacePoint>
struct SeedFinderConfig - #include <Acts/Seeding/SeedFinderConfig.hpp>
Public Functions
-
inline SeedFinderConfig calculateDerivedQuantities() const
-
inline SeedFinderConfig toInternalUnits() const
Public Members
-
float binSizeR = 1. * Acts::UnitConstants::mm
-
SeedConfirmationRangeConfig centralSeedConfirmationRange
-
float collisionRegionMax = +150 * Acts::UnitConstants::mm
-
float collisionRegionMin = -150 * Acts::UnitConstants::mm
-
float cotThetaMax = 7.40627
-
float deltaRMax = 270 * Acts::UnitConstants::mm
-
float deltaRMaxBottomSP = std::numeric_limits<float>::quiet_NaN()
-
float deltaRMaxTopSP = std::numeric_limits<float>::quiet_NaN()
-
float deltaRMiddleMaxSPRange = 10. * Acts::UnitConstants::mm
-
float deltaRMiddleMinSPRange = 10. * Acts::UnitConstants::mm
-
float deltaRMin = 5 * Acts::UnitConstants::mm
-
float deltaRMinBottomSP = std::numeric_limits<float>::quiet_NaN()
-
float deltaRMinTopSP = std::numeric_limits<float>::quiet_NaN()
-
float deltaZMax = std::numeric_limits<float>::infinity() * Acts::UnitConstants::mm
-
SeedConfirmationRangeConfig forwardSeedConfirmationRange
-
Delegate<float(const SpacePoint&)> getBottomHalfStripLength
-
Delegate<Acts::Vector3(const SpacePoint&)> getBottomStripDirection
-
Delegate<Acts::Vector3(const SpacePoint&)> getStripCenterDistance
-
Delegate<float(const SpacePoint&)> getTopHalfStripLength
-
Delegate<Acts::Vector3(const SpacePoint&)> getTopStripCenterPosition
-
Delegate<Acts::Vector3(const SpacePoint&)> getTopStripDirection
-
float highland = 0
-
float impactMax = 20. * Acts::UnitConstants::mm
-
bool interactionPointCut = false
-
bool isInInternalUnits = false
-
int maxBlockSize = 1024
-
float maxPtScattering = 10 * Acts::UnitConstants::GeV
-
float maxScatteringAngle2 = 0
-
unsigned int maxSeedsPerSpM = 5
-
float minPt = 400. * Acts::UnitConstants::MeV
-
int nAvgTrplPerSpBLimit = 2
-
int nTrplPerSpBLimit = 100
-
float phiMax = M_PI
-
float phiMin = -M_PI
-
float radLengthPerSeed = 0.05
-
float rAlign = 0 * Acts::UnitConstants::mm
-
float rMax = 600 * Acts::UnitConstants::mm
-
float rMaxMiddle = 120.f * Acts::UnitConstants::mm
-
float rMin = 33 * Acts::UnitConstants::mm
-
float rMinMiddle = 60.f * Acts::UnitConstants::mm
-
std::vector<std::vector<float>> rRangeMiddleSP
-
bool seedConfirmation = false
-
std::shared_ptr<Acts::SeedFilter<SpacePoint>> seedFilter
-
float sigmaError = 5
-
float sigmaScattering = 5
-
std::size_t skipZMiddleBinSearch = 0
-
float toleranceParam = 1.1 * Acts::UnitConstants::mm
-
bool useDetailedDoubleMeasurementInfo = false
-
bool useVariableMiddleSPRange = false
-
float zAlign = 0 * Acts::UnitConstants::mm
-
std::vector<float> zBinEdges
-
std::vector<size_t> zBinsCustomLooping = {}
-
float zMax = 2800 * Acts::UnitConstants::mm
-
float zMin = -2800 * Acts::UnitConstants::mm
-
std::pair<float, float> zOutermostLayers = {-2700 * Acts::UnitConstants::mm, 2700 * Acts::UnitConstants::mm}
-
inline SeedFinderConfig calculateDerivedQuantities() const
-
struct SeedFinderOptions
- #include <Acts/Seeding/SeedFinderConfig.hpp>
Public Functions
-
template<typename Config>
inline SeedFinderOptions calculateDerivedQuantities(const Config &config) const
-
inline SeedFinderOptions toInternalUnits() const
Public Members
-
Acts::Vector2 beamPos = {0 * Acts::UnitConstants::mm, 0 * Acts::UnitConstants::mm}
-
float bFieldInZ = 2.08 * Acts::UnitConstants::T
-
bool isInInternalUnits = false
-
float minHelixDiameter2 = std::numeric_limits<float>::quiet_NaN()
-
float multipleScattering2 = std::numeric_limits<float>::quiet_NaN()
-
float pT2perRadius = std::numeric_limits<float>::quiet_NaN()
-
float pTPerHelixRadius = std::numeric_limits<float>::quiet_NaN()
-
float sigmapT2perRadius = std::numeric_limits<float>::quiet_NaN()
-
template<typename Config>
-
template<typename external_spacepoint_t>
class SeedFinderOrthogonal - #include <Acts/Seeding/SeedFinderOrthogonal.hpp>
Public Types
-
using internal_sp_t = InternalSpacePoint<external_spacepoint_t>
The spacepoint type used by this seeder internally.
-
using seed_t = Seed<external_spacepoint_t>
The seed type used by this seeder internally.
-
using tree_t = KDTree<NDims, internal_sp_t*, ActsScalar, std::array, 4>
The k-d tree type used by this seeder internally, which is three-dimensional, contains internal spacepoint pointers, uses the Acts scalar type for coordinates, stores its coordinates in std::arrays, and has leaf size 4.
Public Functions
-
SeedFinderOrthogonal() = default
-
SeedFinderOrthogonal(const Acts::SeedFinderOrthogonalConfig<external_spacepoint_t> &config)
Construct a new orthogonal seed finder.
- Parameters
config – The configuration parameters for this seed finder.
-
SeedFinderOrthogonal(const SeedFinderOrthogonal<external_spacepoint_t>&) = delete
-
~SeedFinderOrthogonal() = default
Destroy the orthogonal seed finder object.
-
template<typename input_container_t, typename callable_t>
std::vector<seed_t> createSeeds(const Acts::SeedFinderOptions &options, const input_container_t &spacePoints, callable_t &&extract_coordinates) const Perform seed finding, returning a new container of seeds.
This is a filterCandidates method for scenarios where a non-inserter API is more ergonomic. In general, the inserter-based method should be preferred as it is more flexible and usually more performant. For more information about the seeding algorithm, please see that function.
- Template Parameters
input_container_t – The type of the input spacepoint container.
- Parameters
options – frequently changing configuration (like beam position)
spacePoints – The input spacepoints from which to create seeds.
extract_coordinates – User-defined function for extracting global position and covariance of the external space point
- Returns
A vector of seeds.
-
template<typename input_container_t, typename output_container_t, typename callable_t>
void createSeeds(const Acts::SeedFinderOptions &options, const input_container_t &spacePoints, output_container_t &out_cont, callable_t &&extract_coordinates) const Perform seed finding, appending seeds to a container.
This method performs seed finding through an orthogonal range search strategy. This strategy differs from binning approaches because it selects seeds constructively rather than destructively; instead of trying a large number of possible space point combinations and then rejecting many of them, this algorithm tries to only consider valid seed candidates to reduce combinatorics.
In addition, this algorithm replaces the binning step used in other seed finding algorithms with the construction of a k-d tree, which allows us to efficiently search for space points within a given range.
The core idea behind this algorithm is to create axis-aligned bounding boxes around the region of validity for a seed candidate (be it a bottom spacepoint for a given middle, a top for a given middle, a middle for a given bottom, or any other combination), and then searching the detector volume for points that lie inside that AABB.
- Template Parameters
input_container_t – The type of the input spacepoint container.
output_container_t – The type of the output seed container.
- Parameters
options – frequently changing configuration (like beam position)
spacePoints – The input spacepoints from which to create seeds.
out_cont – The output container to write seeds to.
extract_coordinates – User-defined function for extracting global position and covariance of the external space point
-
SeedFinderOrthogonal<external_spacepoint_t> &operator=(const SeedFinderOrthogonal<external_spacepoint_t>&) = default
Public Static Attributes
-
static constexpr std::size_t NDims = 3
Set the number of dimensions in which to embed points.
This is just 3 for now (phi, r, and z), but we might want to increase or decrease this number in the future.
-
using internal_sp_t = InternalSpacePoint<external_spacepoint_t>
-
template<typename SpacePoint>
struct SeedFinderOrthogonalConfig - #include <Acts/Seeding/SeedFinderOrthogonalConfig.hpp>
Public Functions
-
inline SeedFinderOrthogonalConfig calculateDerivedQuantities() const
-
inline SeedFinderOrthogonalConfig toInternalUnits() const
Public Members
-
SeedConfirmationRangeConfig centralSeedConfirmationRange
-
float collisionRegionMax = +150 * Acts::UnitConstants::mm
-
float collisionRegionMin = -150 * Acts::UnitConstants::mm
-
float cotThetaMax = 7.40627
-
float deltaPhiMax = 0.085
-
float deltaRMaxBottomSP = 270 * Acts::UnitConstants::mm
-
float deltaRMaxTopSP = 270 * Acts::UnitConstants::mm
-
float deltaRMiddleMaxSPRange = 10. * Acts::UnitConstants::mm
-
float deltaRMiddleMinSPRange = 10. * Acts::UnitConstants::mm
-
float deltaRMinBottomSP = 5 * Acts::UnitConstants::mm
-
float deltaRMinTopSP = 5 * Acts::UnitConstants::mm
-
float deltaZMax = std::numeric_limits<float>::infinity() * Acts::UnitConstants::mm
-
SeedConfirmationRangeConfig forwardSeedConfirmationRange
-
float highland = 0
-
float impactMax = 20. * Acts::UnitConstants::mm
-
bool interactionPointCut = false
-
bool isInInternalUnits = false
-
float maxPtScattering = 10 * Acts::UnitConstants::GeV
-
float maxScatteringAngle2 = 0
-
unsigned int maxSeedsPerSpM = 5
-
float minPt = 400. * Acts::UnitConstants::MeV
-
float phiMax = M_PI
-
float phiMin = -M_PI
-
float radLengthPerSeed = 0.05
-
float rMax = 600 * Acts::UnitConstants::mm
-
float rMaxMiddle = 120.f * Acts::UnitConstants::mm
-
float rMin = 33 * Acts::UnitConstants::mm
-
float rMinMiddle = 60.f * Acts::UnitConstants::mm
-
std::vector<std::vector<float>> rRangeMiddleSP
-
bool seedConfirmation = false
-
std::shared_ptr<Acts::SeedFilter<SpacePoint>> seedFilter
-
float sigmaScattering = 5
-
bool useVariableMiddleSPRange = true
-
float zMax = 2800 * Acts::UnitConstants::mm
-
float zMin = -2800 * Acts::UnitConstants::mm
-
std::pair<float, float> zOutermostLayers = {-2700 * Acts::UnitConstants::mm, 2700 * Acts::UnitConstants::mm}
-
inline SeedFinderOrthogonalConfig calculateDerivedQuantities() const
-
class Segmentation
- #include <Acts/Digitization/Segmentation.hpp>
Segmentation Base class.
This helper class allows to define an arbitrary readout segmentation for the geoemtric digitization, provided a shape of the module, it creates the segmentation surfaces and hands them to the digitization module
Since the segmentation description might be identical for many elements while the lorentz angle may change, lorentzAngle and readoutDirection are provided and th the segmenation class only creates the surfaces for the module, but hosts the binning information.
Subclassed by Acts::CartesianSegmentation
Public Functions
-
virtual ~Segmentation() = default
Virtual Destructor.
-
virtual const BinUtility &binUtility() const = 0
return the bin utility that defines the readout
-
virtual DigitizationCell cell(const Vector2 &position) const = 0
Get the digitization cell from a 2D position.
ignores the shift, i.e. assumenes in to be in cell frame
- Parameters
position – is the position for which the cell is requested
- Returns
is a cell with cell ids
-
virtual DigitizationCell cell(const Vector3 &position) const = 0
Get the digitization cell from a 3D position.
ignores the shift, i.e. assumenes in to be in cell frame
- Parameters
position – is the position for which the cell is requested
- Returns
is a cell with cell ids
-
virtual Vector2 cellPosition(const DigitizationCell &dCell) const = 0
Calculate the cell Position from the Id.
- Parameters
dCell – the digitization cell
- Returns
the center position of the associated cell
-
virtual void createSegmentationSurfaces(SurfacePtrVector &boundarySurfaces, SurfacePtrVector &segmentationSurfacesX, SurfacePtrVector &segmentationSurfacesY, double halfThickness, int readoutDirection, double lorentzAngle) const = 0
Create the segmentation surfaces in X.
This method is only used if the full 3D digitization is done
- Parameters
boundarySurfaces – vector to be filled
segmentationSurfacesX – are the segmetation boundaries in X
segmentationSurfacesY – are the segmetation boundaries in Y
halfThickness – is the half thickness in z of the module
readoutDirection – is the direction w.r.t normal vector where the readout is given : -1, 0, 1 possible
lorentzAngle – is the lorentz angle measured from the local z towards x axis
-
virtual DigitizationStep digitizationStep(const Vector3 &start, const Vector3 &end, double halfThickness, int readoutDirection, double lorentzAngle) const = 0
Fill the associated digitization cell from the start and end position in 3D correct for lorentz effect if needed.
- Parameters
start – is the start position of the step
end – is the end position of the step
halfThickness – is the half thickness in z
readoutDirection – is the readout direction with respect to local z
lorentzAngle – is the lorentz angle measured from local z towards x
- Returns
is a fully calculated digitzation step
-
virtual const SurfaceBounds &moduleBounds() const = 0
return the surface bounds by reference
-
virtual ~Segmentation() = default
-
template<typename spacepoint_t>
class SingleSeedVertexFinder - #include <Acts/Vertexing/SingleSeedVertexFinder.hpp>
Implements the vertex finder based on the track seeds 0.
Assumes there is only 1 vertex and that it has a high multiplicity
Sorts out all the input spacepoints based on their distance to the z-axis
Create seeds from 3 spacepoints with a small deviation from a straigh line
Find a point with a minimal distance from either planes (minimalizeWRT=”planes”) or rays (minimalizeWRT=”rays”) defined by the the seeds
Returns the point position as the vertex
Public Functions
-
SingleSeedVertexFinder(const Config &cfg, std::unique_ptr<const Logger> lgr = getDefaultLogger("SingleSeedVertexFinder", Logging::INFO))
Constructor.
- Parameters
cfg – Configuration object
lgr – Logging instance
-
~SingleSeedVertexFinder() = default
Destructor.
-
inline const Config &config() const
Const access to the config.
-
Acts::Result<Acts::Vector3> findVertex(const std::vector<spacepoint_t> &spacepoints) const
Finds the vertex based on the provided spacepoints.
- Parameters
spacepoints – Vector of the input spacepoints; they do not need to be sorted anyhow
- Returns
Position of the vertex
-
struct Config
- #include <Acts/Vertexing/SingleSeedVertexFinder.hpp>
Configuration struct.
Public Members
-
Acts::ActsScalar maxAbsZ = 450. * Acts::UnitConstants::mm
maximum |z| to consider, z slices will be done within the range (-maxAbsZ,maxAbsZ) values of maxAbsZ, maxZPosition, rMaxFar, and minTheta should be set reasonably with respect to each other
-
std::uint32_t maxIterations = 20
maximum number of iterations when discarding triplets with the largest chi^2
-
Acts::ActsScalar maxPhideviation = 0.08
maximum deviation in phi between the near and middle spacepoints or middle and far spacepoints
-
Acts::ActsScalar maxRPosition = 10.f * Acts::UnitConstants::mm
maximum R position of the vertex at the point closest to the Z axis
-
Acts::ActsScalar maxXYdeviation = 0.08
maximum deviation in X-Y between the first 2 spacepoints and the last 2 spacepoints
-
Acts::ActsScalar maxXYZdeviation = 0.08
maximum deviation in 3D between the first 2 spacepoints and the last 2 spacepoints
-
Acts::ActsScalar maxZPosition = 200.f * Acts::UnitConstants::mm
maximum Z position of the vertex at the point closest to the Z axis
-
std::string minimalizeWRT = "planes"
chi^2 minimalization will happen with respect to “planes” or “rays”
-
Acts::ActsScalar minTheta = 1.
minimum angle between Z axis and a triplet, effectively removing triplets with large |eta|
-
Acts::ActsScalar minVtxShift = 0.3f * Acts::UnitConstants::mm
if the vertex estimation moves less than this, stop iterations
-
std::uint32_t numPhiSlices = 60
number of phi slices, at least 3 to avoid duplicities it should be less than 2*pi/maxPhideviation in order not to loop over triplets that will be rejected by maxPhideviation anyway
-
std::uint32_t numZSlices = 150
number of z slices
-
Acts::ActsScalar removeFraction = 0.10
each iteration, discard this fraction of triplets with the largest chi^2
-
Acts::ActsScalar rMaxFar = 320.f * Acts::UnitConstants::mm
-
Acts::ActsScalar rMaxMiddle = 190.f * Acts::UnitConstants::mm
-
Acts::ActsScalar rMaxNear = 60.f * Acts::UnitConstants::mm
-
Acts::ActsScalar rMinFar = 280.f * Acts::UnitConstants::mm
-
Acts::ActsScalar rMinMiddle = 150.f * Acts::UnitConstants::mm
-
Acts::ActsScalar rMinNear = 20.f * Acts::UnitConstants::mm
thresholds for near, middle, and far spacepoints
-
Acts::ActsScalar useFracPhiSlices = 0.5
use only a fraction of available phi slices to speed up calculations;
-
Acts::ActsScalar useFracZSlices = 0.5
use only a fraction of available z slices to speed up calculations;
-
Acts::ActsScalar maxAbsZ = 450. * Acts::UnitConstants::mm
-
struct SinglyCharged
- #include <Acts/EventData/Charge.hpp>
Charge and momentum interpretation for particles with +-e charge.
Public Functions
-
constexpr SinglyCharged() = default
-
inline constexpr SinglyCharged(float absQ) noexcept
Construct and verify the input charge magnitude (in debug builds).
This constructor is only provided to allow consistent construction.
-
inline constexpr float absQ() const noexcept
-
template<typename T>
inline constexpr auto extractCharge(T qOverP) const noexcept
-
template<typename T>
inline constexpr auto extractMomentum(T qOverP) const noexcept
Friends
- inline friend constexpr friend bool operator== (SinglyCharged, SinglyCharged) noexcept
Compare for equality.
This is always
trueasSinglyChargedhas no internal state. Must be available to provide a consistent interface.
-
constexpr SinglyCharged() = default
-
class SinglyChargedParticleHypothesis : public Acts::GenericParticleHypothesis<SinglyCharged>
- #include <Acts/EventData/ParticleHypothesis.hpp>
Specialized particle hypothesis for singly charged particles.
Note
This serves as a factory for common singly charge particles.
Public Functions
-
template<typename other_charge_t>
inline constexpr SinglyChargedParticleHypothesis(const GenericParticleHypothesis<other_charge_t> &other)
-
inline SinglyChargedParticleHypothesis(PdgParticle absPdg)
-
inline constexpr SinglyChargedParticleHypothesis(PdgParticle absPdg, float mass)
Public Static Functions
-
static inline SinglyChargedParticleHypothesis electron()
-
static inline SinglyChargedParticleHypothesis muon()
-
static inline SinglyChargedParticleHypothesis pion()
-
template<typename other_charge_t>
-
class SolenoidBField : public Acts::MagneticFieldProvider
- #include <Acts/MagneticField/SolenoidBField.hpp>
Implements a multi-coil solenoid magnetic field.
On every call, the field is evaluated at that exact position. The field has radially symmetry, the field vectors point in +z direction. The config exposes a target field value in the center. This value is used to empirically determine a scale factor which reproduces this field value in the center.
E_1(k^2) = complete elliptic integral of the 1st kind E_2(k^2) = complete elliptic integral of the 2nd kind
E_1(k^2) and E_2(k^2) are usually indicated as K(k^2) and E(k^2) in literature, respectively _ 2 / pi / 2 2 2 - 1 / 2 E (k ) = | ( 1 - k sin {theta} ) dtheta 1 _/ 0
2 / pi / 2| / 2 2 E (k ) = | |/ 1 - k sin {theta} dtheta 2 _/ 0_ ____________________
k^2 = is a function of the point (r, z) and of the radius of the coil R
2 4Rr k = ————— 2 2 (R + r) + z Using these, you can evaluate the two components B_r and B_z of the magnetic field: _ _ mu I | / 2 \ | 0 kz | |2 - k | 2 2 | B (r, z) = –— —— | |—-—|E (k ) - E (k ) | r 4pi ___ | | 2| 2 1 | | / 3 |_ \2 - 2k / _| |/ Rr
mu I | / 2 \ | 0 k | | (R + r)k - 2r | 2 2 | B (r,z) = –— -— | | ———–— | E (k ) + E (k ) | z 4pi __ | | 2 | 2 1 | |/Rr |_ \ 2r(1 - k ) / _|_ _
Public Functions
-
SolenoidBField(Config config)
the constructor with a shared pointer
Note
since it is a shared field, we enforce it to be const
- Template Parameters
bField – is the shared BField to be stored
-
Vector2 getField(const Vector2 &position) const
Retrieve magnetic field value in local (r,z) coordinates.
- Parameters
position – [in] local 2D position
-
Vector3 getField(const Vector3 &position) const
Get the B field at a position.
- Parameters
position – The position to query at
-
virtual Result<Vector3> getField(const Vector3 &position, MagneticFieldProvider::Cache &cache) const override
Retrieve magnetic field value at a given location.
Requires a cache object created through makeCache().
- Parameters
position – [in] global 3D position for the lookup
cache – [inout] Field provider specific cache object
- Returns
magnetic field vector at given position
-
virtual Result<Vector3> getFieldGradient(const Vector3 &position, ActsMatrix<3, 3> &derivative, MagneticFieldProvider::Cache &cache) const override
Retrieve magnetic field value its its gradient.
Requires a cache object created through makeCache().
Note
currently the derivative is not calculated
- Parameters
position – [in] global 3D position
derivative – [out] gradient of magnetic field vector as (3x3) matrix
cache – [inout] Field provider specific cache object
- Returns
magnetic field vector
-
virtual MagneticFieldProvider::Cache makeCache(const MagneticFieldContext &mctx) const override
Make an opaque cache for the magnetic field.
Instructs the specific implementation to generate a
Cacheinstance for magnetic field lookup.- Parameters
mctx – The magnetic field context to generate cache for
- Returns
Cache The opaque cache object
-
struct Cache
- #include <Acts/MagneticField/SolenoidBField.hpp>
Public Functions
-
inline Cache(const MagneticFieldContext &mctx)
Constructor with magnetic field context.
- Parameters
mctx – the magnetic field context
-
inline Cache(const MagneticFieldContext &mctx)
-
struct Config
- #include <Acts/MagneticField/SolenoidBField.hpp>
Config struct for the SolenoidBfield.
Public Members
-
double bMagCenter
The target magnetic field strength at the center.
This will be used to scale coefficients
-
double length
Extent of the solenoid in z.
It goes from -length/2 to +length/2 by convention
-
size_t nCoils
The number of coils that make up the solenoid.
-
double radius
Radius at which the coils are located.
-
double bMagCenter
-
SolenoidBField(Config config)
-
class SourceLink
- #include <Acts/EventData/SourceLink.hpp>
Public Functions
-
SourceLink(const SourceLink &other) = default
-
SourceLink(SourceLink &&other) = default
-
template<typename T, typename = std::enable_if_t<!std::is_same_v<std::decay_t<T>, SourceLink>>>
inline explicit SourceLink(T &&upstream) Constructor from concrete sourcelink.
- Template Parameters
T – The source link type
- Parameters
upstream – The upstream source link to store
-
template<typename T>
inline T &get() Concrete source link class getter.
- Template Parameters
T – The source link type to retrieve
- Returns
Reference to the stored source link
-
template<typename T>
inline const T &get() const Concrete source link class getter, const version.
- Template Parameters
T – The source link type to retrieve
- Returns
Const reference to the stored source link
-
SourceLink &operator=(const SourceLink &other) = default
-
SourceLink &operator=(SourceLink &&other) = default
-
SourceLink(const SourceLink &other) = default
-
template<typename T>
struct SourceLinkAdapterIterator - #include <Acts/EventData/SourceLink.hpp>
Public Types
-
using BaseIterator = T
-
using difference_type = typename BaseIterator::difference_type
-
using iterator_category = typename BaseIterator::iterator_category
-
using pointer = typename BaseIterator::pointer
-
using reference = typename BaseIterator::reference
-
using value_type = typename BaseIterator::value_type
Public Functions
-
inline explicit SourceLinkAdapterIterator(T iterator)
-
inline bool operator!=(const SourceLinkAdapterIterator &other) const
-
inline Acts::SourceLink operator*() const
-
inline SourceLinkAdapterIterator &operator++()
-
inline auto operator-(const SourceLinkAdapterIterator &other) const
-
inline bool operator==(const SourceLinkAdapterIterator &other) const
Public Members
-
BaseIterator m_iterator
-
using BaseIterator = T
-
template<typename spacepoint_t>
class SpacePointBuilder - #include <Acts/SpacePointFormation/SpacePointBuilder.hpp>
After the particle interaction with surfaces are recorded and digitized measurements on the pixel or strip detectors need further treatment.
This class takes the SouceLinks and provides the corresponding space points.
Public Functions
-
SpacePointBuilder() = default
-
SpacePointBuilder(const SpacePointBuilderConfig &cfg, std::function<spacepoint_t(Acts::Vector3, Acts::Vector2, boost::container::static_vector<SourceLink, 2>)> func, std::unique_ptr<const Logger> logger = getDefaultLogger("SpamcePointBuilder", Logging::INFO))
- Parameters
cfg – The configuration for the space point builder
func – The function that provides user’s SP constructor with global pos, global cov, and sourceLinks.
logger – The logging instance
-
template<template<typename...> typename container_t>
void buildSpacePoint(const GeometryContext &gctx, const std::vector<SourceLink> &sourceLinks, const SpacePointBuilderOptions &opt, std::back_insert_iterator<container_t<spacepoint_t>> spacePointIt) const Calculates the space points out of a given collection of SourceLinks and stores the results.
- Parameters
gctx – The current geometry context object, e.g. alignment
sourceLinks – vector of Sourcelink
opt – option for the space point building. It contains the ends of the strips for strip SP building
spacePointIt – Output iterator for the space point
-
void makeSourceLinkPairs(const GeometryContext &gctx, const std::vector<SourceLink> &slinksFront, const std::vector<SourceLink> &slinksBack, std::vector<std::pair<SourceLink, SourceLink>> &slinkPairs, const StripPairOptions &pairOpt) const
Searches possible combinations of two SourceLinks on different surfaces that may come from the same particles.
- Parameters
gctx – The current geometry context object, e.g. alignment
slinksFront – vector of Sourcelinks on a surface
slinksBack – vector of SoruceLinks on another surface
slinkPairs – storage of the SouceLink pairs
pairOpt – pair maker option with paramCovAccessor
-
SpacePointBuilder() = default
-
struct SpacePointBuilderConfig
- #include <Acts/SpacePointFormation/SpacePointBuilderConfig.hpp>
Public Functions
-
SpacePointBuilderConfig() = default
Public Members
-
SourceLinkSurfaceAccessor slSurfaceAccessor
The accessor to retrieve surfaces from source links.
-
std::shared_ptr<const Acts::TrackingGeometry> trackingGeometry
Tracking geometry.
-
bool usePerpProj = false
Perform the perpendicular projection for space point finding.
-
SpacePointBuilderConfig() = default
-
struct SpacePointBuilderOptions
- #include <Acts/SpacePointFormation/SpacePointBuilderOptions.hpp>
Public Members
- std::function< std::pair< const BoundVector, const BoundSquareMatrix > const SourceLink &)> paramCovAccessor
-
double stripLengthGapTolerance = 0.01
Allowed increase of strip length wrt gaps between strips.
-
double stripLengthTolerance = 0.01
Allowed increase of strip length.
-
Vector3 vertex = {0., 0., 0.}
vertex position
-
class SpacePointData
- #include <Acts/EventData/SpacePointData.hpp>
This class contains auxiliary and mutable data associated to the external space points provided by the customers These variables are used internally by the seeding algorithm, that reads and updates them The variables collected here are also dynamic variables only present for strip space points.
Public Functions
-
SpacePointData() = default
Default constructor.
-
SpacePointData(const SpacePointData &other) = delete
No copies.
-
SpacePointData(SpacePointData &&other) noexcept = default
Move operations.
-
~SpacePointData() = default
Destructor.
-
inline void clear()
clear vectors
-
inline const float &deltaR(std::size_t idx) const
-
inline bool hasDynamicVariable() const
-
SpacePointData &operator=(const SpacePointData &other) = delete
-
SpacePointData &operator=(SpacePointData &&other) noexcept = default
-
inline const float &quality(std::size_t idx) const
Getters.
-
inline void resize(std::size_t n, bool resizeDynamic = false)
Resize vectors.
-
inline void setDeltaR(std::size_t idx, const float &value)
-
inline void setQuality(std::size_t idx, const float &value)
Setters.
-
SpacePointData() = default
-
struct SpacePointGridConfig
- #include <Acts/Seeding/SpacePointGrid.hpp>
Public Functions
-
inline SpacePointGridConfig toInternalUnits() const
Public Members
-
float cotThetaMax = 0
-
float deltaRMax = 0
-
float impactMax = 0
-
bool isInInternalUnits = false
-
int maxPhiBins = 10000
-
float minPt = 0
-
int phiBinDeflectionCoverage = 1
-
float phiMax = M_PI
-
float phiMin = -M_PI
-
float rMax = 0
-
std::vector<float> zBinEdges
-
float zMax = 0
-
float zMin = 0
-
inline SpacePointGridConfig toInternalUnits() const
-
class SpacePointGridCreator
- #include <Acts/Seeding/SpacePointGrid.hpp>
Public Static Functions
-
template<typename external_spacepoint_t>
static std::unique_ptr<SpacePointGrid<external_spacepoint_t>> createGrid(const Acts::SpacePointGridConfig &_config, const Acts::SpacePointGridOptions &_options)
-
template<typename external_spacepoint_t>
-
struct SpacePointGridOptions
- #include <Acts/Seeding/SpacePointGrid.hpp>
Public Functions
-
inline SpacePointGridOptions toInternalUnits() const
Public Members
-
float bFieldInZ = 0
-
bool isInInternalUnits = false
-
inline SpacePointGridOptions toInternalUnits() const
-
struct SpacePointParameters
- #include <Acts/Utilities/SpacePointUtility.hpp>
Storage container for variables related to the calculation of space points.
Public Members
-
Vector3 firstBtmToTop
Vector pointing from bottom to top end of first SDE.
-
Vector3 firstBtmToTopXvtxToFirstMid2
Cross product between firstBtmToTop and vtxToFirstMid2.
-
double limit = 1.
Regular limit of the absolute values of SpacePointParameters::m and SpacePointParameters::n.
-
double limitExtended = 0.
Limit of SpacePointParameters::m and SpacePointParameters::n in case of variable vertex.
-
double m = 0.
Parameter that determines the hit position on the first SDE.
-
double mag_firstBtmToTop = 0.
Magnitude of SpacePointParameters::firstBtmToTop.
-
double n = 0.
Parameter that determines the hit position on the second SDE.
-
Vector3 secondBtmToTop
Vector pointing from bottom to top end of second SDE.
-
Vector3 secondBtmToTopXvtxToSecondMid2
Cross product between secondBtmToTop and vtxToSecondMid2.
-
Vector3 vtxToFirstMid2
Twice the vector pointing from vertex to to midpoint of first SDE.
-
Vector3 vtxToSecondMid2
Twice the vector pointing from vertex to to midpoint of second SDE.
-
Vector3 firstBtmToTop
-
class SpacePointUtility
- #include <Acts/Utilities/SpacePointUtility.hpp>
Public Functions
-
inline SpacePointUtility(SpacePointBuilderConfig cfg)
Constructor.
-
Result<double> calcPerpendicularProjection(const std::pair<Vector3, Vector3> &stripEnds1, const std::pair<Vector3, Vector3> &stripEnds2, SpacePointParameters &spParams) const
Calculates a space point without using the vertex.
Note
This is mostly to resolve space points from cosmic data
Note
The meaning of the parameter is explained in more detail in the function body
- Parameters
stripEnds1 – The ends of one strip
stripEnds2 – The ends of another strip
spParams – SpacePointParamaters for the SP
- Returns
parameter that indicates the location of the space point; returns
if it failed
-
Vector2 calcRhoZVars(const GeometryContext &gctx, const SourceLink &slinkFront, const SourceLink &slinkBack, const SourceLinkSurfaceAccessor &surfaceAccessor, const std::function<std::pair<const BoundVector, const BoundSquareMatrix>(SourceLink)> ¶mCovAccessor, const Vector3 &globalPos, const double theta) const
Calculate the rho and z covariance from the front and back SourceLink in the strip SP formation.
- Parameters
gctx – The current geometry context object, e.g. alignment
slinkFront – The SourceLink on the front layer
slinkBack – The SourceLink on the back layer
paramCovAccessor – function to extract local position and covariance from SourceLink
surfaceAccessor – function to extract surface from SourceLink
globalPos – global position
theta – The angle between the two strips
- Returns
(rho, z) components of the global covariance
-
Result<void> calculateStripSPPosition(const std::pair<Vector3, Vector3> &stripEnds1, const std::pair<Vector3, Vector3> &stripEnds2, const Vector3 &posVertex, SpacePointParameters &spParams, const double stripLengthTolerance) const
This function performs a straight forward calculation of a space point and returns whether it was successful or not.
- Parameters
stripEnds1 – [in] Top and bottom end of the first strip
stripEnds2 – [in] Top and bottom end of the second strip
posVertex – [in] Position of the vertex
spParams – [inout] Data container of the calculations
stripLengthTolerance – [in] Tolerance scaling factor on the strip detector element length
- Returns
Result whether the space point calculation was successful
-
Result<double> differenceOfMeasurementsChecked(const Vector3 &pos1, const Vector3 &pos2, const Vector3 &posVertex, const double maxDistance, const double maxAngleTheta2, const double maxAnglePhi2) const
Calculates (Delta theta)^2 + (Delta phi)^2 between two SourceLinks.
- Parameters
pos1 – [in] position of the first SourceLink
pos2 – [in] position the second SourceLink
posVertex – [in] Position of the vertex
maxDistance – [in] Maximum distance between two SourceLinks
maxAngleTheta2 – [in] Maximum squared theta angle between two SourceLinks
maxAnglePhi2 – [in] Maximum squared phi angle between two SourceLinks
- Returns
Result with the squared sum within configuration parameters.
-
std::pair<Vector3, Vector2> globalCoords(const GeometryContext &gctx, const SourceLink &slink, const SourceLinkSurfaceAccessor &surfaceAccessor, const BoundVector &par, const BoundSquareMatrix &cov) const
Getter method for the global coordinates of a SourceLink.
- Parameters
gctx – The current geometry context object, e.g. alignment
slink – SourceLink that holds the necessary information
surfaceAccessor – function to extract surface from SourceLink
par – local position
cov – local covariance
- Returns
vectors of the global coordinates and covariance of the SourceLink
-
Result<void> recoverSpacePoint(SpacePointParameters &spParams, double stripLengthGapTolerance) const
This function tests if a space point can be estimated by a more tolerant treatment of construction.
In fact, this function indirectly allows shifts of the vertex.
- Parameters
spParams – [in] container that stores geometric parameters and rules of the space point formation
stripLengthGapTolerance – [in] Tolerance scaling factor of the gap between strip detector elements
- Returns
indicator if the test was successful
-
Vector2 rhoZCovariance(const GeometryContext &gctx, const Surface &surface, const Vector3 &globalPos, const SquareMatrix2 &localCov) const
Get rho and z covariance from the local position and covariance.
- Parameters
gctx – The current geometry context object, e.g. alignment
surface – The surface associated
globalPos – The global position
localCov – The local covariance matrix
- Returns
(rho, z) components of the global covariance
-
inline SpacePointUtility(SpacePointBuilderConfig cfg)
-
template<typename ...extensions>
struct StepperExtensionList : private detail::Extendable<extensions...> - #include <Acts/Propagator/StepperExtensionList.hpp>
Container of extensions used in the stepper of the propagation.
This struct allows a broadcast of function calls for each element in the list. The broadcasts occur for a certain function at each step in a specific order. The first function is an evaluater if an extension is or how many extensions are applicable for an upcoming step. The next functions called are the evaluations of the k_1 - k_4 or the RKN4 integration. The last function call in a step is the finalize() method. This method is an overloaded function (optionally propagates the covariance). Each method has the possibility to break the evaluation of a given step if an extension reports that something went wrong (e.g. a particle lost too much momentum during the step)
- Template Parameters
extensions – Types of the extensions
Public Functions
This functions broadcasts the call of the method finalize().
It collects all extensions and arguments and passes them forward for evaluation and returns a boolean.
This functions broadcasts the call of the method finalize().
It collects all extensions and arguments and passes them forward for evaluation and returns a boolean.
This functions broadcasts the call for evaluating a generic k.
It collects all arguments and extensions, test their validity for the evaluation and passes them forward for evaluation and returns a boolean as indicator if the evaluation is valid.
This functions broadcasts the call for evaluating k1.
It collects all arguments and extensions, test their validity for the evaluation and passes them forward for evaluation and returns a boolean as indicator if the evaluation is valid.
This functions broadcasts the call for evaluating k2.
It collects all arguments and extensions and passes them forward for evaluation and returns a boolean as indicator if the evaluation is valid.
This functions broadcasts the call for evaluating k3.
It collects all arguments and extensions and passes them forward for evaluation and returns a boolean as indicator if the evaluation is valid.
This functions broadcasts the call for evaluating k4.
It collects all arguments and extensions and passes them forward for evaluation and returns a boolean as indicator if the evaluation is valid.
Evaluation function to set valid extensions for an upcoming integration step.
- Template Parameters
propagator_state_t – Type of the state of the propagator
stepper_t – Type of the stepper
navigtor_t – Type of the navigator
- Parameters
state – [in] State of the propagator
stepper – [in] Stepper of the propagation
navigator – [in] Navigator of the propagation
-
class StraightLineStepper
- #include <Acts/Propagator/StraightLineStepper.hpp>
straight line stepper based on Surface intersection
The straight line stepper is a simple navigation stepper to be used to navigate through the tracking geometry. It can be used for simple material mapping, navigation validation
Public Types
-
using BField = NullBField
-
using BoundState = std::tuple<BoundTrackParameters, Jacobian, double>
-
using Covariance = BoundSquareMatrix
-
using CurvilinearState = std::tuple<CurvilinearTrackParameters, Jacobian, double>
-
using Jacobian = BoundMatrix
-
using state_type = State
Always use the same propagation state type, independently of the initial track parameter type and of the target surface.
Public Functions
-
StraightLineStepper() = default
-
inline double absoluteMomentum(const State &state) const
Absolute momentum accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
Result<BoundState> boundState(State &state, const Surface &surface, bool transportCov = true, const FreeToBoundCorrection &freeToBoundCorrection = FreeToBoundCorrection(false)) const
Create and return the bound state at the current position.
It does not check if the transported state is at the surface, this needs to be guaranteed by the propagator
- Parameters
state – [in] State that will be presented as
BoundStatesurface – [in] The surface to which we bind the state
transportCov – [in] Flag steering covariance transport
freeToBoundCorrection – [in] Correction for non-linearity effect during transform from free to bound
- Returns
A bound state:
the parameters at the surface
the stepwise jacobian towards it (from last bound)
and the path length (from start - for ordering)
-
inline double charge(const State &state) const
Charge access.
- Parameters
state – [in] The stepping state (thread-local cache)
-
CurvilinearState curvilinearState(State &state, bool transportCov = true) const
Create and return a curvilinear state at the current position.
This creates a curvilinear state.
- Parameters
state – [in] State that will be presented as
CurvilinearStatetransportCov – [in] Flag steering covariance transport
- Returns
A curvilinear state:
the curvilinear parameters at given position
the stepweise jacobian towards it (from last bound)
and the path length (from start - for ordering)
-
inline Vector3 direction(const State &state) const
Momentum direction accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline Result<Vector3> getField(State &state, const Vector3 &pos) const
Get the field for the stepping, this gives back a zero field.
- Parameters
state – [inout] is the propagation state associated with the track the magnetic field cell is used (and potentially updated)
pos – [in] is the field position
-
inline double getStepSize(const State &state, ConstrainedStep::Type stype) const
Get the step size.
- Parameters
state – [in] The stepping state (thread-local cache)
stype – [in] The step size type to be returned
-
template<typename charge_t>
inline State makeState(std::reference_wrapper<const GeometryContext> gctx, std::reference_wrapper<const MagneticFieldContext> mctx, const GenericBoundTrackParameters<charge_t> &par, double ssize = std::numeric_limits<double>::max(), double stolerance = s_onSurfaceTolerance) const
-
inline Vector3 momentum(const State &state) const
Momentum accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline std::string outputStepSize(const State &state) const
Output the Step Size - single component.
- Parameters
state – [in,out] The stepping state (thread-local cache)
-
inline double overstepLimit(const State &state) const
Overstep limit.
- Parameters
state – The stepping state (thread-local cache)
-
inline Vector3 position(const State &state) const
Global particle position accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline double qOverP(const State &state) const
QoP direction accessor.
- Parameters
state – [in] The stepping state (thread-local cache)
-
inline void releaseStepSize(State &state) const
Release the Step size.
- Parameters
state – [in,out] The stepping state (thread-local cache)
-
void resetState(State &state, const BoundVector &boundParams, const BoundSquareMatrix &cov, const Surface &surface, const double stepSize = std::numeric_limits<double>::max()) const
Resets the state.
- Parameters
state – [inout] State of the stepper
boundParams – [in] Parameters in bound parametrisation
cov – [in] Covariance matrix
surface – [in] The reset
Statewill be on this surfacestepSize – [in] Step size
-
inline void setStepSize(State &state, double stepSize, ConstrainedStep::Type stype = ConstrainedStep::actor, bool release = true) const
Set Step size - explicitly with a double.
- Parameters
state – [in,out] The stepping state (thread-local cache)
stepSize – [in] The step size value
stype – [in] The step size type to be set
release – [in] Do we release the step size?
Perform a straight line propagation step.
- Parameters
state – [inout] is the propagation state associated with the track parameters that are being propagated. The state contains the desired step size, it can be negative during backwards track propagation, and since we’re using an adaptive algorithm, it can be modified by the stepper class during propagation.
- Returns
the step size taken
-
inline double time(const State &state) const
Time access.
- Parameters
state – [in] The stepping state (thread-local cache)
-
void transportCovarianceToBound(State &state, const Surface &surface, const FreeToBoundCorrection &freeToBoundCorrection = FreeToBoundCorrection(false)) const
Method for on-demand transport of the covariance to a new curvilinear frame at current position, or direction of the state - for the moment a dummy method.
Note
no check is done if the position is actually on the surface
- Template Parameters
surface_t – the surface type - ignored here
- Parameters
state – [inout] The stepper state
surface – [in] is the surface to which the covariance is forwarded to
freeToBoundCorrection – [in] Correction for non-linearity effect during transform from free to bound
-
void transportCovarianceToCurvilinear(State &state) const
Method for on-demand transport of the covariance to a new curvilinear frame at current position, or direction of the state - for the moment a dummy method.
- Parameters
state – [inout] State of the stepper
-
void update(State &state, const FreeVector &freeParams, const BoundVector &boundParams, const Covariance &covariance, const Surface &surface) const
Method to update a stepper state to the some parameters.
- Parameters
state – [inout] State object that will be updated
freeParams – [in] Free parameters that will be written into
stateboundParams – [in] Corresponding bound parameters used to update jacToGlobal in
statecovariance – [in] Covariance that will be written into
statesurface – [in] The surface used to update the jacToGlobal
-
void update(State &state, const Vector3 &uposition, const Vector3 &udirection, double qop, double time) const
Method to update the stepper state.
- Parameters
state – [inout] State object that will be updated
uposition – [in] the updated position
udirection – [in] the updated direction
qop – [in] the updated qop value
time – [in] the updated time value
-
template<typename object_intersection_t>
inline void updateStepSize(State &state, const object_intersection_t &oIntersection, bool release = true) const Update step size.
It checks the status to the reference surface & updates the step size accordingly
- Parameters
state – [in,out] The stepping state (thread-local cache)
oIntersection – [in] The ObjectIntersection to layer, boundary, etc
release – [in] boolean to trigger step size release
-
inline Intersection3D::Status updateSurfaceStatus(State &state, const Surface &surface, Direction navDir, const BoundaryCheck &bcheck, ActsScalar surfaceTolerance = s_onSurfaceTolerance, const Logger &logger = getDummyLogger()) const
Update surface status.
This method intersects the provided surface and update the navigation step estimation accordingly (hence it changes the state). It also returns the status of the intersection to trigger onSurface in case the surface is reached.
- Parameters
state – [inout] The stepping state (thread-local cache)
surface – [in] The surface provided
navDir – [in] The navigation direction
bcheck – [in] The boundary check for this status update
surfaceTolerance – [in] Surface tolerance used for intersection
logger – [in] A logger instance
-
struct State
- #include <Acts/Propagator/StraightLineStepper.hpp>
State for track parameter propagation.
Public Functions
-
State() = delete
-
template<typename charge_t>
inline explicit State(const GeometryContext &gctx, const MagneticFieldContext &mctx, const GenericBoundTrackParameters<charge_t> &par, double ssize = std::numeric_limits<double>::max(), double stolerance = s_onSurfaceTolerance) Constructor from the initial bound track parameters.
Note
the covariance matrix is copied when needed
- Template Parameters
charge_t – Type of the bound parameter charge
- Parameters
gctx – [in] is the context object for the geometry
mctx – [in] is the context object for the magnetic field
par – [in] The track parameters at start
ssize – [in] is the maximum step size
stolerance – [in] is the stepping tolerance
Public Members
-
double absCharge = UnitConstants::e
The absolute charge as the free vector can be 1/p or q/p.
-
Covariance cov = Covariance::Zero()
-
bool covTransport = false
Boolean to indicate if you need covariance transport.
-
FreeVector derivative = FreeVector::Zero()
The propagation derivative.
-
std::reference_wrapper<const GeometryContext> geoContext
-
BoundToFreeMatrix jacToGlobal = BoundToFreeMatrix::Zero()
Jacobian from local to the global frame.
-
FreeMatrix jacTransport = FreeMatrix::Identity()
Pure transport jacobian part from runge kutta integration.
-
FreeVector pars = FreeVector::Zero()
Internal free vector parameters.
-
double pathAccumulated = 0.
accummulated path length state
-
double previousStepSize = 0.
-
ConstrainedStep stepSize
adaptive step size of the runge-kutta integration
-
double tolerance = s_onSurfaceTolerance
The tolerance for the stepping.
-
State() = delete
-
using BField = NullBField
-
class StrawSurface : public Acts::LineSurface
- #include <Acts/Surfaces/StrawSurface.hpp>
Class for a StrawSurface in the TrackingGeometry to describe dirft tube and straw like detectors.

Public Functions
-
StrawSurface() = delete
-
~StrawSurface() override = default
-
inline virtual std::string name() const final
Return properly formatted class name for screen output */.
-
StrawSurface &operator=(const StrawSurface &other)
Assignment operator.
- Parameters
other – is the source surface for copying
-
virtual Polyhedron polyhedronRepresentation(const GeometryContext &gctx, size_t lseg) const final
Return a Polyhedron for the surfaces.
Note
if lseg is set to 1 then only the straw is created
- Parameters
gctx – The current geometry context object, e.g. alignment
lseg – Number of segments along curved lines, it represents the full 2*M_PI coverange, if lseg is set to 1 only the extrema are given
- Returns
A list of vertices and a face/facett description of it
-
inline virtual SurfaceType type() const final
Return the surface type.
-
StrawSurface() = delete
-
struct StripPairOptions
- #include <Acts/SpacePointFormation/SpacePointBuilderOptions.hpp>
Public Members
-
double diffDist = 100. * UnitConstants::mm
Accepted distance between two clusters.
-
double diffPhi2 = 1.
Accepted squared difference in phi for two clusters.
-
double diffTheta2 = 1.
Accepted squared difference in theta for two clusters.
- std::function< std::pair< const BoundVector, const BoundSquareMatrix > const SourceLink &)> paramCovAccessor
-
Vector3 vertex = {0., 0., 0.}
vertex position
-
double diffDist = 100. * UnitConstants::mm
-
class Surface : public virtual Acts::GeometryObject, public std::enable_shared_from_this<Surface>
- #include <Acts/Surfaces/Surface.hpp>
Abstract Base Class for tracking surfaces.
The Surface class builds the core of the Acts Tracking Geometry. All other geometrical objects are either extending the surface or are built from it.
Surfaces are either owned by Detector elements or the Tracking Geometry, in which case they are not copied within the data model objects.
Subclassed by Acts::ConeSurface, Acts::CylinderSurface, Acts::DiscSurface, Acts::LineSurface, Acts::PlaneSurface
Public Types
-
enum SurfaceType
This enumerator simplifies the persistency & calculations, by saving a dynamic_cast, e.g.
for persistency
Values:
-
enumerator Cone
-
enumerator Cylinder
-
enumerator Disc
-
enumerator Perigee
-
enumerator Plane
-
enumerator Straw
-
enumerator Curvilinear
-
enumerator Other
-
enumerator Cone
Public Functions
-
virtual ~Surface()
-
AlignmentToBoundMatrix alignmentToBoundDerivative(const GeometryContext &gctx, const FreeVector ¶meters, const FreeVector &pathDerivative) const
The derivative of bound track parameters w.r.t.
alignment parameters of its reference surface (i.e. local frame origin in global 3D Cartesian coordinates and its rotation represented with extrinsic Euler angles)
- Parameters
gctx – The current geometry context object, e.g. alignment change of alignment parameters
parameters – is the free parameters
pathDerivative – is the derivative of free parameters w.r.t. path length
- Returns
Derivative of bound track parameters w.r.t. local frame alignment parameters
-
virtual AlignmentToPathMatrix alignmentToPathDerivative(const GeometryContext &gctx, const FreeVector ¶meters) const
Calculate the derivative of path length at the geometry constraint or point-of-closest-approach w.r.t.
alignment parameters of the surface (i.e. local frame origin in global 3D Cartesian coordinates and its rotation represented with extrinsic Euler angles)
Note
Re-implementation is needed for surface whose intersection with track is not its local xy plane, e.g. LineSurface, CylinderSurface and ConeSurface
- Parameters
gctx – The current geometry context object, e.g. alignment
parameters – is the free parameters
- Returns
Derivative of path length w.r.t. the alignment parameters
-
void assignDetectorElement(const DetectorElementBase &detelement)
Assign a detector element.
- Parameters
detelement – Detector element which is represented by this surface
Assign the surface material description.
The material is usually derived in a complicated way and loaded from a framework given source. As various surfaces may share the same source this is provided by a shared pointer
- Parameters
material – Material description associated to this surface
-
const DetectorElementBase *associatedDetectorElement() const
Return method for the associated Detector Element.
- Returns
plain pointer to the DetectorElement, can be nullptr
-
const Layer *associatedLayer() const
Return method for the associated Layer in which the surface is embedded.
- Returns
Layer by plain pointer, can be nullptr
-
void associateLayer(const Layer &lay)
Set Associated Layer Many surfaces can be associated to a Layer, but it might not be known yet during construction of the layer, this can be set afterwards.
- Parameters
lay – the assignment Layer by reference
-
virtual const SurfaceBounds &bounds() const = 0
Return method for SurfaceBounds.
- Returns
SurfaceBounds by reference
-
virtual BoundToFreeMatrix boundToFreeJacobian(const GeometryContext &gctx, const BoundVector &boundParams) const
Calculate the jacobian from local to global which the surface knows best, hence the calculation is done here.
Note
In principle, the input could also be a free parameters vector as it could be transformed to a bound parameters. But the transform might fail in case the parameters is not on surface. To avoid the check inside this function, it takes directly the bound parameters as input (then the check might be done where this function is called).
- Parameters
gctx – The current geometry context object, e.g. alignment
boundParams – is the bound parameters vector
- Returns
Jacobian from local to global
-
virtual Vector3 center(const GeometryContext &gctx) const
Return method for the surface center by reference.
Note
the center is always recalculated in order to not keep a cache
- Parameters
gctx – The current geometry context object, e.g. alignment
- Returns
center position by value
-
virtual FreeToBoundMatrix freeToBoundJacobian(const GeometryContext &gctx, const FreeVector ¶meters) const
Calculate the jacobian from global to local which the surface knows best, hence the calculation is done here.
Note
It assumes the input free parameters is on surface, hence no onSurface check is done inside this function.
- Parameters
gctx – The current geometry context object, e.g. alignment
parameters – is the free parameters
- Returns
Jacobian from global to local
-
virtual FreeToPathMatrix freeToPathDerivative(const GeometryContext &gctx, const FreeVector ¶meters) const
Calculate the derivative of path length at the geometry constraint or point-of-closest-approach w.r.t.
free parameters. The calculation is identical for all surfaces where the reference frame does not depend on the direction
- Parameters
gctx – The current geometry context object, e.g. alignment
parameters – is the free parameters
- Returns
Derivative of path length w.r.t. free parameters
Retrieve a
std::shared_ptrfor this surface (non-const version)Note
Will error if this was not created through the
makeSharedfactory since it needs access to the original reference. In C++14 this is undefined behavior (but most likely implemented as abad_weak_ptrexception), in C++17 it is defined as that exception.Note
Only call this if you need shared ownership of this object.
- Returns
The shared pointer
Retrieve a
std::shared_ptrfor this surface (const version)Note
Will error if this was not created through the
makeSharedfactory since it needs access to the original reference. In C++14 this is undefined behavior, but most likely implemented as abad_weak_ptrexception, in C++17 it is defined as that exception.Note
Only call this if you need shared ownership of this object.
- Returns
The shared pointer
-
virtual Result<Vector2> globalToLocal(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, double tolerance = s_onSurfaceTolerance) const = 0
Global to local transformation Generalized global to local transformation for the surface types.
Since some surface types need the global momentum/direction to resolve sign ambiguity this is also provided
- Parameters
gctx – The current geometry context object, e.g. alignment
position – global 3D position - considered to be on surface but not inside bounds (check is done)
direction – global 3D momentum direction
tolerance – optional tolerance within which a point is considered valid on surface
- Returns
a Result<Vector2> which can be !ok() if the operation fails
-
virtual bool insideBounds(const Vector2 &lposition, const BoundaryCheck &bcheck = true) const
The insideBounds method for local positions.
- Parameters
lposition – The local position to check
bcheck – BoundaryCheck directive for this onSurface check
- Returns
boolean indication if operation was successful
-
virtual SurfaceIntersection intersect(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck = false, ActsScalar tolerance = s_onSurfaceTolerance) const = 0
Straight line intersection schema from position/direction.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The position to start from
direction – The direction at start
bcheck – the Boundary Check
tolerance – the tolerance used for the intersection
- Returns
SurfaceIntersection object (contains intersection & surface)
-
bool isOnSurface(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction, const BoundaryCheck &bcheck = true) const
The geometric onSurface method.
Geometrical check whether position is on Surface
- Parameters
gctx – The current geometry context object, e.g. alignment
position – global position to be evaludated
direction – global momentum direction (required for line-type surfaces)
bcheck – BoundaryCheck directive for this onSurface check
- Returns
boolean indication if operation was successful
-
virtual ActsMatrix<2, 3> localCartesianToBoundLocalDerivative(const GeometryContext &gctx, const Vector3 &position) const = 0
Calculate the derivative of bound track parameters local position w.r.t.
position in local 3D Cartesian coordinates
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The position of the parameters in global
- Returns
Derivative of bound local position w.r.t. position in local 3D cartesian coordinates
-
virtual Vector3 localToGlobal(const GeometryContext &gctx, const Vector2 &lposition, const Vector3 &direction) const = 0
Local to global transformation Generalized local to global transformation for the surface types.
Since some surface types need the global momentum/direction to resolve sign ambiguity this is also provided
- Parameters
gctx – The current geometry context object, e.g. alignment
lposition – local 2D position in specialized surface frame
direction – global 3D momentum direction
- Returns
The global position by value
-
virtual std::string name() const = 0
Return properly formatted class name.
-
inline virtual Vector3 normal(const GeometryContext &gctx) const
Return method for the normal vector of the surface.
It will return a normal vector at the center() position
- Parameters
gctx – The current geometry context object, e.g. alignment
- Returns
normal vector by value
-
virtual Vector3 normal(const GeometryContext &gctx, const Vector2 &lposition) const = 0
Return method for the normal vector of the surface The normal vector can only be generally defined at a given local position It requires a local position to be given (in general)
- Parameters
gctx – The current geometry context object, e.g. alignment
lposition – is the local position where the normal vector is constructed
- Returns
normal vector by value
-
virtual Vector3 normal(const GeometryContext &gctx, const Vector3 &position) const
Return method for the normal vector of the surface The normal vector can only be generally defined at a given local position It requires a local position to be given (in general)
- Parameters
position – is the global position where the normal vector is constructed
gctx – The current geometry context object, e.g. alignment
- Returns
normal vector by value
-
virtual bool operator!=(const Surface &sf) const
Comparison (non-equality) operator.
- Parameters
sf – Source surface for the comparison
-
Surface &operator=(const Surface &other)
Assignment operator.
Note
copy construction invalidates the association to detector element and layer
- Parameters
other – Source surface for the assignment
-
virtual bool operator==(const Surface &other) const
Comparison (equality) operator The strategy for comparison is (a) first pointer comparison (b) then type comparison (c) then bounds comparison (d) then transform comparison.
- Parameters
other – source surface for the comparison
-
virtual double pathCorrection(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const = 0
Calucation of the path correction for incident.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – global 3D position - considered to be on surface but not inside bounds (check is done)
direction – global 3D momentum direction
- Returns
Path correction with respect to the nominal incident.
-
virtual Polyhedron polyhedronRepresentation(const GeometryContext &gctx, size_t lseg) const = 0
Return a Polyhedron for this object.
Note
An internal surface transform can invalidate the extrema in the transformed space
- Parameters
gctx – The current geometry context object, e.g. alignment
lseg – Number of segments along curved lines, if the lseg is set to one, only the corners and the extrema are given, otherwise it represents the number of segments for a full 2*M_PI circle and is scaled to the relevant sector
- Returns
A list of vertices and a face/facett description of it
-
virtual Acts::RotationMatrix3 referenceFrame(const GeometryContext &gctx, const Vector3 &position, const Vector3 &direction) const
Return method for the reference frame This is the frame in which the covariance matrix is defined (specialized by all surfaces)
- Parameters
gctx – The current geometry context object, e.g. alignment
position – global 3D position - considered to be on surface but not inside bounds (check is done)
direction – global 3D momentum direction (optionally ignored)
- Returns
RotationMatrix3 which defines the three axes of the measurement frame
-
const ISurfaceMaterial *surfaceMaterial() const
Return method for the associated Material to this surface.
- Returns
SurfaceMaterial as plain pointer, can be nullptr
Return method for the shared pointer to the associated Material.
- Returns
SurfaceMaterial as shared_pointer, can be nullptr
-
virtual std::ostream &toStream(const GeometryContext &gctx, std::ostream &sl) const
Output Method for std::ostream, to be overloaded by child classes.
- Parameters
gctx – The current geometry context object, e.g. alignment
sl – is the ostream to be dumped into
-
std::string toString(const GeometryContext &gctx) const
Output into a std::string.
- Parameters
gctx – The current geometry context object, e.g. alignment
-
virtual const Transform3 &transform(const GeometryContext &gctx) const
Return method for the surface Transform3 by reference In case a detector element is associated the surface transform is just forwarded to the detector element in order to keep the (mis-)alignment cache cetrally handled.
- Parameters
gctx – The current geometry context object, e.g. alignment
- Returns
the contextual transform
-
virtual SurfaceType type() const = 0
Return method for the Surface type to avoid dynamic casts.
Public Static Functions
Factory for producing memory managed instances of Surface.
Will forward all parameters and will attempt to find a suitable constructor.
Public Static Attributes
-
static std::array<std::string, SurfaceType::Other> s_surfaceTypeNames
Helper strings for screen output.
-
enum SurfaceType
-
class SurfaceArray
- #include <Acts/Surfaces/SurfaceArray.hpp>
Provides Surface binning in N dimensions.
Uses
Gridunder the hood to implement the storage and lookup Contains a lookup struct which talks to theGridand performs utility actions. This struct needs to be initialised externally and passed toSurfaceArrayon construction.Public Functions
Constructor with a single surface.
- Parameters
srf – The one and only surface
Default constructor which takes a
SurfaceLookupand a vector of surfaces.- Parameters
gridLookup – The grid storage.
SurfaceArraydoes not fill it on its ownsurfaces – The input vector of surfaces. This is only for bookkeeping, so we can ask
transform – Optional additional transform for this SurfaceArray
-
inline SurfaceVector &at(const Vector3 &position)
Get all surfaces in bin given by position.
- Parameters
position – the lookup position
- Returns
reference to
SurfaceVectorcontained in bin at that position
-
inline const SurfaceVector &at(const Vector3 &position) const
Get all surfaces in bin given by position
pos.- Parameters
position – the lookup position
- Returns
const reference to
SurfaceVectorcontained in bin at that position
-
inline SurfaceVector &at(size_t bin)
Get all surfaces in bin given by global bin index
bin.- Parameters
bin – the global bin index
- Returns
reference to
SurfaceVectorcontained in bin
-
inline const SurfaceVector &at(size_t bin) const
Get all surfaces in bin given by global bin index.
- Parameters
bin – the global bin index
- Returns
const reference to
SurfaceVectorcontained in bin
-
inline std::vector<BinningValue> binningValues() const
The binning values described by this surface grid lookup They are in order of the axes.
-
inline std::vector<const IAxis*> getAxes() const
Get vector of axes spanning the grid as
AnyAxis.Note
The axes in the vector are copies. Only use for introspection and querying.
- Returns
vector of
AnyAxis
-
inline Vector3 getBinCenter(size_t bin)
Get the center of the bin identified by global bin index
bin.- Parameters
bin – the global bin index
- Returns
Center position of the bin in global coordinates
-
inline bool isValidBin(size_t bin) const
Checks if global bin is valid.
Note
Valid means that the index points to a bin which is not a under or overflow bin or out of range in any axis.
- Parameters
bin – the global bin index
- Returns
bool if the bin is valid
-
inline const SurfaceVector &neighbors(const Vector3 &position) const
Get all surfaces in bin at
posand its neighbors.Note
The
SurfaceVectorwill be combined. For technical reasons, the different bin content vectors have to be copied, so the resulting vector contains copies.- Parameters
position – The position to lookup as nominal
- Returns
Merged
SurfaceVectorof neighbors and nominal
-
inline size_t size() const
Get the size of the underlying grid structure including under/overflow bins.
- Returns
the size
-
inline const SurfaceVector &surfaces() const
Get all surfaces attached to this
SurfaceArray.Note
This does not reflect the actual state of the grid. It only returns what was given in the constructor, without any checks if that is actually what’s in the grid.
- Returns
Reference to
SurfaceVectorcontaining all surfaces
-
std::ostream &toStream(const GeometryContext &gctx, std::ostream &sl) const
String representation of this
SurfaceArray.- Parameters
gctx – The current geometry context object, e.g. alignment
sl – Output stream to write to
- Returns
the output stream given as
sl
-
inline const Transform3 &transform() const
-
struct ISurfaceGridLookup
- #include <Acts/Surfaces/SurfaceArray.hpp>
Base interface for all surface lookups.
Subclassed by Acts::SurfaceArray::SingleElementLookup, Acts::SurfaceArray::SurfaceGridLookup< Axes >
Public Functions
-
virtual ~ISurfaceGridLookup() = 0
Pure virtual destructor.
-
inline virtual std::vector<BinningValue> binningValues() const
The binning values described by this surface grid lookup They are in order of the axes (optional) and empty for eingle lookups.
-
virtual size_t completeBinning(const GeometryContext &gctx, const SurfaceVector &surfaces) = 0
Attempts to fix sub-optimal binning by filling closest Surfaces into empty bin.
- Parameters
gctx – The current geometry context object, e.g. alignment
surfaces – The surface pointers to fill
- Returns
number of bins that were filled
-
virtual size_t dimensions() const = 0
Get the number of dimensions of the grid.
- Returns
number of dimensions
-
virtual void fill(const GeometryContext &gctx, const SurfaceVector &surfaces) = 0
Fill provided surfaces into the contained
Grid.- Parameters
gctx – The current geometry context object, e.g. alignment
surfaces – Input surface pointers
-
virtual std::vector<const IAxis*> getAxes() const = 0
Returns copies of the axes used in the grid as
AnyAxis.Note
This returns copies. Use for introspection and querying.
- Returns
The axes
-
virtual Vector3 getBinCenter(size_t bin) const = 0
Gets the center position of bin
binin global coordinates.- Parameters
bin – the global bin index
- Returns
The bin center
-
virtual bool isValidBin(size_t bin) const = 0
Checks if global bin is valid.
Note
Valid means that the index points to a bin which is not a under or overflow bin or out of range in any axis.
- Parameters
bin – the global bin index
- Returns
bool if the bin is valid
-
virtual const SurfaceVector &lookup(const Vector3 &position) const = 0
Performs lookup at
posand returns bin content as const reference.- Parameters
position – Lookup position
- Returns
SurfaceVectorat given bin
-
virtual SurfaceVector &lookup(const Vector3 &position) = 0
Performs lookup at
posand returns bin content as reference.- Parameters
position – Lookup position
- Returns
SurfaceVectorat given bin
-
virtual const SurfaceVector &lookup(size_t bin) const = 0
Performs lookup at global bin and returns bin content as const reference.
- Parameters
bin – Global lookup bin
- Returns
SurfaceVectorat given bin
-
virtual SurfaceVector &lookup(size_t bin) = 0
Performs lookup at global bin and returns bin content as reference.
- Parameters
bin – Global lookup bin
- Returns
SurfaceVectorat given bin
-
virtual const SurfaceVector &neighbors(const Vector3 &position) const = 0
Performs a lookup at
pos, but returns neighbors as well.- Parameters
position – Lookup position
- Returns
SurfaceVectorat given bin. Copy of all bins selected
-
virtual size_t size() const = 0
Returns the total size of the grid (including under/overflow bins)
- Returns
Size of the grid data structure
-
virtual ~ISurfaceGridLookup() = 0
-
struct SingleElementLookup : public Acts::SurfaceArray::ISurfaceGridLookup
- #include <Acts/Surfaces/SurfaceArray.hpp>
Lookup implementation which wraps one element and always returns this element when lookup is called.
Public Functions
-
inline SingleElementLookup(SurfaceVector::value_type element)
Default constructor.
- Parameters
element – the one and only element.
-
inline virtual size_t completeBinning(const GeometryContext&, const SurfaceVector&) override
Comply with concept and provide completeBinning method.
Note
Does nothing
-
inline virtual size_t dimensions() const override
Get the number of dimensions.
- Returns
always 0
-
inline virtual void fill(const GeometryContext&, const SurfaceVector&) override
Comply with concept and provide fill method.
Note
Does nothing
-
inline virtual std::vector<const IAxis*> getAxes() const override
Returns an empty vector of
AnyAxis.- Returns
empty vector
-
inline virtual Vector3 getBinCenter(size_t bin) const override
Gets the bin center, but always returns (0, 0, 0)
- Parameters
bin – is ignored
- Returns
(0, 0, 0)
-
inline virtual bool isValidBin(size_t bin) const override
Returns if the bin is valid (it is)
- Parameters
bin – is ignored
- Returns
always true
-
inline virtual const SurfaceVector &lookup(const Vector3 &position) const override
Lookup, always returns
element.- Parameters
position – is ignored
- Returns
reference to vector containing only
element
-
inline virtual SurfaceVector &lookup(const Vector3 &position) override
Lookup, always returns
element.- Parameters
position – is ignored
- Returns
reference to vector containing only
element
-
inline virtual const SurfaceVector &lookup(size_t bin) const override
Lookup, always returns
element.- Parameters
bin – is ignored
- Returns
reference to vector containing only
element
-
inline virtual SurfaceVector &lookup(size_t bin) override
Lookup, always returns
element.- Parameters
bin – is ignored
- Returns
reference to vector containing only
element
-
inline virtual const SurfaceVector &neighbors(const Vector3 &position) const override
Lookup, always returns
element.- Parameters
position – is ignored
- Returns
reference to vector containing only
element
-
inline virtual size_t size() const override
returns 1
- Returns
1
-
inline SingleElementLookup(SurfaceVector::value_type element)
-
template<class ...Axes>
struct SurfaceGridLookup : public Acts::SurfaceArray::ISurfaceGridLookup - #include <Acts/Surfaces/SurfaceArray.hpp>
Lookup helper which encapsulates a
Grid.- Template Parameters
Axes – The axes used for the grid
Public Types
-
using Grid_t = detail::Grid<SurfaceVector, Axes...>
-
using point_t = std::conditional_t<DIM == 1, std::array<double, 1>, ActsVector<DIM>>
Specifies the local coordinate type.
This resolves to
ActsVector<DIM>for DIM > 1, elsestd::array<double, 1>
Public Functions
-
inline SurfaceGridLookup(std::function<point_t(const Vector3&)> globalToLocal, std::function<Vector3(const point_t&)> localToGlobal, std::tuple<Axes...> axes, std::vector<BinningValue> bValues = {})
Default constructor.
Note
Signature of localToGlobal and globalToLocal depends on
DIM. If DIM > 1, local coords areActsVector<DIM>elsestd::array<double, 1>.- Parameters
globalToLocal – Callable that converts from global to local
localToGlobal – Callable that converts from local to global
axes – The axes to build the grid data structure.
bValues – What the axes represent (optional)
-
inline virtual std::vector<BinningValue> binningValues() const override
The binning values described by this surface grid lookup They are in order of the axes.
-
inline virtual size_t completeBinning(const GeometryContext &gctx, const SurfaceVector &surfaces) override
Attempts to fix sub-optimal binning by filling closest Surfaces into empty bins.
Note
This does not always do what you want.
- Parameters
gctx – The current geometry context object, e.g. alignment
surfaces – The surface pointers to fill
- Returns
number of bins that were filled
-
inline virtual size_t dimensions() const override
Get the number of dimensions of the grid.
- Returns
number of dimensions
-
inline virtual void fill(const GeometryContext &gctx, const SurfaceVector &surfaces) override
Fill provided surfaces into the contained
Grid.This is done by iterating, accessing the binningPosition, lookup and append. Also populates the neighbor map by combining the filled bins of all bins around a given one.
- Parameters
gctx – The current geometry context object, e.g. alignment
surfaces – Input surface pointers
-
inline virtual std::vector<const IAxis*> getAxes() const override
Returns copies of the axes used in the grid as
AnyAxis.Note
This returns copies. Use for introspection and querying.
- Returns
The axes
-
inline virtual Vector3 getBinCenter(size_t bin) const override
Gets the center position of bin
binin global coordinates.- Parameters
bin – the global bin index
- Returns
The bin center
-
inline virtual bool isValidBin(size_t bin) const override
Checks if global bin is valid.
Note
Valid means that the index points to a bin which is not a under or overflow bin or out of range in any axis.
- Parameters
bin – the global bin index
- Returns
bool if the bin is valid
-
inline virtual const SurfaceVector &lookup(const Vector3 &position) const override
Performs lookup at
posand returns bin content as const reference.- Parameters
position – Lookup position
- Returns
SurfaceVectorat given bin
-
inline virtual SurfaceVector &lookup(const Vector3 &position) override
Performs lookup at
posand returns bin content as reference.- Parameters
position – Lookup position
- Returns
SurfaceVectorat given bin
-
inline virtual const SurfaceVector &lookup(size_t bin) const override
Performs lookup at global bin and returns bin content as const reference.
- Parameters
bin – Global lookup bin
- Returns
SurfaceVectorat given bin
-
inline virtual SurfaceVector &lookup(size_t bin) override
Performs lookup at global bin and returns bin content as reference.
- Parameters
bin – Global lookup bin
- Returns
SurfaceVectorat given bin
-
inline virtual const SurfaceVector &neighbors(const Vector3 &position) const override
Performs a lookup at
pos, but returns neighbors as well.- Parameters
position – Lookup position
- Returns
SurfaceVectorat given bin. Copy of all bins selected
-
inline virtual size_t size() const override
Returns the total size of the grid (including under/overflow bins)
- Returns
Size of the grid data structure
Public Static Attributes
-
static constexpr size_t DIM = sizeof...(Axes)
-
class SurfaceArrayCreator
- #include <Acts/Geometry/SurfaceArrayCreator.hpp>
It is designed create sub surface arrays to be ordered on Surfaces.
Public Functions
-
inline SurfaceArrayCreator(const Config &cfg, std::unique_ptr<const Logger> logger = getDefaultLogger("SurfaceArrayCreator", Logging::INFO))
Constructor with explicit config.
- Parameters
cfg – Explicit config struct
logger – logging instance
-
inline SurfaceArrayCreator(std::unique_ptr<const Logger> logger = getDefaultLogger("SurfaceArrayCreator", Logging::INFO))
Constructor with default config.
- Parameters
logger – logging instance
-
virtual ~SurfaceArrayCreator() = default
Destructor.
-
inline void setLogger(std::unique_ptr<const Logger> logger)
Set logging instance.
- Parameters
logger – is the logging instance to be set
SurfaceArrayCreator interface method.
create an array in a cylinder, binned in phi, z when extremas and bin numbers are unknown - this method goes through the surfaces and finds out the needed information
Warning
This function requires the cylinder aligned with the z-axis
- Parameters
surfaces – is the vector of pointers to sensitive surfaces to be ordered on the cylinder
gctx – [in] The gometry context for this building call
protoLayerOpt – The proto layer containing the layer size
bTypePhi – the binning type in phi direction (equidistant/arbitrary)
bTypeZ – the binning type in z direction (equidistant/arbitrary)
transform – is the (optional) additional transform applied
- Pre
the pointers to the sensitive surfaces in the surfaces vectors all need to be valid, since no check is performed
- Returns
a unique pointer a new SurfaceArray
SurfaceArrayCreator interface method.
create an array in a cylinder, binned in phi, z when extremas and bin numbers are known
Warning
This function requires the cylinder aligned with the z-axis
- Parameters
surfaces – is the vector of pointers to sensitive surfaces to be ordered on the cylinder
gctx – [in] The gometry context for this building call
protoLayerOpt – The proto layer containing the layer size
binsPhi – is the number of bins in phi for the surfaces
binsZ – is the number of bin in Z for the surfaces
transform – is the (optional) additional transform applied
- Pre
the pointers to the sensitive surfaces in the surfaces vectors all need to be valid, since no check is performed
- Returns
a unique pointer to a new SurfaceArray
SurfaceArrayCreator interface method.
create an array in a cylinder, binned in phi, r when extremas and bin numbers are unknown - this method goes through the surfaces and finds out the needed information
Note
If there is more than on R-Ring, number of phi bins will be set to lowest number of surfaces of any R-ring. This ignores bTypePhi and produces equidistant binning in phi
Warning
This function requires the disc aligned with the z-axis
- Parameters
surfaces – is the vector of pointers to sensitive surfaces to be ordered on the disc
gctx – [in] The gometry context for this building call
protoLayerOpt – The proto layer containing the layer size
bTypeR – the binning type in r direction (equidistant/arbitrary)
bTypePhi – the binning type in phi direction (equidistant/arbitrary)
transform – is the (optional) additional transform applied
- Pre
the pointers to the sensitive surfaces in the surfaces vectors all need to be valid, since no check is performed
- Returns
a unique pointer a new SurfaceArray
SurfaceArrayCreator interface method.
create an array on a disc, binned in r, phi when extremas and bin numbers are known
Warning
This function requires the disc aligned with the z-axis
- Parameters
surfaces – is the vector of pointers to sensitive surfaces to be ordered on the disc
gctx – [in] The gometry context for this building call
protoLayerOpt – The proto layer containing the layer size
binsPhi – is the number of bins in phi for the surfaces
binsR – is the number of bin in R for the surfaces
transform – is the (optional) additional transform applied
- Pre
the pointers to the sensitive surfaces in the surfaces vectors all need to be valid, since no check is performed
- Returns
a unique pointer a new SurfaceArray
SurfaceArrayCreator interface method.
create an array on a plane
Warning
This function requires the plane aligned with either the x-, y- or z-axis
- Parameters
gctx – [in] The gometry context for this building call
surfaces – [in] is the vector of pointers to sensitive surfaces to be ordered on the plane
bins1 – [in] is the number of bins in the orthogonal direction to
bValuebins2 – [in] is the number of bins in the orthogonal direction to
bValuebValue – [in] Direction of the aligned surfaces
protoLayerOpt – [in] Optional
ProtoLayerinstancetransform – [in] is the (optional) additional transform applied
- Pre
the pointers to the sensitive surfaces in the surfaces vectors all need to be valid, since no check is performed
- Returns
a unique pointer a new SurfaceArray
Public Static Functions
-
static inline bool isSurfaceEquivalent(const GeometryContext &gctx, BinningValue bValue, const Surface *a, const Surface *b)
Static check function for surface equivalent.
- Parameters
gctx – [in] the geometry context for this check
bValue – the binning value for the binning
a – first surface for checking
b – second surface for checking
Friends
- friend class Acts::SurfaceArray
- friend struct Acts::Test::SurfaceArrayCreatorFixture
-
struct Config
- #include <Acts/Geometry/SurfaceArrayCreator.hpp>
Public Members
-
bool doPhiBinningOptimization = true
Optimize the binning in phi for disc layers.
Reduces the number of bins to the lowest number of non-equivalent phi surfaces of all r-bins. If false, this step is skipped.
-
SurfaceMatcher surfaceMatcher = SurfaceArrayCreator::isSurfaceEquivalent
Type-erased function which determines whether two surfaces are supposed to be considered equivalent in terms of the binning.
-
bool doPhiBinningOptimization = true
-
struct ProtoAxis
- #include <Acts/Geometry/SurfaceArrayCreator.hpp>
Public Functions
-
inline size_t getBin(AxisScalar x) const
Public Members
-
std::vector<AxisScalar> binEdges
-
BinningType bType = BinningType::equidistant
-
BinningValue bValue = BinningValue::binX
-
AxisScalar max = 0
-
AxisScalar min = 0
-
size_t nBins = 0
-
inline size_t getBin(AxisScalar x) const
-
inline SurfaceArrayCreator(const Config &cfg, std::unique_ptr<const Logger> logger = getDefaultLogger("SurfaceArrayCreator", Logging::INFO))
-
struct SurfaceBinningMatcher
- #include <Acts/Geometry/SurfaceBinningMatcher.hpp>
Public Types
-
using Range = std::pair<double, double>
The binning tolerance parameters.
Public Functions
-
SurfaceBinningMatcher() = default
-
inline SurfaceBinningMatcher(const std::vector<Range> &tolpars)
-
inline bool operator()(const Acts::GeometryContext &gctx, Acts::BinningValue bValue, const Acts::Surface *one, const Acts::Surface *other) const
Check function for surface equivalent.
- Parameters
gctx – [in] gctx the geometry context for this check
bValue – the binning value for the binning
one – first surface for checking
other – second surface for checking
-
using Range = std::pair<double, double>
-
class SurfaceBounds
- #include <Acts/Surfaces/SurfaceBounds.hpp>
Interface for surface bounds.
Surface bounds provide:
inside() checks
distance to boundary calculations
the BoundsType and a set of parameters to simplify persistency
Subclassed by Acts::ConeBounds, Acts::CylinderBounds, Acts::DiscBounds, Acts::InfiniteBounds, Acts::LineBounds, Acts::PlanarBounds
Public Types
-
enum BoundsType
This is nested to the SurfaceBounds, as also VolumeBounds will have Bounds Type.
Values:
-
enumerator eCone
-
enumerator eCylinder
-
enumerator eDiamond
-
enumerator eDisc
-
enumerator eEllipse
-
enumerator eLine
-
enumerator eRectangle
-
enumerator eTrapezoid
-
enumerator eTriangle
-
enumerator eDiscTrapezoid
-
enumerator eConvexPolygon
-
enumerator eAnnulus
-
enumerator eBoundless
-
enumerator eOther
-
enumerator eCone
Public Functions
-
virtual ~SurfaceBounds() = default
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck) const = 0
Inside check for the bounds object driven by the boundary check directive Each Bounds has a method inside, which checks if a LocalPosition is inside the bounds Inside can be called without/with tolerances.
- Parameters
lposition – Local position (assumed to be in right surface frame)
bcheck – boundary check directive
- Returns
boolean indicator for the success of this operation
-
virtual std::ostream &toStream(std::ostream &os) const = 0
Output Method for std::ostream, to be overloaded by child classes.
- Parameters
os – is the outstream in which the string dump is done
-
virtual BoundsType type() const = 0
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
virtual std::vector<double> values() const = 0
Access method for bound values, this is a dynamically sized vector containing the parameters needed to describe these bounds.
- Returns
of the stored values for this SurfaceBounds object
-
template<typename Selector = SurfaceSelector>
struct SurfaceCollector - #include <Acts/Propagator/SurfaceCollector.hpp>
A Surface Collector struct templated with a Selector type.
Whenever a surface is passed in the propagation that satisfies the selector, it is recorded for further usage in the flow.
Public Types
-
using result_type = this_result
Public Functions
Collector action for the ActionList of the Propagator It checks if the propagator state has a current surface, in which case the action is performed:
it records the surface given the configuration
- Template Parameters
propagator_state_t – is the type of Propagator state
stepper_t – Type of the stepper used for the propagation
navigator_t – Type of the navigator used for the propagation
- Parameters
state – [inout] is the mutable stepper state object
stepper – [in] The stepper in use
navigator – [in] The navigator in use
result – [inout] is the mutable result object
logger – a logger instance
Public Members
-
Selector selector
The selector used for this surface.
-
struct this_result
- #include <Acts/Propagator/SurfaceCollector.hpp>
Simple result struct to be returned It has all the SurfaceHit objects that are collected (and thus have been selected)
Public Members
-
std::vector<SurfaceHit> collected
-
std::vector<SurfaceHit> collected
-
using result_type = this_result
-
struct SurfaceHit
- #include <Acts/Propagator/SurfaceCollector.hpp>
The information to be writtern out per hit surface.
-
class SurfaceMaterialMapper
- #include <Acts/Material/SurfaceMaterialMapper.hpp>
SurfaceMaterialMapper.
This is the main feature tool to map material information from a 3D geometry onto the TrackingGeometry with its surface material description.
The process runs as such:
1) TrackingGeometry is parsed and for each Surface with ProtoSurfaceMaterial a local store is initialized the identification is done hereby through the Surface::GeometryIdentifier
2) A Cache is generated that is used to keep the filling thread local, the filling is protected with std::mutex
3) A number of N material tracks is read in, each track has : origin, direction, material steps < position, step length, x0, l0, a, z, rho >
for each track: surfaces along the origin/direction path are collected the closest material steps are assigned
4) Each ‘hit’ bin per event is counted and averaged at the end of the run
Public Types
-
using StraightLinePropagator = Propagator<StraightLineStepper, Navigator>
Public Functions
-
SurfaceMaterialMapper() = delete
Delete the Default constructor.
-
SurfaceMaterialMapper(const Config &cfg, StraightLinePropagator propagator, std::unique_ptr<const Logger> slogger = getDefaultLogger("SurfaceMaterialMapper", Logging::INFO))
Constructor with config object.
- Parameters
cfg – Configuration struct
propagator – The straight line propagator
slogger – The logger
-
State createState(const GeometryContext &gctx, const MagneticFieldContext &mctx, const TrackingGeometry &tGeometry) const
helper method that creates the cache for the mapping
This method takes a TrackingGeometry, finds all surfaces with material proxis and returns you a Cache object tO be used
- Parameters
gctx – [in] The geometry context to use
mctx – [in] The magnetic field context to use
tGeometry – [in] The geometry which should be mapped
-
void finalizeMaps(State &mState) const
Method to finalize the maps.
It calls the final run averaging and then transforms the AccumulatedSurface material class to a surface material class type
- Parameters
mState –
-
void mapInteraction(State &mState, RecordedMaterialTrack &mTrack) const
Loop through all the material interactions and add them to the associated surface.
- Parameters
mState – The current state map
mTrack – The material track to be mapped
-
void mapMaterialTrack(State &mState, RecordedMaterialTrack &mTrack) const
Process/map a single track.
Note
the RecordedMaterialSlab of the track are assumed to be ordered from the starting position along the starting direction
- Parameters
mState – The current state map
mTrack – The material track to be mapped
-
void mapSurfaceInteraction(State &mState, std::vector<MaterialInteraction> &rMaterial) const
Loop through all the material interactions and add them to the associated surface.
Note
The material interactions are assumed to have an associated surface ID
- Parameters
mState – The current state map
rMaterial – Vector of all the material interactions that will be mapped
-
struct Config
- #include <Acts/Material/SurfaceMaterialMapper.hpp>
Nested Configuration struct for the material mapper.
Public Members
-
bool computeVariance = false
Compute the variance of each material slab (only if using an input map)
-
bool emptyBinCorrection = true
Correct for empty bins (recommended)
-
std::array<double, 2> etaRange = {{-6., 6.}}
Mapping range.
-
bool mapperDebugOutput = false
Mapping output to debug stream.
-
bool computeVariance = false
-
struct State
- #include <Acts/Material/SurfaceMaterialMapper.hpp>
Nested State struct which is used for the mapping prococess.
Public Functions
-
inline State(const GeometryContext &gctx, const MagneticFieldContext &mctx)
- Parameters
gctx – [in] The geometry context to use
mctx – [in] The magnetic field context to use
Public Members
-
std::map<GeometryIdentifier, AccumulatedSurfaceMaterial> accumulatedMaterial
The accumulated material per geometry ID.
-
std::reference_wrapper<const GeometryContext> geoContext
Reference to the geometry context for the mapping.
-
std::map<GeometryIdentifier, std::shared_ptr<const ISurfaceMaterial>> inputSurfaceMaterial
The surface material of the input tracking geometry.
-
std::reference_wrapper<const MagneticFieldContext> magFieldContext
Reference to the magnetic field context.
-
std::map<GeometryIdentifier, std::unique_ptr<const ISurfaceMaterial>> surfaceMaterial
The created surface material from it.
-
std::map<GeometryIdentifier, std::shared_ptr<const IVolumeMaterial>> volumeMaterial
The volume material of the input tracking geometry.
-
inline State(const GeometryContext &gctx, const MagneticFieldContext &mctx)
-
using StraightLinePropagator = Propagator<StraightLineStepper, Navigator>
-
struct SurfaceReached
- #include <Acts/Propagator/StandardAborters.hpp>
This is the condition that the Surface has been reached it then triggers an propagation abort of the propagation.
Public Functions
-
SurfaceReached() = default
boolean operator for abort condition without using the result
- Template Parameters
propagator_state_t – Type of the propagator state
stepper_t – Type of the stepper
navigator_t – Type of the navigator
- Parameters
state – [inout] The propagation state object
stepper – [in] Stepper used for propagation
navigator – [in] Navigator used for propagation
logger – a logger instance
boolean operator for abort condition without using the result
- Template Parameters
propagator_state_t – Type of the propagator state
stepper_t – Type of the stepper
navigator_t – Type of the navigator
- Parameters
state – [inout] The propagation state object
stepper – [in] Stepper used for the propagation
navigator – [in] Navigator used for the propagation
targetSurface – [in] The target surface
logger – a logger instance
-
SurfaceReached() = default
-
struct SurfaceSelector
- #include <Acts/Propagator/SurfaceCollector.hpp>
Simple struct to select surfaces.
Public Functions
-
inline SurfaceSelector(bool sSensitive = true, bool sMaterial = false, bool sPassive = false)
SurfaceSelector with options.
- Parameters
sSensitive – is the directive to select sensitive surfaces
sMaterial – is the directive to select material surfaces
sPassive – is the directive to select passive surfaces
Public Members
-
bool selectMaterial = false
-
bool selectPassive = false
-
bool selectSensitive = true
-
inline SurfaceSelector(bool sSensitive = true, bool sMaterial = false, bool sPassive = false)
-
struct TargetOptions
- #include <Acts/Propagator/StandardAborters.hpp>
TargetOptions struct for geometry interface.
Public Functions
-
inline TargetOptions(Direction ndir)
create target options
Public Members
-
BoundaryCheck boundaryCheck = false
Target Boundary check directive - always false here.
Navigation direction.
-
double pathLimit = std::numeric_limits<double>::max()
The path limit.
-
const Surface *startObject = nullptr
Object to check against - always nullptr here.
-
inline TargetOptions(Direction ndir)
-
class TGeoCylinderDiscSplitter : public Acts::ITGeoDetectorElementSplitter
- #include <Acts/Plugins/TGeo/TGeoCylinderDiscSplitter.hpp>
TGeoCylinderDiscSplitter.
Split Cylinder and disks into submodules
Public Functions
-
TGeoCylinderDiscSplitter(const Config &cfg, std::unique_ptr<const Acts::Logger> logger = Acts::getDefaultLogger("TGeoCylinderDiscSplitter", Acts::Logging::INFO))
Constructor.
- Parameters
cfg – the configuration struct
logger – the logging object
-
~TGeoCylinderDiscSplitter() override = default
Take a geometry context and TGeoElement and split it into sub elements.
Note
If no split is performed the unsplit detector element is returned
- Parameters
gctx – is a geometry context object
tgde – is a TGeoDetectorElement that is eventually split
- Returns
a vector of TGeoDetectorElement objects
-
struct Config
- #include <Acts/Plugins/TGeo/TGeoCylinderDiscSplitter.hpp>
Nested configuration struct.
Public Members
-
int cylinderLongitudinalSegments = -1
Number of segments in r for a disk.
-
int cylinderPhiSegments = -1
Number of segments in phi for a disc.
-
int discPhiSegments = -1
Number of segments in phi for a disc.
-
int discRadialSegments = -1
Number of segments in r for a disk.
-
int cylinderLongitudinalSegments = -1
-
TGeoCylinderDiscSplitter(const Config &cfg, std::unique_ptr<const Acts::Logger> logger = Acts::getDefaultLogger("TGeoCylinderDiscSplitter", Acts::Logging::INFO))
-
class TGeoDetectorElement : public Acts::IdentifiedDetectorElement
- #include <Acts/Plugins/TGeo/TGeoDetectorElement.hpp>
DetectorElement plugin for ROOT TGeo shapes.
Added possibility to hand over transformation matrix.
Subclassed by Acts::DD4hepDetectorElement
Public Types
-
using ContextType = GeometryContext
Broadcast the context type.
Public Functions
Constructor.
Note
this constructor used auto-translation
Note
This parameter only needs to be set for plane modules
Note
In the translation from a 3D geometry (TGeo) which only knows tubes to a 2D geometry (Tracking geometry) a distinction if the module should be described as a cylinder or a disc surface needs to be done. Since this information can not be taken just from the geometry description (both can be described as TGeoTubeSeg), one needs to set the flag ‘isDisc’ in case a volume with shape
TGeoTubeSegshould be translated to a disc surface. Per default it will be translated into a cylindrical surface.- Parameters
identifier – is the detector identifier
tGeoNode – is the TGeoNode which should be represented
tGeoMatrix – The Matrix to global (i.e. ACTS transform)
axes – is the axis orientation with respect to the tracking frame it is a string of the three characters x, y and z (standing for the three axes) there is a distinction between capital and lower case characters :
capital -> positive orientation of the axis
lower case -> negative orientation of the axis example options are “XYZ” -> identical frame definition (default value) “YZX” -> node y axis is tracking x axis, etc. “XzY” -> negative node z axis is tracking y axis, etc.
scalor – is the scale factor for unit conversion if needed
material – Possible material of detector element
Constructor with pre-computed disk surface.
Note
this detector element constructor needs everything pre-computed.
- Parameters
identifier – is the detector identifier
tGeoNode – is the TGeoNode which should be represented
tgTransform – the transform of this detector element
tgBounds – the bounds of this surface
tgThickness – the thickness of this detector element
Constructor with pre-computed surface.
Note
this detector element constructor needs everything pre-computed.
- Parameters
identifier – is the detector identifier
tGeoNode – is the TGeoNode which should be represented
tgTransform – the transform of this detector element
tgBounds – the bounds of this surface
tgThickness – the thickness of this detector element
-
~TGeoDetectorElement() override
-
inline virtual const std::shared_ptr<const DigitizationModule> digitizationModule() const final
Retrieve the DigitizationModule.
-
inline virtual Identifier identifier() const final
Retrieve the Identifier.
-
inline const Surface &surface() const override
Return surface associated with this detector element.
-
inline Surface &surface() override
Return surface associated with this detector element.
Note
this is the non-const access
-
inline const TGeoNode &tgeoNode() const
Return the TGeoNode for back navigation.
-
inline double thickness() const override
Returns the thickness of the module.
-
inline const Transform3 &transform(const GeometryContext &gctx) const override
Return local to global transform associated with this identifier.
- Parameters
gctx – The current geometry context object, e.g. alignment
-
using ContextType = GeometryContext
-
class TGeoLayerBuilder : public Acts::ILayerBuilder
- #include <Acts/Plugins/TGeo/TGeoLayerBuilder.hpp>
This parses the gGeoManager and looks for a defined combination of volume with contained sensitive detector element.
The association is done by matching the names of the TGeoNode / TGeoVolume to the search string.
The parsing can be restricted to a given parse volume (in r and z), and given some splitting parameters the surfaces can be automatically split into layers.
Public Types
-
using ElementFactory = std::function<std::shared_ptr<TGeoDetectorElement>(const Identifier&, const TGeoNode&, const TGeoMatrix &tGeoMatrix, const std::string &axes, double scalor, std::shared_ptr<const Acts::ISurfaceMaterial> material)>
Public Functions
-
TGeoLayerBuilder(const Config &config, std::unique_ptr<const Logger> logger = getDefaultLogger("TGeoLayerBuilder", Logging::INFO))
Constructor.
- Parameters
config – is the configuration struct
logger – the local logging instance
-
~TGeoLayerBuilder() override
Destructor.
-
virtual const LayerVector centralLayers(const GeometryContext &gctx) const final
LayerBuilder interface method - returning the central layers.
- Parameters
gctx – the geometry context for this build call
-
inline const std::vector<std::shared_ptr<const TGeoDetectorElement>> &detectorElements() const
Return the created detector elements.
-
inline Config getConfiguration() const
Get the configuration object.
-
inline virtual const std::string &identification() const final
Name identification.
-
virtual const LayerVector negativeLayers(const GeometryContext &gctx) const final
LayerBuilder interface method - returning the layers at negative side.
- Parameters
gctx – the geometry context for this build call
-
virtual const LayerVector positiveLayers(const GeometryContext &gctx) const final
LayerBuilder interface method - returning the layers at negative side.
- Parameters
gctx – the geometry context for this build call
-
void setConfiguration(const Config &config)
Set the configuration object.
- Parameters
config – is the configuration struct
-
void setLogger(std::unique_ptr<const Logger> newLogger)
Set logging instance.
Public Static Functions
-
struct Config
- #include <Acts/Plugins/TGeo/TGeoLayerBuilder.hpp>
nested configuration struct for steering of the layer builder
Public Members
-
bool autoSurfaceBinning = false
Automated binning & tolerances.
-
std::string configurationName = "undefined"
String based identification.
-
std::shared_ptr<const ITGeoDetectorElementSplitter> detectorElementSplitter = nullptr
Split TGeoElement if a splitter is provided.
-
ElementFactory elementFactory = defaultElementFactory
Factory for creating detector elements based on TGeoNodes.
-
std::shared_ptr<const ITGeoIdentifierProvider> identifierProvider = nullptr
Create an identifier from TGeoNode.
-
std::array<std::vector<LayerConfig>, 3> layerConfigurations
Configuration is always | n | c | p |.
-
std::shared_ptr<const LayerCreator> layerCreator = nullptr
Layer creator.
-
std::array<double, 3> layerSplitToleranceR = {-1., -1., -1.}
Split tolerances in R.
-
std::array<double, 3> layerSplitToleranceZ = {-1., -1., -1.}
Split tolerances in Z.
-
std::shared_ptr<const ProtoLayerHelper> protoLayerHelper = nullptr
ProtoLayer helper.
-
Acts::SurfaceBinningMatcher surfaceBinMatcher
The surface binning matcher.
-
double unit = 1 * UnitConstants::cm
Unit conversion.
-
bool autoSurfaceBinning = false
-
struct LayerConfig
- #include <Acts/Plugins/TGeo/TGeoLayerBuilder.hpp>
Helper config structs for volume parsing.
Public Types
-
using RangeConfig = std::pair<BinningValue, std::pair<double, double>>
-
using SplitConfig = std::pair<BinningValue, double>
Public Functions
-
inline LayerConfig()
Public Members
-
std::vector<std::pair<int, BinningType>> binning0 = {{-1, equidistant}}
Binning setup in l0: nbins (-1 -> automated), axis binning type.
-
std::vector<std::pair<int, BinningType>> binning1 = {{-1, equidistant}}
Binning setup in l1: nbins (-1 -> automated), axis binning type.
-
std::pair<double, double> envelope = {1 * UnitConstants::mm, 1 * UnitConstants::mm}
The envelope to be built around the layer.
-
std::string localAxes = "XYZ"
The local axis definition of TGeo object to Acts::Surface.
-
std::vector<RangeConfig> parseRanges = {}
Parse ranges: parameter and ranges.
-
std::vector<std::string> sensorNames = {}
Identify the sensor(s) by name.
-
std::vector<SplitConfig> splitConfigs = {}
Layer splitting: parameter and tolerance.
-
std::string volumeName = ""
Identify the search volume by name.
-
using RangeConfig = std::pair<BinningValue, std::pair<double, double>>
-
using ElementFactory = std::function<std::shared_ptr<TGeoDetectorElement>(const Identifier&, const TGeoNode&, const TGeoMatrix &tGeoMatrix, const std::string &axes, double scalor, std::shared_ptr<const Acts::ISurfaceMaterial> material)>
-
struct TGeoParser
- #include <Acts/Plugins/TGeo/TGeoParser.hpp>
TGeoParser is a helper struct that walks recursively through a TGeometry and selects by string comparison the TGeoNodes that match the criteria.
It also buils up the global transform for the conversion into an ACTS Surface
Public Types
-
using ParseRange = std::pair<double, double>
Public Static Functions
-
static void select(State &state, const Options &options, const TGeoMatrix &gmatrix = TGeoIdentity("ID"))
The parsing module, it takes the top Volume and recursively steps down.
- Parameters
state – [out] The parsing state configuration, passed through
options – [in] The parsing options as requiremed
gmatrix – The current built-up transform to global at this depth
-
struct Options
- #include <Acts/Plugins/TGeo/TGeoParser.hpp>
Nested configuration struct.
This contains the parsing configuration
Public Members
-
std::string localAxes = "XYZ"
The local axis definition of TGeo object wrt Acts::Surface.
-
std::vector<std::pair<BinningValue, ParseRange>> parseRanges = {}
Parse restrictions, several can apply.
-
std::vector<std::string> targetNames = {}
Identify the sensor(s)/target(s) by name.
-
double unit = 1 * UnitConstants::cm
Scaling from TGeo to ROOT.
-
std::vector<std::string> volumeNames = {}
Identify the volume by name.
-
std::string localAxes = "XYZ"
-
struct SelectedNode
- #include <Acts/Plugins/TGeo/TGeoParser.hpp>
Public Members
-
const TGeoNode *node = nullptr
-
std::unique_ptr<TGeoMatrix> transform = nullptr
-
const TGeoNode *node = nullptr
-
struct State
- #include <Acts/Plugins/TGeo/TGeoParser.hpp>
Nested state struct.
This is needed for the recursive parsing of the geometry, it collects the information during the parsing process and keeps track of the built up transform
Public Members
-
TGeoNode *node = nullptr
-
bool onBranch = false
-
std::vector<SelectedNode> selectedNodes = {}
-
TGeoVolume *volume = nullptr
-
TGeoNode *node = nullptr
-
using ParseRange = std::pair<double, double>
-
struct TGeoPrimitivesHelper
- #include <Acts/Plugins/TGeo/TGeoPrimitivesHelper.hpp>
Public Static Functions
-
static inline Transform3 makeTransform(const Eigen::Vector3d &rotationMatrixCol0, const Eigen::Vector3d &rotationMatrixCol1, const Eigen::Vector3d &rotationMatrixCol2, const Eigen::Vector3d &translation)
Helper method to create a transform from Rotation matrix vectors:
- Parameters
rotationMatrixCol0 –
rotationMatrixCol1 –
rotationMatrixCol2 – And translation
translation –
-
static bool match(const char *first, const char *second)
Private helper method : match string with wildcards.
- Parameters
first – is the one with the potential wildcard
second – is the test string
-
static bool match(const std::vector<std::string> &first, const char *second)
Private helper method : match string with wildcards Method that uses the match method with wild cards and performs it on an input list.
- Parameters
first – is the one with the potential wildcard
second – is the test string
-
static inline Transform3 makeTransform(const Eigen::Vector3d &rotationMatrixCol0, const Eigen::Vector3d &rotationMatrixCol1, const Eigen::Vector3d &rotationMatrixCol2, const Eigen::Vector3d &translation)
-
struct TGeoSurfaceConverter
- #include <Acts/Plugins/TGeo/TGeoSurfaceConverter.hpp>
Helper struct to convert TGeoShapes into Surface or Volume Bounds.
Public Static Functions
-
static std::tuple<std::shared_ptr<const CylinderBounds>, const Transform3, double> cylinderComponents(const TGeoShape &tgShape, const Double_t *rotation, const Double_t *translation, const std::string &axes, double scalor = 10.) noexcept(false)
Convert a TGeoShape into cylinder surface components.
- Parameters
tgShape – The TGeoShape
rotation – The rotation matrix as Double_t* from root
translation – The translation vector as Double_t* from root
axes – The axes definition
scalor – The unit scalor between TGeo and Acts
- Returns
tuple of DiscBounds, Transform, thickness
-
static std::tuple<std::shared_ptr<const DiscBounds>, const Transform3, double> discComponents(const TGeoShape &tgShape, const Double_t *rotation, const Double_t *translation, const std::string &axes, double scalor = 10.) noexcept(false)
Convert a TGeoShape into disk surface components.
- Parameters
tgShape – The TGeoShape
rotation – The rotation matrix as Double_t* from root
translation – The translation vector as Double_t* from root
axes – The axes definition
scalor – The unit scalor between TGeo and Acts
- Returns
tuple of DiscBounds, Transform, thickness
-
static std::tuple<std::shared_ptr<const PlanarBounds>, const Transform3, double> planeComponents(const TGeoShape &tgShape, const Double_t *rotation, const Double_t *translation, const std::string &axes, double scalor = 10.) noexcept(false)
Convert a TGeoShape into plane surface components.
- Parameters
tgShape – The TGeoShape
rotation – The rotation matrix as Double_t* from root
translation – The translation as a Double_t*
axes – The axes definition
scalor – The unit scalor between TGeo and Acts
- Returns
tuple of PlanarBounds, Transform, thickness
-
static inline double toRadian(double degree)
Translate TGeo degree [0, 360) to radian.
will correct to [-pi,pi)
- Parameters
degree – The input in degree
- Returns
angle in radians
-
static std::shared_ptr<Surface> toSurface(const TGeoShape &tgShape, const TGeoMatrix &tgMatrix, const std::string &axes, double scalor = 10.) noexcept(false)
Convert a TGeoShape to a Surface.
- Parameters
tgShape – The TGeoShape
tgMatrix – The matrix representing the tranbsform
axes – The axes definition
scalor – The unit scalor between TGeo and Acts
- Returns
shared pointer to a surface
-
static std::tuple<std::shared_ptr<const CylinderBounds>, const Transform3, double> cylinderComponents(const TGeoShape &tgShape, const Double_t *rotation, const Double_t *translation, const std::string &axes, double scalor = 10.) noexcept(false)
-
class TorchEdgeClassifier : public Acts::EdgeClassificationBase
- #include <Acts/Plugins/ExaTrkX/TorchEdgeClassifier.hpp>
Public Functions
-
~TorchEdgeClassifier()
-
inline Config config() const
-
virtual std::tuple<std::any, std::any, std::any> operator()(std::any nodes, std::any edges) override
Perform edge classification.
- Parameters
nodes – Node tensor with shape (n_nodes, n_node_features)
edges – Edge-index tensor with shape (2, n_edges)
- Returns
(node_tensor, edge_tensor, score_tensor)
-
struct Config
- #include <Acts/Plugins/ExaTrkX/TorchEdgeClassifier.hpp>
Public Members
-
float cut = 0.21
-
std::string modelPath
-
int nChunks = 1
-
int numFeatures = 3
-
bool undirected = false
-
float cut = 0.21
-
~TorchEdgeClassifier()
-
class TorchMetricLearning : public Acts::GraphConstructionBase
- #include <Acts/Plugins/ExaTrkX/TorchMetricLearning.hpp>
Public Functions
-
~TorchMetricLearning()
-
inline Config config() const
-
virtual std::tuple<std::any, std::any> operator()(std::vector<float> &inputValues, std::size_t numNodes) override
Perform the graph construction.
- Parameters
inputValues – Flattened input data
numNodes – number of nodes. inputValues.size() / numNodes then gives the number of features
- Returns
(node_tensor, edge_tensore)
-
struct Config
- #include <Acts/Plugins/ExaTrkX/TorchMetricLearning.hpp>
Public Members
-
int embeddingDim = 8
-
int knnVal = 500
-
std::string modelPath
-
int numFeatures = 3
-
float rVal = 1.6
-
bool shuffleDirections = false
-
int embeddingDim = 8
-
~TorchMetricLearning()
-
template<typename T, bool ReadOnly>
struct TrackAccessorBase - #include <Acts/EventData/TrackContainer.hpp>
Utility class that eases accessing dynamic columns in track containers.
- Template Parameters
T – the type of the value to access
ReadOnly – true if this is a const accessor
Public Functions
-
inline TrackAccessorBase(const std::string &_key)
Create the accessor from a string key.
- Parameters
_key – the key
-
inline TrackAccessorBase(HashedString _key)
Create the accessor from an already-hashed string key.
- Parameters
_key – the key
-
template<typename track_proxy_t, bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline T &operator()(track_proxy_t track) const Access the stored key on the track given as an argument.
Mutable version
- Template Parameters
track_proxy_t – the type of the track proxy
- Parameters
track – the track to access
- Returns
mutable reference to the column behind the key
-
template<typename track_proxy_t, bool RO = ReadOnly, typename = std::enable_if_t<RO>>
inline const T &operator()(track_proxy_t track) const Access the stored key on the track given as an argument.
COnst version
- Template Parameters
track_proxy_t – the type of the track proxy
- Parameters
track – the track to access
- Returns
const reference to the column behind the key
Public Members
-
HashedString key
-
template<typename input_track_t>
class TrackAtVertex - #include <Acts/Vertexing/TrackAtVertex.hpp>
Defines a track at vertex object.
- Template Parameters
input_track_t – Track object type
Public Functions
-
TrackAtVertex() = delete
Deleted default constructor.
-
inline TrackAtVertex(const BoundTrackParameters ¶msAtVertex, const input_track_t *originalTrack)
Constructor with default chi2.
- Parameters
paramsAtVertex – Fitted perigee parameter
originalTrack – Original perigee parameter
-
inline TrackAtVertex(double chi2perTrack, const BoundTrackParameters ¶msAtVertex, const input_track_t *originalTrack)
Parameterized constructor.
- Parameters
chi2perTrack – Chi2 of track
paramsAtVertex – Fitted perigee parameter
originalTrack – Original perigee parameter
Public Members
-
double chi2Track = 0
Chi2 of track.
-
BoundTrackParameters fittedParams
Fitted perigee.
-
bool isLinearized = false
Is already linearized.
-
LinearizedTrack linearizedState
The linearized state of the track at vertex.
-
double ndf = 0
Number degrees of freedom Note: Can be different from integer value since annealing can result in effective non-interger values.
-
const input_track_t *originalParams
Original input parameters.
-
double trackWeight = 1
Weight of track in fit.
-
double vertexCompatibility = 0
Value of the compatibility of the track to the actual vertex, based on the estimation of the 3d distance between the track and the vertex.
-
class TrackBuildingBase
- #include <Acts/Plugins/ExaTrkX/Stages.hpp>
Subclassed by Acts::BoostTrackBuilding, Acts::CugraphTrackBuilding
Public Functions
-
virtual ~TrackBuildingBase() = default
-
virtual std::vector<std::vector<int>> operator()(std::any nodes, std::any edges, std::any edgeWeights, std::vector<int> &spacepointIDs) = 0
Perform track building.
- Parameters
nodes – Node tensor with shape (n_nodes, n_node_features)
edges – Edge-index tensor with shape (2, n_edges)
edgeWeights – Edge-weights of the previous edge classification phase
spacepointIDs – IDs of the nodes (must have size=n_nodes)
- Returns
tracks (as vectors of node-IDs)
-
virtual ~TrackBuildingBase() = default
-
template<ACTS_CONCEPT track_container_t(TrackContainerBackend), typename traj_t, template<typename> class holder_t = detail::RefHolder>
class TrackContainer - #include <Acts/EventData/TrackContainer.hpp>
Track container interface class.
This type represents a collections of tracks. It uses a backend to store both the actual tracks and the associated track states.
- Template Parameters
track_container_t – the track container backend
traj_t – the track state container backend
holder_t – ownership management class for the backend
Public Types
-
using ConstTrackProxy = Acts::TrackProxy<track_container_t, traj_t, holder_t, true>
-
using IndexType = TrackIndexType
-
using TrackProxy = Acts::TrackProxy<track_container_t, traj_t, holder_t, false>
Public Functions
-
template<template<typename> class H = holder_t, bool RO = (IsReadOnlyTrackContainer<track_container_t>::value && IsReadOnlyMultiTrajectory<traj_t>::value), typename = std::enable_if_t<detail::is_same_template<H, detail::ConstRefHolder>::value && RO>>
inline TrackContainer(const track_container_t &container, const traj_t &traj) Constructor from const references to a track container backend and to a track state container backend.
Note
The track container will not assume ownership over the backends in this case. You need to ensure suitable lifetime
- Parameters
container – the track container backend
traj – the track state container backend
-
inline TrackContainer(holder_t<track_container_t> container, holder_t<traj_t> traj)
Constructor from a track container backend and a track state container backend.
- Parameters
container – the track container backend
traj – the track state container backend
-
template<template<typename> class H = holder_t, typename = std::enable_if_t<detail::is_same_template<H, detail::RefHolder>::value>>
inline TrackContainer(track_container_t &container, traj_t &traj) Constructor from references to a track container backend and to a track state container backend.
Note
The track container will not assume ownership over the backends in this case. You need to ensure suitable lifetime
- Parameters
container – the track container backend
traj – the track state container backend
-
template<typename T, bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline constexpr void addColumn(const std::string &key) Add a dymanic column to the track container.
- Parameters
key – the name of the column to be added
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline IndexType addTrack() Add a track to the container.
Note this only creates the logical track and allocates memory. You can combine this with
getTrackto obtain a track proxy- Returns
the index to the newly added track
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline auto begin() Get a mutable iterator to the first track in the container.
- Returns
a mutable iterator to the first track
-
inline auto begin() const
Get an const iterator to the first track in the container.
- Returns
a const iterator to the first track
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline void clear() Clear the content of the track container.
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline auto &container() Get a mutable reference to the track container backend.
- Returns
a mutable reference to the backend
-
inline const auto &container() const
Get a const reference to the track container backend.
- Returns
a const reference to the backend
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline auto end() Get a past-the-end iterator for this container.
- Returns
a past-the-end iterator
-
inline auto end() const
Get a past-the-end iterator for this container.
- Returns
a past-the-end iterator
-
template<typename other_track_container_t, bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline void ensureDynamicColumns(const other_track_container_t &other) Helper function to make this track container match the dynamic columns of another one.
This will only work if the track container supports this source, and depends on the implementation details of the dynamic columns of the container
- Template Parameters
other_track_container_t – Type of the other track container
- Parameters
other – The other track container
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline TrackProxy getTrack(IndexType itrack) Get a mutable track proxy for a track index.
- Parameters
itrack – the track index in the container
- Returns
A mutable track proxy for the index
-
inline ConstTrackProxy getTrack(IndexType itrack) const
Get a const track proxy for a track index.
- Parameters
itrack – the track index in the container
- Returns
A const track proxy for the index
-
inline constexpr bool hasColumn(const std::string &key) const
Check if this track container has a specific dynamic column.
- Parameters
key – the key to check for
-
inline constexpr bool hasColumn(HashedString key) const
Check if a this track container has a specific dynamic column.
- Parameters
key – the key to check for
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline void removeTrack(IndexType itrack) Remove a track at index
itrackfrom the container.Note
This invalidates all track proxies!
- Parameters
itrack – The index of the track to remove
-
inline constexpr IndexType size() const
Get the size of the track container.
- Returns
the sixe
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline auto &trackStateContainer() Get a mutable reference to the track state container backend.
- Returns
a mutable reference to the backend
-
inline const auto &trackStateContainer() const
Get a const reference to the track state container backend.
- Returns
a const reference to the backend
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline auto &trackStateContainerHolder() Retrieve the holder of the track state container.
- Returns
The track state container including it’s holder
-
inline const auto &trackStateContainerHolder() const
Retrieve the holder of the track state container.
- Returns
The track state container including it’s holder
Public Static Attributes
-
static constexpr IndexType kInvalid = kTrackIndexInvalid
-
static constexpr bool ReadOnly = IsReadOnlyTrackContainer<track_container_t>::value
-
static constexpr bool TrackStateReadOnly = IsReadOnlyMultiTrajectory<traj_t>::value
-
template<typename vfitter_t, typename track_density_t = GaussianTrackDensity<typename vfitter_t::InputTrack_t>>
class TrackDensityVertexFinder - #include <Acts/Vertexing/TrackDensityVertexFinder.hpp>
Finds a vertex seed based on the maximum of a track density function.
Each track is modelled as a 2d density function around its d0/z0 perigee parameter values. The z seed position is then found as the position of the maximum of all summed track density functions.
Ref. (1): https://cds.cern.ch/record/2670380
- Template Parameters
vfitter_t – The vertex fitter type (needed to fulfill concept)
track_density_t – The track density type
Public Functions
-
template<typename T = InputTrack_t, std::enable_if_t<std::is_same<T, BoundTrackParameters>::value, int> = 0>
inline TrackDensityVertexFinder() Default constructor used if InputTrack_t type == BoundTrackParameters.
-
template<typename T = InputTrack_t, std::enable_if_t<std::is_same<T, BoundTrackParameters>::value, int> = 0>
inline TrackDensityVertexFinder(const Config &cfg) Constructor used if InputTrack_t type == BoundTrackParameters.
- Parameters
cfg – Configuration object
-
inline TrackDensityVertexFinder(const Config &cfg, const std::function<BoundTrackParameters(InputTrack_t)> &func)
Constructor for user-defined InputTrack_t type =! BoundTrackParameters.
- Parameters
cfg – Configuration object
func – Function extracting BoundTrackParameters from InputTrack_t object
-
inline TrackDensityVertexFinder(const std::function<BoundTrackParameters(InputTrack_t)> &func)
Constructor for user-defined InputTrack_t type =! BoundTrackParameters with default Config object.
- Parameters
func – Function extracting BoundTrackParameters from InputTrack_t object
-
Result<std::vector<Vertex<InputTrack_t>>> find(const std::vector<const InputTrack_t*> &trackVector, const VertexingOptions<InputTrack_t> &vertexingOptions, State &state) const
Function that finds single vertex candidate.
- Parameters
trackVector – Input track collection
vertexingOptions – Vertexing options
state – State for fulfilling interfaces
- Returns
Vector of vertices, filled with a single vertex (for consistent interfaces)
-
struct Config
- #include <Acts/Vertexing/TrackDensityVertexFinder.hpp>
The Config struct.
Public Members
-
track_density_t trackDensityEstimator
-
track_density_t trackDensityEstimator
-
struct State
- #include <Acts/Vertexing/TrackDensityVertexFinder.hpp>
State struct for fulfilling interface.
-
class TrackingGeometry
- #include <Acts/Geometry/TrackingGeometry.hpp>
The TrackingGeometry class is the owner of the constructed TrackingVolumes.
It enables both, a global search for an asociatedVolume (respectively, if existing, a global search of an associated Layer or the next associated Layer), such as a continuous navigation by BoundarySurfaces between the confined TrackingVolumes.
Public Functions
-
TrackingGeometry(const MutableTrackingVolumePtr &highestVolume, const IMaterialDecorator *materialDecorator = nullptr, const GeometryIdentifierHook &hook = {}, const Logger &logger = getDummyLogger())
Constructor.
- Parameters
highestVolume – is the world volume
materialDecorator – is a dediated decorator that can assign surface or volume based material to the TrackingVolume
hook – Identifier hook to be applied to surfaces
logger – instance of a logger (defaulting to the “silent” one)
-
~TrackingGeometry()
Destructor.
-
const Layer *associatedLayer(const GeometryContext &gctx, const Vector3 &gp) const
Forward the associated Layer information.
- Parameters
gctx – is the context for this request (e.g. alignment)
gp – is the global position of the call
- Returns
plain pointer to assocaiated layer
-
const Surface *findSurface(GeometryIdentifier id) const
Search for a surface with the given identifier.
- Parameters
id – is the geometry identifier of the surface
- Return values
nullptr – if no such surface exists
pointer – to the found surface otherwise.
-
const TrackingVolume *findVolume(GeometryIdentifier id) const
Search for a volume with the given identifier.
- Parameters
id – is the geometry identifier of the volume
- Return values
nullptr – if no such volume exists
pointer – to the found volume otherwise.
-
const Surface *getBeamline() const
surface representing the beam pipe
Note
The ownership is not passed, e.g. do not delete the pointer
- Returns
raw pointer to surface representing the beam pipe (could be a null pointer)
-
const TrackingVolume *highestTrackingVolume() const
Access to the world volume.
- Returns
plain pointer to the world volume
Access to the world volume.
- Returns
shared pointer to the world volume
-
const TrackingVolume *lowestTrackingVolume(const GeometryContext &gctx, const Vector3 &gp) const
return the lowest tracking Volume
- Parameters
gctx – The current geometry context object, e.g. alignment
gp – is the global position of the call
- Returns
plain pointer to the lowest TrackingVolume
Register the beam tube.
- Parameters
beam – is the beam line surface
-
template<ACTS_CONCEPT visitor_t(SurfaceVisitor)>
inline void visitSurfaces(visitor_t &&visitor) const Visit all sensitive surfaces.
- Template Parameters
visitor_t – Type of the callable visitor
- Parameters
visitor – The callable. Will be called for each sensitive surface that is found
-
TrackingGeometry(const MutableTrackingVolumePtr &highestVolume, const IMaterialDecorator *materialDecorator = nullptr, const GeometryIdentifierHook &hook = {}, const Logger &logger = getDummyLogger())
-
class TrackingGeometryBuilder : public Acts::ITrackingGeometryBuilder
- #include <Acts/Geometry/TrackingGeometryBuilder.hpp>
The Acts::TrackingGeometry Builder for volumes that wrap around another.
It retrieves an array of std::functions that build the TrackingGeometry sequentially in order, with the following options:
contained (e.g. a final insertion of a beam pipe of longer extend)
wrapped (e.g. an outer detector wrapping an inner one)
attached (e.g. a neighbor detector attaching to the previous one)
The returned volume of each step must be processable by the previous step
Public Functions
-
TrackingGeometryBuilder(const Config &cgbConfig, std::unique_ptr<const Logger> logger = getDefaultLogger("TrackingGeometryBuilder", Logging::INFO))
Constructor.
- Parameters
cgbConfig – [in] is the configuration struct for this builder
logger – [in] logging instance
-
~TrackingGeometryBuilder() override = default
Destructor.
-
const Config &getConfiguration() const
Get configuration method.
- Returns
the current configuration
-
void setConfiguration(const Config &cgbConfig)
Set configuration method.
- Parameters
cgbConfig – is the new configuration struct
-
void setLogger(std::unique_ptr<const Logger> newLogger)
set logging instance
- Parameters
newLogger – the new logging instance
-
virtual std::unique_ptr<const TrackingGeometry> trackingGeometry(const GeometryContext &gctx) const final
TrackingGeometry Interface method.
- Parameters
gctx – geometry context of that building call
- Returns
a unique pointer to a TrackingGeometry
-
struct Config
- #include <Acts/Geometry/TrackingGeometryBuilder.hpp>
Nested Configuration for the CylinderVolumeBuilder.
Public Members
-
std::shared_ptr<const GeometryIdentifierHook> geometryIdentifierHook = std::make_shared<GeometryIdentifierHook>()
Optional geometry identifier hook to be used during closure.
-
std::shared_ptr<const IMaterialDecorator> materialDecorator = nullptr
The optional material decorator for this.
- std::vector< std::function< std::shared_ptr< TrackingVolume > const GeometryContext &gctx, const TrackingVolumePtr &, const VolumeBoundsPtr &)> > trackingVolumeBuilders
The list of tracking volume builders.
-
std::shared_ptr<const ITrackingVolumeHelper> trackingVolumeHelper = nullptr
The tracking volume helper for detector construction.
-
std::shared_ptr<const GeometryIdentifierHook> geometryIdentifierHook = std::make_shared<GeometryIdentifierHook>()
-
class TrackingVolume : public Acts::Volume
- #include <Acts/Geometry/TrackingVolume.hpp>
Full Volume description used in Tracking, it inherits from Volume to get the geometrical structure.
information / internal navigation with in 5 different ways:A TrackingVolume at navigation level can provide the (layer) material
The TrackingVolume can also be a simple container of other TrackingVolumes--- a) Static confinement of Layers --- b) detached sub volumes --- b) unordered (arbitrarily oriented) layers --- d) unordered sub volumes --- e) unordered layers AND unordered subvolumes
In addition it is capable of holding a subarray of Layers and TrackingVolumes.
Public Functions
-
TrackingVolume() = delete
-
TrackingVolume(const TrackingVolume&) = delete
-
~TrackingVolume() override
Set the boundary surface material description.
The material is usually derived in a complicated way and loaded from a framework given source. As various volumes could potentially share the the same material description, it is provided as a shared object
- Parameters
surfaceMaterial – Material description of this volume
bsFace – Specifies which boundary surface to assign the material to
Set the volume material description.
The material is usually derived in a complicated way and loaded from a framework given source. As various volumes could potentially share the the same material description, it is provided as a shared object
- Parameters
material – Material description of this volume
-
const Layer *associatedLayer(const GeometryContext &gctx, const Vector3 &position) const
Return the associated Layer to the global position.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the associated global position
- Returns
plain pointer to layer object
-
const TrackingVolumeBoundaries &boundarySurfaces() const
Method to return the BoundarySurfaces.
-
inline unsigned int colorCode() const
Get the color code.
Returns all boundary surfaces sorted by the user.
- Template Parameters
options_t – Type of navigation options object for decomposition
sorter_t – Type of the boundary surface sorter
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The position for searching
direction – The direction for searching
options – The templated navigation options
logger – A
Loggerinstance
- Returns
is the templated boundary intersection
Resolves the volume into (compatible) Layers.
This is the method for the propagator/extrapolator
- Template Parameters
options_t – Type of navigation options object for decomposition
- Parameters
gctx – The current geometry context object, e.g. alignment
position – Position for the search
direction – Direction for the search
options – The templated navigation options
- Returns
vector of compatible intersections with layers
Return surfaces in given direction from bounding volume hierarchy.
- Template Parameters
options_t – Type of navigation options object for decomposition
- Parameters
gctx – The current geometry context object, e.g. alignment
position – The position to start from
direction – The direction towards which to test
angle – The opening angle
options – The templated navigation options
- Returns
Vector of surface candidates
-
inline const LayerArray *confinedLayers() const
Return the confined static layer array - if it exists.
- Returns
the BinnedArray of static layers if exists
-
inline std::shared_ptr<const TrackingVolumeArray> confinedVolumes() const
Return the confined volumes of this container array - if it exists.
-
inline const MutableTrackingVolumeVector denseVolumes() const
Return the confined dense volumes.
-
void glueTrackingVolume(const GeometryContext &gctx, BoundarySurfaceFace bsfMine, TrackingVolume *neighbor, BoundarySurfaceFace bsfNeighbor)
Glue another tracking volume to this one.
if common face is set the glued volumes are sharing the boundary, down to the last navigation volume
- Parameters
gctx – The current geometry context object, e.g. alignment
bsfMine – is the boundary face indicater where to glue
neighbor – is the TrackingVolume to be glued
bsfNeighbor – is the boundary surface of the neighbor
Glue another tracking volume to this one.
if common face is set the glued volumes are sharing the boundary, down to the last navigation volume
- Parameters
gctx – The current geometry context object, e.g. alignment
bsfMine – is the boundary face indicater where to glue
neighbors – are the TrackingVolumes to be glued
bsfNeighbor – are the boundary surface of the neighbors
-
GlueVolumesDescriptor &glueVolumesDescriptor()
Register the outside glue volumes - ordering is in the TrackingVolume Frame:
negativeFaceXY
(faces YZ, ZY, radial faces)
positiveFaceXY
-
inline bool hasBoundingVolumeHierarchy() const
Return whether this TrackingVolume has a BoundingVolumeHierarchy associated.
- Returns
If it has a BVH or not.
-
const TrackingVolume *lowestTrackingVolume(const GeometryContext &gctx, const Vector3 &position, const double tol = 0.) const
Return the associated sub Volume, returns THIS if no subVolume exists.
- Parameters
gctx – The current geometry context object, e.g. alignment
position – is the global position associated with that search
tol – Search position tolerance for dense volumes
- Returns
plain pointer to associated with the position
-
inline const TrackingVolume *motherVolume() const
Return the MotherVolume - if it exists.
-
TrackingVolume &operator=(const TrackingVolume&) = delete
-
inline void registerColorCode(unsigned int icolor)
Register the color code.
- Parameters
icolor – is a color number
-
void registerGlueVolumeDescriptor(GlueVolumesDescriptor *gvd)
Register the outside glue volumes - ordering is in the TrackingVolume Frame:
negativeFaceXY
(faces YZ, ZY, radial faces)
positiveFaceXY
- Parameters
gvd – register a new GlueVolumeDescriptor
-
inline void setMotherVolume(const TrackingVolume *mvol)
Set the MotherVolume.
- Parameters
mvol – is the mother volume
Provide a new BoundarySurface from the glueing.
- Parameters
bsf – is the boundary face indicater where to glue
bs – is the new boundary surface
checkmaterial – is a flag how to deal with material, if true:
if the old boundary surface had a material description but the new one has not, keep the current one
in all other cases just assign the new boundary surface
-
template<ACTS_CONCEPT visitor_t(SurfaceVisitor)>
inline void visitSurfaces(visitor_t &&visitor) const Visit all sensitive surfaces.
If a context is needed for the visit, the vistitor has to provide this e.g. as a private member
- Template Parameters
visitor_t – Type of the callable visitor
- Parameters
visitor – The callable. Will be called for each sensitive surface that is found
-
inline const IVolumeMaterial *volumeMaterial() const
Return the material of the volume.
Return the material of the volume as shared pointer.
-
inline const std::string &volumeName() const
Returns the VolumeName - for debug reason, might be depreciated later.
Public Static Functions
Factory constructor for Tracking Volume with a bounding volume hierarchy.
- Parameters
transform – is the global 3D transform to position the volume in space
volbounds – is the description of the volume boundaries
boxStore – Vector owning the contained bounding boxes
descendants – Vector owning the child volumes
top – The top of the hierarchy (top node)
volumeMaterial – is the materials of the tracking volume
volumeName – is a string identifier
- Returns
shared pointer to a new TrackingVolume
Factory constructor for a container TrackingVolume.
by definition a Vacuum volume
- Parameters
transform – is the global 3D transform to position the volume in space
volumeBounds – is the description of the volume boundaries
containedVolumes – are the static volumes that fill this volume
volumeName – is a string identifier
- Returns
shared pointer to a new TrackingVolume
Factory constructor for Tracking Volumes with content.
can not be a container volume
- Parameters
transform – is the global 3D transform to position the volume in space
volumeBounds – is the description of the volume boundaries
volumeMaterial – is are materials of the tracking volume
containedLayers – is the confined layer array (optional)
containedVolumes – is the confined volume array (optional)
denseVolumes – is the array of dense volulmes (optional)
volumeName – is a string identifier
- Returns
shared pointer to a new TrackingVolume
-
TrackingVolume() = delete
-
class TrackingVolumeArrayCreator : public Acts::ITrackingVolumeArrayCreator
- #include <Acts/Geometry/TrackingVolumeArrayCreator.hpp>
The TrackingVolumeArrayCreator is a simple Tool that helps to construct binned arrays of TrackingVolumes for both, confinement in another volume and navigation issues.
Public Functions
-
inline TrackingVolumeArrayCreator(const Config&, std::unique_ptr<const Logger> logger = getDefaultLogger("LayerArrayCreator", Logging::INFO))
Constructor.
- Parameters
logger – logging instance
-
~TrackingVolumeArrayCreator() override = default
Destructor.
-
inline void setLogger(std::unique_ptr<const Logger> logger)
Set logging instance.
- Parameters
logger – is the logging instance to be set
-
virtual std::shared_ptr<const TrackingVolumeArray> trackingVolumeArray(const GeometryContext &gctx, const TrackingVolumeVector &tVolumes, BinningValue bValue) const override
create a tracking volume array
- Parameters
gctx – [in] the geometry context for this building
tVolumes – [in] is the vector of TrackingVolumes to be
bValue – [in] is the binning value
- Returns
new created volume array
-
struct Config
- #include <Acts/Geometry/TrackingVolumeArrayCreator.hpp>
This struct stores the configuration of the tracking geometry.
-
inline TrackingVolumeArrayCreator(const Config&, std::unique_ptr<const Logger> logger = getDefaultLogger("LayerArrayCreator", Logging::INFO))
-
template<typename track_container_t, typename trajectory_t, template<typename> class holder_t, bool read_only = true>
class TrackProxy - #include <Acts/EventData/TrackProxy.hpp>
Proxy class representing a single track.
- Template Parameters
track_container_t – the container backend
trajectory_t – the track state container backend
holder_t – ownership management class for the backend
read_only – true if this track container is not mutable
Public Types
-
using ConstCovariance = typename detail_lt::Types<eBoundSize, true>::CovarianceMap
-
using ConstParameters = typename detail_lt::Types<eBoundSize, true>::CoefficientsMap
-
using ConstTrackProxy = TrackProxy<track_container_t, trajectory_t, holder_t, true>
-
using ConstTrackStateProxy = typename Trajectory::ConstTrackStateProxy
-
using Container = track_container_t
-
using Covariance = typename detail_lt::Types<eBoundSize, false>::CovarianceMap
-
using IndexType = typename Container::IndexType
-
using MutableTrackProxy = TrackProxy<track_container_t, trajectory_t, holder_t, false>
-
using Parameters = typename detail_lt::Types<eBoundSize, false>::CoefficientsMap
-
using TrackStateProxy = typename Trajectory::TrackStateProxy
-
using Trajectory = trajectory_t
Public Functions
-
inline TrackProxy(const MutableTrackProxy &other)
Copy constructor from a mutable track proxy.
This is always valid, either mutable to mutable or mutable to const
- Parameters
other – the other track state proxy
-
inline ActsScalar absoluteMomentum() const
Get the absolute momentum of the tack.
- Returns
The absolute track momentum
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline auto appendTrackState(TrackStatePropMask mask = TrackStatePropMask::All) Append a track state to this track.
This will modify the tip index to point at the newly created track state, which will be directly after the previous track state at tip index.
- Parameters
mask – The allocation prop mask for the new track state
- Returns
The newly added track state
-
inline ActsScalar charge() const
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline float &chi2() Return a mutable reference to the chi squared Mutable version.
- Returns
The chi squared
-
inline float chi2() const
Return the chi squared for the track.
Const version
- Returns
The chi squared
-
template<typename T, HashedString key, bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline constexpr T &component() Retrieve a mutable reference to a component.
- Template Parameters
T – The type of the component to access
key – String key for the component to access
- Returns
Mutable reference to the component given by
key
-
template<typename T, HashedString key>
inline constexpr const T &component() const Retrieve a const reference to a component.
- Template Parameters
T – The type of the component to access
key – String key for the component to access
- Returns
Const reference to the component given by
key
-
template<typename T, bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline constexpr T &component(HashedString key) Retrieve a mutable reference to a component.
- Template Parameters
T – The type of the component to access
- Parameters
key – String key for the component to access
- Returns
Mutable reference to the component given by
key
-
template<typename T>
inline constexpr const T &component(HashedString key) const Retrieve a const reference to a component.
- Template Parameters
T – The type of the component to access
- Parameters
key – String key for the component to access
- Returns
Const reference to the component given by
key
-
template<typename T, bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline constexpr T &component(std::string_view key) Retrieve a mutable reference to a component.
Note
This might hash the
keyat runtime instead of compile-time- Template Parameters
T – The type of the component to access
- Parameters
key – String key for the component to access
- Returns
Mutable reference to the component given by
key
-
template<typename T>
inline constexpr const T &component(std::string_view key) const Retrieve a const reference to a component.
Note
This might hash the
keyat runtime instead of compile-time- Template Parameters
T – The type of the component to access
- Parameters
key – String key for the component to access
- Returns
Const reference to the component given by
key
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline auto &container() Return a reference to the track container backend, mutable version.
- Returns
reference to the track container backend
-
inline const auto &container() const
Return a reference to the track container backend, const version.
- Returns
reference to the track container backend
-
template<typename track_proxy_t, bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline void copyFrom(const track_proxy_t &other, bool copyTrackStates = true) Copy the content of another track proxy into this one.
- Template Parameters
track_proxy_t – the other track proxy’s type
- Parameters
other – The the track proxy
copyTrackStates – Copy the track state sequence from
other
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline Covariance covariance() Get the covariance of the track at the reference surface (e.g.
perigee). Mutable version
- Returns
Proxy matrix for the covariance
-
inline ConstCovariance covariance() const
Get the covariance of the track at the reference surface (e.g.
perigee). Const version
- Returns
Proxy matrix for the covariance
-
inline Vector3 direction() const
Get a unit vector along the track direction at the reference surface.
- Returns
The direction unit vector
-
inline bool hasReferenceSurface() const
Return whether a reference surface is associated to this track.
- Returns
whether a surface exists or not
-
inline IndexType index() const
Return the index of this track in the track container.
Note
This is separate from the tip index
- Returns
the track index
-
inline ActsScalar loc0() const
Access the loc0 parameter of the track at the reference surface.
- Returns
The loc0 parameter
-
inline ActsScalar loc1() const
Access the loc1 parameter of the track at the reference surface.
- Returns
The loc1 parameter
-
inline Vector3 momentum() const
Get the global momentum vector.
- Returns
the global momentum vector
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline unsigned int &nDoF() Return a mutable reference to the number of degrees of freedom for the track.
Mutable version
- Returns
The the number of degrees of freedom
-
inline unsigned int nDoF() const
Return the number of degrees of freedom for the track.
Const version
- Returns
The number of degrees of freedom
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline unsigned int &nHoles() Return a mutable reference to the number of holes for the track.
Mutable version
- Returns
The number of holes
-
inline unsigned int nHoles() const
Return the number of measurements for the track.
Const version
- Returns
The number of measurements
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline unsigned int &nMeasurements() Return the number of measurements for the track.
Const version
- Returns
The number of measurements
-
inline unsigned int nMeasurements() const
Return a mutable reference to the number of measurements for the track.
Mutable version
- Returns
The number of measurements
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline unsigned int &nOutliers() Return a mutable reference to the number of outliers for the track.
Mutable version
- Returns
The number of outliers
-
inline unsigned int nOutliers() const
Return the number of outliers for the track.
Const version
- Returns
The number of outliers
Return a mutable reference to the number of shared hits for the track.
Mutable version
- Returns
The number of shared hits
Return the number of shared hits for the track.
Const version
- Returns
The number of shared hits
-
inline unsigned int nTrackStates() const
Return the number of track states associated to this track.
Note
This is calculated by iterating over the track states which is somewhat expensive. Consider caching this value if you need It more than once.
- Returns
The number of track states
-
inline TrackProxy &operator=(const MutableTrackProxy &other)
Copy assignment operator from mutable track proxy.
This is always valid, either mutable to mutable or mutable to const
- Parameters
other – the other track state proxy
-
inline bool operator==(const TrackProxy &other) const
Equality operator with another track proxy Checks the container identity and the track index.
- Returns
True if the track proxies refer to the same track
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline Parameters parameters() Get the parameters of the track at the reference surface (e.g.
perigee). Mutable version
- Returns
Proxy vector for the parameters
-
inline ConstParameters parameters() const
Get the parameters of the track at the reference surface (e.g.
perigee). Const version
- Returns
Proxy vector for the parameters
-
inline ActsScalar phi() const
Access the phi parameter of the track at the reference surface.
- Returns
The phi parameter
-
inline ActsScalar qOverP() const
Access the q/p (curvature) parameter of the track at the reference surface.
- Returns
The q/p parameter
-
inline const Surface &referenceSurface() const
Get the reference surface of the track (e.g.
the perigee)
- Returns
the reference surface
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline void reverseTrackStates() Reverse the ordering of track states for this track Afterwards, the previous endpoint of the track state sequence will be the “innermost” track state.
Note
This is dangerous with branching track state sequences, as it will break them
Set a new reference surface for this track.
- Parameters
srf – The surface to set
-
inline ActsScalar theta() const
Access the theta parameter of the track at the reference surface.
- Returns
The theta parameter
-
inline ActsScalar time() const
Access the time parameter of the track at the reference surface.
- Returns
The time parameter
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline IndexType &tipIndex() Get a mutable reference to the tip index, i.e.
the entry point into the track container
- Returns
mutable reference to the tip index
-
inline IndexType tipIndex() const
Get the tip index, i.e.
the entry point into the track state container
- Returns
the tip index by value
-
template<bool RO = ReadOnly, typename = std::enable_if_t<!RO>>
inline auto trackStates() Get a range over the track states of this track.
Return value is compatible with range based for loop. Mutable version
- Returns
Track state range to iterate over
-
inline auto trackStates() const
Get a range over the track states of this track.
Return value is compatible with range based for loop. Const version
- Returns
Track state range to iterate over
-
inline ActsScalar transverseMomentum() const
Get the transverse momentum of the track.
- Returns
The track transverse momentum value
Public Static Attributes
-
static constexpr bool ReadOnly = read_only
Friends
- friend class TrackProxy
-
class TrackSelector
- #include <Acts/TrackFinding/TrackSelector.hpp>
Class which performs filtering of tracks.
It accepts an input and an output track container and uses the built-in copy facility to copy tracks into the output container.
Public Functions
-
inline TrackSelector(const Config &config)
Constructor from a config object.
- Parameters
config – is the configuration object
-
inline const Config &config() const
Get readonly access to the config parameters.
- Returns
the config object
-
template<typename track_proxy_t>
bool isValidTrack(const track_proxy_t &track) const Helper function to check if a track is valid.
- Template Parameters
track_proxy_t – is the type of the track proxy
- Parameters
track – is the track proxy
- Returns
true if the track is valid
-
template<typename input_tracks_t, typename output_tracks_t>
void selectTracks(const input_tracks_t &inputTracks, output_tracks_t &outputTracks) const Select tracks from an input container and copy them into an output container.
- Template Parameters
input_tracks_t – is the type of the input track container
output_tracks_t – is the type of the output track container
- Parameters
inputTracks – is the input track container
outputTracks – is the output track container
-
struct Config
- #include <Acts/TrackFinding/TrackSelector.hpp>
Public Members
-
double absEtaMax = std::numeric_limits<double>::infinity()
-
double absEtaMin = 0.0
-
double etaMax = std::numeric_limits<double>::infinity()
-
double etaMin = -std::numeric_limits<double>::infinity()
-
double loc0Max = std::numeric_limits<double>::infinity()
-
double loc0Min = -std::numeric_limits<double>::infinity()
-
double loc1Max = std::numeric_limits<double>::infinity()
-
double loc1Min = -std::numeric_limits<double>::infinity()
-
std::size_t minMeasurements = 0
-
double phiMax = std::numeric_limits<double>::infinity()
-
double phiMin = -std::numeric_limits<double>::infinity()
-
double ptMax = std::numeric_limits<double>::infinity()
-
double ptMin = 0.0
-
double timeMax = std::numeric_limits<double>::infinity()
-
double timeMin = -std::numeric_limits<double>::infinity()
-
double absEtaMax = std::numeric_limits<double>::infinity()
-
inline TrackSelector(const Config &config)
-
template<size_t M, bool ReadOnly = true>
struct TrackStateTraits - #include <Acts/EventData/MultiTrajectory.hpp>
Public Types
-
using Covariance = typename detail_lt::Types<eBoundSize, ReadOnly>::CovarianceMap
-
using Parameters = typename detail_lt::Types<eBoundSize, ReadOnly>::CoefficientsMap
-
using Projector = Eigen::Matrix<typename Covariance::Scalar, M, eBoundSize, ProjectorFlags>
Public Static Attributes
-
static constexpr auto ProjectorFlags = Eigen::RowMajor | Eigen::AutoAlign
-
using Covariance = typename detail_lt::Types<eBoundSize, ReadOnly>::CovarianceMap
-
class TrackStateType
- #include <Acts/EventData/TrackStateType.hpp>
View type over a bitset stored in a 64 bit integer This view allows modifications.
Public Types
-
using raw_type = std::uint64_t
Public Functions
-
inline TrackStateType(raw_type &raw)
Constructor from a reference to the underlying value container.
- Parameters
raw – the value container
-
inline operator ConstTrackStateType()
Automatically convert to const track state type.
-
inline TrackStateType &operator=(const ConstTrackStateType &other)
Assign the value from another set of flags.
- Parameters
other – the other set of flags to assign
- Returns
this object
-
inline TrackStateType &operator=(const TrackStateType &other)
Assign the value from another set of flags.
- Parameters
other – the other set of flags to assign
- Returns
this object
-
inline void reset(std::size_t pos)
Change the value of the bit at position at
postofalse.- Parameters
pos – the position of the bit to change
-
inline void set(std::size_t pos, bool value = true)
Change the value of the bit at position
postovalue.- Parameters
pos – the position of the bit to change
value – the value to change the bit to
-
inline bool test(std::size_t pos) const
Return if the bit at position
posis 1.- Parameters
pos – the bit position
- Returns
if the bit at
posis one or not
Public Static Attributes
-
static constexpr std::size_t kRawBits = std::numeric_limits<std::make_unsigned<raw_type>::type>::digits
-
using raw_type = std::uint64_t
-
class TrapezoidBounds : public Acts::PlanarBounds
- #include <Acts/Surfaces/TrapezoidBounds.hpp>
Bounds for a trapezoidal, planar Surface.
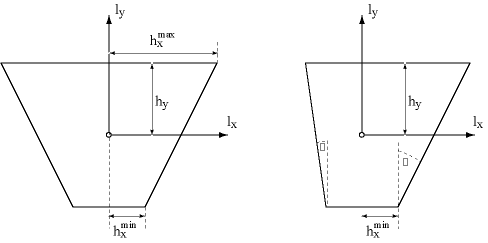
Public Types
-
enum BoundValues
Values:
-
enumerator eHalfLengthXnegY
-
enumerator eHalfLengthXposY
-
enumerator eHalfLengthY
-
enumerator eSize
-
enumerator eHalfLengthXnegY
Public Functions
-
TrapezoidBounds() = delete
-
inline TrapezoidBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor for symmetric Trapezoid - from fixed size array.
- Parameters
values – the values to be stream in
-
inline TrapezoidBounds(double halfXnegY, double halfXposY, double halfY) noexcept(false)
Constructor for symmetric Trapezoid.
- Parameters
halfXnegY – minimal half length X, definition at negative Y
halfXposY – maximal half length X, definition at positive Y
halfY – half length Y - defined at x=0
-
~TrapezoidBounds() override
-
virtual const RectangleBounds &boundingBox() const final
Bounding box parameters.
- Returns
rectangle bounds for a bounding box
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck) const final
The orientation of the Trapezoid is according to the figure above, in words: the shorter of the two parallel sides of the trapezoid intersects with the negative \( y \) - axis of the local frame.
The cases are:
(0)
\( y \) or \( x \)bounds are 0 || 0
(1) the local position is outside
\( y \)bounds
(2) the local position is inside
\( y \) bounds, but outside maximum \( x \)bounds
(3) the local position is inside
\( y \) bounds AND inside minimum \( x \)bounds
(4) the local position is inside
\( y \) bounds AND inside maximum \( x \) bounds, so that it depends on the \( eta \) coordinate (5) the local position fails test of (4)The inside check is done using single equations of straight lines and one has to take care if a point lies on the positive \( x \) half area(I) or the negative one(II). Denoting \( |x_{min}| \) and \( | x_{max} | \) as
minHalfXrespectivelymaxHalfX, such as \( | y_{H} | \) ashalfY, the equations for the straing lines in (I) and (II) can be written as:(I): \( y = \kappa_{I} x + \delta_{I} \)
(II): \( y = \kappa_{II} x + \delta_{II} \)
,
where
\( \kappa_{I} = - \kappa_{II} = 2 \frac{y_{H}}{x_{max} - x_{min}} \) and \( \delta_{I} = \delta_{II} = - \frac{1}{2}\kappa_{I}(x_{max} + x_{min}) \)
- Parameters
lposition – Local position (assumed to be in right surface frame)
bcheck – boundary check directive
- Returns
boolean indicator for the success of this operation
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
- Parameters
sl – is the ostream to be dumped into
-
virtual BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Access method for bound values, this is a dynamically sized vector containing the parameters needed to describe these bounds.
- Returns
of the stored values for this SurfaceBounds object
-
virtual std::vector<Vector2> vertices(unsigned int lseg = 1) const final
Return the vertices.
Note
the number of segments is ignored in this representation
- Parameters
lseg – the number of segments used to approximate and eventually curved line
- Returns
vector for vertices in 2D
-
enum BoundValues
-
class TrapezoidVolumeBounds : public Acts::VolumeBounds
- #include <Acts/Geometry/TrapezoidVolumeBounds.hpp>
Bounds for a trapezoidal shaped Volume, the orientedSurface(…) method creates a vector of 6 surfaces:
BoundarySurfaceFace [index]:
negativeFaceXY [0] : Trazpezoidal Acts::PlaneSurface, parallel to \( xy \) plane at negative \(z\)
positiveFaceXY [1] : Trazpezoidal Acts::PlaneSurface, parallel to \( xy \) plane at positive \(z\)
trapezoidFaceAlpha [2] : Rectangular Acts::PlaneSurface, attached to [0] and [1] at negative \(x\) (associated to alpha)
trapezoidFaceBeta [3] : Rectangular Acts::PlaneSurface, attached to [0] and [1] at positive \( x\) (associated to beta)
negativeFaceZX [4] : Rectangular Acts::PlaneSurface, parallel to \( zx \) plane at negative \(y\)
positiveFaceZX [5] : Rectangular Acts::PlaneSurface, parallel to \( zx \) plane at positive \(y\)
Public Types
-
enum BoundValues
for access / streaming
Values:
-
enumerator eHalfLengthXnegY
halflength in x at negative y
-
enumerator eHalfLengthXposY
halflength in x at positive y
-
enumerator eHalfLengthY
halflength in y
-
enumerator eHalfLengthZ
halflength in z
-
enumerator eAlpha
opening angle alpha (in point A)
-
enumerator eBeta
opening angle beta (in point B)
-
enumerator eSize
length of the bounds vector
-
enumerator eHalfLengthXnegY
Public Functions
-
TrapezoidVolumeBounds() = delete
-
inline TrapezoidVolumeBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor - from a fixed size array.
- Parameters
values – The bound values
-
TrapezoidVolumeBounds(const TrapezoidVolumeBounds &trabo) = default
-
TrapezoidVolumeBounds(double minhalex, double haley, double halez, double alpha, double beta) noexcept(false)
Constructor - the trapezoid boundaries (arbitrary trapezoid)
- Parameters
minhalex – is the half length in x at minimal y
haley – is the half length in y
halez – is the half length in z
alpha – is the opening angle at -x,-y
beta – is the opening angle at +x,-y
-
TrapezoidVolumeBounds(double minhalex, double maxhalex, double haley, double halez) noexcept(false)
Constructor - the trapezoid boundaries (symmetric trapezoid)
- Parameters
minhalex – is the half length in x at minimal y
maxhalex – is the half length in x at maximal y
haley – is the half length in y
halez – is the half length in z
-
~TrapezoidVolumeBounds() override = default
-
virtual Volume::BoundingBox boundingBox(const Transform3 *trf = nullptr, const Vector3 &envelope = {0, 0, 0}, const Volume *entity = nullptr) const final
Construct bounding box for this shape.
- Parameters
trf – Optional transform
envelope – Optional envelope to add / subtract from min/max
entity – Entity to associate this bounding box with
- Returns
Constructed bounding box
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
virtual bool inside(const Vector3 &pos, double tol = 0.) const override
This method checks if position in the 3D volume frame is inside the cylinder.
- Parameters
pos – is the global position to be checked
tol – is the tolerance applied
- Returns
boolean indicator if position is inside
-
TrapezoidVolumeBounds &operator=(const TrapezoidVolumeBounds &trabo) = default
-
virtual OrientedSurfaces orientedSurfaces(const Transform3 &transform = Transform3::Identity()) const override
Oriented surfaces, i.e.
the decomposed boundary surfaces and the according navigation direction into the volume given the normal vector on the surface
It will throw an exception if the orientation prescription is not adequate
- Parameters
transform – is the 3D transform to be applied to the boundary surfaces to position them in 3D space
- Returns
a vector of surfaces bounding this volume
-
virtual std::ostream &toStream(std::ostream &sl) const override
Output Method for std::ostream.
-
inline virtual VolumeBounds::BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Return the bound values as dynamically sized vector.
- Returns
this returns a copy of the internal values
-
template<typename external_space_point_t>
struct TripletCandidate - #include <Acts/Seeding/CandidatesForMiddleSp.hpp>
A description of a triplet candidate.
- Template Parameters
external_space_point_t – The external spacepoint type.
Public Functions
-
TripletCandidate() = default
Default Constructor.
-
TripletCandidate(const TripletCandidate&) = default
Copy operations.
-
inline TripletCandidate(external_space_point_t &b, external_space_point_t &m, external_space_point_t &t, float w, float z, bool q)
constructor
- Parameters
b – The bottom space point
m – The middle space point
t – The top space point
w – The quality of the candidate
z – The z coordinate of the origin
q – Whether the candidate is high or low quality
-
TripletCandidate(TripletCandidate&&) = default
Move operations.
-
~TripletCandidate() = default
Default Destructor.
-
TripletCandidate &operator=(const TripletCandidate&) = default
-
TripletCandidate &operator=(TripletCandidate&&) = default
Public Members
-
external_space_point_t *bottom = {nullptr}
-
bool isQuality = {false}
-
external_space_point_t *middle = {nullptr}
-
external_space_point_t *top = {nullptr}
-
float weight = {0.}
-
float zOrigin = {0.}
-
class VectorMultiTrajectory : public Acts::detail_vmt::VectorMultiTrajectoryBase, public Acts::MultiTrajectory<VectorMultiTrajectory>
- #include <Acts/EventData/VectorMultiTrajectory.hpp>
Public Functions
-
VectorMultiTrajectory() = default
-
inline VectorMultiTrajectory(const VectorMultiTrajectory &other)
-
inline VectorMultiTrajectory(VectorMultiTrajectory &&other)
-
template<typename T>
inline constexpr void addColumn_impl(const std::string &key)
-
IndexType addTrackState_impl(TrackStatePropMask mask = TrackStatePropMask::All, IndexType iprevious = kInvalid)
-
inline void allocateCalibrated_impl(IndexType istate, size_t measdim)
-
void clear_impl()
-
inline std::any component_impl(HashedString key, IndexType istate)
-
inline std::any component_impl(HashedString key, IndexType istate) const
-
inline TrackStateProxy::Covariance covariance_impl(IndexType parIdx)
-
inline ConstTrackStateProxy::Covariance covariance_impl(IndexType parIdx) const
-
inline constexpr bool has_impl(HashedString key, IndexType istate) const
-
inline constexpr bool hasColumn_impl(HashedString key) const
-
inline TrackStateProxy::Covariance jacobian_impl(IndexType istate)
-
inline ConstTrackStateProxy::Covariance jacobian_impl(IndexType istate) const
-
template<size_t measdim>
inline TrackStateProxy::Measurement<measdim> measurement_impl(IndexType istate)
-
template<size_t measdim>
inline ConstTrackStateProxy::Measurement<measdim> measurement_impl(IndexType istate) const
-
template<size_t measdim>
inline TrackStateProxy::MeasurementCovariance<measdim> measurementCovariance_impl(IndexType istate)
-
template<size_t measdim>
inline ConstTrackStateProxy::MeasurementCovariance<measdim> measurementCovariance_impl(IndexType istate) const
-
inline TrackStateProxy::Parameters parameters_impl(IndexType parIdx)
-
inline ConstTrackStateProxy::Parameters parameters_impl(IndexType parIdx) const
-
void reserve(std::size_t n)
-
inline void setUncalibratedSourceLink_impl(IndexType istate, SourceLink sourceLink)
-
inline IndexType size_impl() const
-
inline Statistics statistics() const
-
void unset_impl(TrackStatePropMask target, IndexType istate)
-
VectorMultiTrajectory() = default
-
class VectorTrackContainer : public Acts::detail_vtc::VectorTrackContainerBase
- #include <Acts/EventData/VectorTrackContainer.hpp>
Public Functions
-
inline VectorTrackContainer()
-
inline VectorTrackContainer(const ConstVectorTrackContainer &other)
-
VectorTrackContainer(const VectorTrackContainer &other) = default
-
VectorTrackContainer(VectorTrackContainer&&) = default
-
template<typename T>
inline constexpr void addColumn_impl(const std::string &key)
-
IndexType addTrack_impl()
-
void clear()
-
inline std::any component_impl(HashedString key, IndexType itrack)
-
inline std::any component_impl(HashedString key, IndexType itrack) const
-
void copyDynamicFrom_impl(IndexType dstIdx, const VectorTrackContainerBase &src, IndexType srcIdx)
-
inline Covariance covariance(IndexType itrack)
-
inline ConstCovariance covariance(IndexType itrack) const
-
void ensureDynamicColumns_impl(const detail_vtc::VectorTrackContainerBase &other)
-
inline Parameters parameters(IndexType itrack)
-
inline ConstParameters parameters(IndexType itrack) const
-
void removeTrack_impl(IndexType itrack)
-
void reserve(IndexType size)
-
inline VectorTrackContainer()
-
template<typename input_track_t>
class Vertex - #include <Acts/Vertexing/Vertex.hpp>
Class for storing vertex objects.
- Template Parameters
input_track_t – Track object type
Public Functions
-
Vertex() = default
Default constructor.
-
Vertex(const Vector3 &position)
Construct for vertex at given 3d-position, sets covariance to zero.
- Parameters
position – Vertex position
-
Vertex(const Vector3 &position, const SquareMatrix3 &covariance, const std::vector<TrackAtVertex<input_track_t>> &tracks)
Vertex constructor.
- Parameters
position – Vertex position
covariance – Position covariance matrix
tracks – Vector of tracks associated with the vertex
-
Vertex(const Vector4 &position)
Construct for vertex at given 4d-position, sets covariance to zero.
- Parameters
position – Vertex position
-
Vertex(const Vector4 &position, const SquareMatrix4 &covariance, const std::vector<TrackAtVertex<input_track_t>> &tracks)
Vertex constructor.
- Parameters
position – Full vertex position
covariance – 4x4 covariance matrix
tracks – Vector of tracks associated with the vertex
-
SquareMatrix3 covariance() const
- Returns
Returns position covariance
-
std::pair<double, double> fitQuality() const
- Returns
Returns pair of (chi2, numberDoF)
-
const SquareMatrix4 &fullCovariance() const
- Returns
Returns 4x4 covariance
-
const Vector4 &fullPosition() const
- Returns
Returns 4-position
-
Vector3 position() const
- Returns
Returns 3-position
-
void setCovariance(const SquareMatrix3 &covariance)
Sets 3x3 covariance.
- Parameters
covariance – Position covariance matrix
-
void setFitQuality(double chiSquared, double numberDoF)
- Parameters
chiSquared – Chi2 of fit
numberDoF – Number of degrees of freedom
-
void setFitQuality(std::pair<double, double> fitQuality)
- Parameters
fitQuality – pair of (chi2, numberDoF)
-
void setFullCovariance(const SquareMatrix4 &covariance)
Sets 4x4 covariance.
- Parameters
covariance – The 4x4 covariance matrix
-
void setFullPosition(const Vector4 &fullPosition)
Set position and time.
- Parameters
fullPosition – Vertex position and time
-
void setPosition(const Vector3 &position, ActsScalar time = 0)
Set position and time.
- Parameters
position – Vertex position
time – The time
-
void setTime(ActsScalar time)
Sets time.
- Parameters
time – The time
-
void setTracksAtVertex(const std::vector<TrackAtVertex<input_track_t>> &tracks)
- Parameters
tracks – Vector of tracks at vertex
-
ActsScalar time() const
- Returns
Returns time
-
const std::vector<TrackAtVertex<input_track_t>> &tracks() const
- Returns
Returns vector of tracks associated with the vertex
-
template<typename input_track_t>
struct VertexInfo - #include <Acts/Vertexing/AMVFInfo.hpp>
Helper struct for storing vertex related information.
Public Functions
-
VertexInfo() = default
-
inline VertexInfo(const Acts::Vertex<input_track_t> &vtx, const Acts::Vector4 &pos)
Public Members
-
Acts::Vertex<input_track_t> constraintVertex
-
std::map<const input_track_t*, const BoundTrackParameters> ip3dParams
-
bool relinearize = true
-
std::vector<const input_track_t*> trackLinks
-
VertexInfo() = default
-
template<typename input_track_t>
struct VertexingOptions - #include <Acts/Vertexing/VertexingOptions.hpp>
Vertex Finder Options.
Public Functions
-
VertexingOptions() = delete
Default constructor is deleted.
-
inline VertexingOptions(const GeometryContext &gctx, const MagneticFieldContext &mctx)
VertexingOptions with context and without vertex constraint.
- Parameters
gctx – Geometry context
mctx – Magnetic field context
-
inline VertexingOptions(const GeometryContext &gctx, const MagneticFieldContext &mctx, const Vertex<input_track_t> &constr, const bool useConstr = true)
VertexingOptions with context and vertex constraint.
- Parameters
gctx – Geometry context
mctx – Magnetic field context
constr – Vertex constraint
useConstr – Boolean indicating whether vertex constraint should be used during the vertex fit
Public Members
-
Vertex<input_track_t> constraint
Vertex constraint.
Important note: While this variable is not used during the vertex fit if useConstraintInFit is set to false, it is always used during vertex finding.
-
std::reference_wrapper<const GeometryContext> geoContext
Context object for the geometry.
-
std::reference_wrapper<const MagneticFieldContext> magFieldContext
Context object for the magnetic field.
-
bool useConstraintInFit
Boolean indicating whether we use the constraint information during the vertex fit.
If set to true, the covariance matrix of constraint must be invertible.
-
VertexingOptions() = delete
-
struct ViewConfig
- #include <Acts/Visualization/ViewConfig.hpp>
Struct to concentrate all visualization configurations in order to harmonize visualization interfaces.
Public Functions
-
inline ViewConfig(bool vis = true)
Constructor to switch visibility off.
-
inline ViewConfig(const ColorRGB &rgb)
Constructor for color settings only.
Public Members
-
ColorRGB color = {250, 0, 0}
The RGB color for this object.
-
double lineThickness = 0.15
The visual line thickness for this object.
-
unsigned int nSegments = 72
The number of segments to approximate full 2pi.
-
double offset = 0.1
Out of plane drawing parameter for objects.
-
std::string outputName = ""
Write name - non-empty string indicates writing.
-
double surfaceThickness = 0.15
The visual surface thickness for this object.
-
bool triangulate = false
Whether to triangulate or not.
-
bool visible = true
Visible flag.
-
inline ViewConfig(bool vis = true)
-
class Volume : public virtual Acts::GeometryObject
- #include <Acts/Geometry/Volume.hpp>
It inhertis of GeometryObject for TDD identification.
Base class for all volumes inside the tracking realm, it defines the interface for inherited Volume classes regarding the geometrical information.
Subclassed by Acts::AbstractVolume, Acts::TrackingVolume
Public Types
-
using BoundingBox = AxisAlignedBoundingBox<Volume, ActsScalar, 3>
Public Functions
-
Volume() = delete
-
Volume(const Transform3 &transform, VolumeBoundsPtr volbounds)
Explicit constructor with shared arguments.
Note
This will automatically build an oriented bounding box with an envelope value of (0.05, 0.05, 0.05)mm
- Parameters
transform – is the transform to position the volume in 3D space
volbounds – is the volume boundary definitions
-
Volume(const Volume &vol, const Transform3 &shift = Transform3::Identity())
Copy Constructor - with optional shift.
Note
This will automatically build an oriented bounding box with an envelope value of (0.05, 0.05, 0.05)mm
- Parameters
vol – is the source volume for the copy
shift – is the optional shift applied as : shift * vol.transform()
-
virtual ~Volume() = default
-
virtual Vector3 binningPosition(const GeometryContext &gctx, BinningValue bValue) const override
The binning position method.
as default the center is given, but may be overloaded
- Parameters
gctx – The current geometry context object, e.g. alignment
bValue – is the binning value schema
- Returns
vector 3D that can be used for the binning
-
BoundingBox boundingBox(const Vector3 &envelope = {0, 0, 0}) const
Construct bounding box for this shape.
- Parameters
envelope – Optional envelope to add / subtract from min/max
- Returns
Constructed bounding box pointing to this volume
-
inline const Vector3 ¢er() const
returns the center of the volume
-
bool inside(const Vector3 &gpos, double tol = 0.) const
Inside() method for checks.
- Parameters
gpos – is the position to be checked
tol – is the tolerance parameter
- Returns
boolean indicator if the position is inside
-
inline const Transform3 &itransform() const
Returns the inverted transform of this volume.
-
Volume &operator=(const Volume &vol)
Assignment operator.
- Parameters
vol – is the source volume to be copied
-
const BoundingBox &orientedBoundingBox() const
Construct oriented bounding box for this shape.
- Returns
Constructed oriented bounding box pointing to this volume
-
inline const Transform3 &transform() const
Return methods for geometry transform.
-
inline const VolumeBounds &volumeBounds() const
returns the volumeBounds()
-
using BoundingBox = AxisAlignedBoundingBox<Volume, ActsScalar, 3>
-
class VolumeBounds
- #include <Acts/Geometry/VolumeBounds.hpp>
Pure Absract Base Class for Volume bounds.
Acts::VolumeBounds are a set of up to six confining Surfaces that are stored in a std::vector. Each type of Acts::VolumeBounds has to implement a orientedSurfaces() and a inside() method.
The Volume, retrieving a set of Surfaces from the VolumeBounds, can turn the Surfaces into BoundarySurfaces.
Subclassed by Acts::ConeVolumeBounds, Acts::CuboidVolumeBounds, Acts::CutoutCylinderVolumeBounds, Acts::CylinderVolumeBounds, Acts::GenericCuboidVolumeBounds, Acts::TrapezoidVolumeBounds
Public Types
-
enum BoundsType
This is nested to the VolumeBounds, as also SurfaceBounds will have Bounds Type.
Values:
-
enumerator eCone
-
enumerator eCuboid
-
enumerator eCutoutCylinder
-
enumerator eCylinder
-
enumerator eGenericCuboid
-
enumerator eTrapezoid
-
enumerator eOther
-
enumerator eCone
Public Functions
-
VolumeBounds() = default
-
virtual ~VolumeBounds() = default
-
inline virtual double binningBorder(BinningValue bValue) const
Binning borders in double.
- Parameters
bValue – is the binning schema used
- Returns
float offset to be used for the binning
-
inline virtual Vector3 binningOffset(BinningValue bValue) const
Binning offset - overloaded for some R-binning types.
- Parameters
bValue – is the binning schema used
- Returns
vector 3D to be used for the binning
-
virtual Volume::BoundingBox boundingBox(const Transform3 *trf = nullptr, const Vector3 &envelope = {0, 0, 0}, const Volume *entity = nullptr) const = 0
Construct bounding box for this shape.
- Parameters
trf – Optional transform
envelope – Optional envelope to add / subtract from min/max
entity – Entity to associate this bounding box with
- Returns
Constructed bounding box
-
virtual bool inside(const Vector3 &gpos, double tol = 0.) const = 0
Checking if position given in volume frame is inside.
- Parameters
gpos – is the global position to be checked
tol – is the tolerance applied for the inside check
- Returns
boolean indicating if the position is inside
-
virtual OrientedSurfaces orientedSurfaces(const Transform3 &transform = Transform3::Identity()) const = 0
Oriented surfaces, i.e.
the decomposed boundary surfaces and the according navigation direction into the volume given the normal vector on the surface
It will throw an exception if the orientation prescription is not adequate
- Parameters
transform – is the 3D transform to be applied to the boundary surfaces to position them in 3D space
- Returns
a vector of surfaces bounding this volume
-
virtual std::ostream &toStream(std::ostream &sl) const = 0
Output Method for std::ostream, to be overloaded by child classes.
- Parameters
sl – is the output stream to be dumped into
-
virtual BoundsType type() const = 0
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
virtual std::vector<double> values() const = 0
Access method for bound values, this is a dynamically sized vector containing the parameters needed to describe these bounds.
- Returns
of the stored values for this SurfaceBounds object
-
enum BoundsType
-
template<typename Selector = VolumeSelector>
struct VolumeCollector - #include <Acts/Propagator/VolumeCollector.hpp>
A Volume Collector struct templated with a Selector type.
Whenever a volume is passed in the propagation that satisfies the selector, it is recorded for further usage in the flow.
Public Types
-
using result_type = this_result
Public Functions
Collector action for the ActionList of the Propagator It checks if the propagator state has a current volume, in which case the action is performed:
it records the volume given the configuration
- Template Parameters
propagator_state_t – is the type of Propagator state
stepper_t – Type of the stepper used for the propagation
navigator_t – Type of the navigator used for the propagation
- Parameters
state – [inout] is the mutable stepper state object
stepper – [in] The stepper in use
navigator – [in] The navigator in use
result – [inout] is the mutable result object
logger – the logger object
Public Members
-
Selector selector
The selector used for this volume.
-
struct this_result
- #include <Acts/Propagator/VolumeCollector.hpp>
Simple result struct to be returned It has all the VolumeHit objects that are collected (and thus have been selected)
Public Members
-
std::vector<VolumeHit> collected
-
std::vector<VolumeHit> collected
-
using result_type = this_result
-
struct VolumeConfig
- #include <Acts/Geometry/CylinderVolumeBuilder.hpp>
VolumeConfig struct to understand the layer config.
Public Functions
-
inline VolumeConfig()
Default constructor.
-
inline void adapt(const VolumeConfig &lConfig)
Adapt to the dimensions of another config it will take the maximum/minimum values and just overwrite them.
- Parameters
lConfig – [in] is the config to which it should be adapded
-
inline void adaptR(const VolumeConfig &lConfig)
Adapt to the dimensions of another config in R it will take the maximum/minimum values and just overwrite them.
- Parameters
lConfig – [in] is the config to which it should be adapded
-
inline void adaptZ(const VolumeConfig &lConfig)
Adapt to the dimensions of another config in Z it will take the maximum/minimum values and just overwrite them.
- Parameters
lConfig – [in] is the config to which it should be adapded
-
inline void attachZ(const VolumeConfig &lConfig)
Attach method - const it attaches the one volume config to the other one.
- Parameters
lConfig – [in] is the confit to which it should be attached
-
inline bool contains(const VolumeConfig &vConfig) const
Check if contained full set.
- Parameters
vConfig – [in] is the config against which is checked
-
inline bool containsInR(const VolumeConfig &vConfig) const
Check if contained radially.
- Parameters
vConfig – [in] is the config against which is checked
-
inline bool containsInZ(const VolumeConfig &vConfig) const
Check if contained longitudinally.
- Parameters
vConfig – [in] is the config against which is checked
-
inline void midPointAttachZ(VolumeConfig &lConfig)
Attach method - non-const it attaches the one volume config to the other one in Z this is the non-cost method, i.e.
the mid point is used
Note
lConfig will be changed
- Parameters
lConfig – [in] is the config to which it should be attached
-
inline operator bool() const
Conversion operator to bool.
-
inline bool overlapsInR(const VolumeConfig &vConfig) const
Overlap check radially.
- Parameters
vConfig – [in] is the config against which is checked
- Returns
boolean if the overlap in r exists
-
inline bool overlapsInZ(const VolumeConfig &vConfig) const
Overlap check longitudinally.
- Parameters
vConfig – [in] is the config against which is checked
- Returns
boolean if the overlap in z exists
-
inline std::string toString() const
Method for output formatting.
-
inline bool wraps(const VolumeConfig &vConfig) const
Compatibility check full set.
- Parameters
vConfig – [in] is the config against which is checked
- Returns
boolean if the current volume wraps the vConfig fully
Public Members
-
LayerVector layers
the layers you have
-
bool present = {false}
layers are present
-
double rMax
max parameter r
-
double rMin
min parameter r
-
MutableTrackingVolumeVector volumes
the confined volumes you have
-
bool wrapping = {false}
in what way they are binned
-
double zMax
max parameter z
-
double zMin
min parameter z
-
inline VolumeConfig()
-
struct VolumeHit
- #include <Acts/Propagator/VolumeCollector.hpp>
The information to be writtern out per hit volume.
-
class VolumeMaterialMapper
- #include <Acts/Material/VolumeMaterialMapper.hpp>
VolumeMaterialMapper.
This is the main feature tool to map material information from a 3D geometry onto the TrackingGeometry with its surface material description.
The process runs as such:
1) TrackingGeometry is parsed and for each Volume with ProtoVolumeMaterial a local store is initialized the identification is done hereby through the Volume::GeometryIdentifier
2) A number of N material tracks is read in, each track has : origin, direction, material steps (< position, step length, x0, l0, a, z, rho >, thichness)
for each track: volume along the origin/direction path are collected. the step are then associated to volume inside which they are. Additional step are created along the track direction.
3) Each ‘hit’ bin per event is counted and averaged at the end of the run
Public Types
-
using StraightLinePropagator = Propagator<StraightLineStepper, Navigator>
Public Functions
-
VolumeMaterialMapper() = delete
Delete the Default constructor.
-
VolumeMaterialMapper(const Config &cfg, StraightLinePropagator propagator, std::unique_ptr<const Logger> slogger = getDefaultLogger("VolumeMaterialMapper", Logging::INFO))
Constructor with config object.
- Parameters
cfg – Configuration struct
propagator – The straight line propagator
slogger – The logger
-
State createState(const GeometryContext &gctx, const MagneticFieldContext &mctx, const TrackingGeometry &tGeometry) const
helper method that creates the cache for the mapping
This method takes a TrackingGeometry, finds all surfaces with material proxis and returns you a Cache object tO be used
- Parameters
gctx – [in] The geometry context to use
mctx – [in] The magnetic field context to use
tGeometry – [in] The geometry which should be mapped
-
void finalizeMaps(State &mState) const
Method to finalize the maps.
It calls the final run averaging and then transforms the Homogeneous material into HomogeneousVolumeMaterial and the 2D and 3D grid into a InterpolatedMaterialMap
- Parameters
mState –
-
void mapMaterialTrack(State &mState, RecordedMaterialTrack &mTrack) const
Process/map a single track.
Note
the RecordedMaterialSlab of the track are assumed to be ordered from the starting position along the starting direction
- Parameters
mState – The current state map
mTrack – The material track to be mapped
-
struct Config
- #include <Acts/Material/VolumeMaterialMapper.hpp>
Nested Configuration struct for the material mapper.
Public Members
-
float mappingStep = 1.
Size of the step for the step extrapolation.
-
float mappingStep = 1.
-
struct State
- #include <Acts/Material/VolumeMaterialMapper.hpp>
Nested State struct which is used for the mapping prococess.
Public Functions
-
inline State(const GeometryContext &gctx, const MagneticFieldContext &mctx)
Constructor of the State with contexts.
Public Members
-
std::reference_wrapper<const GeometryContext> geoContext
Reference to the geometry context for the mapping.
-
std::map<const GeometryIdentifier, Grid2D> grid2D
The 2D material grid for each geometry ID.
-
std::map<const GeometryIdentifier, Grid3D> grid3D
The 3D material grid for each geometry ID.
-
std::map<const GeometryIdentifier, Acts::AccumulatedVolumeMaterial> homogeneousGrid
The recorded material per geometry ID.
-
std::reference_wrapper<const MagneticFieldContext> magFieldContext
Reference to the magnetic field context.
-
std::map<const GeometryIdentifier, BinUtility> materialBin
The binning for each geometry ID.
-
std::map<GeometryIdentifier, std::shared_ptr<const ISurfaceMaterial>> surfaceMaterial
The surface material of the input tracking geometry.
-
std::map<const GeometryIdentifier, std::function<Acts::Vector2(Acts::Vector3)>> transform2D
The recorded 2D transform associated the grid for each geometry ID.
-
std::map<const GeometryIdentifier, std::function<Acts::Vector3(Acts::Vector3)>> transform3D
The recorded 3D transform associated the material grid for each geometry ID.
-
std::map<GeometryIdentifier, std::unique_ptr<const IVolumeMaterial>> volumeMaterial
The created volume material from it.
-
inline State(const GeometryContext &gctx, const MagneticFieldContext &mctx)
-
using StraightLinePropagator = Propagator<StraightLineStepper, Navigator>
-
struct VolumeSelector
- #include <Acts/Propagator/VolumeCollector.hpp>
Simple struct to select volumes.
Public Functions
-
inline VolumeSelector(bool sMaterial = true, bool sLayer = false, bool sPassive = false)
VolumeSelector with options.
- Parameters
sMaterial – is the directive to select material volumes
sLayer – is the directive to select volumes with layers
sPassive – is the directive to select passive volumes
-
inline bool operator()(const Acts::TrackingVolume &volume) const
Call operator to check if a volume should be selected.
- Parameters
volume – is the test volume
Public Members
-
bool selectLayer = false
-
bool selectMaterial = true
-
bool selectPassive = false
-
inline VolumeSelector(bool sMaterial = true, bool sLayer = false, bool sPassive = false)
-
struct WeightedComponentReducerLoop
- #include <Acts/Propagator/MultiEigenStepperLoop.hpp>
Reducer struct for the Loop MultiEigenStepper which reduces the multicomponent state to simply by summing the weighted values.
Public Static Functions
-
template<typename stepper_state_t>
static inline ActsScalar absoluteMomentum(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline ActsScalar charge(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline FreeVector cov(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline Vector3 direction(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline Vector3 momentum(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline FreeVector pars(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline Vector3 position(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline ActsScalar qOverP(const stepper_state_t &s)
-
template<typename stepper_state_t>
static inline ActsScalar time(const stepper_state_t &s)
-
template<typename component_range_t>
static inline Vector3 toVector3(const component_range_t &comps, const FreeIndices i)
-
template<typename stepper_state_t>
-
struct WrappingConfig
- #include <Acts/Geometry/CylinderVolumeBuilder.hpp>
The WrappingSetup that is happening here.
Public Functions
-
WrappingConfig() = default
constructor
-
inline void configureContainerVolume()
configure the new Volume
-
inline std::string toString() const
Method for output formatting.
-
inline void wrapInsertAttach()
wrap, insert, attach
Public Members
-
VolumeConfig containerVolumeConfig
the combined volume
-
VolumeConfig cVolumeConfig
-
VolumeConfig existingVolumeConfig
existing volume config with potential gaps
-
VolumeConfig externalVolumeConfig
externally provided config, this can only change the the ncp volumes
-
VolumeConfig fGapVolumeConfig
-
VolumeConfig nVolumeConfig
the new volumes
-
VolumeConfig pVolumeConfig
-
VolumeConfig sGapVolumeConfig
-
WrappingCondition wCondition = Undefined
-
std::string wConditionScreen = "[left untouched]"
-
WrappingConfig() = default
-
template<typename vfitter_t>
class ZScanVertexFinder - #include <Acts/Vertexing/ZScanVertexFinder.hpp>
Implements a vertex finder based on the mode of z0 values:
Determines the mode value of all input track z0 values
If no constraint is given, returns (0,0, z0_mode) as vertex position
If vertex constraint is given with x=x_constr and y=y_constr, the returned vertex position will be (x_constr, y_constr, z0_mode).
Public Types
-
using InputTrack_t = typename vfitter_t::InputTrack_t
Public Functions
-
inline ZScanVertexFinder(const Config &cfg, std::function<BoundTrackParameters(InputTrack_t)> func, std::unique_ptr<const Logger> logger = getDefaultLogger("ZScanVertexFinder", Logging::INFO))
Constructor for user-defined InputTrack_t type =! BoundTrackParameters.
- Parameters
cfg – Configuration object
func – Function extracting BoundTrackParameters from InputTrack_t object
logger – Logging instance
-
template<typename T = InputTrack_t, std::enable_if_t<std::is_same<T, BoundTrackParameters>::value, int> = 0>
inline ZScanVertexFinder(const Config &cfg, std::unique_ptr<const Logger> logger = getDefaultLogger("ZScanVertexFinder", Logging::INFO)) Constructor used if InputTrack_t type == BoundTrackParameters.
- Parameters
cfg – Configuration object
logger – The logging instance
-
Result<std::vector<Vertex<InputTrack_t>>> find(const std::vector<const InputTrack_t*> &trackVector, const VertexingOptions<InputTrack_t> &vertexingOptions, State &state) const
Function that determines single vertex, based on z0 values of input tracks, using a Half Sample Mode algorithm.
- Parameters
trackVector – Input track collection
vertexingOptions – Vertexing options
state – State for fulfilling correct interface
- Returns
Vector of vertices, filled with a single vertex (for consistent interfaces)
-
struct Config
- #include <Acts/Vertexing/ZScanVertexFinder.hpp>
Configuration struct.
Public Functions
-
inline Config(const ImpactPointEstimator<InputTrack_t, Propagator_t> &ipEst)
Finder configuration.
- Parameters
ipEst – ImpactPointEstimator
Public Members
-
float constraintcutoff = 9.
-
float constrainttemp = 1.
-
bool disableAllWeights = false
-
double expPt = 1.
-
ImpactPointEstimator<InputTrack_t, Propagator_t> ipEstimator
-
double minPt = 0.4 * UnitConstants::GeV
-
double minWeight = 0.01
-
FsmwMode1dFinder mode1dFinder
-
bool useLogPt = true
-
bool usePt = false
-
inline Config(const ImpactPointEstimator<InputTrack_t, Propagator_t> &ipEst)
-
struct State
- #include <Acts/Vertexing/ZScanVertexFinder.hpp>
State struct for fulfilling interface.
-
namespace AxisJsonConverter
Functions
-
nlohmann::json toJson(const IAxis &ia)
Convert an axis to json.
- Parameters
ia – the axis
- Returns
a json object to represent the axis
-
nlohmann::json toJson(const IAxis &ia)
-
namespace Ccl
Typedefs
-
using Label = int
Enums
-
enum class ConnectResult
Values:
-
enumerator eNoConn
-
enumerator eNoConnStop
-
enumerator eConn
-
enumerator eNoConn
Functions
-
template<typename CellCollection, typename ClusterCollection, size_t GridDim = 2, typename Connect = DefaultConnect<typename CellCollection::value_type, GridDim>>
ClusterCollection createClusters(CellCollection &cells, Connect connect = Connect()) createClusters Convenience function which runs both labelClusters and createClusters.
-
template<typename CellCollection, size_t GridDim = 2, typename Connect = DefaultConnect<typename CellCollection::value_type, GridDim>>
void labelClusters(CellCollection &cells, Connect connect = Connect()) labelClusters
In-place connected component labelling using the Hoshen-Kopelman algorithm. The
Celltype must have the following functions defined: int getCellRow(const Cell&), int getCellColumn(const Cell&) int& getCellLabel(Cell&)- Parameters
cells – [in] the cell collection to be labeled
connect – [in] the connection type (see DefaultConnect)
-
template<typename CellCollection, typename ClusterCollection, size_t GridDim>
ClusterCollection mergeClusters(CellCollection&) mergeClusters
Merge a set of cells previously labeled (for instance with
labelClusters) into actual clusters. The Cluster type must have the following function defined: void clusterAddCell(Cluster&, const Cell&)- Returns
nothing
Variables
-
constexpr Label NO_LABEL = 0
-
template<typename Cell>
struct Connect1D - #include <Acts/Clusterization/Clusterization.hpp>
Subclassed by Acts::Ccl::DefaultConnect< Cell, 1 >
Public Functions
-
ConnectResult operator()(const Cell &ref, const Cell &iter) const
-
ConnectResult operator()(const Cell &ref, const Cell &iter) const
-
template<typename Cell>
struct Connect2D - #include <Acts/Clusterization/Clusterization.hpp>
Subclassed by Acts::Ccl::DefaultConnect< Cell, 2 >
Public Functions
-
inline Connect2D()
-
inline explicit Connect2D(bool commonCorner)
-
ConnectResult operator()(const Cell &ref, const Cell &iter) const
Public Members
-
bool conn8
-
inline Connect2D()
-
template<typename Cell, size_t GridDim = 2>
struct DefaultConnect - #include <Acts/Clusterization/Clusterization.hpp>
-
using Label = int
-
namespace Concepts
Typedefs
-
template<class Default, template<class...> class Op, class ...Args>
using detected_or = detail::detector<Default, void, Op, Args...> Helper which invokes the detector with a default type, and resolves to the type.
- Template Parameters
Default – The type to resolve to if
Op<Args...>does not resolve.Op – The operation
Args – The argument to the operation
-
template<template<class...> class Op, class ...Args>
using detected_t = typename detail::detector<detail::nonesuch, void, Op, Args...>::type This type calls into the detector (same as
is_detected) but it extracts the return type ofOp<Args...>.- Template Parameters
Op – The operation
Args – The arguments to the operation
-
template<template<class...> class Op, class ...Args>
using is_detected = typename detail::detector<detail::nonesuch, void, Op, Args...>::value_t This type ties together the detection idiom.
It instantiates the
detectortemplate with theOpandArgsand resolves to the exact value type. In essence, ifOp<Args...>succeeds, this will evaluate tostd::true_type, and if not, it will evaluate tostd::false_type.- Template Parameters
Op – The operation to test
Args – The arguments to the operation
-
template<class To, template<class...> class Op, class ...Args>
using is_detected_convertible = std::is_convertible<detected_t<Op, Args...>, To> This evaluates
Opinside the detector, and checks whether the resolved type is convertible toTo.- Template Parameters
To – The type to check convertibility to.
Op – The operation
Args – The arguments to the operation
-
template<class Expected, template<class...> class Op, class ...Args>
using is_detected_exact = std::is_same<Expected, detected_t<Op, Args...>> This invokes
detected_t, and checks whether its result matchesExpected.- Template Parameters
Expected – The expected result of the operation.
Op – The operation
Args – The arguments to the operation
-
template<typename T>
using ReturnTypeAbsoluteMomentum = decltype(std::declval<T>().absoluteMomentum())
-
template<typename T>
using ReturnTypeCharge = decltype(std::declval<T>().charge())
-
template<typename T>
using ReturnTypeCovariance = decltype(std::declval<T>().covariance())
-
template<typename T>
using ReturnTypeDirection = decltype(std::declval<T>().direction())
-
template<typename T>
using ReturnTypeFourPosition = decltype(std::declval<T>().fourPosition())
-
template<typename T>
using ReturnTypeFourPositionFromContext = decltype(std::declval<T>().fourPosition(std::declval<GeometryContext>()))
-
template<typename T>
using ReturnTypeParameters = decltype(std::declval<T>().parameters())
-
template<typename T>
using ReturnTypePosition = decltype(std::declval<T>().position())
-
template<typename T>
using ReturnTypePositionFromContext = decltype(std::declval<T>().position(std::declval<GeometryContext>()))
-
template<typename T>
using ReturnTypeReferenceSurface = decltype(std::declval<T>().referenceSurface())
-
template<typename T>
using ReturnTypeTime = decltype(std::declval<T>().time())
-
template<typename T>
using TypeCovarianceMatrix = typename T::CovarianceMatrix
-
template<typename T>
using TypeParametersVector = typename T::ParametersVector
-
template<typename T>
using TypeScalar = typename T::Scalar
Variables
-
template<typename parameters_t>
constexpr bool BoundTrackParametersConcept = BoundTrackParametersConceptImpl<parameters_t>::value
-
template<class To, template<class...> class Op, class ...Args>
constexpr bool converts_to = is_detected_convertible<To, Op, Args...>::value Alias to conversion check, which also extracts the constexpr boolean value.
- Template Parameters
To – The type to check convertibility to.
Op – The operation
Args – The arguments to the operation.
-
template<bool... Bs>
constexpr bool disallow = not require<Bs...> Alias for the negation of a
require.This is essentially a NOT ANY test.
- Template Parameters
Bs – The booleans.
-
template<bool... Bs>
constexpr bool either = std::disjunction<std::bool_constant<Bs>...>::value Helper which forms the logical OR of its arguments.
Converts to
std::bool_constant.- Template Parameters
Bs – The booleans to combine.
-
template<template<class...> class Op, class ...Args>
constexpr bool exists = is_detected<Op, Args...>::value Alias to
is_detectedwhich unpacks the constexpr boolean value.- Template Parameters
Op – The operation
Args – The arguments to the operation.
-
template<typename parameters_t>
constexpr bool FreeTrackParametersConcept = FreeTrackParametersConceptImpl<parameters_t>::value
-
template<typename T, template<class...> class M, typename V>
constexpr bool has_member = identical_to<V, M, T> Helper to assert if a member of a given type exists.
Basically only calls into
identical_tobut is nicer to read.- Template Parameters
T – The type to check existence of member on.
M – The member type trait
V – The type that the member is supposed to have.
-
template<typename T, typename R, template<class...> class M, typename ...Arguments>
constexpr bool has_method = M<T, R, Arguments...>::template tv<T>::value Helper which evaluates whether the type
Thas a method with a given signature.- Template Parameters
T – The type to check on. This can contain a const qualifier if you want to check on that.
R – The return type
M – The method trait, as generated by METHOD_TRAIT
Arguments – The argument types that make up the signature.
-
template<class Exact, template<class...> class Op, class ...Args>
constexpr bool identical_to = is_detected_exact<Exact, Op, Args...>::value Unpacks the constexpr boolean value from
is_detected_exact- Template Parameters
Exact – The type to check identity against
Op – The operation
Args – The arguments to the operation.
-
template<bool... Bs>
constexpr bool require = std::conjunction<std::bool_constant<Bs>...>::value Define some sort of “Domain Specific Language” to declare concepts a little more naturally.
These are taken from https://izzys.casa/2016/09/implementing-concepts-in-cxx/ Helper which combines a set of predicates (constexpr bools) with a logical AND. Converts to
std::bool_constant.- Template Parameters
Bs – The booleans to combine
-
template<typename T>
struct BoundTrackParametersConceptImpl - #include <Acts/EventData/TrackParametersConcept.hpp>
Public Static Attributes
-
static constexpr bool hasMethodAbsoluteMomentum = identical_to<TypeScalar<T>, ReturnTypeAbsoluteMomentum, const T>
-
static constexpr bool hasMethodCharge = identical_to<TypeScalar<T>, ReturnTypeCharge, const T>
-
static constexpr bool hasMethodCovariance = std::is_convertible_v<ReturnTypeCovariance<T>, std::optional<BoundSquareMatrix>>
-
static constexpr bool hasMethodDirection = identical_to<Vector3, ReturnTypeDirection, const T>
-
static constexpr bool hasMethodFourPositionFromContext = identical_to<Vector4, ReturnTypeFourPositionFromContext, const T>
-
static constexpr bool hasMethodParameters = std::is_convertible_v<ReturnTypeParameters<T>, BoundVector>
-
static constexpr bool hasMethodPositionFromContext = identical_to<Vector3, ReturnTypePositionFromContext, const T>
-
static constexpr bool hasMethodReferenceSurface = identical_to<const Surface&, ReturnTypeReferenceSurface, const T>
-
static constexpr bool hasMethodTime = identical_to<TypeScalar<T>, ReturnTypeTime, const T>
-
static constexpr bool hasTypeCovarianceMatrix = exists<TypeCovarianceMatrix, const T>
-
static constexpr bool hasTypeParametersVector = exists<TypeParametersVector, const T>
-
static constexpr bool hasTypeScalar = exists<TypeScalar, const T>
-
static constexpr bool value = require<hasTypeScalar, hasTypeParametersVector, hasTypeCovarianceMatrix, hasMethodParameters, hasMethodCovariance, hasMethodFourPositionFromContext, hasMethodPositionFromContext, hasMethodTime, hasMethodDirection, hasMethodAbsoluteMomentum, hasMethodCharge, hasMethodReferenceSurface>
-
static constexpr bool hasMethodAbsoluteMomentum = identical_to<TypeScalar<T>, ReturnTypeAbsoluteMomentum, const T>
-
template<typename T>
struct FreeTrackParametersConceptImpl - #include <Acts/EventData/TrackParametersConcept.hpp>
Public Static Attributes
-
static constexpr bool hasMethodAbsoluteMomentum = identical_to<TypeScalar<T>, ReturnTypeAbsoluteMomentum, const T>
-
static constexpr bool hasMethodCharge = identical_to<TypeScalar<T>, ReturnTypeCharge, const T>
-
static constexpr bool hasMethodCovariance = std::is_convertible_v<ReturnTypeCovariance<T>, std::optional<FreeSquareMatrix>>
-
static constexpr bool hasMethodDirection = identical_to<Vector3, ReturnTypeDirection, const T>
-
static constexpr bool hasMethodFourPosition = identical_to<Vector4, ReturnTypeFourPosition, const T>
-
static constexpr bool hasMethodParameters = std::is_convertible_v<ReturnTypeParameters<T>, FreeVector>
-
static constexpr bool hasMethodPosition = identical_to<Vector3, ReturnTypePosition, const T>
-
static constexpr bool hasMethodTime = identical_to<TypeScalar<T>, ReturnTypeTime, const T>
-
static constexpr bool hasTypeCovarianceMatrix = exists<TypeCovarianceMatrix, const T>
-
static constexpr bool hasTypeParametersVector = exists<TypeParametersVector, const T>
-
static constexpr bool hasTypeScalar = exists<TypeScalar, const T>
-
static constexpr bool hasMethodAbsoluteMomentum = identical_to<TypeScalar<T>, ReturnTypeAbsoluteMomentum, const T>
-
namespace Linearizer
Typedefs
-
template<typename T>
using propagator_t = typename T::Propagator_t
-
template<typename T>
using state_t = typename T::State
Functions
-
METHOD_TRAIT(linTrack_t, linearizeTrack)
-
template<typename S>
struct LinearizerConcept - #include <Acts/Vertexing/LinearizerConcept.hpp>
Public Static Attributes
-
static constexpr bool linTrack_exists = has_method<const S, Result<LinearizedTrack>, linTrack_t, constBoundTrackParameters&, constVector4&, constActs::GeometryContext&, constActs::MagneticFieldContext&, typename S::State&>
-
static constexpr bool propagator_exists = exists<propagator_t, S>
-
static constexpr bool value = require<linTrack_exists, propagator_exists, state_exists>
-
static constexpr bool linTrack_exists = has_method<const S, Result<LinearizedTrack>, linTrack_t, constBoundTrackParameters&, constVector4&, constActs::GeometryContext&, constActs::MagneticFieldContext&, typename S::State&>
-
template<typename T>
-
namespace SourceLinkAccessor
Typedefs
-
template<typename T>
using container_t = typename T::Container
-
template<typename T>
using iterator_t = typename T::Iterator
-
template<typename T>
using key_t = typename T::Key
-
template<typename T>
using value_t = typename T::Value
Functions
-
METHOD_TRAIT(at_t, at)
-
METHOD_TRAIT(count_t, count)
-
METHOD_TRAIT(range_t, range)
-
template<typename S>
struct SourceLinkAccessorConcept - #include <Acts/TrackFinding/SourceLinkAccessorConcept.hpp>
Public Static Attributes
-
static constexpr bool at_exists = has_method<const S, const typename S::Value&, at_t, const typename S::Iterator&>
-
static constexpr bool container_exists = exists<container_t, S>
-
static constexpr bool container_pointer_exists = std::is_same_v<std::decay_t<decltype(*(std::declval<S>().container))>, container_t<S>>
-
static constexpr bool count_exists = has_method<const S, size_t, count_t, constSurface&>
-
static constexpr bool iterator_exists = exists<iterator_t, S>
-
static constexpr bool range_exists = has_method<const S, std::pair<typename S::Iterator, typename S::Iterator>, range_t, constSurface&>
-
static constexpr bool value = require<container_exists, key_exists, value_exists, container_pointer_exists, iterator_exists, count_exists, range_exists, at_exists>
-
static constexpr bool at_exists = has_method<const S, const typename S::Value&, at_t, const typename S::Iterator&>
-
template<typename T>
-
namespace Stepper
Typedefs
-
template<typename T>
using bound_state_t = typename T::BoundState
-
template<typename T>
using cov_t = decltype(std::declval<T>().cov)
-
template<typename T>
using cov_transport_t = decltype(std::declval<T>().covTransport)
-
template<typename T>
using covariance_t = typename T::Covariance
-
template<typename T>
using curvilinear_state_t = typename T::CurvilinearState
-
template<typename T>
using jacobian_t = typename T::Jacobian
-
template<typename T>
using path_accumulated_t = decltype(std::declval<T>().pathAccumulated)
-
template<typename T>
using state_t = typename T::State
-
template<typename T>
using step_size_t = decltype(std::declval<T>().stepSize)
Functions
-
METHOD_TRAIT(absolute_momentum_t, absoluteMomentum)
-
METHOD_TRAIT(bound_state_method_t, boundState)
-
METHOD_TRAIT(charge_t, charge)
-
METHOD_TRAIT(covariance_transport_bound_t, transportCovarianceToBound)
-
METHOD_TRAIT(covariance_transport_curvilinear_t, transportCovarianceToCurvilinear)
-
METHOD_TRAIT(curvilinear_state_method_t, curvilinearState)
-
METHOD_TRAIT(direction_t, direction)
-
METHOD_TRAIT(get_field_t, getField)
-
METHOD_TRAIT(get_step_size_t, getStepSize)
-
METHOD_TRAIT(momentum_t, momentum)
-
METHOD_TRAIT(output_step_size_t, outputStepSize)
-
METHOD_TRAIT(overstep_t, overstepLimit)
-
METHOD_TRAIT(position_t, position)
-
METHOD_TRAIT(qop_t, qOverP)
-
METHOD_TRAIT(release_step_size_t, releaseStepSize)
-
METHOD_TRAIT(reset_state_t, resetState)
-
METHOD_TRAIT(set_step_size_t, setStepSize)
-
METHOD_TRAIT(step_t, step)
-
METHOD_TRAIT(time_t, time)
-
METHOD_TRAIT(update_surface_status_t, updateSurfaceStatus)
-
METHOD_TRAIT(update_t, update)
Variables
-
template<typename S>
constexpr bool MultiStepperStateConcept = require<has_member<S, cov_transport_t, bool>, has_member<S, path_accumulated_t, double>>
-
template<typename S>
constexpr bool StepperStateConcept = require<has_member<S, cov_transport_t, bool>, has_member<S, cov_t, BoundSquareMatrix>, has_member<S, path_accumulated_t, double>>
-
template<typename S, typename state = typename S::State>
struct CommonStepperConcept - #include <Acts/Propagator/StepperConcept.hpp>
Public Static Attributes
-
static constexpr bool absolute_momentum_exists = has_method<const S, double, absolute_momentum_t, const state&>
-
static constexpr bool bound_state_exists = exists<bound_state_t, S>
-
static constexpr bool bound_state_method_exists = has_method<const S, Result<typename S::BoundState>, bound_state_method_t, state&, const Surface&, bool, const FreeToBoundCorrection&>
-
static constexpr bool charge_exists = has_method<const S, double, charge_t, const state&>
-
static constexpr bool covariance_exists = exists<covariance_t, S>
-
static constexpr bool covariance_transport_exists = require<has_method<const S, void, covariance_transport_curvilinear_t, state&>, has_method<const S, void, covariance_transport_bound_t, state&, const Surface&, const FreeToBoundCorrection&>>
-
static constexpr bool curvilinear_state_exists = exists<curvilinear_state_t, S>
-
static constexpr bool curvilinear_state_method_exists = has_method<const S, typename S::CurvilinearState, curvilinear_state_method_t, state&, bool>
-
static constexpr bool direction_exists = has_method<const S, Vector3, direction_t, const state&>
-
static constexpr bool get_step_size_exists = has_method<const S, double, get_step_size_t, const state&, ConstrainedStep::Type>
-
static constexpr bool jacobian_exists = exists<jacobian_t, S>
-
static constexpr bool momentum_exists = has_method<const S, Vector3, momentum_t, const state&>
-
static constexpr bool output_step_size_exists = has_method<const S, std::string, output_step_size_t, const state&>
-
static constexpr bool overstep_exists = has_method<const S, double, overstep_t, const state&>
-
static constexpr bool position_exists = has_method<const S, Vector3, position_t, const state&>
-
static constexpr bool qop_exists = has_method<const S, double, qop_t, const state&>
-
static constexpr bool release_step_size_exists = has_method<const S, void, release_step_size_t, state&>
-
static constexpr bool reset_state_exists = has_method<const S, void, reset_state_t, state&, const BoundVector&, const BoundSquareMatrix&, const Surface&, const double>
-
static constexpr bool set_step_size_exists = has_method<const S, void, set_step_size_t, state&, double, ConstrainedStep::Type, bool>
-
static constexpr bool time_exists = has_method<const S, double, time_t, const state&>
-
static constexpr bool update_surface_exists = has_method<const S, Intersection3D::Status, update_surface_status_t, state&, const Surface&, Direction, const BoundaryCheck&, ActsScalar, const Logger&>
-
static constexpr bool value = require<state_exists, jacobian_exists, covariance_exists, bound_state_exists, curvilinear_state_exists, position_exists, direction_exists, qop_exists, absolute_momentum_exists, momentum_exists, charge_exists, time_exists, bound_state_method_exists, curvilinear_state_method_exists, covariance_transport_exists, update_surface_exists, set_step_size_exists, release_step_size_exists, output_step_size_exists>
-
static constexpr bool absolute_momentum_exists = has_method<const S, double, absolute_momentum_t, const state&>
-
template<typename S, typename state = typename S::State>
struct MultiStepperConcept - #include <Acts/Propagator/StepperConcept.hpp>
Public Types
-
template<typename T>
using component_proxy_t = typename T::ComponentProxy
-
template<typename T>
using const_component_proxy_t = typename T::ConstComponentProxy
Public Functions
-
METHOD_TRAIT(clear_components_t, clearComponents)
-
METHOD_TRAIT(number_components_t, numberComponents)
-
METHOD_TRAIT(remove_missed_components_t, removeMissedComponents)
Public Static Attributes
-
static constexpr bool clear_components_exists = has_method<const S, void, clear_components_t, state&>
-
static constexpr bool common_stepper_concept_fullfilled = CommonStepperConcept<S, state>::value
-
static constexpr bool component_proxy_exists = exists<component_proxy_t, S>
-
static constexpr bool const_component_proxy_exists = exists<const_component_proxy_t, S>
-
static constexpr bool number_components_exists = has_method<const S, std::size_t, number_components_t, const state&>
-
static constexpr bool remove_missed_components_exists = has_method<const S, void, remove_missed_components_t, state&>
-
static constexpr bool value = require<common_stepper_concept_fullfilled, component_proxy_exists, const_component_proxy_exists, number_components_exists, clear_components_exists, remove_missed_components_exists>
-
template<typename T>
-
template<typename S, typename state = typename S::State>
struct SingleStepperConcept - #include <Acts/Propagator/StepperConcept.hpp>
Public Static Attributes
-
static constexpr bool common_stepper_concept_fullfilled = CommonStepperConcept<S, state>::value
-
static constexpr bool get_field_exists = has_method<const S, Result<Vector3>, get_field_t, state&, const Vector3&>
-
static constexpr bool update_method_exists = require<has_method<const S, void, update_t, state&, const FreeVector&, const BoundVector&, const BoundSquareMatrix&, const Surface&>, has_method<const S, void, update_t, state&, const Vector3&, const Vector3&, double, double>>
-
static constexpr bool value = require<common_stepper_concept_fullfilled, update_method_exists, get_field_exists>
-
static constexpr bool common_stepper_concept_fullfilled = CommonStepperConcept<S, state>::value
-
template<typename T>
-
namespace VertexFinder
Typedefs
-
template<typename T>
using state_t = typename T::State
Functions
-
METHOD_TRAIT(find_t, find)
-
template<typename S>
struct VertexFinderConcept - #include <Acts/Vertexing/VertexFinderConcept.hpp>
Public Static Attributes
-
static constexpr bool find_exists = has_method<const S, Result<std::vector<Vertex<typename S::InputTrack_t>>>, find_t, const std::vector<const typename S::InputTrack_t*>&, constVertexingOptions<typename S::InputTrack_t>&, typename S::State&>
-
static constexpr bool value = require<state_exists, find_exists>
-
static constexpr bool find_exists = has_method<const S, Result<std::vector<Vertex<typename S::InputTrack_t>>>, find_t, const std::vector<const typename S::InputTrack_t*>&, constVertexingOptions<typename S::InputTrack_t>&, typename S::State&>
-
template<typename T>
-
namespace VertexFitter
Typedefs
-
template<typename T>
using linearizer_t = typename T::Linearizer_t
-
template<typename T>
using propagator_t = typename T::Propagator_t
-
template<typename T>
using state_t = typename T::State
-
template<typename T>
using track_t = typename T::InputTrack_t
Functions
-
METHOD_TRAIT(fit_t, fit)
-
template<typename S>
struct VertexFitterConcept - #include <Acts/Vertexing/VertexFitterConcept.hpp>
Public Static Attributes
-
static constexpr bool fit_exists = has_method<const S, Result<Vertex<typename S::InputTrack_t>>, fit_t, const std::vector<const typename S::InputTrack_t*>&, const typename S::Linearizer_t&, constVertexingOptions<typename S::InputTrack_t>&, typename S::State&>
-
static constexpr bool linearizer_exists = exists<linearizer_t, S>
-
static constexpr bool propagator_exists = exists<propagator_t, S>
-
static constexpr bool value = require<fit_exists, track_exists, propagator_exists, linearizer_exists, state_exists>
-
static constexpr bool fit_exists = has_method<const S, Result<Vertex<typename S::InputTrack_t>>, fit_t, const std::vector<const typename S::InputTrack_t*>&, const typename S::Linearizer_t&, constVertexingOptions<typename S::InputTrack_t>&, typename S::State&>
-
template<typename T>
-
template<class Default, template<class...> class Op, class ...Args>
-
namespace DetectorJsonConverter
Functions
-
std::shared_ptr<Experimental::Detector> fromJson(const GeometryContext &gctx, const nlohmann::json &jDetector)
convert from json format
- Parameters
gctx – the geometry context
jDetector – the json object
- Returns
a newly created shared Detector object
-
nlohmann::json toJson(const GeometryContext &gctx, const Experimental::Detector &detector, const Options &options = Options{})
Convert to json format.
- Parameters
gctx – the geometry context
detector – the detector instance
options – the writing options that propagate to the downstream converters
- Returns
a json object
-
nlohmann::json toJsonDetray(const GeometryContext &gctx, const Experimental::Detector &detector, const Options &options = Options{})
Convert to detray json format.
- Parameters
gctx – the geometry context
detector – the detector instance
options – the writing options that propagate to the downstream converters
- Returns
a json object in detray format
-
struct Options
- #include <Acts/Plugins/Json/DetectorJsonConverter.hpp>
Public Members
-
DetectorVolumeJsonConverter::Options volumeOptions = DetectorVolumeJsonConverter::Options{}
-
DetectorVolumeJsonConverter::Options volumeOptions = DetectorVolumeJsonConverter::Options{}
-
std::shared_ptr<Experimental::Detector> fromJson(const GeometryContext &gctx, const nlohmann::json &jDetector)
-
namespace DetectorVolumeJsonConverter
Functions
-
std::shared_ptr<Experimental::DetectorVolume> fromJson(const GeometryContext &gctx, const nlohmann::json &jVolume)
convert from json format
Note
this only creates a volume in a stand-alone context, not in a detector context. For the latter, use the DetectorJsonConverter that will patch the portals accordingly
- Parameters
gctx – the geometry context
jVolume – the json object representing the detector volume
-
nlohmann::json toJson(const GeometryContext &gctx, const Experimental::DetectorVolume &volume, const std::vector<const Experimental::DetectorVolume*> &detectorVolumes, const std::vector<const Experimental::Portal*> &portals = {}, const Options &options = Options{})
Convert to json format.
- Parameters
gctx – the geometry context
volume – the detector volume instance
detectorVolumes – the list of other detector volumes
portals – the list of portals for saving the portal links
options – the options for the conversion
- Returns
a json object representing the detector volume
-
nlohmann::json toJsonDetray(const GeometryContext &gctx, const Experimental::DetectorVolume &volume, const std::vector<const Experimental::DetectorVolume*> &detectorVolumes, const Options &options = Options{})
Convert to json detray format.
- Parameters
gctx – the geometry context
volume – the detector volume instance
detectorVolumes – the list of other detector volumes
options – the options for the conversion
- Returns
a json object representing the detector volume
-
struct Options
- #include <Acts/Plugins/Json/DetectorVolumeJsonConverter.hpp>
Public Members
-
PortalJsonConverter::Options portalOptions
-
SurfaceJsonConverter::Options surfaceOptions
-
Transform3JsonConverter::Options transformOptions
-
PortalJsonConverter::Options portalOptions
-
std::shared_ptr<Experimental::DetectorVolume> fromJson(const GeometryContext &gctx, const nlohmann::json &jVolume)
-
namespace DetrayJsonHelper
Functions
-
static inline void addVolumeLink(nlohmann::json &jSurface, int vLink)
add volume link
- Parameters
jSurface – [in,out] is the json object to be patched
vLink – is the volume link to be added
-
static inline std::tuple<unsigned int, std::vector<ActsScalar>> maskFromBounds(const Acts::SurfaceBounds &sBounds, bool portal = false)
Helper function to switch keys from ACTS to detray.
DETRAY types
- Parameters
sBounds – is the surface bounds type
portal – is the flag for conversion into detray portal format
- Returns
type and value array in detray format
-
static inline void addVolumeLink(nlohmann::json &jSurface, int vLink)
-
namespace Experimental
Typedefs
-
using DetectorBlock = std::tuple<DetectorVolumes, ProtoContainer>
Current block (volumes and shell)
-
using DetectorBlockBuilder = std::function<void(DetectorBlock&, const GeometryContext&, Acts::Logging::Level)>
The detector builder function.
-
using DetectorVolumes = std::vector<std::shared_ptr<DetectorVolume>>
Current volumes (connected)
-
using DetectorVolumeUpdator = OwningDelegate<void(const GeometryContext &gctx, NavigationState &nState), INavigationDelegate>
Declare a Detctor Volume finding or switching delegate.
- Param gctx
is the current geometry context
- Param nState
[in, out] is the navigation state to be updated
- Return
the new DetectorVolume into which one changes at this switch
-
template<typename grid_type>
using IndexedDetectorVolumeImpl = IndexedUpdatorImpl<grid_type, IndexedDetectorVolumeExtractor, DetectorVolumeFiller> An indexed volume implementation access.
- Template Parameters
grid_type – is the grid type used for this
-
template<typename grid_type, template<typename> class indexed_updator>
using IndexedSurfacesAllPortalsImpl = ChainedUpdatorImpl<AllPortalsImpl, indexed_updator<grid_type>> An indexed surface implementation with portal access.
- Template Parameters
inexed_updator – is the updator for the indexed surfaces
-
template<typename grid_type>
using IndexedSurfacesImpl = IndexedUpdatorImpl<grid_type, IndexedSurfacesExtractor, SurfacesFiller> An indexed surface implementation access.
- Template Parameters
grid_type – is the grid type used for this indexed lookup
-
using PortalGenerator = Delegate<std::vector<std::shared_ptr<Portal>>(const Transform3&, const VolumeBounds&, const std::shared_ptr<DetectorVolume>&)>
The Portal generator definition.
-
using ProtoContainer = std::map<unsigned int, std::shared_ptr<Portal>>
Current shell (i.e. outside portals)
-
using SingleIndex = std::size_t
-
using SurfaceCandidatesUpdator = OwningDelegate<void(const GeometryContext &gctx, NavigationState &nState), INavigationDelegate>
Declare an updator for the local navigation, i.e.
the navigation inside a detector volume. This can be called either directly after a volume switch or in order to update within a volume after some progression
This delegate dispatches the local navigation action to a dedicated struct or function that is optimised for the given environment.
Note
it relies on the detector volume to be set to the state Memory managed navigation state updator
- Param gctx
is the current geometry context
- Param nState
[in,out] is the navigation state to be updated
-
using VariableBoundAxis = Acts::detail::Axis<Acts::detail::AxisType::Variable, Acts::detail::AxisBoundaryType::Bound>
-
using VariableBoundIndexGrid1 = Acts::detail::Grid<SingleIndex, VariableBoundAxis>
Enums
-
enum class GsfError
Values:
-
enumerator StartParametersNotOnStartSurface
-
enumerator StartParametersHaveNoCovariance
-
enumerator NoMeasurementStatesCreatedForward
-
enumerator NoMeasurementStatesCreatedBackward
-
enumerator NoMeasurementStatesCreatedFinal
-
enumerator StartParametersNotOnStartSurface
Functions
-
PortalGenerator defaultPortalAndSubPortalGenerator()
Create a default portal generator that connects to the static method.
Note
parameters are ignored in this case
-
PortalGenerator defaultPortalGenerator()
Create a default portal generator that connects to the static method.
Generator function for creation of portal surfaces.
- Parameters
dTransform – a contextually resolved transform
dBounds – the detecor volume bounds
dVolume – the reference to the detector volume which generates this volume
- Returns
a vector of newly created portals with registered inside volume
Calls the portal generation and adds registration to sub portals.
This code is split off the PortalGenerator code in order to allow unit testing of the portal generation without detector volume construction
- Parameters
dTransform – a contextually resolved transform
dBounds – the detecor volume bounds
dVolume – the reference to the detector volume which generates this volume
- Returns
a vector of newly created portals with registered inside volume
-
std::error_code make_error_code(GsfError e)
-
AtlasBetheHeitlerApprox<6, 5> makeDefaultBetheHeitlerApprox()
Creates a AtlasBetheHeitlerApprox object based on an ATLAS configuration, that are stored as static data in the source code.
This may not be an optimal configuration, but should allow to run the GSF without the need to load files
-
static inline SurfaceCandidatesUpdator tryAllPortals()
Generate a provider for all portals.
- Returns
a connected navigationstate updator
-
static inline SurfaceCandidatesUpdator tryAllPortalsAndSurfaces()
Generate a provider for all portals and Surfacess.
Note
this is a try-and error navigation, not recommended for production setup with many surfaces
- Returns
a connected navigationstate updator
-
static inline DetectorVolumeUpdator tryAllSubVolumes()
Generate a delegate to try all sub volumes.
-
static inline DetectorVolumeUpdator tryNoVolumes()
Generate a delegate to try no volume.
-
static inline DetectorVolumeUpdator tryRootVolumes()
Generate a delegate to try the root volumes.
-
static inline DetectorVolumeUpdator unconnectedUpdator()
A dummy constructed updator.
Helper method to update the candidates (portals/surfaces), this can be called for initial surface/portal estimation, but also during the navigation to update the current list of candidates.
- Parameters
gctx – is the Geometry context of this call
nState – [in,out] is the navigation state to be updated
-
struct AdditionalSurfacesImpl : public Acts::Experimental::INavigationDelegate
- #include <Acts/Navigation/SurfaceCandidatesUpdators.hpp>
This holds and extracts a collection of surfaces without much checking, this could be e.g.
support surfaces for layer structures, e.g.
Public Functions
Extract the sub volumes from the volume.
- Parameters
gctx – the geometry contextfor this extraction call (ignored)
nState – is the navigation state
Public Members
-
std::vector<const Surface*> surfaces = {}
The volumes held by this collection.
-
struct AllPortalsAndSurfacesImpl : public Acts::Experimental::INavigationDelegate
- #include <Acts/Navigation/SurfaceCandidatesUpdators.hpp>
Public Functions
An ordered list of portals and surfaces provider.
Note
that the intersections are ordered, such that the smallest intersection pathlength >= overstep tolerance is the lowest
- Parameters
gctx – is the Geometry context of this call
nState – is the navigation state to be updated
- Returns
an ordered list of portal and surface candidates
-
struct AllPortalsExtractor
- #include <Acts/Detector/DetectorVolume.hpp>
Helper extractors: all portals.
Public Static Functions
Extract the portals from the volume.
- Parameters
gctx – the geometry contextfor this extraction call
nState – is the current navigation state
- Returns
a vector of raw Portal pointers
-
struct AllPortalsImpl : public Acts::Experimental::INavigationDelegate
- #include <Acts/Navigation/SurfaceCandidatesUpdators.hpp>
Public Functions
A ordered portal provider.
Note
that the intersections are ordered, such that the smallest intersection pathlength >= overstep tolerance is the lowest
- Parameters
gctx – is the Geometry context of this call
nState – is the navigation state to be updated
- Returns
an ordered list of portal candidates
-
struct AllSubVolumesExtractor
- #include <Acts/Detector/DetectorVolume.hpp>
Helper extractors: all sub volumes of a volume.
Public Static Functions
Extract the sub volumes from the volume.
- Parameters
gctx – the geometry contextfor this extraction call
nState – is the current navigation state
indices – are access indices into the volume store (ignored)
- Returns
a vector of raw DetectorVolume pointers
-
struct AllSurfacesExtractor
- #include <Acts/Detector/DetectorVolume.hpp>
Helper extractors: all surfaces.
Public Static Functions
Extract the surfaces from the volume.
- Parameters
gctx – the geometry contextfor this extraction call
nState – is the current navigation state
indices – is an ignored index vector
- Returns
a vector of raw Surface pointers
-
template<int NComponents, int PolyDegree>
class AtlasBetheHeitlerApprox - #include <Acts/TrackFitting/BetheHeitlerApprox.hpp>
This class approximates the Bethe-Heitler distribution as a gaussian mixture.
To enable an approximation for continuous input variables, the weights, means and variances are internally parametrized as a Nth order polynomial.
Public Types
-
using Data = std::array<PolyData, NComponents>
Public Functions
-
inline constexpr AtlasBetheHeitlerApprox(const Data &low_data, const Data &high_data, bool low_transform, bool high_transform)
Construct the Bethe-Heitler approximation description.
Additional to the coefficients of the polynomials, the information whether these values need to be transformed beforehand must be given (see ATLAS code).
- Parameters
low_data – data for the lower x/x0 range
high_data – data for the higher x/x0 range
low_transform – whether the low data need to be transformed
high_transform – whether the high data need to be transformed
-
inline auto mixture(ActsScalar x) const
Generates the mixture from the polynomials and reweights them, so that the sum of all weights is 1.
- Parameters
x – pathlength in terms of the radiation length
-
inline constexpr auto numComponents() const
Returns the number of components the returned mixture will have.
-
inline constexpr bool validXOverX0(ActsScalar x) const
Checks if an input is valid for the parameterization.
- Parameters
x – pathlength in terms of the radiation length
Public Static Functions
-
static inline auto loadFromFiles(const std::string &low_parameters_path, const std::string &high_parameters_path)
Loads a parameterization from a file according to the Atlas file description.
- Parameters
low_parameters_path – Path to the foo.par file that stores the parameterization for low x/x0
high_parameters_path – Path to the foo.par file that stores the parameterization for high x/x0
Public Static Attributes
-
static constexpr double higherLimit = 0.20
-
static constexpr double lowerLimit = 0.10
-
static constexpr double noChangeLimit = 0.0001
-
static constexpr double singleGaussianLimit = 0.002
-
struct PolyData
- #include <Acts/TrackFitting/BetheHeitlerApprox.hpp>
Public Members
-
std::array<ActsScalar, PolyDegree + 1> meanCoeffs
-
std::array<ActsScalar, PolyDegree + 1> varCoeffs
-
std::array<ActsScalar, PolyDegree + 1> weightCoeffs
-
std::array<ActsScalar, PolyDegree + 1> meanCoeffs
-
using Data = std::array<PolyData, NComponents>
-
struct BetheHeitlerApproxSingleCmp
- #include <Acts/TrackFitting/BetheHeitlerApprox.hpp>
This class approximates the Bethe-Heitler with only one component.
This is mainly inside AtlasBetheHeitlerApprox, but can also be used as the only component approximation (then probably for debugging)
Public Functions
-
inline constexpr auto numComponents() const
Returns the number of components the returned mixture will have.
-
inline constexpr bool validXOverX0(ActsScalar x) const
Checks if an input is valid for the parameterization.
The threshold for x/x0 is 0.002 and orientates on the values used in ATLAS
Public Static Functions
-
static inline auto mixture(const ActsScalar x)
Returns array with length 1 containing a 1-component-representation of the Bethe-Heitler-Distribution.
- Parameters
x – pathlength in terms of the radiation length
-
inline constexpr auto numComponents() const
-
struct BoundVolumesGrid1Impl : public Acts::Experimental::INavigationDelegate
- #include <Acts/Navigation/DetectorVolumeUpdators.hpp>
This is used for volumes that are indexed in a bound 1-dimensional grid, e.g.
a z-spaced array, or an r-spaced array of volumes.
Public Types
-
using IndexedUpdator = IndexedUpdatorImpl<VariableBoundIndexGrid1, DetectorVolumesCollection, DetectorVolumeFiller>
Public Functions
-
BoundVolumesGrid1Impl() = delete
-
inline BoundVolumesGrid1Impl(const std::vector<ActsScalar> &gBoundaries, BinningValue bValue, const std::vector<const DetectorVolume*> &cVolumes, const Transform3 &bTransform = Transform3::Identity()) noexcept(false)
Allowed constructor with explicit arguments.
- Parameters
gBoundaries – the grid boundaries
bValue – the binning value
cVolumes – the contained volumes
bTransform – is the optional transform
This updator relies on an 1D single index grid.
- Parameters
gctx – the geometry context
nState – [in,out] the navigation state to be updated
Public Members
-
IndexedUpdator indexedUpdator
-
using IndexedUpdator = IndexedUpdatorImpl<VariableBoundIndexGrid1, DetectorVolumesCollection, DetectorVolumeFiller>
-
template<typename ...updators_t>
class ChainedUpdatorImpl : public Acts::Experimental::INavigationDelegate - #include <Acts/Navigation/NavigationStateUpdators.hpp>
This is a chained extractor/filler implementation Since there is no control whether it is a static or payload extractor, these have to be provided by a tuple.
- Template Parameters
updators_t – the updators that will be called in sequence
Public Functions
-
inline ChainedUpdatorImpl(const std::tuple<updators_t...> &&upts)
Constructor for chained updators in a tuple, this will unroll the tuple and call them in sequence.
- Parameters
upts – the updators to be called in chain
A combined navigation state updator w/o intersection specifics.
- Parameters
gctx – is the Geometry context of this call
nState – the navigation state to which the objects are attached
Public Members
-
std::tuple<updators_t...> updators
The stored updators.
-
class CylindricalContainerBuilder : public Acts::Experimental::IDetectorComponentBuilder
- #include <Acts/Detector/CylindricalContainerBuilder.hpp>
A dedicated container builder for cylindrical detector containers.
It relies on the detailed implementation of the CylindricalDetectorHelper and allows for DetectorVolume attachment in z/r/phi, such as wrapping of bevelled cylinder objects in z/r
Note
the builder expects a fully consistent set of sub volume builders that will be executed in a chain
Note
allowed BinningValue(s) for the cylindrical container builder are {binZ}, {binR}, {binPhi}, {binZ, binR}, whereas the last option indicates a wrapping setup.
Public Functions
-
CylindricalContainerBuilder(const Config &cfg, std::unique_ptr<const Logger> logger = getDefaultLogger("CylindricalContainerBuilder", Logging::INFO))
Constructor with configuration arguments.
- Parameters
cfg – is the configuration struct
logger – logging instance for screen output
-
virtual DetectorComponent construct(const GeometryContext &gctx) const final
The final implementation of the cylindrical container builder.
- Parameters
gctx – The geometry context for this call
- Returns
an outgoing detector component
-
struct Config
- #include <Acts/Detector/CylindricalContainerBuilder.hpp>
Nested configuration object.
Public Members
-
std::string auxiliary = ""
Auxiliary information, mainly for screen output.
-
std::vector<BinningValue> binning = {}
Binning prescription of attachment.
-
std::vector<std::shared_ptr<const IDetectorComponentBuilder>> builders = {}
The configured volume builders.
-
std::string auxiliary = ""
-
CylindricalContainerBuilder(const Config &cfg, std::unique_ptr<const Logger> logger = getDefaultLogger("CylindricalContainerBuilder", Logging::INFO))
-
class Detector : public std::enable_shared_from_this<Detector>
- #include <Acts/Detector/Detector.hpp>
Public Functions
-
const DetectorVolumeUpdator &detectorVolumeFinder() const
Const access to the volume finder.
-
const DetectorVolume *findDetectorVolume(const GeometryContext &gctx, const Vector3 &position) const
Find a volume from a position.
Note
this creates internally a NavigationState object
- Parameters
gctx – is the Geometry context of the call
position – is the position of the call
- Returns
the volume pointer or nullptr (if outside)
-
const DetectorVolume *findDetectorVolume(const std::string &name) const
Find a volume by name.
- Parameters
name – with which the volume is searched for
- Returns
the volume pointer or nullptr (if not found)
Retrieve a
std::shared_ptrfor this surface (non-const version)Note
Will error if this was not created through the
makeSharedfactory since it needs access to the original reference. In C++14 this is undefined behavior (but most likely implemented as abad_weak_ptrexception), in C++17 it is defined as that exception.Note
Only call this if you need shared ownership of this object.
- Returns
The shared pointer
Retrieve a
std::shared_ptrfor this surface (const version)Note
Will error if this was not created through the
makeSharedfactory since it needs access to the original reference. In C++14 this is undefined behavior, but most likely implemented as abad_weak_ptrexception, in C++17 it is defined as that exception.Note
Only call this if you need shared ownership of this object.
- Returns
The shared pointer
-
const std::string &name() const
Return the name of the detector.
-
std::vector<std::shared_ptr<DetectorVolume>> &rootVolumePtrs()
Non-const access to the root volumes.
- Returns
the root volume shared pointer
-
const std::vector<const DetectorVolume*> &rootVolumes() const
Const access to the root volumes.
- Returns
a vector to const DetectorVolume raw pointers
Update the current volume of a given navigation state.
- Parameters
gctx – is the Geometry context of the call
nState – [in, out] is the navigation state
-
void updateDetectorVolumeFinder(DetectorVolumeUpdator detectorVolumeUpdator)
Update the volume finder.
- Parameters
detectorVolumeUpdator – the new volume finder
-
std::vector<std::shared_ptr<DetectorVolume>> &volumePtrs()
Non-const access to the root volume.
- Returns
the volumes shared pointer store
-
const std::vector<const DetectorVolume*> &volumes() const
Const access to sub volumes.
- Returns
a vector to const DetectorVolume raw pointers
Public Static Functions
Factory for producing memory managed instances of Detector.
-
const DetectorVolumeUpdator &detectorVolumeFinder() const
-
class DetectorBuilder : public Acts::Experimental::IDetectorBuilder
- #include <Acts/Detector/DetectorBuilder.hpp>
Standard generic Detector builder that calls the top level component builder and transfers the result into a detector object.
Note
This is the last builder in the chain and the the returned detector object is const and cannot be modified anymore.
Public Functions
-
DetectorBuilder(const Config &cfg, std::unique_ptr<const Logger> mlogger = getDefaultLogger("DetectorBuilder", Logging::INFO))
Constructor with configuration arguments.
- Parameters
cfg – is the configuration struct
mlogger – logging instance for screen output
-
virtual std::shared_ptr<const Detector> construct(const GeometryContext &gctx) const final
Final implementation of a volume builder that is purely defined by an internal and external structure builder.
- Parameters
gctx – The geometry context for this call
- Returns
an outgoing detector component
-
struct Config
- #include <Acts/Detector/DetectorBuilder.hpp>
Nested configuration object.
Public Members
-
std::string auxiliary = ""
Auxiliary information.
-
std::shared_ptr<const IDetectorComponentBuilder> builder = nullptr
An external builder.
-
std::string name = "unnamed"
The name of the volume to be built.
-
std::string auxiliary = ""
-
DetectorBuilder(const Config &cfg, std::unique_ptr<const Logger> mlogger = getDefaultLogger("DetectorBuilder", Logging::INFO))
-
struct DetectorComponent
- #include <Acts/Detector/DetectorComponents.hpp>
The currently built detector components including the constructed volumes and the current shell/coating, i.e.
portals ordered in a map
Note
the map indices of the shell coating represent their respective index in the portal vector of the VolumeBounds derivative that is described by the given component.
Public Types
-
using PortalContainer = std::map<unsigned int, std::shared_ptr<Portal>>
Define a portal container.
Public Members
-
PortalContainer portals = {}
The current map of outside portals.
-
RootDetectorVolumes rootVolumes = {}
The root volumes finder.
-
std::vector<std::shared_ptr<DetectorVolume>> volumes = {}
The vector of constructed volume(s)
-
using PortalContainer = std::map<unsigned int, std::shared_ptr<Portal>>
- #include <Acts/Navigation/DetectorNavigator.hpp>
Public Functions
Constructor with configuration object.
- Parameters
cfg – The navigator configuration
_logger – a logger instance
Initialize call - start of propagation.
- Template Parameters
propagator_state_t – The state type of the propagagor
stepper_t – The type of stepper used for the propagation
- Parameters
state – [inout] is the propagation state object
stepper – [in] Stepper in use
- Returns
boolean return triggers exit to stepper
Navigator post step call.
- Template Parameters
propagator_state_t – is the type of Propagatgor state
stepper_t – is the used type of the Stepper by the Propagator
- Parameters
state – [inout] is the mutable propagator state object
stepper – [in] Stepper in use
Navigator pre step call.
This will invalid the current surface and current portal in order to navigate to the next ones.
- Template Parameters
propagator_state_t – is the type of Propagatgor state
stepper_t – is the used type of the Stepper by the Propagator
- Parameters
state – [inout] is the mutable propagator state object
stepper – [in] Stepper in use
- #include <Acts/Navigation/DetectorNavigator.hpp>
Public Members
Detector for this Navigation.
stop at every material surface (whether it is passive or not)
stop at every surface regardless what it is
Configuration for this Navigator stop at every sensitive surface (whether it has material or not)
- #include <Acts/Navigation/DetectorNavigator.hpp>
Nested State struct.
It acts as an internal state which is created for every propagation/extrapolation step and keep thread-local navigation information
Public Members
Navigation state - external state: the current surface.
Navigation state : a break has been detected.
Navigation state - external state: the start surface.
Indicator if the target is reached.
Navigation state - external state: the target surface.
-
class DetectorVolume : public std::enable_shared_from_this<DetectorVolume>
- #include <Acts/Detector/DetectorVolume.hpp>
A detector volume description which can be:
Note
A detector volume holds non-const objects internally that are allowed to be modified as long as the geometry is not yet closed. Using this, material can be attached, and GeometryIdentifier can be set at construction time.
Note
The construction of DetectorVolumes is done via a dedicated factory, this is necessary as then the shared_ptr is non-weak and it can be registered in the portal generator for further geometry processing.
Note
Navigation is always done by plain pointers, while object ownership is done by shared/unique pointers.
Public Types
-
using BoundingBox = Acts::AxisAlignedBoundingBox<Acts::Experimental::DetectorVolume, Acts::ActsScalar, 3>
Public Functions
-
void assignDetector(const Detector &detector)
Assign Detector to this volume (for back navigation issues)
- Parameters
detector – the parenting detector class
This method allows to udate the navigation state updator module.
- Parameters
surfaceCandidateUpdator – the new navigation state updator for surfaces
surfaces – the surfaces the new navigation state updator points to
volumes – the volumes the new navigation state updator points to
Assign the volume material description.
This method allows to load a material description during the detector geometry building, and assigning it (potentially multiple) times to detector volumes.
- Parameters
material – Material description associated to this volumw
-
Vector3 center(const GeometryContext &gctx = GeometryContext()) const
Const access to the center.
Note
the geometry context is currently ignored, but is a placeholder for eventually misaligned volumes
- Parameters
gctx – the geometry context
- Returns
a contextually created center
-
void closePortals()
Final closing of portal, i.e. this sets the end of world.
-
const Detector *detector() const
Const access to the detector.
-
const DetectorVolumeUpdator &detectorVolumeUpdator() const
Const access to the detector volume updator.
-
bool exclusivelyInside(const GeometryContext &gctx, const Vector3 &position) const
Check if a point is exclusively inside this volume i.e.
this point is not inside a subvolume.
- Parameters
gctx – the geometry context
position – the position for the inside check
- Returns
a bool to indicate inside/outside
-
Extent extent(const GeometryContext &gctx, size_t nseg = 1) const
The Extent for this volume.
- Parameters
gctx – is the geometry context
nseg – is the number of segments to approximate
- Returns
an Extent object
-
const GeometryIdentifier &geometryId() const
- Returns
the geometry identifier
-
const BoundingBox &getBoundingBox() const
Retrieve a
std::shared_ptrfor this surface (non-const version)Note
Will error if this was not created through the
makeSharedfactory since it needs access to the original reference. In C++14 this is undefined behavior (but most likely implemented as abad_weak_ptrexception), in C++17 it is defined as that exception.Note
Only call this if you need shared ownership of this object.
- Returns
The shared pointer
Retrieve a
std::shared_ptrfor this surface (const version)Note
Will error if this was not created through the
makeSharedfactory since it needs access to the original reference. In C++14 this is undefined behavior, but most likely implemented as abad_weak_ptrexception, in C++17 it is defined as that exception.Note
Only call this if you need shared ownership of this object.
- Returns
The shared pointer
-
bool inside(const GeometryContext &gctx, const Vector3 &position) const
Check if a point is inside this volume.
Subvolumes will not be checked.
- Parameters
gctx – the geometry context
position – the position for the inside check
- Returns
a bool to indicate inside/outside
-
const std::string &name() const
- Returns
the name of the volume
-
std::vector<std::shared_ptr<Portal>> &portalPtrs()
Non-const access to the portals.
- Returns
the portal shared pointer store
-
const std::vector<const Portal*> &portals() const
Const access to the detector portals.
Note
an empty vector indicates a container volume that has not been properly connected
- Returns
a vector to const Portal raw pointers
-
const SurfaceCandidatesUpdator &surfaceCandidatesUpdator() const
Const access to the navigation state updator.
-
std::vector<std::shared_ptr<Surface>> &surfacePtrs()
Non-const access to the surfaces.
- Returns
the surfaces shared pointer store
-
const std::vector<const Surface*> &surfaces() const
Const access to the surfaces.
Note
an empty vector indicates either gap volume or container volume, a non-empty vector indicates a layer volume.
- Returns
a vector to const Surface raw pointers
-
const Transform3 &transform(const GeometryContext &gctx = GeometryContext()) const
Const access to the transform.
Note
the geometry context is currently ignored, but is a placeholder for eventually misaligned volumes
- Parameters
gctx – the geometry context
- Returns
const reference to the contextual transform
Initialize/update the navigation status in this environment.
This method calls:
the local navigation delegate for candidate surfaces
the portal navigation delegate for candidate exit portals
set the current detector volume
- Parameters
gctx – is the current geometry context
nState – [in,out] is the detector navigation state to be updated
Update a portal given a portal index.
Note
throws exception if portal index out of bounds
- Parameters
portal – the portal to be updated
pIndex – the portal index
-
const VolumeBounds &volumeBounds() const
Const access to the volume bounds.
- Returns
const reference to the volume bounds object
-
const IVolumeMaterial *volumeMaterial() const
Const access to the volume amterial.
-
std::shared_ptr<IVolumeMaterial> volumeMaterialPtr()
Non-const access to the voume material (for scaling, e.g.)
-
std::vector<std::shared_ptr<DetectorVolume>> &volumePtrs()
Non-const access to the volumes.
- Returns
the volumes shared pointer store
-
const std::vector<const DetectorVolume*> &volumes() const
Const access to sub volumes.
Note
and empty vector indicates this is either a gap volume or a layer volume, in any case it means the volume is on navigation level and the portals need to be connected
- Returns
a vector to const DetectorVolume raw pointers
Friends
- friend class DetectorVolumeFactory
-
template<typename internal_type>
struct ObjectStore - #include <Acts/Detector/DetectorVolume.hpp>
Nested object store that holds the internal (non-const), reference counted objects and provides an external (const raw pointer) access.
- Template Parameters
internal_type – is the internal storage representation, has to comply with std::shared_ptr semantics
Public Functions
-
ObjectStore() = default
-
inline ObjectStore(std::vector<internal_type> objects)
Store constructor.
- Parameters
objects – are the ones copied into the internal store
Public Members
-
std::vector<const typename internal_type::element_type*> external = {}
The external storage vector, const raw pointer.
-
std::vector<internal_type> internal = {}
The internal storage vector.
-
using BoundingBox = Acts::AxisAlignedBoundingBox<Acts::Experimental::DetectorVolume, Acts::ActsScalar, 3>
-
class DetectorVolumeBuilder : public Acts::Experimental::IDetectorComponentBuilder
- #include <Acts/Detector/DetectorVolumeBuilder.hpp>
A generic detector volume builder that uses an external builder for shape and portals and an internal structure builder for volume internals.
Note
Although this helper builds only a single volume, it is to the outside presented as a DetectorComponent with shell; like this it can be transparently be used for the downstream detector construction process.
Public Functions
-
DetectorVolumeBuilder(const Config &cfg, std::unique_ptr<const Logger> mlogger = getDefaultLogger("DetectorVolumeBuilder", Logging::INFO))
Constructor with configuration arguments.
- Parameters
cfg – is the configuration struct
mlogger – logging instance for screen output
-
virtual DetectorComponent construct(const GeometryContext &gctx) const final
Final implementation of a volume builder that is purely defined by an internal and external structure builder.
- Parameters
gctx – The geometry context for this call
- Returns
an outgoing detector component
-
struct Config
- #include <Acts/Detector/DetectorVolumeBuilder.hpp>
Nested configuration object.
Public Members
-
bool addInternalsToRoot = false
Add eventual internal volume to root.
-
std::string auxiliary = ""
Auxiliary information.
-
std::shared_ptr<const IExternalStructureBuilder> externalsBuilder = nullptr
An external builder.
-
std::shared_ptr<const IInternalStructureBuilder> internalsBuilder = nullptr
An internal builder.
-
std::string name = "unnamed"
The name of the volume to be built.
-
bool addInternalsToRoot = false
-
DetectorVolumeBuilder(const Config &cfg, std::unique_ptr<const Logger> mlogger = getDefaultLogger("DetectorVolumeBuilder", Logging::INFO))
-
class DetectorVolumeFactory
- #include <Acts/Detector/DetectorVolume.hpp>
A detector volume factory which first constructs the detector volume and then constructs the portals.
This ensures that the std::shared_ptr holding the detector volume is not weak when assigning to the portals.
Public Static Functions
Create a detector volume - from factory.
Create a detector volume - from factory.
-
struct DetectorVolumeFiller
- #include <Acts/Navigation/NavigationStateFillers.hpp>
Filler of the current volume.
Public Static Functions
Helper struct that allows to fill a volume into the navigation state, it allows to use common navigation structs for volume, portal, surfaces.
- Parameters
nState – the navigation state
volume – the volume that is filled
-
struct DetectorVolumesCollection
- #include <Acts/Navigation/DetectorVolumeUpdators.hpp>
This holds and extracts a collection of detector volumes.
Alternatively an extractor could also use the detector and its associated detector volume container for volume extraction.
Public Functions
Extract a voume from a collection.
Note
that geometry context and navigation state are ignored here
- Parameters
index – are access indices into the surfaces store
- Returns
the extracted volume
Public Members
-
std::vector<const DetectorVolume*> dVolumes = {}
The volumes held by this collection.
-
struct EndOfWorldImpl : public Acts::Experimental::INavigationDelegate
- #include <Acts/Navigation/DetectorVolumeUpdators.hpp>
The end of world sets the volume pointer of the navigation state to nullptr, usually indicates the end of the known world, hence the name.
Public Functions
a null volume link - explicitly
Note
the method parameters are ignored
-
struct ExternalStructure
- #include <Acts/Detector/DetectorComponents.hpp>
Holder struct for the external structure components required to construct a detectorVolume.
Public Members
-
std::unique_ptr<VolumeBounds> bounds = nullptr
A shape definition.
-
PortalGenerator portalGenerator
And a portal generator.
-
Transform3 transform = Transform3::Identity()
A 3D transform where the volume should be positioned.
-
std::unique_ptr<VolumeBounds> bounds = nullptr
-
template<typename propagator_t, typename bethe_heitler_approx_t, typename traj_t>
struct GaussianSumFitter - #include <Acts/TrackFitting/GaussianSumFitter.hpp>
Gaussian Sum Fitter implementation.
Note
This GSF implementation tries to be as compatible to the KalmanFitter as possible. However, strict compatibility is not garantueed.
Note
Currently there is no possibility to export the states of the individual components from the GSF, the only information returned in the MultiTrajectory are the means of the states. Therefore, also NO dedicated component smoothing is performed as described e.g. by R. Fruewirth.
- Template Parameters
propagator_t – The propagator type on which the algorithm is built on
bethe_heitler_approx_t – The type of the Bethe-Heitler-Approximation
traj_t – The MultiTrajectory type (backend)
Public Types
-
using GsfActor = detail::GsfActor<bethe_heitler_approx_t, traj_t>
The actor type.
The navigator type.
Public Functions
-
inline GaussianSumFitter(propagator_t &&propagator, bethe_heitler_approx_t &&bha, std::unique_ptr<const Logger> _logger = getDefaultLogger("GSF", Logging::INFO))
-
template<typename source_link_it_t, typename start_parameters_t, typename track_container_t, template<typename> class holder_t>
inline auto fit(source_link_it_t begin, source_link_it_t end, const start_parameters_t &sParameters, const GsfOptions<traj_t> &options, const std::vector<const Surface*> &sSequence, TrackContainer<track_container_t, traj_t, holder_t> &trackContainer) const The fit function for the Direct navigator.
-
template<typename source_link_it_t, typename start_parameters_t, typename track_container_t, template<typename> class holder_t>
inline auto fit(source_link_it_t begin, source_link_it_t end, const start_parameters_t &sParameters, const GsfOptions<traj_t> &options, TrackContainer<track_container_t, traj_t, holder_t> &trackContainer) const The fit function for the standard navigator.
-
template<typename source_link_it_t, typename start_parameters_t, typename fwd_prop_initializer_t, typename bwd_prop_initializer_t, typename track_container_t, template<typename> class holder_t>
inline Acts::Result<typename TrackContainer<track_container_t, traj_t, holder_t>::TrackProxy> fit_impl(source_link_it_t begin, source_link_it_t end, const start_parameters_t &sParameters, const GsfOptions<traj_t> &options, const fwd_prop_initializer_t &fwdPropInitializer, const bwd_prop_initializer_t &bwdPropInitializer, TrackContainer<track_container_t, traj_t, holder_t> &trackContainer) const The generic implementation of the fit function.
TODO check what this function does with the referenceSurface is e.g. the first measuerementSurface
-
inline const Logger &logger() const
Public Members
-
std::unique_ptr<const Logger> m_actorLogger
-
bethe_heitler_approx_t m_betheHeitlerApproximation
The fitter holds the instance of the bethe heitler approx.
-
std::unique_ptr<const Logger> m_logger
The logger.
-
propagator_t m_propagator
The propagator instance used by the fit function.
-
template<typename traj_t>
struct GsfExtensions - #include <Acts/TrackFitting/GsfOptions.hpp>
The extensions needed for the GSF.
Public Types
-
using Calibrator = Delegate<void(const GeometryContext&, const CalibrationContext&, const SourceLink&, TrackStateProxy)>
-
using ConstTrackStateProxy = typename traj_t::ConstTrackStateProxy
-
using OutlierFinder = Delegate<bool(ConstTrackStateProxy)>
-
using TrackStateProxy = typename traj_t::TrackStateProxy
-
using Updater = Delegate<Result<void>(const GeometryContext&, TrackStateProxy, Direction, const Logger&)>
Public Functions
-
inline GsfExtensions()
Default constructor which connects the default void components.
Public Members
-
Calibrator calibrator
The Calibrator is a dedicated calibration algorithm that allows to calibrate measurements using track information, this could be e.g.
sagging for wires, module deformations, etc.
-
OutlierFinder outlierFinder
Determines whether a measurement is supposed to be considered as an outlier.
-
SourceLinkSurfaceAccessor surfaceAccessor
Retrieves the associated surface from a source link.
-
Updater updater
The updater incorporates measurement information into the track parameters.
-
using Calibrator = Delegate<void(const GeometryContext&, const CalibrationContext&, const SourceLink&, TrackStateProxy)>
-
template<typename traj_t>
struct GsfOptions - #include <Acts/TrackFitting/GsfOptions.hpp>
Public Functions
-
GsfOptions() = delete
Public Members
-
bool abortOnError = false
-
std::reference_wrapper<const CalibrationContext> calibrationContext
-
bool disableAllMaterialHandling = false
-
GsfExtensions<traj_t> extensions
-
std::string_view finalMultiComponentStateColumn = ""
-
std::reference_wrapper<const GeometryContext> geoContext
-
std::reference_wrapper<const MagneticFieldContext> magFieldContext
-
std::size_t maxComponents = 4
-
PropagatorPlainOptions propagatorPlainOptions
-
const Surface *referenceSurface = nullptr
-
MixtureReductionMethod stateReductionMethod = MixtureReductionMethod::eMaxWeight
-
double weightCutoff = 1.e-4
-
GsfOptions() = delete
-
template<typename propagator_t, typename traj_t>
class Gx2Fitter - #include <Acts/TrackFitting/GlobalChiSquareFitter.hpp>
Global Chi Square fitter (GX2F) implementation.
TODO Write description
- Template Parameters
propagator_t – Type of the propagation class
Public Functions
-
inline Gx2Fitter(propagator_t pPropagator, std::unique_ptr<const Logger> _logger = getDefaultLogger("Gx2Fitter", Logging::INFO))
-
template<typename source_link_iterator_t, typename start_parameters_t, typename parameters_t = BoundTrackParameters, typename track_container_t, template<typename> class holder_t, bool _isdn = isDirectNavigator>
inline auto fit(source_link_iterator_t it, source_link_iterator_t end, const start_parameters_t &sParameters, const Gx2FitterOptions<traj_t> &gx2fOptions, TrackContainer<track_container_t, traj_t, holder_t> &trackContainer) const -> std::enable_if_t<!_isdn, Result<typename TrackContainer<track_container_t, traj_t, holder_t>::TrackProxy>> Fit implementation.
Note
The input measurements are given in the form of
SourceLinks. It’s the calibrators job to turn them into calibrated measurements used in the fit.- Template Parameters
source_link_iterator_t – Iterator type used to pass source links
start_parameters_t – Type of the initial parameters
parameters_t – Type of parameters used for local parameters
track_container_t – Type of the track container backend
holder_t – Type defining track container backend ownership
- Parameters
it – Begin iterator for the fittable uncalibrated measurements
end – End iterator for the fittable uncalibrated measurements
sParameters – The initial track parameters
gx2fOptions – Gx2FitterOptions steering the fit
trackContainer – Input track container storage to append into
- Returns
the output as an output track
-
template<typename traj_t>
struct Gx2FitterExtensions - #include <Acts/TrackFitting/GlobalChiSquareFitter.hpp>
Extension struct which holds delegates to customize the KF behavior.
Public Types
-
using Calibrator = Delegate<void(const GeometryContext&, const CalibrationContext&, const SourceLink&, TrackStateProxy)>
-
using ConstTrackStateProxy = typename MultiTrajectory<traj_t>::ConstTrackStateProxy
-
using OutlierFinder = Delegate<bool(ConstTrackStateProxy)>
-
using Parameters = typename TrackStateProxy::Parameters
-
using TrackStateProxy = typename MultiTrajectory<traj_t>::TrackStateProxy
-
using Updater = Delegate<Result<void>(const GeometryContext&, TrackStateProxy, Direction, const Logger&)>
Public Functions
-
inline Gx2FitterExtensions()
Default constructor which connects the default void components.
Public Members
-
Calibrator calibrator
The Calibrator is a dedicated calibration algorithm that allows to calibrate measurements using track information, this could be e.g.
sagging for wires, module deformations, etc.
-
OutlierFinder outlierFinder
Determines whether a measurement is supposed to be considered as an outlier.
-
SourceLinkSurfaceAccessor surfaceAccessor
Retrieves the associated surface from a source link.
-
Updater updater
The updater incorporates measurement information into the track parameters.
-
using Calibrator = Delegate<void(const GeometryContext&, const CalibrationContext&, const SourceLink&, TrackStateProxy)>
-
template<typename traj_t>
struct Gx2FitterOptions - #include <Acts/TrackFitting/GlobalChiSquareFitter.hpp>
Combined options for the Global-Chi-Square fitter.
- Template Parameters
traj_t – The trajectory type
Public Functions
-
Gx2FitterOptions() = delete
Contexts are required and the options must not be default-constructible.
-
inline Gx2FitterOptions(const GeometryContext &gctx, const MagneticFieldContext &mctx, std::reference_wrapper<const CalibrationContext> cctx, Gx2FitterExtensions<traj_t> extensions_, const PropagatorPlainOptions &pOptions, const Surface *rSurface = nullptr, bool mScattering = false, bool eLoss = false, const FreeToBoundCorrection &freeToBoundCorrection_ = FreeToBoundCorrection(false), const size_t nUpdateMax_ = 5)
PropagatorOptions with context.
- Parameters
gctx – The geometry context for this fit
mctx – The magnetic context for this fit
cctx – The calibration context for this fit
extensions_ – The KF extensions
pOptions – The plain propagator options
rSurface – The reference surface for the fit to be expressed at
mScattering – Whether to include multiple scattering
eLoss – Whether to include energy loss
freeToBoundCorrection_ – Correction for non-linearity effect during transform from free to bound
nUpdateMax_ – Max number of iterations for updating the parameters
Public Members
-
std::reference_wrapper<const CalibrationContext> calibrationContext
context object for the calibration
-
bool energyLoss = false
Whether to consider energy loss.
-
Gx2FitterExtensions<traj_t> extensions
-
FreeToBoundCorrection freeToBoundCorrection
Whether to include non-linear correction during global to local transformation.
-
std::reference_wrapper<const GeometryContext> geoContext
Context object for the geometry.
-
std::reference_wrapper<const MagneticFieldContext> magFieldContext
Context object for the magnetic field.
-
bool multipleScattering = false
Whether to consider multiple scattering.
-
size_t nUpdateMax = 5
Max number of iterations during the fit.
-
PropagatorPlainOptions propagatorPlainOptions
The trivial propagator options.
-
const Surface *referenceSurface = nullptr
The reference Surface.
-
template<typename traj_t>
struct Gx2FitterResult - #include <Acts/TrackFitting/GlobalChiSquareFitter.hpp>
Public Members
-
std::vector<ActsSquareMatrix<2>> collectorCovariance
-
std::vector<BoundMatrix> collectorJacobians
-
std::vector<ActsVector<2>> collectorResiduals
-
bool finished = false
-
std::optional<BoundTrackParameters> fittedParameters
-
traj_t *fittedStates = {nullptr}
-
BoundMatrix jacobianFromStart = BoundMatrix::Identity()
-
size_t lastMeasurementIndex = Acts::MultiTrajectoryTraits::kInvalid
-
size_t lastTrackIndex = Acts::MultiTrajectoryTraits::kInvalid
-
size_t measurementHoles = 0
-
size_t measurementStates = 0
-
std::vector<const Surface*> missedActiveSurfaces
-
std::vector<const Surface*> passedAgainSurfaces
-
size_t processedStates = 0
-
size_t surfaceCount = 0
-
std::vector<ActsSquareMatrix<2>> collectorCovariance
-
class IDetectorBuilder
- #include <Acts/Detector/interface/IDetectorBuilder.hpp>
This is the interface for building a Detector object.
This is the top level interface, all lower level building blocks should be done with detector component builders.
Note
As this is the last builder, the returned detector object is const and cannot be modified anymore.
Subclassed by Acts::Experimental::DetectorBuilder
Public Functions
-
virtual ~IDetectorBuilder() = default
-
virtual std::shared_ptr<const Detector> construct(const GeometryContext &gctx) const = 0
The virtual interface definition for detector builders.
- Parameters
gctx – the geometry context at the creation of the internal structure
- Returns
a shared detector object
-
virtual ~IDetectorBuilder() = default
-
class IDetectorComponentBuilder
- #include <Acts/Detector/interface/IDetectorComponentBuilder.hpp>
This is the interface for detector component builders; such a builder could be a simple detector volume builder, with or without internal structure, or more complicated objects.
Subclassed by Acts::Experimental::CylindricalContainerBuilder, Acts::Experimental::DetectorVolumeBuilder
Public Functions
-
virtual ~IDetectorComponentBuilder() = default
-
virtual DetectorComponent construct(const GeometryContext &gctx) const = 0
The interface method to be implemented by all detector component builder.
- Parameters
gctx – The geometry context for this call
- Returns
an outgoing detector component
-
virtual ~IDetectorComponentBuilder() = default
-
class IExternalStructureBuilder
- #include <Acts/Detector/interface/IExternalStructureBuilder.hpp>
This is the interface definition of external structure builders for DetectorVolume construction.
Subclassed by Acts::Experimental::VolumeStructureBuilder
Public Functions
-
virtual ~IExternalStructureBuilder() = default
-
virtual ExternalStructure construct(const GeometryContext &gctx) const = 0
The virtual interface definition for external structure creation.
- Parameters
gctx – the geometry context at the creation of the internal structure
- Returns
a consistent set of detector volume externals
-
virtual ~IExternalStructureBuilder() = default
-
class IInternalStructureBuilder
- #include <Acts/Detector/interface/IInternalStructureBuilder.hpp>
This is the interface definition of internal structure builders for DetectorVolume construction.
It is assumed that each builder returns a consistent set of DetectorVolume internals, which in turn can be directly provided to a DetectorVolume constructor.
Subclassed by Acts::Experimental::LayerStructureBuilder
Public Functions
-
virtual ~IInternalStructureBuilder() = default
-
virtual InternalStructure construct(const GeometryContext &gctx) const = 0
The interface definition for internal structure creation.
- Parameters
gctx – the geometry context at the creation of the internal structure
- Returns
a consistent set of detector volume internals
-
virtual ~IInternalStructureBuilder() = default
- #include <Acts/Navigation/NavigationDelegates.hpp>
Base class for navigation delegates This allows to define a common Owning delegate schema, which in turn allows for accessing the holder of the delegate implementation for e.g.
I/O or display
Subclassed by Acts::Experimental::IndexedUpdatorImpl< VariableBoundIndexGrid1, DetectorVolumesCollection, DetectorVolumeFiller >, Acts::Experimental::AdditionalSurfacesImpl, Acts::Experimental::AllPortalsAndSurfacesImpl, Acts::Experimental::AllPortalsImpl, Acts::Experimental::BoundVolumesGrid1Impl, Acts::Experimental::ChainedUpdatorImpl< updators_t >, Acts::Experimental::EndOfWorldImpl, Acts::Experimental::IndexedUpdatorImpl< grid_t, extractor_type, filler_type >, Acts::Experimental::NoopFinder, Acts::Experimental::RootVolumeFinder, Acts::Experimental::SingleDetectorVolumeImpl, Acts::Experimental::SingleObjectImpl< object_type, filler_type >, Acts::Experimental::StaticUpdatorImpl< extractor_type, filler_type >, Acts::Experimental::TrialAndErrorVolumeFinder
Public Functions
-
struct IndexedDetectorVolumeExtractor
- #include <Acts/Navigation/DetectorVolumeFinders.hpp>
A helper struct that allows to extrace a volume from the detector by its index.
Public Static Functions
Extract the surfaces from the volume.
- Parameters
gctx – the geometry contextfor this extraction call
nState – is the current navigation state
index – is the index in the global detector volume store
- Returns
a raw DetectorVolume pointer
-
struct IndexedSubVolumesExtractor
- #include <Acts/Detector/DetectorVolume.hpp>
Helper extractors: indexed sub volume of a volume.
Public Static Functions
Extract the sub volumes from the volume.
- Parameters
gctx – the geometry contextfor this extraction call
nState – is the current navigation state
indices – are access indices into the volume store
- Returns
a vector of raw DetectorVolume pointers
-
struct IndexedSurfacesExtractor
- #include <Acts/Detector/DetectorVolume.hpp>
Helper extractors: indexed surfaces.
Public Static Functions
Extract the surfaces from the volume.
Note
no out of boudns checking is done
- Parameters
gctx – the geometry contextfor this extraction call
nState – is the current navigation state
indices – are access indices into the surfaces store
- Returns
a vector of raw Surface pointers
-
template<typename grid_t, typename extractor_type, typename filler_type>
class IndexedUpdatorImpl : public Acts::Experimental::INavigationDelegate - #include <Acts/Navigation/NavigationStateUpdators.hpp>
This is an index grid based navigation state updator, it uses an extractor type and a filler type to handle the navigation state.
It can be used for volumes, surfaces at convenience
Note
a transform is applied
p3l = transform * p3in order to allow shifted, transformed grids- Template Parameters
grid_t – is the type of the grid
extractor_type – is the helper to extract the object
filler_type – is the helper to fill the object into the nState
Public Types
-
using grid_type = grid_t
Broadcast the grid type.
Public Functions
-
IndexedUpdatorImpl() = delete
-
inline IndexedUpdatorImpl(grid_type &&igrid, const std::array<BinningValue, grid_type::DIM> &icasts, const Transform3 &itr = Transform3::Identity())
Constructor for a grid based surface attacher.
- Parameters
igrid – the grid that is moved into this attacher
icasts – is the cast values array
itr – a transform applied to the global position
-
inline std::array<ActsScalar, grid_type::DIM> castPosition(const Vector3 &position) const
Cast into a lookup position.
- Parameters
position – is the position of the update call
updates the navigation state with objects from the grid according to the filling type AFTER applying
p3loc = transform * p3Note
this is attaching objects without intersecting nor checking
- Parameters
gctx – is the Geometry context of this call
nState – the navigation state to which the surfaces are attached
Public Members
-
std::array<BinningValue, grid_type::DIM> casts = {}
These are the cast parameters - copied from constructor.
-
extractor_type extractor
An extractor helper to get the object(s) from the volume.
-
grid_type grid
The grid where the indices are stored.
-
Transform3 transform = Transform3::Identity()
A transform to be applied to the position.
-
struct InternalStructure
- #include <Acts/Detector/DetectorComponents.hpp>
Holder struct for the internal structure components of a DetectorVolume.
Note
the surface surfacesUpdator needs to handle also portal providing of contained volumes.
Public Members
-
std::vector<std::shared_ptr<Surface>> surfaces = {}
Contained surfaces of this volume, handled by the surfacesUpdator.
-
SurfaceCandidatesUpdator surfacesUpdator
Navigation delegate for surfaces.
-
std::vector<std::shared_ptr<DetectorVolume>> volumes = {}
Contained volumes of this volume, handled by the volumeUpdator.
-
DetectorVolumeUpdator volumeUpdator
-
std::vector<std::shared_ptr<Surface>> surfaces = {}
-
class ISurfacesProvider
- #include <Acts/Detector/interface/ISurfacesProvider.hpp>
This is the interface for providing surfaces to the detector building process.
These surfaces manly describe the sensitive detector surfaces, but also passive (i.e. material carrying) surfaces are considered.
These could be prefilled, or created on demand when the detector is built (to increase memory locality)
Subclassed by Acts::Experimental::KdtSurfacesProvider< kDIM, bSize, reference_generator >, Acts::Experimental::LayerStructureBuilder::SurfacesHolder
Public Functions
-
virtual ~ISurfacesProvider() = default
-
virtual std::vector<std::shared_ptr<Surface>> surfaces(const GeometryContext &gctx) const = 0
The virtual interface definition for detector surface providers.
- Parameters
gctx – the geometry context at the creation of the internal structure
- Returns
a shared detector object
-
virtual ~ISurfacesProvider() = default
-
template<size_t kDIM = 2u, size_t bSize = 100u, typename reference_generator = detail::PolyhedronReferenceGenerator>
class KdtSurfaces - #include <Acts/Detector/KdtSurfacesProvider.hpp>
A wrapper class around a KDTree of surfaces.
It also deals with the conversion from global query to KDTree lookup positions
Public Types
-
using KDTS = KDTree<kDIM, std::shared_ptr<Surface>, ActsScalar, std::array, bSize>
Broadcast the surface KDT type.
-
using Query = std::array<ActsScalar, kDIM>
Broadcast the query definition.
Public Functions
Constructor from a vector of surfaces.
- Parameters
gctx – the geometry context of this call
surfaces – the surfaces to be filled into the tree
casts – the cast list from global position into kdtree local
rgen – the reference point generator
-
inline std::vector<std::shared_ptr<Surface>> surfaces(const Extent &extent) const
Query with an Extent object.
- Parameters
extent – is the range Extent to be queried
- Returns
the matching surfaces fpulled from the KDT structure
-
inline std::vector<std::shared_ptr<Surface>> surfaces(const RangeXD<kDIM, ActsScalar> &range) const
Query with a Range object.
- Parameters
range – is the range to be queried
- Returns
the matching surfaces from the KDT structure
-
using KDTS = KDTree<kDIM, std::shared_ptr<Surface>, ActsScalar, std::array, bSize>
-
template<size_t kDIM = 2u, size_t bSize = 100u, typename reference_generator = detail::PolyhedronReferenceGenerator>
class KdtSurfacesProvider : public Acts::Experimental::ISurfacesProvider - #include <Acts/Detector/KdtSurfacesProvider.hpp>
Callable struct wrapper around the KDT surface structure.
This allows to create small region based callable structs at configuration level that are then connected to an InternalStructureBuilder
Public Functions
The prefilled surfaces in a KD tree structure, it is generally shared amongst different providers.
- Parameters
kdts – the prefilled KDTree structure
kregion – the region where these are pulled from
-
inline std::vector<std::shared_ptr<Surface>> surfaces([[maybe_unused]] const GeometryContext &gctx) const final
The call to provide the surfaces.
-
class LayerStructureBuilder : public Acts::Experimental::IInternalStructureBuilder
- #include <Acts/Detector/LayerStructureBuilder.hpp>
This is a builder of layer structures to be contained within a DetectorVolume, it extends the IInternalStructureBuilder interface and provides the internal structure components of DetectorVolume objects to be constructed.
It uses the IndexedSurfaceGrid to bin the internal surfaces, and allows for additional support surfaces that are added to the structure and indexing mechanism. Those support structures can also be approximated by planar surfaces, in order to facilitate vectorization of surface intersection calls.
The binning can be chosen with a so called
expansion, a number which indicates the configured expanded bin window in which the surfaces are going to be filled, the details to this strategy can be found in the IndexedGridFiller and IndexedSurfacesGenerator classes.No sub volumes are added to this structure builders, hence, the DetectorVolumeFinder navigation delegate uses the “NoopFinder” breakpoint to indicate the bottom of the volume hierarchy.
Public Functions
-
LayerStructureBuilder(const Config &cfg, std::unique_ptr<const Logger> logger = getDefaultLogger("LayerStructureBuilder", Logging::INFO))
Constructor.
- Parameters
cfg – is the configuration struct
logger – logging instance for screen output
-
virtual InternalStructure construct(const GeometryContext &gctx) const final
The interface definition for internal structure creation.
- Parameters
gctx – the geometry context at the creation of the internal structure
- Returns
a consistent set of detector volume internals
-
struct Config
- #include <Acts/Detector/LayerStructureBuilder.hpp>
Configuration struct for the LayerStructureBuilder.
It contain:
a source of the surfaces to be built
a definition of surface binning on this layer
a definition of supports to be built
Public Members
-
std::string auxiliary = ""
Extra information, mainly for screen output.
-
std::vector<ProtoBinning> binnings = {}
Definition of Binnings.
-
unsigned int nSegments = 1u
Polyhedron approximations.
-
std::vector<Support> supports = {}
Definition of Supports.
-
std::shared_ptr<ISurfacesProvider> surfacesProvider = nullptr
Connection point for a function to provide surfaces.
-
struct Support
- #include <Acts/Detector/LayerStructureBuilder.hpp>
Support parameter definitions.
Public Members
-
std::vector<BinningValue> constraints = s_binningValues
Define in which values the support should be constrained.
-
unsigned int splits = 1u
Potential splits into planar approximations.
-
std::optional<Transform3> transform = std::nullopt
The (optional) layer transform.
-
Surface::SurfaceType type = Surface::SurfaceType::Other
The surface type to be built.
-
std::array<ActsScalar, 5u> values = {}
Define whether you want to build support structures.
-
std::vector<BinningValue> constraints = s_binningValues
-
class SurfacesHolder : public Acts::Experimental::ISurfacesProvider
- #include <Acts/Detector/LayerStructureBuilder.hpp>
A holder struct for surfaces.
Public Functions
Constructor with predefined surfaces.
- Parameters
isurfaces – is the vector of surfaces
-
inline std::vector<std::shared_ptr<Surface>> surfaces([[maybe_unused]] const GeometryContext &gctx) const final
Return the surfaces from the holder.
- Parameters
gctx – is the geometry context
-
LayerStructureBuilder(const Config &cfg, std::unique_ptr<const Logger> logger = getDefaultLogger("LayerStructureBuilder", Logging::INFO))
- #include <Acts/Navigation/NavigationState.hpp>
A navigation state struct that is holding the current navigation information.
It relies on Surfaces and Portals, all navigation entities have to be described in these terms.
Subclassed by Acts::Experimental::DetectorNavigator::State
Public Types
Surface candidate vector alias, this allows to use e.g.
boost_small vector or other stl like containers
Public Members
The current absolute charge.
The current absolute momentum.
Auxiliary attached information.
The current detector in processing.
The current portal, i.e the position is on portal.
The current surface, i.e the position is on surface.
The current volume in processing, i.e. the position is inside.
The current direction.
The current magnetic field.
An overstep tolerance.
The current position.
Boundary directives for surfaces.
That are the candidate surfaces to process.
- #include <Acts/Navigation/NavigationState.hpp>
A surface candidate and its intersection.
A candidates can either be a surface or a portal (which contain a surface)
Public Members
The boundary check used for the candidate, boundary checks can differ for sensitive surfaces and portals.
A candidate intersection, in Surface view.
Or a portal.
A candidate is either a detector Surface.
-
struct NoopFinder : public Acts::Experimental::INavigationDelegate
- #include <Acts/Navigation/DetectorVolumeFinders.hpp>
Public Functions
-
class Portal : public std::enable_shared_from_this<Portal>
- #include <Acts/Detector/Portal.hpp>
A portal description between the detector volumes.
It has a Surface representation for navigation and propagation and guides from one volume to the next.
The surface can carry material to allow mapping onto portal positions if required.
Public Types
-
using AttachedDetectorVolumes = std::array<std::vector<std::shared_ptr<DetectorVolume>>, 2u>
The vector of attached volumes forward/backward, this is useful in the geometry building.
-
using DetectorVolumeUpdators = std::array<DetectorVolumeUpdator, 2u>
The volume links forward/backward with respect to the surface normal.
Public Functions
-
Portal() = delete
-
virtual ~Portal() = default
Update the volume link, w/o directive, i.e.
it relies that there’s only one remaining link to be set, throws an exception if that’s not the case
Note
this overwrites the existing link
- Parameters
dVolumeUpdator – is the mangaged volume updator delegate
attachedVolumes – is the list of attached volumes for book keeping
Update the volume link.
Note
this overwrites the existing link
- Parameters
dir – the direction of the link
dVolumeUpdator – is the mangaged volume updator delegate
attachedVolumes – is the list of attached volumes for book keeping
-
void assignGeometryId(const GeometryIdentifier &geometryId)
Set the geometry identifier (to the underlying surface)
- Parameters
geometryId – the geometry identifier to be assigned
-
AttachedDetectorVolumes &attachedDetectorVolumes()
-
const DetectorVolumeUpdators &detectorVolumeUpdators() const
Fuse with another portal, this one is kept.
Note
this will move the portal links from the other into this volume, it will throw an exception if the portals are not fusable
Note
that other will be overwritten to point to this
- Parameters
other – is the portal that will be fused
Retrieve a
std::shared_ptrfor this surface (non-const version)Note
Will error if this was not created through the
makeSharedfactory since it needs access to the original reference. In C++14 this is undefined behavior (but most likely implemented as abad_weak_ptrexception), in C++17 it is defined as that exception.Note
Only call this if you need shared ownership of this object.
- Returns
The shared pointer
Retrieve a
std::shared_ptrfor this surface (const version)Note
Will error if this was not created through the
makeSharedfactory since it needs access to the original reference. In C++14 this is undefined behavior, but most likely implemented as abad_weak_ptrexception, in C++17 it is defined as that exception.Note
Only call this if you need shared ownership of this object.
- Returns
The shared pointer
-
Surface &surface()
Non-const access to the surface reference.
-
const Surface &surface() const
Const access to the surface representation.
Update the current volume.
- Parameters
gctx – is the Geometry context of this call
nState – [in,out] the navigation state for the volume to be updated
Public Static Functions
Factory for producing memory managed instances of Portal.
Friends
- friend class DetectorVolume
-
using AttachedDetectorVolumes = std::array<std::vector<std::shared_ptr<DetectorVolume>>, 2u>
-
struct PortalsFiller
- #include <Acts/Navigation/NavigationStateFillers.hpp>
Fillers and attachers for portals to act on the navigation state.
Public Static Functions
Helper struct that allows to fill surfaces into the candidate vector it allows to use common navigation structs for volume, portal, surfaces.
- Parameters
nState – the navigation state
portals – the portals that are filled in
-
struct ProtoBinning
- #include <Acts/Detector/ProtoBinning.hpp>
Simple helper class to define a binning structure.
Note
no checks are performed on the consistency, this is only for convenience that the binning can be defined and then translated into concrete axis types
Public Functions
-
inline ProtoBinning(BinningValue bValue, Acts::detail::AxisBoundaryType bType, ActsScalar minE, ActsScalar maxE, std::size_t nbins, std::size_t exp = 0u)
Convenience constructors - recommended for variable binning.
- Parameters
bValue – the value/cast in which this is binned
bType – the axis boundary type
minE – the lowest edge of the binning
maxE – the highest edge of the binning
nbins – the number of bins
exp – the expansion (in bins)
-
inline ProtoBinning(BinningValue bValue, Acts::detail::AxisBoundaryType bType, const std::vector<ActsScalar> &e, std::size_t exp = 0u)
Convenience constructors - recommended for variable binning.
- Parameters
bValue – the value/cast in which this is binned
bType – the axis boundary type
e – the bin edges (variable binning)
exp – the expansion (in bins)
-
inline std::size_t bins() const
Public Members
-
Acts::detail::AxisType axisType = Acts::detail::AxisType::Equidistant
The axis type: equidistant or variable.
-
BinningValue binValue = BinningValue::binValues
The binning value of this.
-
Acts::detail::AxisBoundaryType boundaryType = Acts::detail::AxisBoundaryType::Bound
The axis boundary type: Open, Bound or Closed.
-
std::vector<ActsScalar> edges = {}
The binning edges.
-
std::size_t expansion = 0u
An expansion for the filling (in bins)
-
inline ProtoBinning(BinningValue bValue, Acts::detail::AxisBoundaryType bType, ActsScalar minE, ActsScalar maxE, std::size_t nbins, std::size_t exp = 0u)
-
struct RootDetectorVolumes
- #include <Acts/Detector/DetectorComponents.hpp>
Container to collect root volumes for the construction of a Detector.
This struct collects all root volumes that will then be provided to the Detector object
Note
each root volume is expected to contain a full search tree for eventually contained sub volumes
Public Members
-
DetectorVolumeUpdator volumeFinder
The Root volumes finder.
-
std::vector<std::shared_ptr<DetectorVolume>> volumes = {}
The list of root volumes.
-
DetectorVolumeUpdator volumeFinder
-
struct RootVolumeFinder : public Acts::Experimental::INavigationDelegate
- #include <Acts/Navigation/DetectorVolumeFinders.hpp>
Public Functions
-
struct SingleDetectorVolumeImpl : public Acts::Experimental::INavigationDelegate
- #include <Acts/Navigation/DetectorVolumeUpdators.hpp>
Single volume updator, it sets the current navigation volume to the volume in question.
Public Functions
-
SingleDetectorVolumeImpl() = delete
-
inline SingleDetectorVolumeImpl(const DetectorVolume *sVolume) noexcept(false)
Allowed constructor.
- Parameters
sVolume – the volume to which it points
a null volume link - explicitly
Note
the method parameters are ignored
Public Members
-
const DetectorVolume *dVolume = nullptr
-
SingleDetectorVolumeImpl() = delete
-
template<typename object_type, typename filler_type>
class SingleObjectImpl : public Acts::Experimental::INavigationDelegate - #include <Acts/Navigation/NavigationStateUpdators.hpp>
This sets a single object, e.g.
single surface or single volume
- Template Parameters
object_type – the type of the object to be filled
filler_type – is the helper to fill the object into nState
Public Functions
-
inline SingleObjectImpl(const object_type *so)
Convenience constructor.
- Parameters
so – the single object
updates the navigation state with a single object that is filled in
Note
this is attaching objects without intersecting nor checking
- Parameters
gctx – is the Geometry context of this call
nState – the navigation state to which the surfaces are attached
-
template<typename extractor_type, typename filler_type>
class StaticUpdatorImpl : public Acts::Experimental::INavigationDelegate - #include <Acts/Navigation/NavigationStateUpdators.hpp>
This uses state less extractor and fillers to manipulate the navigation state.
- Template Parameters
extractor_type – the helper to extract the objects from
filler_type – is the helper to fill the object into nState
Public Functions
updates the navigation state with a single object that is filled in
Note
this is attaching objects without intersecting nor checking
- Parameters
gctx – is the Geometry context of this call
nState – the navigation state to which the surfaces are attached
-
struct SurfacesFiller
- #include <Acts/Navigation/NavigationStateFillers.hpp>
Fillers and attachers for surfaces to act on the navigation state.
Public Static Functions
Helper struct that allows to fill surfaces into the candidate vector it allows to use common navigation structs for volume, portal, surfaces.
- Parameters
nState – the navigation state
surfaces – the surfaces that are filled in
-
struct TrialAndErrorVolumeFinder : public Acts::Experimental::INavigationDelegate
- #include <Acts/Navigation/DetectorVolumeFinders.hpp>
Public Functions
-
class VolumeStructureBuilder : public Acts::Experimental::IExternalStructureBuilder
- #include <Acts/Detector/VolumeStructureBuilder.hpp>
This class provides the external detector volume structure, configured either from:
a volume extent
from an array with volume bounds identification
Note
A starting transform (defaulted to identity) can be provided, in case of volume bounds construction from an
Acts::Extentobject, the transform steming from the extent definition will be applied on top of the provided starting transform. In case of volume bounds construction from an array of values, the starting transform is already the final volume placement.Public Functions
-
VolumeStructureBuilder(const Config &cfg, std::unique_ptr<const Logger> mlogger = getDefaultLogger("VolumeStructureBuilder", Logging::INFO))
Constructor.
- Parameters
cfg – is the configuration struct
mlogger – logging instance for screen output
-
virtual ExternalStructure construct(const GeometryContext &gctx) const final
The interface definition for internal structure creation.
- Parameters
gctx – the geometry context at the creation of the internal structure
- Returns
a consistent set of detector volume internals
-
struct Config
- #include <Acts/Detector/VolumeStructureBuilder.hpp>
Nexted configuration struct.
Public Members
-
std::string auxiliary = ""
Some auxiliary information.
-
VolumeBounds::BoundsType boundsType = VolumeBounds::BoundsType::eOther
A defined volume bound type.
-
std::vector<ActsScalar> boundValues = {}
The values (if already defined)
-
std::optional<Extent> extent = std::nullopt
The optional extent to feed into the values.
-
Transform3 transform = Transform3::Identity()
The starting transform.
-
std::string auxiliary = ""
-
namespace GsfConstants
Typedefs
-
using FinalMultiComponentState = std::optional<Acts::MultiComponentBoundTrackParameters<SinglyCharged>>
Variables
-
constexpr std::string_view kFinalMultiComponentStateColumn = "gsf-final-multi-component-state"
-
using FinalMultiComponentState = std::optional<Acts::MultiComponentBoundTrackParameters<SinglyCharged>>
-
using DetectorBlock = std::tuple<DetectorVolumes, ProtoContainer>
-
namespace GridJsonConverter
Functions
-
template<typename axis_generator_type>
auto fromJson(const nlohmann::json &jGrid, const axis_generator_type &aGenerator) Templated grid conversion from json.
Note
the axis generator also defines the grid dimension
- Template Parameters
axis_generator_type – the type of the axis generator which determines the grid type
- Parameters
jGrid – the json object to represent the grid
aGenerator – the axis generator
- Returns
a grid object
-
template<typename grid_type>
nlohmann::json toJson(const grid_type &grid) Templated grid conversion to json.
- Template Parameters
grid_type – the type of the grid
- Parameters
grid – the grid object
- Returns
a json object to represent the grid
-
template<typename axis_generator_type>
-
namespace HashedStringLiteral
Functions
-
constexpr HashedString operator""_hash(char const *s, std::size_t count)
-
constexpr HashedString operator""_hash(char const *s, std::size_t count)
-
namespace IndexedSurfacesJsonConverter
Functions
-
template<typename instance_type>
void convert(nlohmann::json &jIndexedSurfaces, const Experimental::SurfaceCandidatesUpdator &delegate, [[maybe_unused]] const instance_type &refInstance) Convert the single delegate if it is of the type of the reference.
Note
It will do nothing if the type does not match
- Parameters
jIndexedSurfaces – the json object to be filled
delegate – the delegate to be translated
refInstance – is a reference instance of potential type casting
-
template<typename index_grid>
nlohmann::json convertImpl(const index_grid &indexGrid) The actual conversion method.
-
Experimental::SurfaceCandidatesUpdator fromJson(const nlohmann::json &jSurfaceNavigation)
Convert the single delegate if it is of the type of the reference.
- Parameters
jSurfaceNavigation – the json file to read from
- Returns
the surface navigation delegate
-
static inline nlohmann::json toJson(const Experimental::SurfaceCandidatesUpdator &delegate)
Convert a surface array into needed constituents.
Note
this is the entry point of the conversion, i.e. top of the unrolling loop
- Parameters
delegate – the delegate to be translated
- Returns
a collection of proto surface object and a grid, and associations
-
template<typename tuple_type, std::size_t... I>
void unrollConvert(nlohmann::json &jIndexedSurfaces, const Experimental::SurfaceCandidatesUpdator &delegate, const tuple_type &axesTuple, std::index_sequence<I...>) Unrolling function for catching the right instance.
Note
parameters are as of the
convertImplmethod- Parameters
jIndexedSurfaces – the json object to be filled
delegate – the delegate to be translated
axesTuple – the tuple of axes to be unrolled
Variables
-
static auto s_possibleAxes = std::tuple<EqBound, EqOpen, EqClosed, VarBound, VarOpen, VarClosed, EqBoundEqBound, EqBoundEqOpen, EqBoundEqClosed, EqOpenEqBound, EqOpenEqOpen, EqOpenEqClosed, EqClosedEqBound, EqClosedEqOpen, EqClosedEqClosed, EqBoundVarBound, EqBoundVarOpen, EqBoundVarClosed, EqOpenVarBound, EqOpenVarOpen, EqOpenVarClosed, EqClosedVarBound, EqClosedVarOpen, EqClosedVarClosed, VarBoundEqBound, VarBoundEqOpen, VarBoundEqClosed, VarOpenEqBound, VarOpenEqOpen, VarOpenEqClosed, VarClosedEqBound, VarClosedEqOpen, VarClosedEqClosed, VarBoundVarBound, VarBoundVarOpen, VarBoundVarClosed, VarOpenVarBound, VarOpenVarOpen, VarOpenVarClosed, VarClosedVarBound, VarClosedVarOpen, VarClosedVarClosed>{}
-
template<typename instance_type>
-
namespace KalmanVertexTrackUpdater
Functions
-
template<typename input_track_t>
void update(TrackAtVertex<input_track_t> &track, const Vertex<input_track_t> &vtx) KalmanVertexTrackUpdater.
Refits a single track with the knowledge of the vertex it has originated from
- Parameters
track – Track to update
vtx – Vertex
trackbelongs to
-
template<typename input_track_t>
-
namespace KalmanVertexUpdater
Functions
-
template<typename input_track_t>
void updatePosition(const Acts::Vertex<input_track_t> &vtx, const Acts::LinearizedTrack &linTrack, double trackWeight, int sign, MatrixCache &matrixCache) Updates vertex position.
- Parameters
vtx – Old vertex
linTrack – Linearized version of track to be added or removed
trackWeight – Track weight
sign – +1 (add track) or -1 (remove track)
matrixCache – [out] A cache to store matrix information
-
template<typename input_track_t>
void updateVertexWithTrack(Vertex<input_track_t> &vtx, TrackAtVertex<input_track_t> &trk) Updates vertex with knowledge of new track.
Note
KalmanVertexUpdater updates the vertex w.r.t. the newly given track, but does NOT add the track to the TrackAtVertex list. Has to be done manually after calling this method
- Parameters
vtx – Vertex to be updated
trk – Track to be used for updating the vertex
-
struct MatrixCache
- #include <Acts/Vertexing/KalmanVertexUpdater.hpp>
KalmanVertexUpdater.
adds or removes track from or updates current vertex Based on R. Frühwirth et al. Vertex reconstruction and track bundling at the lep collider using robust Algorithms Computer Physics Comm.: 96 (1996) 189, chapter 2.1 Cache object to store matrix information
Public Members
-
SquareMatrix3 momWeightInv = SquareMatrix3::Zero()
-
SquareMatrix3 newVertexCov = SquareMatrix3::Zero()
-
SquareMatrix3 newVertexWeight = SquareMatrix3::Zero()
-
SquareMatrix3 oldVertexWeight = SquareMatrix3::Zero()
-
SquareMatrix3 momWeightInv = SquareMatrix3::Zero()
-
template<typename input_track_t>
-
namespace Legacy
-
template<typename SpacePoint>
class AtlasSeedFinder - #include <Acts/Seeding/AtlasSeedFinder.hpp>
Public Functions
-
AtlasSeedFinder()
-
inline virtual ~AtlasSeedFinder()
-
void find3Sp()
-
inline const Seed<SpacePoint> *next()
Public Members
-
const Config m_config
-
AtlasSeedFinder()
-
class comCurvature
- #include <Acts/Seeding/AtlasSeedFinder.hpp>
Public Functions
-
template<typename SpacePoint>
inline bool operator()(const std::pair<float, Acts::Legacy::SPForSeed<SpacePoint>*> &i1, const std::pair<float, Acts::Legacy::SPForSeed<SpacePoint>*> &i2)
-
template<typename SpacePoint>
-
template<typename SpacePoint>
class InternalSeed - #include <Acts/Seeding/LegacyInternalSeed.hpp>
Public Functions
-
InternalSeed()
-
InternalSeed(const InternalSeed<SpacePoint>&)
-
InternalSeed(SPForSeed<SpacePoint>*&, SPForSeed<SpacePoint>*&, SPForSeed<SpacePoint>*&, float)
-
virtual ~InternalSeed()
-
InternalSeed<SpacePoint> &operator=(const InternalSeed<SpacePoint>&)
-
inline const float &quality() const
-
void set(SPForSeed<SpacePoint>*&, SPForSeed<SpacePoint>*&, SPForSeed<SpacePoint>*&, float)
-
bool set3(Acts::Legacy::Seed<SpacePoint>&)
-
bool setQuality(float)
-
inline SPForSeed<SpacePoint> *spacepoint0()
-
inline SPForSeed<SpacePoint> *spacepoint1()
-
inline SPForSeed<SpacePoint> *spacepoint2()
-
inline const float &z() const
-
InternalSeed()
-
template<typename SpacePoint>
class Seed - #include <Acts/Seeding/LegacySeed.hpp>
Public Functions
-
Seed()
-
Seed(const Seed&)
-
Seed(const SpacePoint*, const SpacePoint*, const SpacePoint*, const double)
-
virtual ~Seed()
-
void add(const SpacePoint*&)
-
void erase()
-
void setZVertex(const double&)
-
const std::list<const SpacePoint*> &spacePoints() const
-
const double &zVertex() const
-
Seed()
-
template<typename SpacePoint>
class SPForSeed - #include <Acts/Seeding/SPForSeed.hpp>
Public Functions
-
inline SPForSeed()
-
inline SPForSeed(const SPForSeed&)
-
inline SPForSeed(SpacePoint*const&, const float*)
-
inline SPForSeed(SpacePoint*const&, const float*, const float*)
-
inline virtual ~SPForSeed()
-
inline const float &covr() const
-
inline const float &covz() const
-
inline const float ¶m() const
-
inline float phi() const
-
inline const float &quality() const
-
inline const float &radius() const
-
inline void set(SpacePoint*const&, const float*)
-
inline void set(SpacePoint*const&, const float*, const float*)
-
inline void setParam(const float&)
-
inline void setQuality(float)
-
inline const int &surface() const
-
inline const float &x() const
-
inline const float &y() const
-
inline const float &z() const
Public Members
-
const SpacePoint *spacepoint = nullptr
-
inline SPForSeed()
-
template<typename SpacePoint>
-
namespace Logging
debug output related helper classes and functions
Enums
-
enum Level
constants steering the debug output
All messages with a debug level equal or higher than the currently set debug output level will be printed.
Values:
-
enumerator VERBOSE
VERBOSE level.
-
enumerator DEBUG
DEBUG level.
-
enumerator INFO
INFO level.
-
enumerator WARNING
WARNING level.
-
enumerator ERROR
ERROR level.
-
enumerator FATAL
FATAL level.
-
enumerator MAX
Must be kept above the maximum supported debug level.
-
enumerator VERBOSE
Functions
-
Level getFailureThreshold()
Get debug level above which an exception will be thrown after logging.
All messages with a debug level equal or higher than the return value of this function will cause an exception to be thrown after log emission.
Note
Depending on preprocessor settings
ACTS_ENABLE_LOG_FAILURE_THRESHOLDandACTS_LOG_FAILURE_THRESHOLD, this operations is either constexpr or a runtime operation.
-
inline std::string_view levelName(Level level)
-
void setFailureThreshold(Level level)
Set debug level above which an exception will be thrown after logging.
All messages with a debug level equal or higher than
levelwill cause an exception to be thrown after log emission.Note
This function is only available if
ACTS_LOG_FAILURE_THRESHOLDis unset, i.e. no compile-time threshold is used. Otherwise an exception is thrown.Warning
The runtime log failure threshold is global state, therefore this function is not threadsafe. The intention is that this level is set once, before multi-threaded execution begins, and then not modified before the end of the job.
-
class DefaultFilterPolicy : public Acts::Logging::OutputFilterPolicy
- #include <Acts/Utilities/Logger.hpp>
default filter policy for debug messages
All debug messages with a debug level equal or larger to the specified threshold level are processed.
Public Functions
-
inline explicit DefaultFilterPolicy(Level lvl)
constructor
- Parameters
lvl – [in] threshold debug level
-
~DefaultFilterPolicy() override = default
virtual default destructor
-
inline virtual std::unique_ptr<OutputFilterPolicy> clone(Level level) const override
Make a copy of this filter policy with a new level.
- Parameters
level – the new level
- Returns
the new copy
-
inline virtual bool doPrint(const Level &lvl) const override
decide whether a debug message should be processed
- Parameters
lvl – [in] debug level of debug message
- Returns
trueiflvl>= m_level, otherwisefalse
-
inline virtual Level level() const override
Get the level of this filter policy.
- Returns
the levele
-
inline explicit DefaultFilterPolicy(Level lvl)
-
class DefaultPrintPolicy : public Acts::Logging::OutputPrintPolicy
- #include <Acts/Utilities/Logger.hpp>
default print policy for debug messages
This class allows to print debug messages without further modifications to a specified output stream.
Public Functions
-
inline explicit DefaultPrintPolicy(std::ostream *out = &std::cout)
constructor
- Parameters
out – [in] pointer to output stream object
- Pre
outis non-zero
-
inline virtual std::unique_ptr<OutputPrintPolicy> clone(const std::string &name) const override
Make a copy of this print policy with a new name.
- Parameters
name – the new name
- Returns
the copy
-
inline virtual void flush(const Level &lvl, const std::string &input) final
flush the debug message to the destination stream
- Parameters
lvl – [in] debug level of debug message
input – [in] text of debug message
-
inline virtual const std::string &name() const override
Fulfill
OutputPrintPolicyinterface.This policy doesn’t actually have a name, so the assumption is that somewhere in the decorator hierarchy, there is something that returns a name without delegating to a wrappee, before reaching this overload.
Note
This method will throw an exception
- Returns
the name, but it never returns
-
inline explicit DefaultPrintPolicy(std::ostream *out = &std::cout)
-
class LevelOutputDecorator : public Acts::Logging::OutputDecorator
- #include <Acts/Utilities/Logger.hpp>
decorate debug message with its debug level
The debug message is complemented with its debug level.
Public Functions
-
inline explicit LevelOutputDecorator(std::unique_ptr<OutputPrintPolicy> wrappee)
constructor
- Parameters
wrappee – [in] output print policy object to be wrapped
-
inline virtual std::unique_ptr<OutputPrintPolicy> clone(const std::string &name) const override
Make a copy of this print policy with a new name.
- Parameters
name – the new name
- Returns
the copy
-
inline virtual void flush(const Level &lvl, const std::string &input) override
flush the debug message to the destination stream
This function prepends the debug level to the debug message and then delegates the flushing of the whole message to its wrapped object.
- Parameters
lvl – [in] debug level of debug message
input – [in] text of debug message
-
inline explicit LevelOutputDecorator(std::unique_ptr<OutputPrintPolicy> wrappee)
-
class NamedOutputDecorator : public Acts::Logging::OutputDecorator
- #include <Acts/Utilities/Logger.hpp>
decorate debug message with a name
The debug message is complemented with a name.
Public Functions
-
inline NamedOutputDecorator(std::unique_ptr<OutputPrintPolicy> wrappee, const std::string &name, unsigned int maxWidth = 15)
constructor
- Parameters
wrappee – [in] output print policy object to be wrapped
name – [in] name to be added to debug message
maxWidth – [in] maximum width of field used for name
-
inline virtual std::unique_ptr<OutputPrintPolicy> clone(const std::string &name) const override
Make a copy of this print policy with a new name.
- Parameters
name – the new name
- Returns
the copy
-
inline virtual void flush(const Level &lvl, const std::string &input) override
flush the debug message to the destination stream
This function prepends the given name to the debug message and then delegates the flushing of the whole message to its wrapped object.
- Parameters
lvl – [in] debug level of debug message
input – [in] text of debug message
-
inline virtual const std::string &name() const override
Get this named output decorators name.
- Returns
the name
-
inline NamedOutputDecorator(std::unique_ptr<OutputPrintPolicy> wrappee, const std::string &name, unsigned int maxWidth = 15)
-
class OutputDecorator : public Acts::Logging::OutputPrintPolicy
- #include <Acts/Utilities/Logger.hpp>
base class for decorating the debug output
Derived classes may augment the debug message with additional information. Chaining different decorators is possible to customize the output to your needs.
Subclassed by Acts::Logging::LevelOutputDecorator, Acts::Logging::NamedOutputDecorator, Acts::Logging::ThreadOutputDecorator, Acts::Logging::TimedOutputDecorator
Public Functions
-
inline explicit OutputDecorator(std::unique_ptr<OutputPrintPolicy> wrappee)
constructor wrapping actual output print policy
- Parameters
wrappee – [in] output print policy object which is wrapped by this decorator object
-
inline virtual void flush(const Level &lvl, const std::string &input) override
flush the debug message to the destination stream
This function delegates the flushing of the debug message to its wrapped object.
- Parameters
lvl – [in] debug level of debug message
input – [in] text of debug message
-
inline virtual const std::string &name() const override
Return the name of the output decorator (forwards to wrappee)
- Returns
the name
-
inline explicit OutputDecorator(std::unique_ptr<OutputPrintPolicy> wrappee)
-
class OutputFilterPolicy
- #include <Acts/Utilities/Logger.hpp>
abstract base class for filtering debug output
Implementations of this interface need to define whether a debug message with a certain debug level is processed or filtered out.
Subclassed by Acts::Logging::DefaultFilterPolicy
Public Functions
-
virtual ~OutputFilterPolicy() = default
virtual default destructor
-
virtual std::unique_ptr<OutputFilterPolicy> clone(Level level) const = 0
Make a copy of this filter policy with a new level.
- Parameters
level – the new level
- Returns
the new copy
-
virtual bool doPrint(const Level &lvl) const = 0
decide whether a debug message should be processed
- Parameters
lvl – [in] debug level of debug message
- Returns
trueof debug message should be processed,falseif debug message should be skipped
-
virtual Level level() const = 0
Get the level of this filter policy.
- Returns
the levele
-
virtual ~OutputFilterPolicy() = default
-
class OutputPrintPolicy
- #include <Acts/Utilities/Logger.hpp>
abstract base class for printing debug output
Implementations of this interface need to define how and where to print debug messages (e.g. to a file, to a stream into a database etc).
Subclassed by Acts::Logging::DefaultPrintPolicy, Acts::Logging::OutputDecorator
Public Functions
-
virtual ~OutputPrintPolicy() = default
virtual default destructor
-
virtual std::unique_ptr<OutputPrintPolicy> clone(const std::string &name) const = 0
Make a copy of this print policy with a new name.
- Parameters
name – the new name
- Returns
the copy
-
virtual void flush(const Level &lvl, const std::string &input) = 0
handle output of debug message
- Parameters
lvl – [in] debug output level of message
input – [in] text of debug message
-
virtual const std::string &name() const = 0
Return the name of the print policy.
- Returns
the name
-
virtual ~OutputPrintPolicy() = default
-
class ThreadOutputDecorator : public Acts::Logging::OutputDecorator
- #include <Acts/Utilities/Logger.hpp>
decorate debug message with a thread ID
The debug message is complemented with a thread ID.
Public Functions
-
inline explicit ThreadOutputDecorator(std::unique_ptr<OutputPrintPolicy> wrappee)
constructor
- Parameters
wrappee – [in] output print policy object to be wrapped
-
inline virtual std::unique_ptr<OutputPrintPolicy> clone(const std::string &name) const override
Make a copy of this print policy with a new name.
- Parameters
name – the new name
- Returns
the copy
-
inline virtual void flush(const Level &lvl, const std::string &input) override
flush the debug message to the destination stream
This function prepends the thread ID to the debug message and then delegates the flushing of the whole message to its wrapped object.
- Parameters
lvl – [in] debug level of debug message
input – [in] text of debug message
-
inline explicit ThreadOutputDecorator(std::unique_ptr<OutputPrintPolicy> wrappee)
-
class ThresholdFailure : public std::runtime_error
- #include <Acts/Utilities/Logger.hpp>
Custom exception class so threshold failures can be caught.
-
class TimedOutputDecorator : public Acts::Logging::OutputDecorator
- #include <Acts/Utilities/Logger.hpp>
decorate debug message with a time stamp
The debug message is complemented with a time stamp.
Public Functions
-
inline TimedOutputDecorator(std::unique_ptr<OutputPrintPolicy> wrappee, const std::string &format = "%X")
constructor
- Parameters
wrappee – [in] output print policy object to be wrapped
format – [in] format of time stamp (see std::strftime)
-
inline virtual std::unique_ptr<OutputPrintPolicy> clone(const std::string &name) const override
Make a copy of this print policy with a new name.
- Parameters
name – the new name
- Returns
the copy
-
inline virtual void flush(const Level &lvl, const std::string &input) override
flush the debug message to the destination stream
This function prepends a time stamp to the debug message and then delegates the flushing of the whole message to its wrapped object.
- Parameters
lvl – [in] debug level of debug message
input – [in] text of debug message
-
inline TimedOutputDecorator(std::unique_ptr<OutputPrintPolicy> wrappee, const std::string &format = "%X")
-
enum Level
-
namespace MultiTrajectoryHelpers
Typedefs
-
using VolumeTrajectoryStateContainer = std::unordered_map<GeometryIdentifier::Value, TrajectoryState>
Functions
-
template<typename track_state_proxy_t>
FreeVector freeFiltered(const GeometryContext &gctx, const track_state_proxy_t &trackStateProxy) Transforms the filtered parameters from a
TrackStateProxyto free parameters.- Template Parameters
track_state_proxy_t – Type of the
TrackStateProxy- Parameters
gctx – [in] Geometry context
trackStateProxy – [in] TrackStateProxy
- Returns
Free parameters representation of the filtered parameters
-
template<typename track_state_proxy_t>
FreeVector freeSmoothed(const GeometryContext &gctx, const track_state_proxy_t &trackStateProxy) Transforms the smoothed parameters from a
TrackStateProxyto free parameters.- Template Parameters
track_state_proxy_t – Type of the
TrackStateProxy- Parameters
gctx – [in] Geometry context
trackStateProxy – [in] TrackStateProxy
- Returns
Free parameters representation of the smoothed parameters
-
template<typename traj_t>
TrajectoryState trajectoryState(const traj_t &multiTraj, size_t entryIndex) Getter for global trajectory info.
- Parameters
multiTraj – The MultiTrajectory object
entryIndex – The entry index of trajectory to investigate
- Returns
The trajectory summary info
-
template<typename traj_t>
VolumeTrajectoryStateContainer trajectoryState(const traj_t &multiTraj, size_t entryIndex, const std::vector<GeometryIdentifier::Value> &volumeIds) Getter for trajectory info for different sub-detectors.
- Template Parameters
source_link_t – Type of source link
- Parameters
multiTraj – The MultiTrajectory object
entryIndex – The entry index of trajectory to investigate track states at different sub-detectors.
volumeIds – The container for sub-detector Ids
- Returns
The trajectory summary info at different sub-detectors (i.e. different volumes)
-
struct TrajectoryState
- #include <Acts/EventData/MultiTrajectoryHelpers.hpp>
Struct for brief trajectory summary info.
Public Members
-
double chi2Sum = 0
-
std::vector<double> measurementChi2 = {}
-
std::vector<unsigned int> measurementLayer = {}
-
std::vector<unsigned int> measurementVolume = {}
-
size_t NDF = 0
-
size_t nHoles = 0
-
size_t nMeasurements = 0
-
size_t nOutliers = 0
-
size_t nStates = 0
-
std::vector<double> outlierChi2 = {}
-
std::vector<unsigned int> outlierLayer = {}
-
std::vector<unsigned int> outlierVolume = {}
-
double chi2Sum = 0
-
using VolumeTrajectoryStateContainer = std::unordered_map<GeometryIdentifier::Value, TrajectoryState>
-
namespace MultiTrajectoryTraits
This namespace contains typedefs and constant values that are used by other parts of the
MultiTrajectoryimplementation.It extracts these from
TrackStateTraitsusing the default maximum measurement dimension.Typedefs
-
using IndexType = TrackIndexType
Variables
-
constexpr IndexType kInvalid = kTrackIndexInvalid
-
constexpr unsigned int MeasurementSizeMax = eBoundSize
-
using IndexType = TrackIndexType
-
namespace PhysicalConstants
Physical constants in native units.
Unit constants are intentionally not listed.
Variables
-
constexpr double c = 1.0
-
constexpr double hbar = 6.582119569509066e-25 * UnitConstants::GeV * UnitConstants::s
Reduced Planck constant h/2*pi.
Computed from CODATA 2018 constants to double precision.
-
constexpr double c = 1.0
-
namespace PortalJsonConverter
Functions
convert from json format
- Parameters
gctx – the geometry context
jPortal – is the json portal description
detectorVolumes – is the list of already created detector volumes
- Returns
a Portal
-
nlohmann::json toJson(const Experimental::DetectorVolumeUpdator &updator, const std::vector<const Experimental::DetectorVolume*> &detectorVolumes)
convert to json format
- Parameters
updator – the detector volume updator
detectorVolumes – the list of all detector volumes
- Returns
a json object
-
nlohmann::json toJson(const GeometryContext &gctx, const Experimental::Portal &portal, const std::vector<const Experimental::DetectorVolume*> &detectorVolumes, const Options &options = Options{})
Convert to json format.
- Parameters
gctx – the geometry context
portal – the portal instance
detectorVolumes – is the list of all detector voluems for portal pointing
options – how to write this thing out
- Returns
a json object
-
std::vector<nlohmann::json> toJsonDetray(const GeometryContext &gctx, const Experimental::Portal &portal, std::size_t ip, const Experimental::DetectorVolume &volume, const OrientedSurfaces &orientedSurfaces, const std::vector<const Experimental::DetectorVolume*> &detectorVolumes, const Options &options = Options{})
Convert to json format - dedicated Detray function.
Note
that detray relies on singly connected masks, hence a portal from ACTS with multi volume link needs to be split into the multiple volumes
Note
detray also only has outside pointing links
- Parameters
gctx – the geometry context
portal – the portal instance
ip – is the portal index that could be used to pick the oriented surface
volume – is the detector volume to which these surfaces belong to
orientedSurfaces – are the bounding surfaces (may still need to be split)
detectorVolumes – is the list of all detector voluems for portal pointing
options – how to write this thing out
- Returns
a json object
-
struct Options
- #include <Acts/Plugins/Json/PortalJsonConverter.hpp>
Public Members
-
SurfaceJsonConverter::Options surfaceOptions = SurfaceJsonConverter::Options{}
Options how to write the surface out.
-
SurfaceJsonConverter::Options surfaceOptions = SurfaceJsonConverter::Options{}
-
namespace SurfaceBoundsJsonConverter
Functions
Conversion to surfaceBounds from json.
The type is given as a template argument in order to be able to construct the correct fitting types for surfaces.
- Parameters
j – the read-in json object
- Returns
a shared_ptr to a surface object for type polymorphism
-
nlohmann::json toJson(const SurfaceBounds &bounds)
Interface with detray conversion option.
- Parameters
bounds – is the bounds object
- Returns
the json object
-
nlohmann::json toJsonDetray(const SurfaceBounds &bounds, bool portal = false)
Interface with detray conversion option.
Note
reading back detray json format to Acts is not supported
- Parameters
bounds – is the bounds object
portal – is the flag for conversion into detray portal format
- Returns
the json object
-
namespace SurfaceJsonConverter
Functions
-
std::shared_ptr<Surface> fromJson(const nlohmann::json &jSurface)
The Surface converter from json.
- Parameters
jSurface – the surface json object
- Returns
a shared object created from json input
-
nlohmann::json toJson(const GeometryContext &gctx, const Surface &surface, const Options &options = Options{})
Contextual conversion of a surface.
- Parameters
gctx – the geometry context for this
surface – the surface to be converted
options – the writing options for the surfaces
- Returns
a json object representing the surface
-
nlohmann::json toJsonDetray(const GeometryContext &gctx, const Surface &surface, const Options &options = Options{})
Contextual conversion of a surface - Detray export.
Note
reading back detray json is not supported and will fail
- Parameters
gctx – the geometry context for this
surface – the surface to be converted
options – the writing options for the surfaces
- Returns
a json object representing the surface
-
struct Options
- #include <Acts/Plugins/Json/SurfaceJsonConverter.hpp>
Public Members
-
bool portal = false
-
Transform3JsonConverter::Options transformOptions = Transform3JsonConverter::Options{}
-
bool writeMaterial = true
-
bool portal = false
-
std::shared_ptr<Surface> fromJson(const nlohmann::json &jSurface)
-
namespace Test
-
namespace Transform3JsonConverter
Functions
-
Transform3 fromJson(const nlohmann::json &jTransform)
The Transform converter from json.
- Parameters
jTransform – the transform json transformation
- Returns
a transform object
-
nlohmann::json toJson(const Transform3 &t, const Options &options = {})
The Transform converter to json.
- Parameters
t – the transform to be converted
options – transformation options
- Returns
a json object representing the transform
-
struct Options
- #include <Acts/Plugins/Json/AlgebraJsonConverter.hpp>
The options for the transform converter.
Public Members
-
bool transpose = true
Apply a transpose to flip column/row order.
-
bool writeIdentity = false
Write the identity transform explicitly.
-
bool transpose = true
-
Transform3 fromJson(const nlohmann::json &jTransform)
-
namespace UnitConstants
All physical quantities have both a numerical value and a unit. For the computations we always choose a particular unit for a given physical quantity so we only need to consider the numerical values as such. The chosen base unit for a particular physical dimension, e.g. length, time, or energy, within this code base is called the native unit. The base units should be chosen such that they are internally consistent, require the least amount of explicit conversion factors (ideally none at all), and have typical numerical values close to unity to reduce numerical issues.
Here, the following native units are used:
Length is expressed in mm.
Time is expressed in [speed-of-light * time] == mm. A consequence of this choice is that the speed-of-light expressed in native units is 1.
Angles are expressed in radian.
Energy, mass, and momentum are all expressed in GeV (consistent with speed-of-light == 1).
Electric charge is expressed in e, i.e. units of the elementary charge.
The magnetic field is expressed in GeV/(e*mm). The magnetic field connects momentum to length, e.g. in SI units the radius of a charged particle trajectory in a constant magnetic field is given by
\[radius = - (momentum / charge) / field\]With the chosen magnetic field unit the expression above stays the same and no additional conversion factors are necessary.
Amount of substance is expressed in mol.
Depending on the context a physical quantity might not be given in the native units. In this case we need to convert to the native unit first before the value can be used. The necessary conversion factors are defined in
Acts::UnitConstants. Multiplying a value with the unit constant produces the equivalent value in the native unit, e.g.double length = 1 * Acts::UnitConstants::m; // length == 1000.0 double momentum = 100 * Acts::UnitConstants::MeV; // momentum == 0.1
The conversion of a value in native units into the equivalent value in a specific other unit is computed by dividing with the relevant unit, e.g.
double length = 10.0; // native units mm double lengthInM = length / Acts::UnitConstants::m; // == 0.01;
To further simplify the usage, physical quantities can also be expressed via C++ user literals defined in
Acts::UnitLiterals. This allows us to express quantities in a concise way:using namespace Acts::UnitLiterals; double length = 1_m; // == 1000.0 double momentum = 1.25_TeV; // == 1250.0 double lengthInUm = length / 1_um; // == 1000000.0 double momentumInMeV = momentum / 1_MeV; // == 1250000.0
To ensure consistent computations and results the following guidelines must be followed when handling physical quantities with units:
All unqualified numerical values, i.e. without a unit, are assumed to be expressed in the relevant native unit, e.g. mm for lengths or GeV for energy/momentum.
If a variable stores a physical quantity in a specific unit that is not the native unit, clearly mark this in the variable, i.e.
double momentum = 100.0; // momentum is stored as native unit GeV double momentumInMeV = 10.0; // would be 0.01 in native units
All input values must be given as
numerical_value * unit_constantor equivalently using the unit literals asvalue_unit. The resulting unqualified numerical value will be automatically converted to the native unit.To output an unqualified numerical value in the native units as a numerical value in a specific unit divide by the unit constants as
numerical_value / unit_constantor using the unit literals asvalue / 1_unit.
Examples:
#include <Acts/include/Definitions/Units.hpp> using namespace Acts::UnitLiterals; // define input values w/ units (via unit constants) double width = 12 * Acts::UnitConstants::mm; double mmuon = 105.7 * Acts::UnitConstants::MeV; // define input values w/ units (via unit user literals) double length = 23_cm; double time = 1214.2_ns; double angle = 123_degree; double momentum = 2.5_TeV; double mass = 511_keV; double velocity = 345_m / 1_s; double bfield = 3.9_T; // convert output values (via unit constants) double t_in_ns = trackPars.time() / Acts::UnitConstants::ns; // convert output values (via unit user literals) double x_in_mm = trackPars.position()[ePos0] / 1_mm; double p_in_TeV = trackPars.absoluteMomentum() / 1_TeV;
Note
A helper script is available in
Core/scripts/print_units_physical_constants.pyto validate some of the numerical values.Warning
Since using user-defined literals requires a namespace import of
Acts::UnitLiteralsit should not be used in headers since it would (accidentally) modify the namespace wherever the header is included.Variables
-
constexpr double cm = 1e1 * mm
-
constexpr double degree = 0.017453292519943295
-
constexpr double e = 1.0
Charge, native unit e (elementary charge)
-
constexpr double eV = 1e-9 * GeV
-
constexpr double fm = 1e-12 * mm
-
constexpr double fs = 1e-15 * s
-
constexpr double g = 1.0 / 1.782662e-24
-
constexpr double Gauss = 1e-4 * T
-
constexpr double GeV = 1.0
-
constexpr double h = 3600.0 * s
-
constexpr double J = 6241509074.460763 * GeV
-
constexpr double keV = 1e-6 * GeV
-
constexpr double kg = 1.0 / 1.782662e-27
-
constexpr double kGauss = 1e-1 * T
-
constexpr double km = 1e6 * mm
-
constexpr double m = 1e3 * mm
-
constexpr double MeV = 1e-3 * GeV
-
constexpr double min = 60.0 * s
-
constexpr double mm = 1.0
-
constexpr double mol = 1.0
Amount of substance, native unit mol.
-
constexpr double mrad = 1e-3
-
constexpr double ms = 1e-3 * s
-
constexpr double nm = 1e-6 * mm
-
constexpr double ns = 1e-9 * s
-
constexpr double pm = 1e-9 * mm
-
constexpr double ps = 1e-12 * s
-
constexpr double rad = 1.0
-
constexpr double s = 299792458000.0
Note
Depends on speed of light in SI units
-
constexpr double T = 0.000299792458
Magnetic field, native unit (eV*s)/(e*m²)
Note
Depends on speed of light in SI units
-
constexpr double TeV = 1e3 * GeV
-
constexpr double u = 0.93149410242
atomic mass unit u
-
constexpr double um = 1e-3 * mm
-
constexpr double us = 1e-6 * s
-
namespace UnitLiterals
-
namespace VectorHelpers
Functions
-
inline double cast(const Vector3 &position, BinningValue bval)
Helper method to extract the binning value from a 3D vector.
For this method a 3D vector is required to guarantee all potential binning values.
-
inline ActsMatrix<3, 3> cross(const ActsMatrix<3, 3> &m, const Vector3 &v)
Calculates column-wise cross products of a matrix and a vector and stores the result column-wise in a matrix.
- Parameters
m – [in] Matrix that will be used for cross products
v – [in] Vector for cross products
- Returns
Constructed matrix
-
template<typename Derived>
double eta(const Eigen::MatrixBase<Derived> &v) noexcept Calculate the pseudorapidity for a vector.
Note
Will static assert that the number of rows of
vis at least 3, or in case of dynamic size, will abort execution if that is not the case.- Template Parameters
Derived – Eigen derived concrete type
- Parameters
v – Any vector like Eigen type, static or dynamic
- Returns
The pseudorapidity value
-
inline std::array<ActsScalar, 5> evaluateTrigonomics(const Vector3 &direction)
Fast evaluation of trigonomic functions.
- Parameters
direction – for this evaluatoin
- Returns
cos(phi), sin(phi), cos(theta), sin(theta), 1/sin(theta)
-
template<typename vector3_t>
inline auto makeVector4(const Eigen::MatrixBase<vector3_t> &vec3, typename vector3_t::Scalar w) -> Eigen::Matrix<typename vector3_t::Scalar, 4, 1> Construct a four-vector from a three-vector and scalar fourth component.
-
template<typename Derived>
double perp(const Eigen::MatrixBase<Derived> &v) noexcept Calculate radius in the transverse (xy) plane of a vector.
Note
Will static assert that the number of rows of
vis at least 2, or in case of dynamic size, will abort execution if that is not the case.- Template Parameters
Derived – Eigen derived concrete type
- Parameters
v – Any vector like Eigen type, static or dynamic
- Returns
The transverse radius value.
-
template<typename Derived>
double phi(const Eigen::MatrixBase<Derived> &v) noexcept Calculate phi (transverse plane angle) from compatible Eigen types.
Note
Will static assert that the number of rows of
vis at least 2, or in case of dynamic size, will abort execution if that is not the case.- Template Parameters
Derived – Eigen derived concrete type
- Parameters
v – Any vector like Eigen type, static or dynamic
- Returns
The value of the angle in the transverse plane.
-
template<typename T, std::enable_if_t<detail::has_phi_method<T>::value, int> = 0>
double phi(const T &v) noexcept Calculate phi (transverse plane angle) from anything implementing a method like
phi()returning anything convertible todouble.- Template Parameters
T – anything that has a phi method
- Parameters
v – Any type that implements a phi method
- Returns
The phi value
-
inline auto position(const FreeVector ¶ms)
Access the three-position components in a free parameters vector.
-
inline auto position(const Vector4 &pos4)
Access the three-position components in a four-position vector.
-
template<typename Derived>
double theta(const Eigen::MatrixBase<Derived> &v) noexcept Calculate the theta angle (longitudinal w.r.t.
z axis) of a vector
Note
Will static assert that the number of rows of
vis at least 3, or in case of dynamic size, will abort execution if that is not the case.- Template Parameters
Derived – Eigen derived concrete type
- Parameters
v – Any vector like Eigen type, static or dynamic
- Returns
The theta value
-
inline double cast(const Vector3 &position, BinningValue bval)
-
namespace VolumeBoundsJsonConverter
Functions
-
template<typename bounds_t>
std::unique_ptr<bounds_t> fromJson(const nlohmann::json &jVolumeBounds) Conversion to volume bounds from json.
The type is given as a template argument in order to be able to construct the correct fitting types for surfaces.
- Parameters
jVolumeBounds – the read-in json object
jVolumeBounds – the read-in json object
- Returns
a unique_ptr to a volume bounds object for type polymorphism
- Returns
a unique_ptr to a volume bounds object for type polymorphism
-
nlohmann::json toJson(const VolumeBounds &bounds)
Conversion to Json from volume bounds.
- Parameters
bounds – is the bounds object
- Returns
the json object
-
template<typename bounds_t>
-
using ActsDynamicMatrix = Eigen::Matrix<ActsScalar, Eigen::Dynamic, Eigen::Dynamic>