Class Acts::TrapezoidBounds
-
class TrapezoidBounds : public Acts::PlanarBounds
Bounds for a trapezoidal, planar Surface.
Public Types
Public Functions
-
TrapezoidBounds() = delete
-
inline TrapezoidBounds(const std::array<double, eSize> &values) noexcept(false)
Constructor for symmetric Trapezoid - from fixed size array.
- Parameters
values – the values to be stream in
-
inline TrapezoidBounds(double halfXnegY, double halfXposY, double halfY) noexcept(false)
Constructor for symmetric Trapezoid.
- Parameters
halfXnegY – minimal half length X, definition at negative Y
halfXposY – maximal half length X, definition at positive Y
halfY – half length Y - defined at x=0
-
~TrapezoidBounds() override
-
virtual const RectangleBounds &boundingBox() const final
Bounding box parameters.
- Returns
rectangle bounds for a bounding box
-
inline double get(BoundValues bValue) const
Access to the bound values.
- Parameters
bValue – the class nested enum for the array access
-
virtual bool inside(const Vector2 &lposition, const BoundaryCheck &bcheck) const final
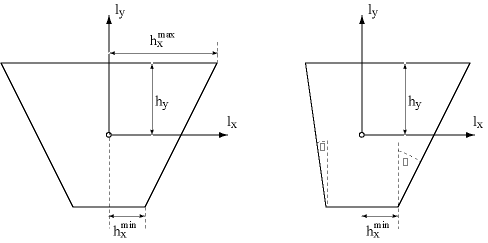
The orientation of the Trapezoid is according to the figure above, in words: the shorter of the two parallel sides of the trapezoid intersects with the negative \( y \) - axis of the local frame.
The cases are:
(0)
\( y \) or \( x \)bounds are 0 || 0
(1) the local position is outside
\( y \)bounds
(2) the local position is inside
\( y \) bounds, but outside maximum \( x \)bounds
(3) the local position is inside
\( y \) bounds AND inside minimum \( x \)bounds
(4) the local position is inside
\( y \) bounds AND inside maximum \( x \) bounds, so that it depends on the \( eta \) coordinate (5) the local position fails test of (4)The inside check is done using single equations of straight lines and one has to take care if a point lies on the positive \( x \) half area(I) or the negative one(II). Denoting \( |x_{min}| \) and \( | x_{max} | \) as
minHalfXrespectivelymaxHalfX, such as \( | y_{H} | \) ashalfY, the equations for the straing lines in (I) and (II) can be written as:(I): \( y = \kappa_{I} x + \delta_{I} \)
(II): \( y = \kappa_{II} x + \delta_{II} \)
,
where
\( \kappa_{I} = - \kappa_{II} = 2 \frac{y_{H}}{x_{max} - x_{min}} \) and \( \delta_{I} = \delta_{II} = - \frac{1}{2}\kappa_{I}(x_{max} + x_{min}) \)
- Parameters
lposition – Local position (assumed to be in right surface frame)
bcheck – boundary check directive
- Returns
boolean indicator for the success of this operation
-
virtual std::ostream &toStream(std::ostream &sl) const final
Output Method for std::ostream.
- Parameters
sl – is the ostream to be dumped into
-
virtual BoundsType type() const final
Return the bounds type - for persistency optimization.
- Returns
is a BoundsType enum
-
inline virtual std::vector<double> values() const final
Access method for bound values, this is a dynamically sized vector containing the parameters needed to describe these bounds.
- Returns
of the stored values for this SurfaceBounds object
-
TrapezoidBounds() = delete